
第四章 分解方法及单口网络 2018年10月
第四章 分解方法及单口网络 1 2018年10月
网络分解的目的 运用节点法或网孔法对复杂网络进行分析时,如果只 对其中某一支路的电压、电流或其中某些局部的电压、 电流感兴趣时,仍嫌联立方程太多。 解决这一问题的一种办法是把这个“大”网络分解为 若干个“小”网络,即若干个子网络,对这些子网络 逐一求解从而得出所需结果。 ?最简单的情况是把原网络看成是由两个通过两根导线 相连的子网络N,和N2所组成。 N N2 2
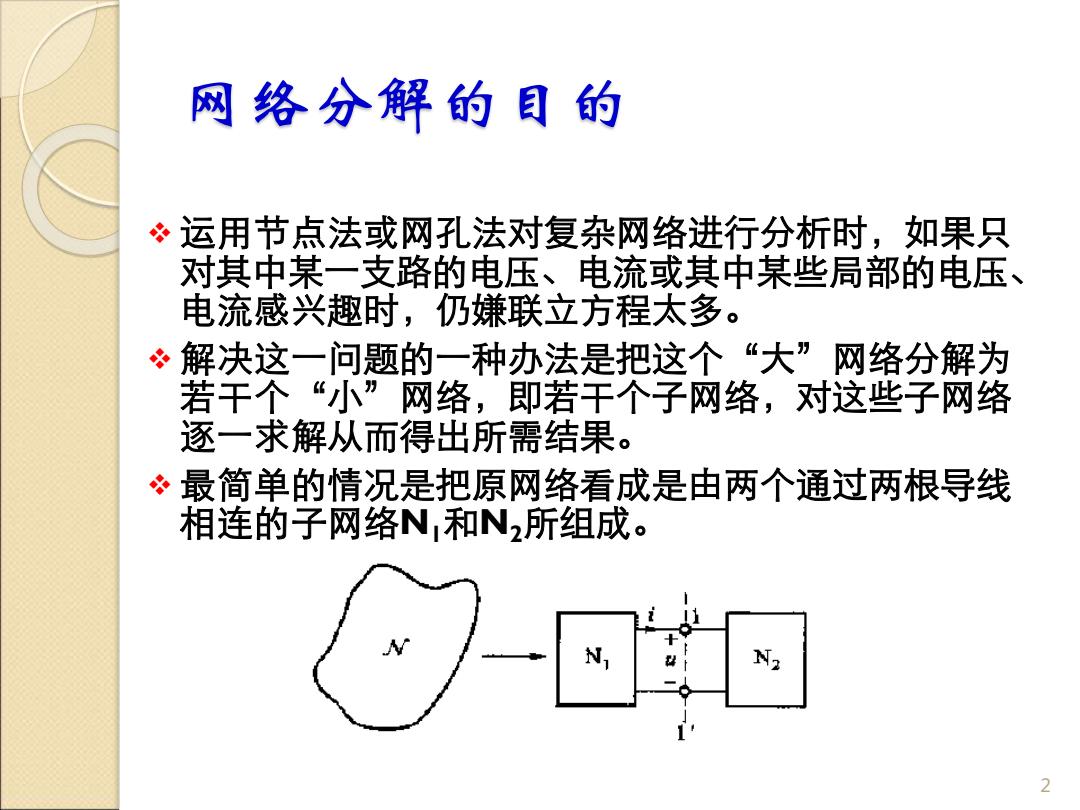
网络分解的目的 ❖ 运用节点法或网孔法对复杂网络进行分析时,如果只 对其中某一支路的电压、电流或其中某些局部的电压、 电流感兴趣时,仍嫌联立方程太多。 ❖ 解决这一问题的一种办法是把这个“大”网络分解为 若干个“小”网络,即若干个子网络,对这些子网络 逐一求解从而得出所需结果。 ❖ 最简单的情况是把原网络看成是由两个通过两根导线 相连的子网络N1和N2所组成。 2

单口网络 对外只有两个端钮的网络整体称为二端网络或单口 网络。 一个元件的电压电流关系是由元件本身所确定的, 与外接的电路无关;一个单口网络除了通过它的两 个端钮与外界相连接外,别无其他联系,则单口网 络的VAR也是由网络本身所确定的,与外接电路无 关。 当对一个网络N进行分解处理时,首先应把单口网 络N和N2从原网络中分离出来,求得它们的VAR, 然后再设法求得它们相连时的端口电压“和端口电流 i。 3
单口网络 ❖ 对外只有两个端钮的网络整体称为二端网络或单口 网络。 ❖ 一个元件的电压电流关系是由元件本身所确定的, 与外接的电路无关;一个单口网络除了通过它的两 个端钮与外界相连接外,别无其他联系,则单口网 络的VAR也是由网络本身所确定的,与外接电路无 关。 ❖ 当对一个网络N进行分解处理时,首先应把单口网 络N1和N2从原网络中分离出来,求得它们的VAR, 然后再设法求得它们相连时的端口电压u和端口电流 i。 3
§4-1分解的基本步骤 冬分解的基本步骤为: (I)把网络划分为两个单口网络N,和N2; (2)分别求出N,和N2的VAR(计算或测量); (3)联立两者的VAR式或由它们伏安特性曲线的交点, 求得N,和N2的端电压、电流; (4)分别求解N,和N2内部各支路电压、电流。 2 0 Ug/R 4
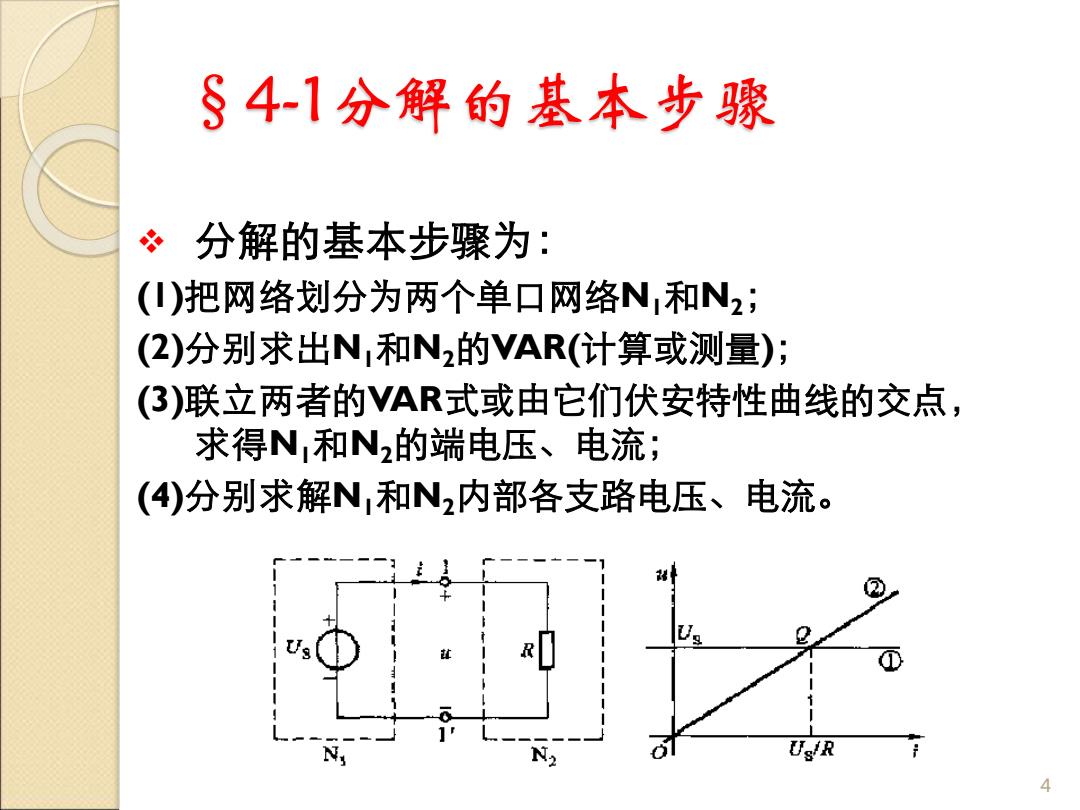
§4-1分解的基本步骤 ❖ 分解的基本步骤为: (1)把网络划分为两个单口网络N1和N2; (2)分别求出N1和N2的VAR(计算或测量); (3)联立两者的VAR式或由它们伏安特性曲线的交点, 求得N1和N2的端电压、电流; (4)分别求解N1和N2内部各支路电压、电流。 4

§4-2单口网络的电压电流关系 如果在单口网络中不含有任何能通过电或非电的方 式与网络之外的某些变量相耦合的元件,则这单口 网络称为明确的。 单口可以用下列的几种方式之一来描述: ) 详尽的电路模型; 2) 端口电压与电流的约束关系:方程或曲线; 3) 等效电路。 其中以2)最具表征意义,相当于元件的约束关系, 当单口内部情况不明时,可以用实验方法测得。 5
§4-2 单口网络的电压电流关系 ❖ 如果在单口网络中不含有任何能通过电或非电的方 式与网络之外的某些变量相耦合的元件,则这单口 网络称为明确的。 ❖ 单口可以用下列的几种方式之一来描述: 1) 详尽的电路模型; 2) 端口电压与电流的约束关系:方程或曲线; 3) 等效电路。 ❖ 其中以2)最具表征意义,相当于元件的约束关系, 当单口内部情况不明时,可以用实验方法测得。 5
例4-1 试求含电压源和电阻的单口网络 的VAR。 10V( 20 解单口网络的VAR是由它本身 性质决定的,与外接电路无关。 因此,可以在任何外接电路X的 10=5i1+w 情况下来求它的VAR。 u=20(i1-i) 先列出整个电路的方程,然后消 去除u和以外的所有变量。 消去1 u=8-4i 6
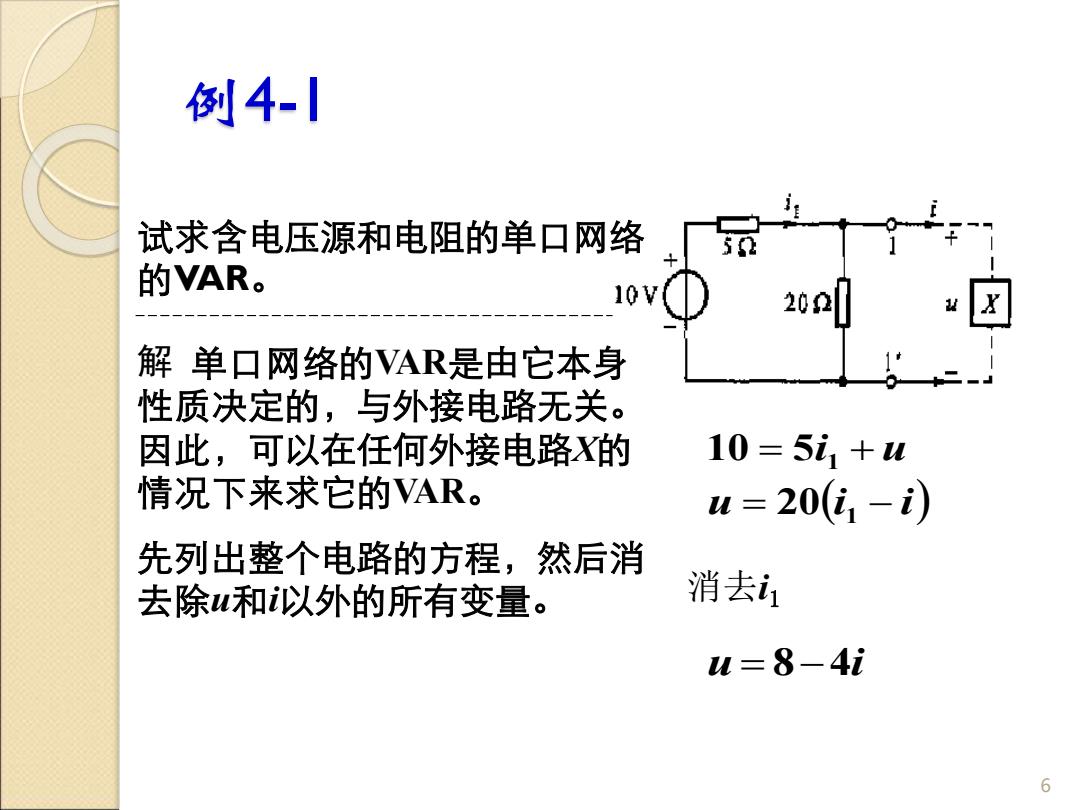
例4-1 试求含电压源和电阻的单口网络 的VAR。 6 解 单口网络的VAR是由它本身 性质决定的,与外接电路无关。 因此,可以在任何外接电路X的 情况下来求它的VAR。 先列出整个电路的方程,然后消 去除u和i以外的所有变量。 消去i1 u (i i) i u = − = + 1 1 20 10 5 u = 8−4i

X为电流源 ÷如果设想X是一个电流源1 (设方向向下),且设其两端 电压为u(设正极在上),则 10V 202 由节点法可以更方便可求得 结果。 ?该电路共有两个节点电压 其一即为电流源两端的电压 u,亦即单口网络的端口电 压;另一为已知电压源的电 压,其值为IOV,故得节点 i=i, 电压方程: w=8-4i 7
X为电流源 ❖ 如果设想X是一个电流源 i s (设方向向下 ),且设其两端 电压为 u (设正极在上 ),则 由节点法可以更方便可求得 结果。 ❖ 该电路共有两个节点电压, 其一即为电流源两端的电压 u,亦即单口网络的端口电 压;另一为已知电压源的电 压,其值为10 V,故得节点 电压方程: 7 u i i i u i s s 8 4 10 51 201 51= − = = − − +
X为电压源 ÷用“外施电压源求电流”的方法来解决求VAR的 问题。 ÷可设想X为电压源,此电压源的电压显然即为单口 网络的端口电压u,所求的电流显然即为单口网络 的端口电流i。 冬如用节点法,则方程当为 202 u=8-4i 8
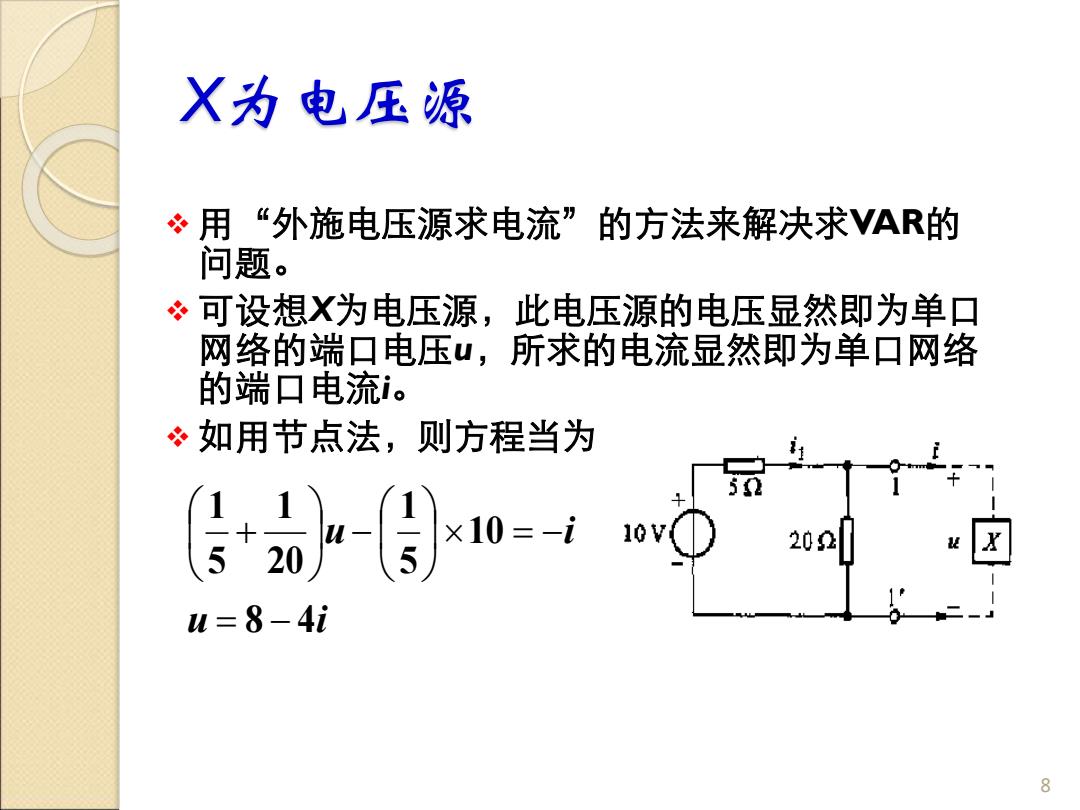
X为电压源 ❖ 用“外施电压源求电流”的方法来解决求VAR的 问题。 ❖ 可设想X为电压源,此电压源的电压显然即为单口 网络的端口电压u,所求的电流显然即为单口网络 的端口电流i。 ❖ 如用节点法,则方程当为 8 u i u i 8 4 10 5 1 20 1 5 1 = − = − − +

结论 单口网络的VAR与外接电路无关,因此,完全可以在 最简单的外接电路情况下,求得它的VAR。 ?外施电流源求电压法和外施电压源求电流法是常用的 方法,也是用实验方法确定VAR的依据。 9
结论 ❖ 单口网络的VAR与外接电路无关,因此,完全可以在 最简单的外接电路情况下,求得它的VAR。 ❖ 外施电流源求电压法和外施电压源求电流法是常用的 方法,也是用实验方法确定VAR的依据。 9
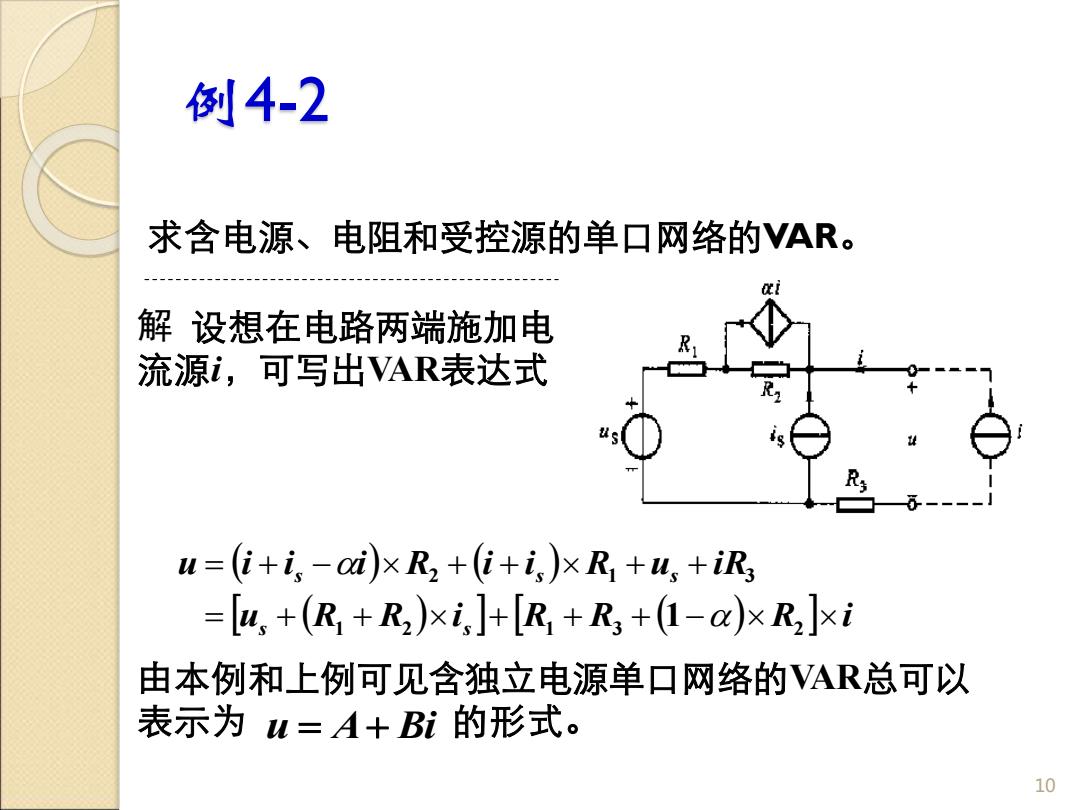
例4-2 求含电源、电阻和受控源的单口网络的VAR。 解设想在电路两端施加电 流源i,可写出VAR表达式 u=(i+i,-ai)xR2+(i+is)xR+u,+iRs =[w+(R+R2)xi,]+[R+R3+(1-a)xR2]xi 由本例和上例可见含独立电源单口网络的VAR总可以 表示为M=A+Bi的形式。 10
例4-2 求含电源、电阻和受控源的单口网络的VAR。 10 解 设想在电路两端施加电 流源i,可写出VAR表达式 由本例和上例可见含独立电源单口网络的VAR总可以 表示为 u = A+ Bi 的形式。 ( ) ( ) u (R R ) i R R ( ) R i u i i i R i i R u i R s s s s s = + + + + + − = + − + + + + 1 2 1 3 2 2 1 3 1