
第二章 运用独立电流、电压变 量的分析方法 2018年9月17日 1
第二章 运用独立电流、电压变 量的分析方法 1 2018年9月17日

§2-|网孔分析法 在n个节点的电路中,b个支路电流是用(n-)个KCL 方程联系的,因而给定[b-(n-)门个电流即能确定余 下的(n-)个电流。 第一步求解的对象必须为[b-(n-)门个独立电流变量。 第二步用KCL解决的(n-)个电流,使问题得到完全 解决。 使用的网孔电流可以得到一组完备的独立电流变量。 2
§2-1网孔分析法 ❖ 在n个节点的电路中, b个支路电流是用(n-1)个KCL 方程联系的,因而给定[b-(n-1)]个电流即能确定余 下的(n-1)个电流。 ❖ 第一步求解的对象必须为[b-(n-1)]个独立电流变量。 ❖ 第二步用KCL解决的(n-1)个电流,使问题得到完全 解决。 ❖ 使用的网孔电流可以得到一组完备的独立电流变量。 2
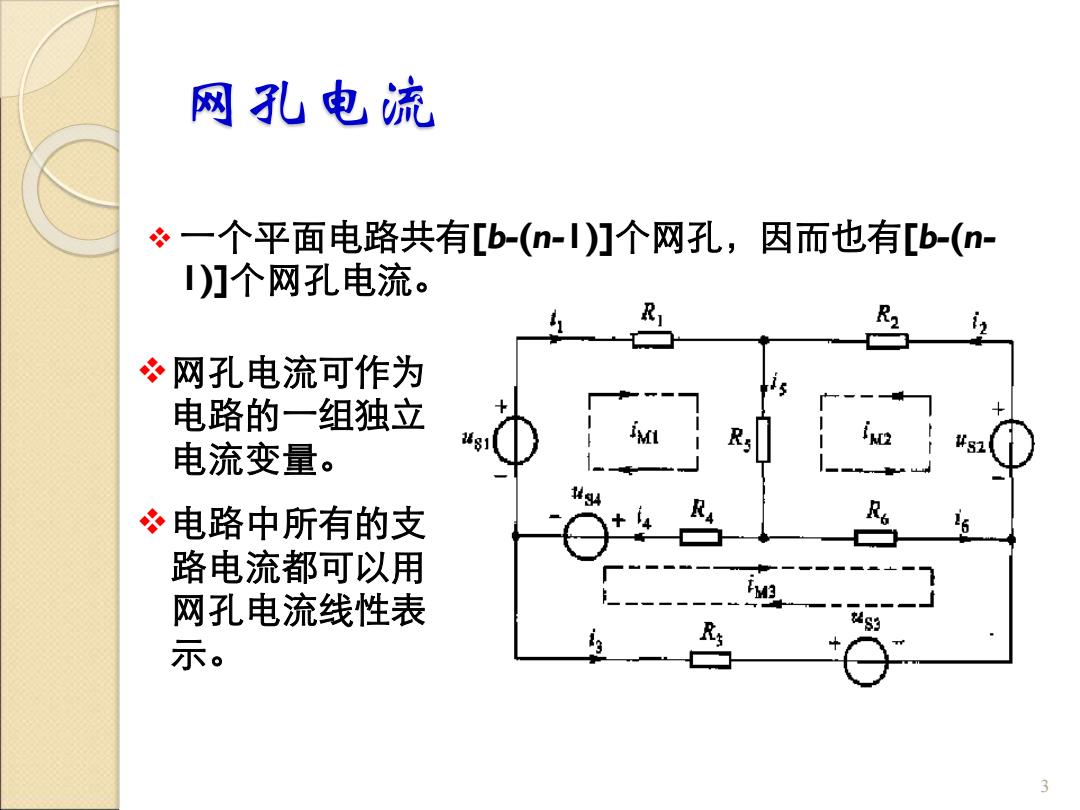
网孔电流 冬一个平面电路共有[b-(n-)门个网孔,因而也有[b-(n- )门个网孔电流。 冬网孔电流可作为 电路的一组独立 电流变量。 1 必电路中所有的支 路电流都可以用 网孔电流线性表 示。 3 3
网孔电流 ❖ 一个平面电路共有[b-(n-1)]个网孔,因而也有[b-(n- 1)]个网孔电流。 3 ❖网孔电流可作为 电路的一组独立 电流变量。 ❖电路中所有的支 路电流都可以用 网孔电流线性表 示

网孔方程 网孔电流不能用KCL相联系,但能根据KVL及支路 VAR为每一个网孔列写一个KVL方程,方程中的支路 电压可以通过欧姆定律用网孔电流来表示。 R1W1+R,(i1+iw2)+R(iM1-ig3)+u54-us1=0 R2iw2+R,(iw2+iui)+R,(i2+iwa)-u2=0 R313+R(iW3-iWi)+R(i3+iw2)-us4-us3=0 整理得 R +R+Rs )im+Rsim2-Rain3=ust-uss Rsin+(R+Rs+Ro)imz+Rciv3 =us? -Ryimi+Roimz +(R3 +Rs+R6)iM3=us3+us4 4
网孔方程 ❖ 网孔电流不能用KCL相联系,但能根据KVL及支路 VAR为每一个网孔列写一个KVL方程,方程中的支路 电压可以通过欧姆定律用网孔电流来表示。 4 整理得 + − + + − − = + + + + − = + + + − + − = ( ) ( ) 0 ( ) ( ) 0 ( ) ( ) 0 3 3 4 3 1 6 3 2 4 3 2 2 5 2 1 6 2 3 2 1 1 5 1 2 4 1 3 4 1 M M M M M S S M M M M M S M M M M M S S R i R i i R i i u u R i R i i R i i u R i R i i R i i u u ( ) ( ) ( ) − + + + + = + + + + + = + + + − = − 4 1 6 2 3 4 6 3 3 4 5 1 2 5 6 2 6 3 2 1 4 5 1 5 2 4 3 1 4 M M M S S M M M S M M M S S R i R i R R R i u u R i R R R i R i u R R R i R i R i u u

网孔方程一般表达式 RuiMi+Rizim2+Ri3iv3 usu Rimi+Rzzivz +Rzim3 =us22 Rsim+R3zim2+R3sim3 =us33 ÷R1、R22、R3分别称为网孔I、网孔2和网孔3的自电 阻。它们分别是各自网孔内所有电阻的总和。 ÷R2称为网孔I与网孔2的互电阻。它是该两网孔的公 有电阻,即R12=R5 R13称为网孔I与网孔3的互电阻,取负值,即R13=-R4 因为M和M3以相反的方向流过公有电阻R4 ”其他电阻类推。 u、u22和u33分别为网孔I、网孔2、网孔3中各电 压源电压升的代数和。 5
网孔方程一般表达式 ❖ R11、R22、R33分别称为网孔1、网孔2和网孔3的自电 阻。它们分别是各自网孔内所有电阻的总和。 ❖ R12称为网孔1与网孔2的互电阻。它是该两网孔的公 有电阻,即R12=R5。 ❖ R13称为网孔1与网孔3的互电阻,取负值,即R13=-R4。 因为iM1和iM3以相反的方向流过公有电阻R4。 ❖ 其他电阻类推。 ❖ us11、us22和us33分别为网孔1、网孔2、网孔3中各电 压源电压升的代数和。 5 + + = + + = + + = 31 1 32 2 33 3 33 21 1 22 2 23 3 22 11 1 12 2 13 3 11 M M M S M M M S M M M S R i R i R i u R i R i R i u R i R i R i u

个网孔的电路网孔方程 冬具有个网孔的电路,网孔方程的形式应为: Riini+Rizimz+..+Rimivm =us1 Rzimi+R22iy2+.+R2mimm us22 Rmim+Rm2im2++Romimm =us33 6
m个网孔的电路网孔方程 ❖具有m个网孔的电路,网孔方程的形式应为: 6 + + + = + + + = + + + = 1 1 2 2 3 3 2 1 1 2 2 2 2 2 2 1 1 1 1 2 2 1 1 1 ... ...... ... ... m M m M mm Mm S M M m Mm S M M m Mm S R i R i R i u R i R i R i u R i R i R i u
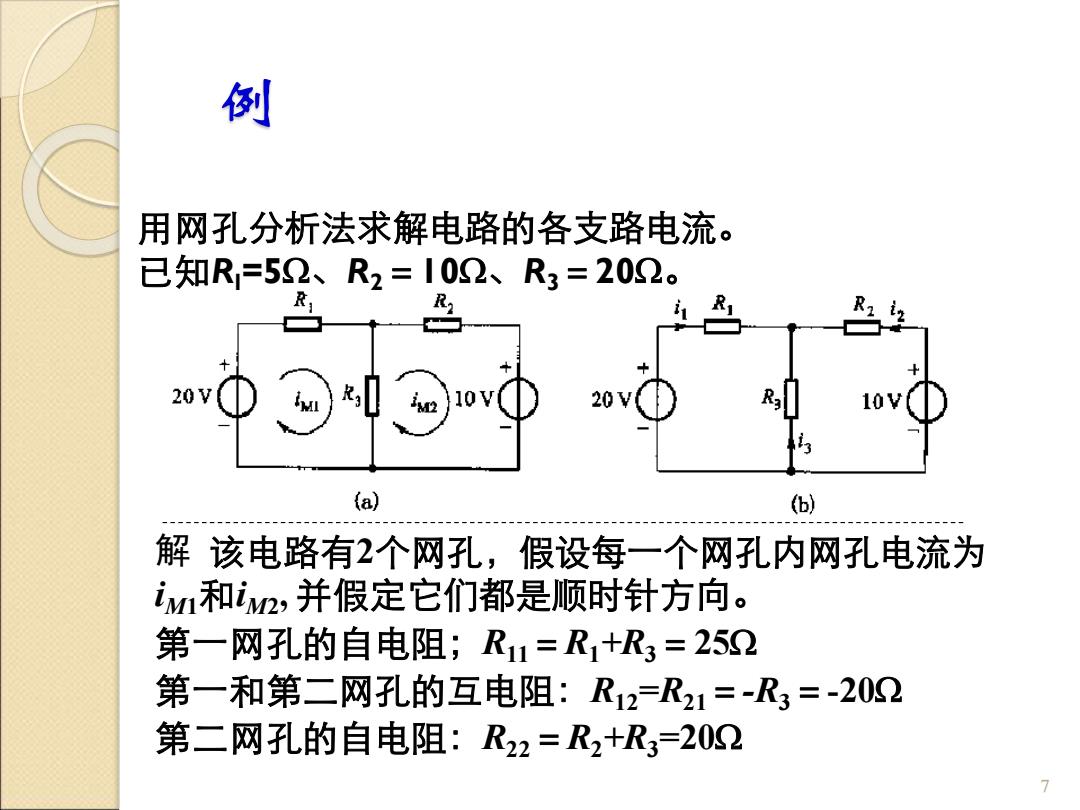
例 用网孔分析法求解电路的各支路电流。 已知R=52、R2=102、R3=202。 R 20V 20 (a) (b) 解该电路有2个网孔,假设每一个网孔内网孔电流为 iM和iM2,并假定它们都是顺时针方向。 第一网孔的自电阻;R1=R1+R3=252 第一和第二网孔的互电阻:R12=R21=-R3=-202 第二网孔的自电阻:R22=R2+R3=202 7
例 用网孔分析法求解电路的各支路电流。 已知Rl=5、R2=10、R3=20。 7 解 该电路有2个网孔,假设每一个网孔内网孔电流为 iM1和iM2 , 并假定它们都是顺时针方向。 第一网孔的自电阻;R11=R1+R3=25 第一和第二网孔的互电阻:R12=R21=-R3=-20 第二网孔的自电阻:R22=R2+R3=20

解答 电源(升压为正,降压为负): Ws11=20V us22=-10V 网孔方程为: 25iM1-20iM2=20 -20iM1+30iM2=-10 各支路电流: i=im iz =-iv2 is =im2-imi 8
解答 电源(升压为正,降压为负): 8 网孔方程为: 各支路电流: 3 2 1 2 2 1 1 1 2 1 2 2 2 1 1 20 30 10 25 20 20 10 20 M M M M M M M M S S i i i i i i i i i i i u V u V = − = − = − + = − − = = − =
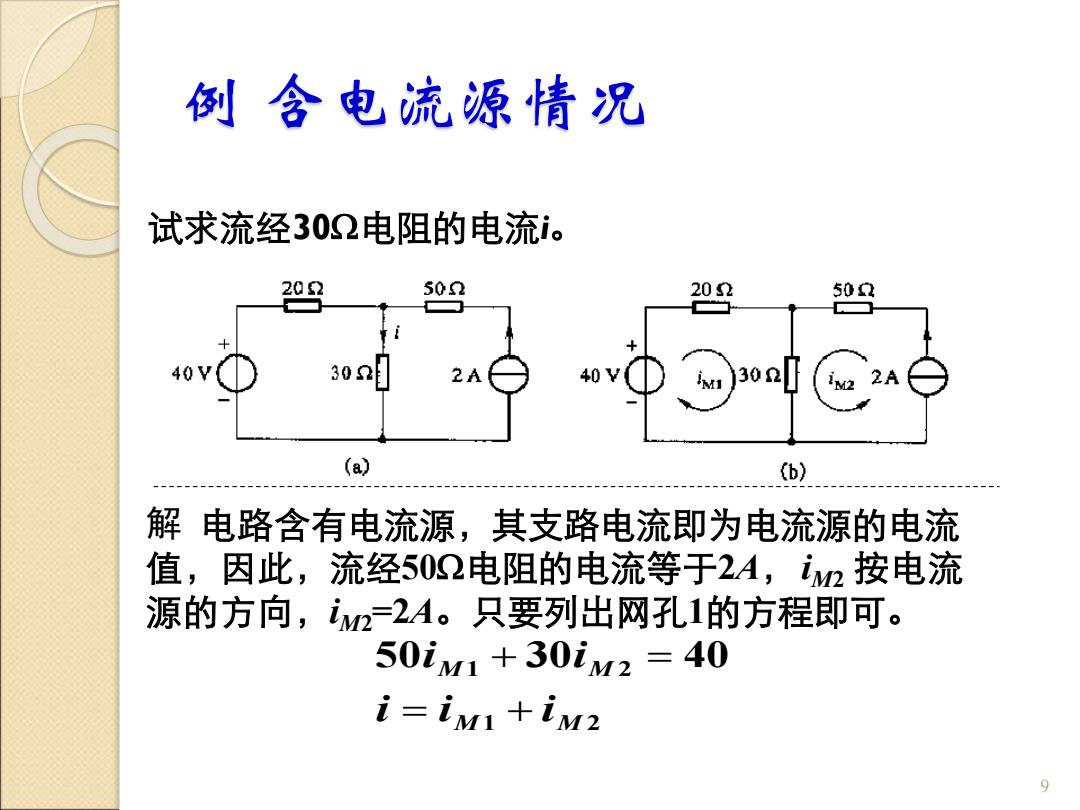
例含电流源情况 试求流经302电阻的电流i。 202 50 202 502 302 2A (a) (b) 解电路含有电流源,其支路电流即为电流源的电流 值,因此,流经502电阻的电流等于2A,iM2按电流 源的方向,iw22A。只要列出网孔1的方程即可。 50iM1+30iM2=40 i=ini+im2 9
例 含电流源情况 试求流经30电阻的电流i。 9 解 电路含有电流源,其支路电流即为电流源的电流 值,因此,流经50电阻的电流等于2A,iM2 按电流 源的方向,iM2=2A。只要列出网孔1的方程即可。 1 2 50 1 30 2 40 M M M M i i i i i = + + =
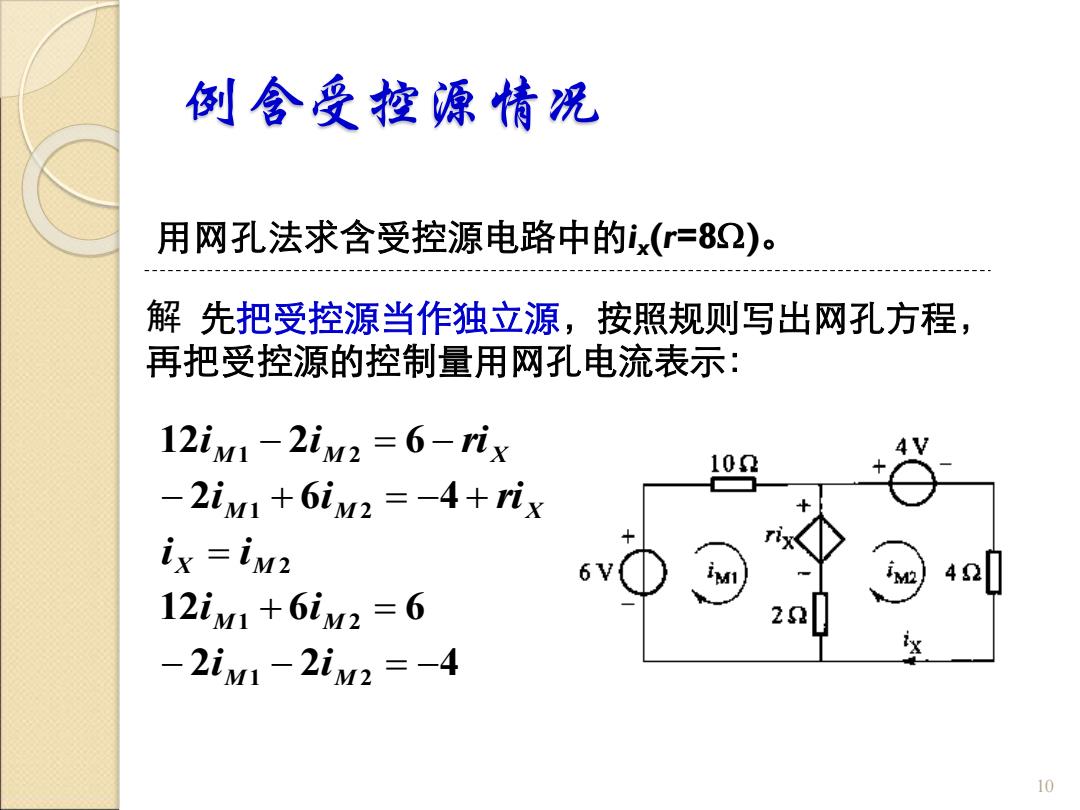
例含受控源情况 用网孔法求含受控源电路中的ix(=82)。 解先把受控源当作独立源,按照规则写出网孔方程, 再把受控源的控制量用网孔电流表示: 12iM1-2iM2=6-ix 10 -2iM1+6iM2=-4+ix ix =im2 12iw1+6iM2=6 -2iM1-2iM2=-4 10
例含受控源情况 用网孔法求含受控源电路中的ix (r=8)。 10 解 先把受控源当作独立源,按照规则写出网孔方程, 再把受控源的控制量用网孔电流表示: 2 2 4 12 6 6 2 6 4 12 2 6 1 2 1 2 2 1 2 1 2 − − = − + = = − + = − + − = − M M M M X M M M X M M X i i i i i i i i ri i i ri