
交流动态电路 1
交流动态电路 1

交流电路 如果电路中所含的电源是交流电源,则称该电路为 交流电路。交流电压源的电压以及交流电流源的电 流都是随时间作周期性的变化的,如果这一变化方 式按正弦规律变化,则称为正弦交流电源。 如果交流电路中除电源外所含的元件至少有一个是 动态元件,则称该电路为交流动态电路。 ÷电力供电系统可用交流动态电路作为模型。通信及 自动控制电路中的周期信号一般虽然不是按正弦方 式变化的,但通过博里叶级数可把信号分解为无限 多项与频率成整数倍的正弦信号之和,在一定条件 下仍可按交流动态电路处理。 2
交流电路 ❖ 如果电路中所含的电源是交流电源,则称该电路为 交流电路。交流电压源的电压以及交流电流源的电 流都是随时间作周期性的变化的,如果这一变化方 式按正弦规律变化,则称为正弦交流电源。 ❖ 如果交流电路中除电源外所含的元件至少有一个是 动态元件,则称该电路为交流动态电路。 ❖ 电力供电系统可用交流动态电路作为模型。通信及 自动控制电路中的周期信号一般虽然不是按正弦方 式变化的,但通过博里叶级数可把信号分解为无限 多项与频率成整数倍的正弦信号之和,在一定条件 下仍可按交流动态电路处理。 2
§.1周期电压和电流 随时间变化的电压和电流称为时变电压和电流,如 果给出参考方向,在任一时刻t,电压或电流的数值 便可由函数u(t)或(t)确定。 时变电压和电流在任一时刻的数值,称为它们的瞬 时值。 必 根据电压或电流瞬时值的正负号结合参考方向,可 确定电压降或电流的真实方向。电压u的双下标即表 明电压降的参考方向。 ia) (b)
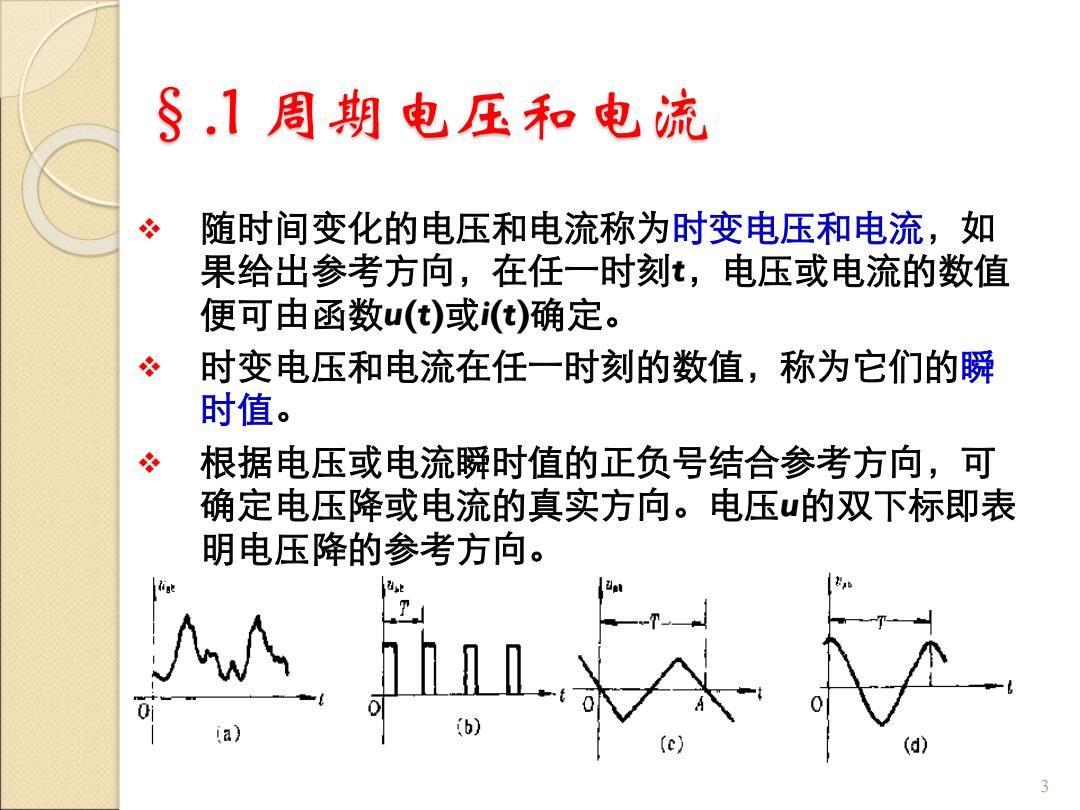
§.1 周期电压和电流 ❖ 随时间变化的电压和电流称为时变电压和电流,如 果给出参考方向,在任一时刻t,电压或电流的数值 便可由函数u(t)或i(t)确定。 ❖ 时变电压和电流在任一时刻的数值,称为它们的瞬 时值。 ❖ 根据电压或电流瞬时值的正负号结合参考方向,可 确定电压降或电流的真实方向。电压u的双下标即表 明电压降的参考方向。 3

周期电压和周期电流 ?如果时变电压和电流的每个值在经过相等的时间后重 复出现,这种时变的电压和电流是周期性的,称为周 期电压和周期电流。周期电压应满足: t=t+kT) k为任何整数。称为周期,它是波形再次重复出现 所需的最短时间间隔,单位为秒。 单位时间内的循环(周期)数称为频率。以「表示频率, 显然 f= 频率的单位为赫兹(赫或Hz)。 4
周期电压和周期电流 ❖ 如果时变电压和电流的每个值在经过相等的时间后重 复出现,这种时变的电压和电流是周期性的,称为周 期电压和周期电流。周期电压应满足: k为任何整数。T称为周期,它是波形再次重复出现 所需的最短时间间隔,单位为秒。 ❖ 单位时间内的循环(周期)数称为频率。以 f 表示频率, 显然 频率的单位为赫兹(赫或Hz)。 4 u(t) = u(t + kT) T f 1 =
§,2正孩电压和电流 ?随时间按正弦规律变化的电压和电流称为正弦电压和 正弦电流,正弦波是周期波形的基本形式。 正弦规律即简谐规律,可用时间的sin函数表示,也 可用时间的cos函数表示。本书采用cos函数。 u(t)=U cosot 其中Um为电压的振幅,它是一个常量,t是一个随 时间变化的角度,⊙侧是一个与频率有关的常量。为 角频率,单位为弧度/秒。 2π 2 T 4 (s) 3 2x ot (rad) 2 2 2 5
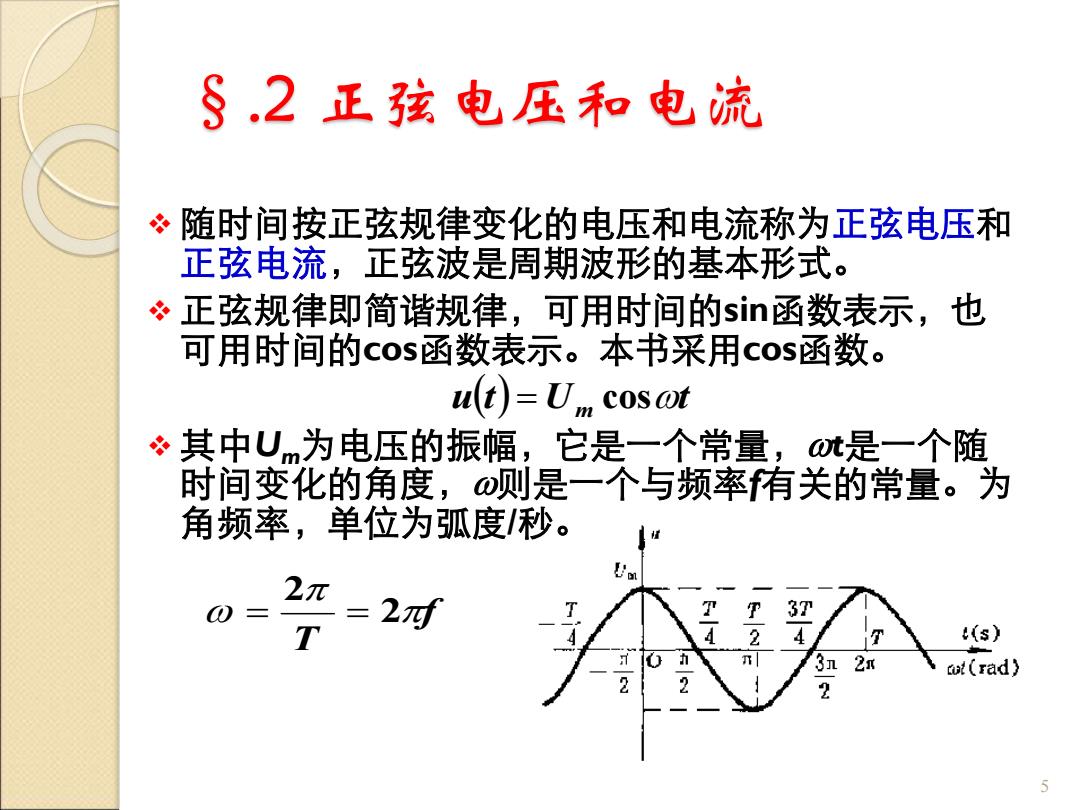
§.2 正弦电压和电流 ❖ 随时间按正弦规律变化的电压和电流称为正弦电压和 正弦电流,正弦波是周期波形的基本形式。 ❖ 正弦规律即简谐规律,可用时间的sin函数表示,也 可用时间的cos函数表示。本书采用cos函数。 ❖ 其中Um为电压的振幅,它是一个常量,t是一个随 时间变化的角度,则是一个与频率f有关的常量。为 角频率,单位为弧度/秒。 5 u(t) U t = m cos f T 2 2 = =
初相角 在一般情况下,时间的起点不一定恰好选在正弦波为 正最大值的瞬间。 冬以角度来计量,时间起点选在离正弦波正最大值瞬间 之后角处,即当t=-时,才有u=Um。因此,该 正弦电压应表示为 u(t)=U cos(ot+0) 称为初相角,简称初相。它反映了正弦波初始值的 大小,即 u(0)=U,cos(0) 初相角用弧度为单位, 2 但在工程上常用度。 6
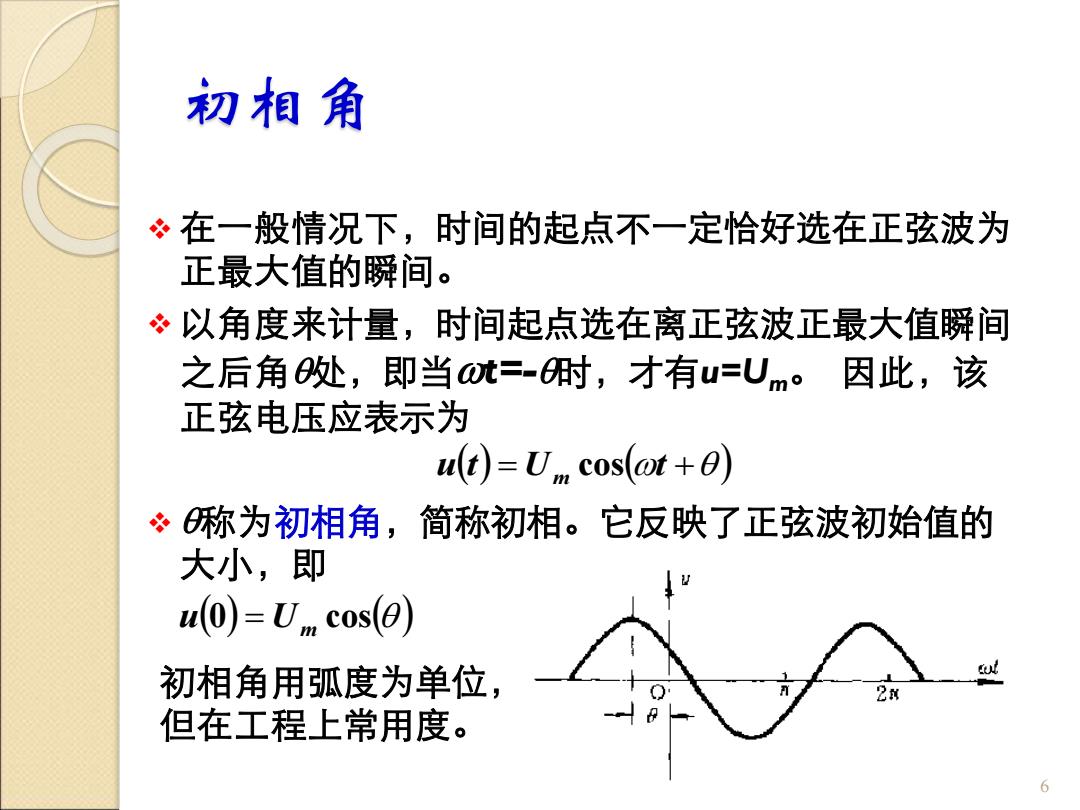
初相角 ❖ 在一般情况下,时间的起点不一定恰好选在正弦波为 正最大值的瞬间。 ❖ 以角度来计量,时间起点选在离正弦波正最大值瞬间 之后角处,即当t=-时,才有u=Um。 因此,该 正弦电压应表示为 ❖ 称为初相角,简称初相。它反映了正弦波初始值的 大小,即 6 u(t) = U (t + ) m cos (0) cos( ) u = Um 初相角用弧度为单位, 但在工程上常用度

相位 冬正弦波的表示式中的(t+O称为相位角,简称相位。 不同的相位对应着不同的瞬时值。因此,相位表示了 正弦波变化的进程。 冬正弦波的一般表示式可写成 u(t)=U cos(@t+e) =U cos(2t+0) -U.co 水 一个正弦波可由三个参数完全确定,这三个参数是: 振幅、频率和初相,这三者称为正弦波的三要素。 >
相位 ❖ 正弦波的表示式中的(t+)称为相位角,简称相位。 不同的相位对应着不同的瞬时值。因此,相位表示了 正弦波变化的进程。 ❖ 正弦波的一般表示式可写成 7 ( ) ( ) ( ) = + = + = + T t U U ft u t U t m m m 2 cos cos 2 cos ❖ 一个正弦波可由三个参数完全确定,这三个参数是: 振幅、频率和初相,这三者称为正弦波的三要素
例2 电压波形如图所示, u(V> ()试求T、及w (2)用cos函数,写出u(t)表示式; 50 ()用sin函数,写出u(e表示式。d 51015202530 (ms) 解(1)从波形图可知,从第一个-1 正最大值到第二个正最大值所需 的时间为 T=22.5-2.5=20s 故得 f- 20×10-3 =50k 0=2d=2π×50=314rd/s 8
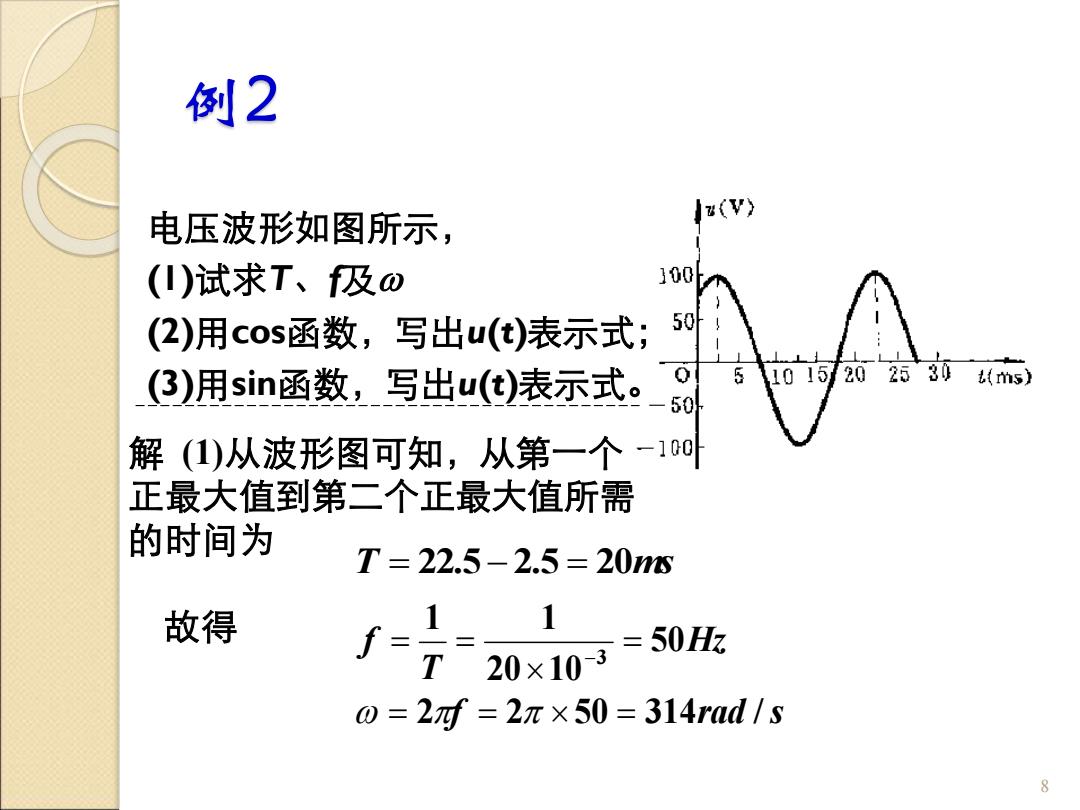
例2 电压波形如图所示, (1)试求T、f及 (2)用cos函数,写出u(t)表示式; (3)用sin函数,写出u(t)表示式。 8 解 (1)从波形图可知,从第一个 正最大值到第二个正最大值所需 的时间为 T = 22.5− 2.5 = 20ms 故得 f rad s Hz T f 2 2 50 314 / 50 20 10 1 1 3 = = = = = = −
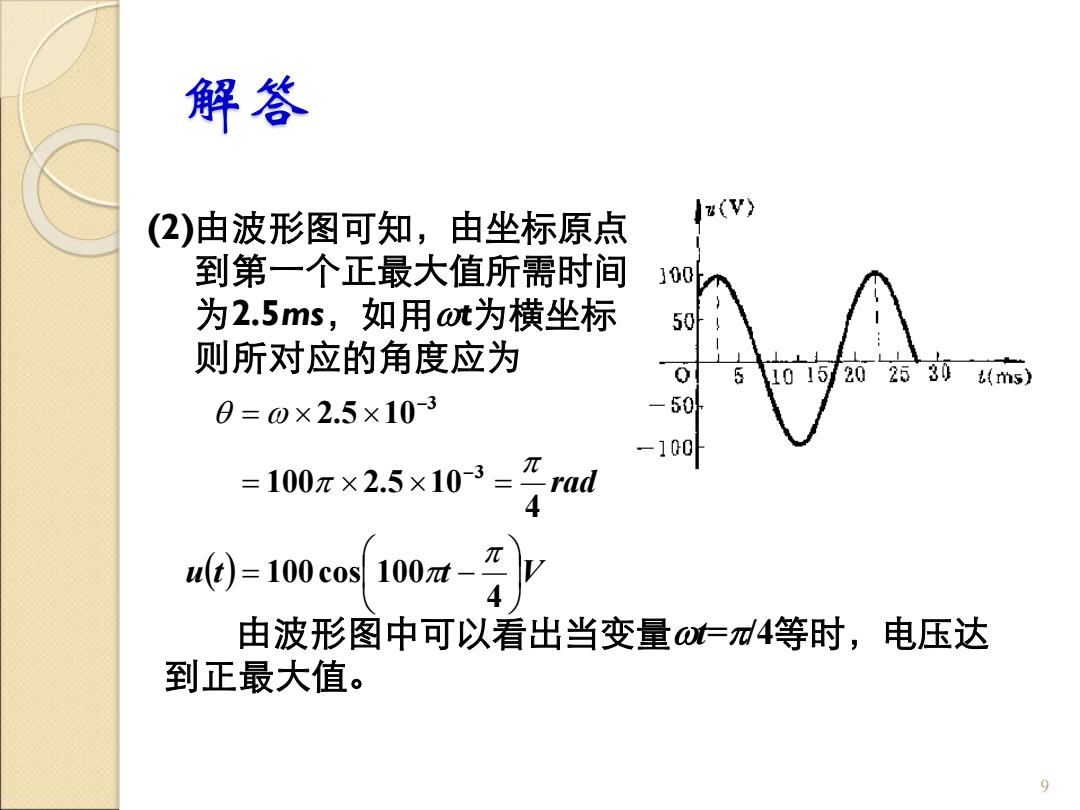
解答 (2)由波形图可知,由坐标原点 u(V) 到第一个正最大值所需时间 300 为2.5ms,如用t为横坐标 50 则所对应的角度应为 0 51015202530 (ms) 0=0×2.5×10-3 50外 -100 =100元×2.5x10-3=元rad 4 40=100cos100t- 4 由波形图中可以看出当变量0仁4等时,电压达 到正最大值
解答 (2)由波形图可知,由坐标原点 到第一个正最大值所需时间 为2.5ms,如用t为横坐标 则所对应的角度应为 9 u(t) t V rad = − = = = − − 4 100cos 100 4 100 2.5 10 2.5 10 3 3 由波形图中可以看出当变量t=/4等时,电压达 到正最大值

解答 (3)如采用si函数来表示正弦波,可用已知的cos函数来 求解,运用三角公式可得 10co:00 =1o0smn0a-子+ 00s10 10
解答 (3)如采用sin函数来表示正弦波,可用已知的cos函数来 求解,运用三角公式可得 10 ( ) t V t V u t t V = + = − + = − 4 100sin 100 4 2 100sin 100 4 100cos 100