
第3单元综合练习 一、我会填。(17分) 1.圆柱的上、下底面是两个面积( )的圆,把圆柱的侧面沿高剪开,如果圆柱的 侧面展开图是一个正方形,那么它的底面周长与它的高( 2.一个圆柱的侧面积是24.8m2,底面积是4m2,它的表面积是( )m2。 3.一个圆柱的底面半径是5cm,高是10cm,它的底面积是( )cm2,侧面积是 ()cm2,体积是()cm3。 4.等底等高的一个圆锥与一个圆柱的体积之和是483,圆锥的体积是( ),圆柱 的体积是()。 5.有一个圆柱,底面直径是8cm,如果高增加3cm,那么它的侧面积增加 ()cm2. 6.用一块长为25.12cm、宽为12.56cm的长方形铁皮,配上半径是( )cm的圆 形铁皮就可以做成一个容积最大的容器,它的容积最大是( )cm3 7.一个圆柱和一个圆锥等底等高,圆锥的体积比圆柱小1.2dm3,那么圆柱的体积是 ()dm3,圆锥的体积是()dm3。 8.将一根长为2m的圆木截成两个小圆木后,表面积增加了48cm2,这根圆木原来 的体积是()cm3。 9.在中国传统建筑中,圆有着广泛的应用,园林中的月亮门便是其中的代表。农家 书屋要修一道围墙(墙的厚度为20cm),原本要用土石40m3,后来多开了一个月亮 门(如图),减少了土石的用量,实际用了( )m3的土石。(得数保留一位小数) 1.6m 10.两个大小相同的量杯中,都盛有450L的水。将等底等高的圆柱与圆锥零件 分别放入两个量杯中,甲水面刻度线如图所示,圆柱的体积是()cm,乙水面刻 度线显示应是( )mL。 K 600mL 3 二、我会判。(正确的画“√”,错误的画“×)(12分) 1.一个圆柱的体积等于和它等底等高的一个圆锥的体积的3倍。 2.长方体、正方体、圆柱和圆锥的体积公式都可以用V=S表示。 ) 3.圆锥的底面积越大,它的体积也就越大。 4.上、下两个底面相等的物体一定是圆柱。 ( 5.底面半径是2cm的圆柱的侧面积和它的体积相等。 6两个圆柱的表面积相等,体积也一定相等。 三、我会选。(12分)
第 3 单元综合练习 一、我会填。(17 分) 1.圆柱的上、下底面是两个面积( )的圆,把圆柱的侧面沿高剪开,如果圆柱的 侧面展开图是一个正方形,那么它的底面周长与它的高( )。 2.一个圆柱的侧面积是 24.8 m2 ,底面积是 4 m2 ,它的表面积是( )m2。 3.一个圆柱的底面半径是 5 cm,高是 10 cm,它的底面积是( )cm2 ,侧面积是 ( )cm2 ,体积是( )cm3。 4.等底等高的一个圆锥与一个圆柱的体积之和是 48 m3 ,圆锥的体积是( ),圆柱 的体积是( )。 5.有一个圆柱,底面直径是 8 cm,如果高增加 3 cm,那么它的侧面积增加 ( )cm2。 6.用一块长为 25.12 cm、宽为 12.56 cm 的长方形铁皮,配上半径是( )cm 的圆 形铁皮就可以做成一个容积最大的容器,它的容积最大是( )cm3。 7.一个圆柱和一个圆锥等底等高,圆锥的体积比圆柱小 1.2 dm3 ,那么圆柱的体积是 ( )dm3 ,圆锥的体积是( )dm3。 8.将一根长为 2 m 的圆木截成两个小圆木后,表面积增加了 48 cm2 ,这根圆木原来 的体积是( )cm3。 9.在中国传统建筑中,圆有着广泛的应用,园林中的月亮门便是其中的代表。农家 书屋要修一道围墙(墙的厚度为 20 cm),原本要用土石 40 m3 ,后来多开了一个月亮 门(如图),减少了土石的用量,实际用了( )m3 的土石。(得数保留一位小数) 10.两个大小相同的量杯中,都盛有 450 mL 的水。将等底等高的圆柱与圆锥零件 分别放入两个量杯中,甲水面刻度线如图所示,圆柱的体积是( )cm3 ,乙水面刻 度线显示应是( )mL。 甲 乙 二、我会判。(正确的画“√”,错误的画“×”)(12 分) 1.一个圆柱的体积等于和它等底等高的一个圆锥的体积的 3 倍。 ( ) 2.长方体、正方体、圆柱和圆锥的体积公式都可以用 V=Sh 表示。 ( ) 3.圆锥的底面积越大,它的体积也就越大。 ( ) 4.上、下两个底面相等的物体一定是圆柱。 ( ) 5.底面半径是 2 cm 的圆柱的侧面积和它的体积相等。 ( ) 6.两个圆柱的表面积相等,体积也一定相等。 ( ) 三、我会选。(12 分)
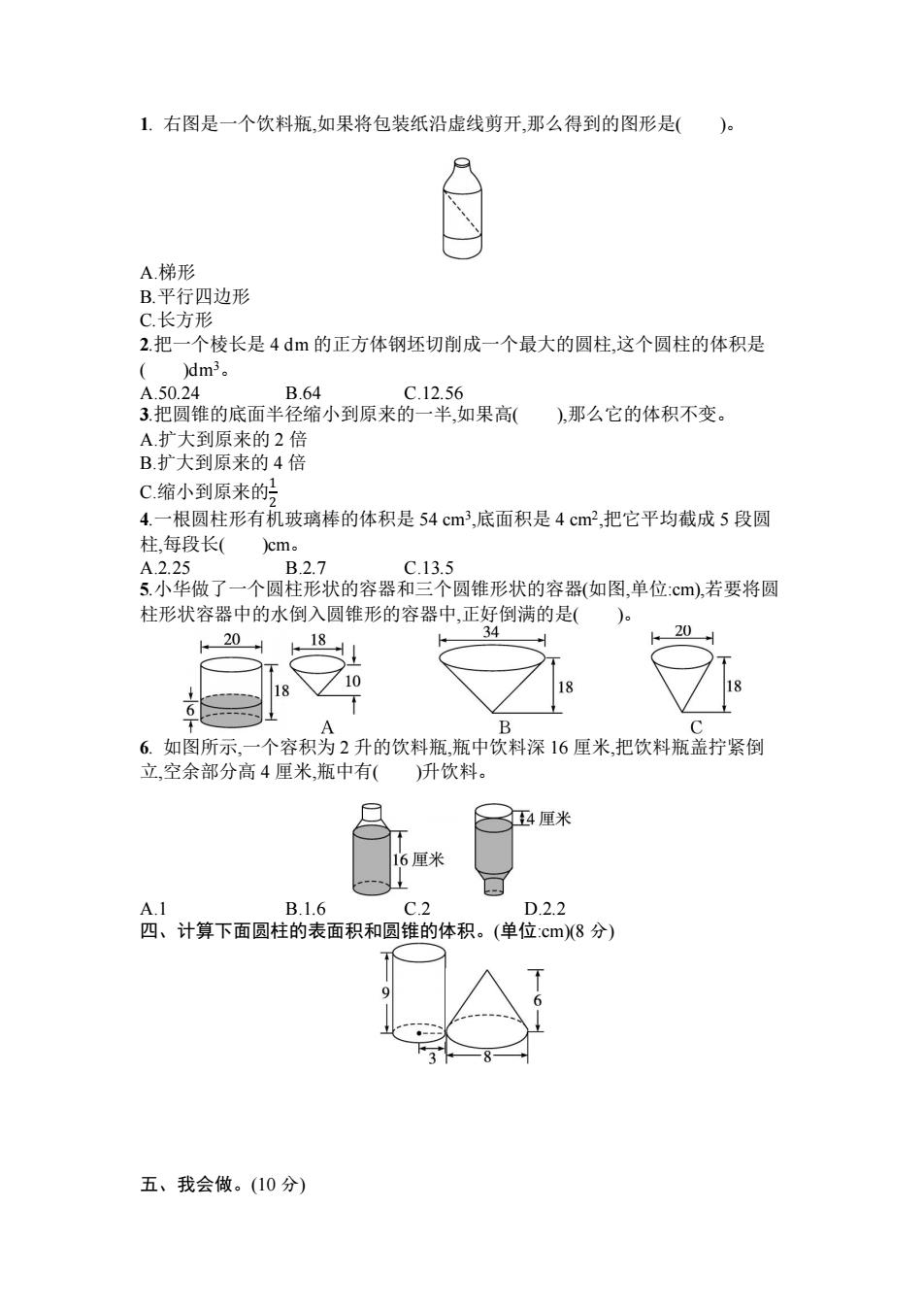
1.右图是一个饮料瓶,如果将包装纸沿虚线剪开,那么得到的图形是()。 A梯形 B.平行四边形 C.长方形 2.把一个棱长是4dm的正方体钢坯切削成一个最大的圆柱,这个圆柱的体积是 ()dm3。 A.50.24 B.64 C.12.56 3.把圆锥的底面半径缩小到原来的一半,如果高( ),那么它的体积不变。 A.扩大到原来的2倍 B.扩大到原来的4倍 C缩小到原来的 4.一根圆柱形有机玻璃棒的体积是54cm3,底面积是4cm2,把它平均截成5段圆 柱,每段长( )cm A.2.25 B.2.7 C.13.5 5.小华做了一个圆柱形状的容器和三个圆锥形状的容器(如图,单位:cm),若要将圆 柱形状容器中的水倒入圆锥形的容器中,正好倒满的是( 20 人 34 20 人 18 0 6 A C 6.如图所示,一个容积为2升的饮料瓶,瓶中饮料深16厘米,把饮料瓶盖拧紧倒 立,空余部分高4厘米,瓶中有( )升饮料。 4厘米 16厘米 A.1 B.1.6 C.2 D.2.2 四、计算下面圆柱的表面积和圆锥的体积。(单位:c)8分) 五、我会做。(10分)
1. 右图是一个饮料瓶,如果将包装纸沿虚线剪开,那么得到的图形是( )。 A.梯形 B.平行四边形 C.长方形 2.把一个棱长是 4 dm 的正方体钢坯切削成一个最大的圆柱,这个圆柱的体积是 ( )dm3。 A.50.24 B.64 C.12.56 3.把圆锥的底面半径缩小到原来的一半,如果高( ),那么它的体积不变。 A.扩大到原来的 2 倍 B.扩大到原来的 4 倍 C.缩小到原来的1 2 4.一根圆柱形有机玻璃棒的体积是 54 cm3 ,底面积是 4 cm2 ,把它平均截成 5 段圆 柱,每段长( )cm。 A.2.25 B.2.7 C.13.5 5.小华做了一个圆柱形状的容器和三个圆锥形状的容器(如图,单位:cm),若要将圆 柱形状容器中的水倒入圆锥形的容器中,正好倒满的是( )。 6. 如图所示,一个容积为 2 升的饮料瓶,瓶中饮料深 16 厘米,把饮料瓶盖拧紧倒 立,空余部分高 4 厘米,瓶中有( )升饮料。 A.1 B.1.6 C.2 D.2.2 四、计算下面圆柱的表面积和圆锥的体积。(单位:cm)(8 分) 五、我会做。(10 分)

1.如图,乐乐给即将过生日的爷爷买了一盒茶叶,想用彩带扎起来,打结处大约共 长12cm,至少需要多长的彩带?(5分) cm 2.把右图直角三角形绕它的一条直角边旋转一周,求得到的立体图形的体积最大 是多少立方厘米?(5分) 2cm 六、数学与生活。(41分) 1.小明今天买了一筒薯片,突然想到了所学的知识,于是他量了量薯片筒的底面 半径和高。(10分) 3 cm 10 cm (1)制作这个薯片筒的侧面标签,至少需要多大面积的纸?(5分) (2)这个薯片筒的体积是多少?(5分)
1. 如图,乐乐给即将过生日的爷爷买了一盒茶叶,想用彩带扎起来,打结处大约共 长 12 cm,至少需要多长的彩带?(5 分) 2. 把右图直角三角形绕它的一条直角边旋转一周,求得到的立体图形的体积最大 是多少立方厘米?(5 分) 六、数学与生活。(41 分) 1. 小明今天买了一筒薯片,突然想到了所学的知识,于是他量了量薯片筒的底面 半径和高。(10 分) (1)制作这个薯片筒的侧面标签,至少需要多大面积的纸?(5 分) (2)这个薯片筒的体积是多少?(5 分)
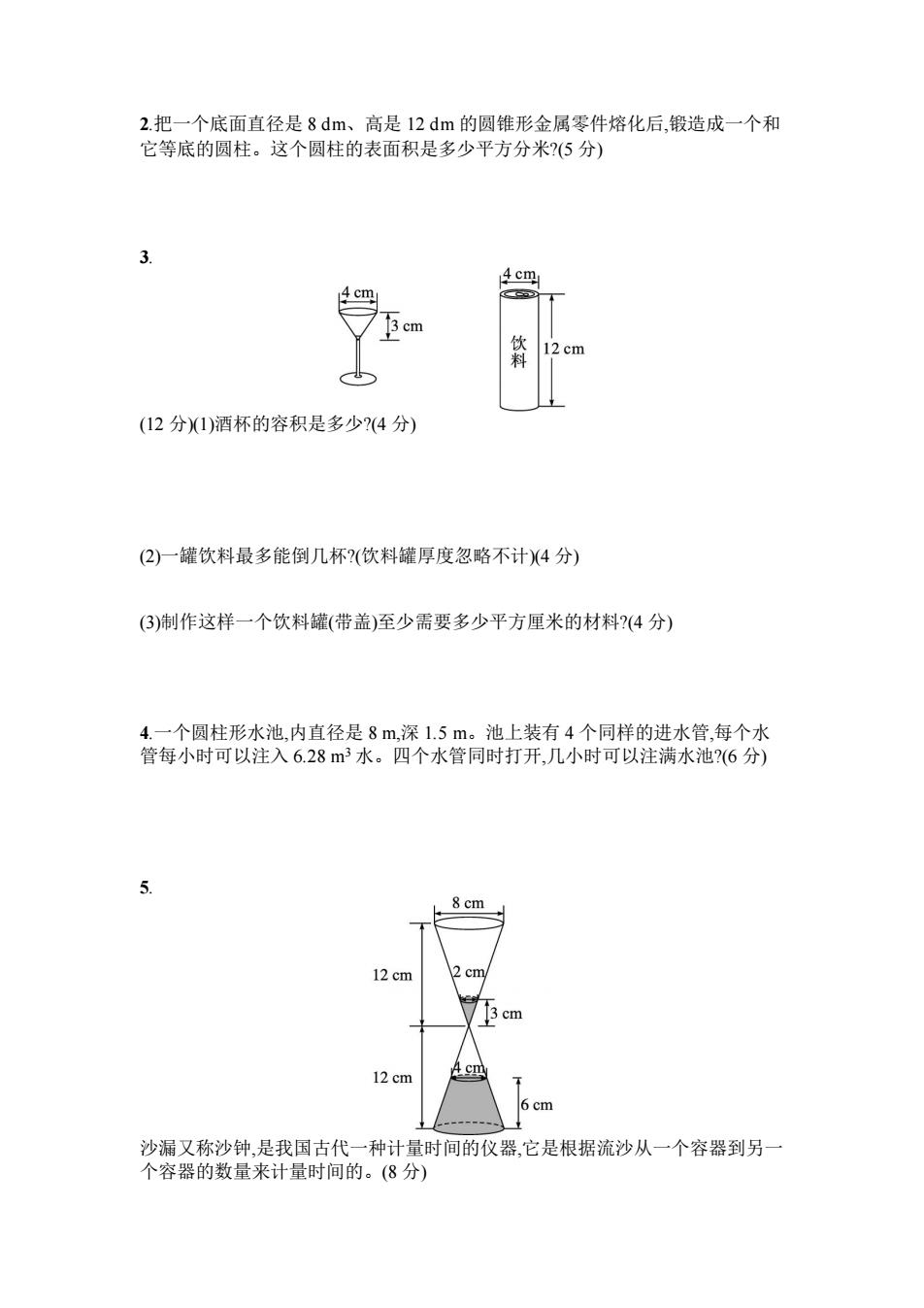
2.把一个底面直径是8dm、高是12dm的圆锥形金属零件熔化后,锻造成一个和 它等底的圆柱。这个圆柱的表面积是多少平方分米?(5分) 3 4 cm 3 cm 饮 12cm (12分1)酒杯的容积是多少?(4分) (2)一罐饮料最多能倒几杯?(饮料罐厚度忽略不计(4分) (3)制作这样一个饮料罐(带盖)至少需要多少平方厘米的材料?(4分) 4.一个圆柱形水池,内直径是8m,深1.5m。池上装有4个同样的进水管,每个水 管每小时可以注入6.283水。四个水管同时打开,几小时可以注满水池?(6分) 8 cm 12 cm 2 cm 3 cm 12 cm A cm 6 cm 沙漏又称沙钟,是我国古代一种计量时间的仪器,它是根据流沙从一个容器到另一 个容器的数量来计量时间的。(8分)
2.把一个底面直径是 8 dm、高是 12 dm 的圆锥形金属零件熔化后,锻造成一个和 它等底的圆柱。这个圆柱的表面积是多少平方分米?(5 分) 3. (12 分)(1)酒杯的容积是多少?(4 分) (2)一罐饮料最多能倒几杯?(饮料罐厚度忽略不计)(4 分) (3)制作这样一个饮料罐(带盖)至少需要多少平方厘米的材料?(4 分) 4.一个圆柱形水池,内直径是 8 m,深 1.5 m。池上装有 4 个同样的进水管,每个水 管每小时可以注入 6.28 m3 水。四个水管同时打开,几小时可以注满水池?(6 分) 5. 沙漏又称沙钟,是我国古代一种计量时间的仪器,它是根据流沙从一个容器到另一 个容器的数量来计量时间的。(8 分)

(1)根据右图,沙漏上部沙子的体积是多少?(4分) (2)如果再过1分钟,沙漏上部的沙子就可以全部漏到下部,那么现在已经计量了 多少分钟?(4分)
(1)根据右图,沙漏上部沙子的体积是多少?(4 分) (2)如果再过 1 分钟,沙漏上部的沙子就可以全部漏到下部,那么现在已经计量了 多少分钟?(4 分)

第3单元综合练习 一、1相等相等 2.32.8 3.78.5314785 4.12m336m3 5.75.36 6.4631.0144 7.1.80.68.4800 9.39.610.150500 二、1.V2.×3.×4.×5.× 6.× 三、1.B2.A3.B4.B5.C6.B 四、3.14×32×2+3.14×3×2×9=226.08(cm2) 3.14×(8÷2Y×6×310,48(cm3) 五、1.(10+5×2)×4+12=92(cm) 23.14×32×2×318.84(cm3) 六、1.(1)3.14×3×2×10=188.4(cm2) (2)3.14×32×10=282.6(cm3) 2.12÷3=4dm) 3.14×8×4+3.14×(8÷2)2×2=200.96(dm2) 313.14目x3×g-12.56cm) 23.14×()×12÷12.56=12(杯) (33.14×f)x2+3.14x4x12=175.84cm) 4.3.14×(8÷22×1.5÷(6.28×4)=3(时) 5.(15×3.14×(2÷2P×3=3.14(cm3) (25×3.14×(8÷22×12=200.96(cm3) 3x3.14×4÷2P×6=25.12(cm)) 200.96-25.12=175.84cm3) 175.84÷3.14=56(分)
第 3 单元综合练习 一、1.相等 相等 2.32.8 3.78.5 314 785 4.12 m3 36 m3 5.75.36 6.4 631.0144 7.1.8 0.6 8.4800 9.39.6 10.150 500 二、1.√ 2.× 3.× 4.× 5.× 6.× 三、1.B 2.A 3.B 4.B 5.C 6.B 四、3.14×3 2×2+3.14×3×2×9=226.08(cm2 ) 3.14×(8÷2)2×6× 1 3 =100.48(cm3 ) 五、1.(10+5×2)×4+12=92(cm) 2.3.14×3 2×2× 1 3 =18.84(cm3 ) 六、1.(1)3.14×3×2×10=188.4(cm2 ) (2)3.14×3 2×10=282.6(cm3 ) 2.12÷3=4(dm) 3.14×8×4+3.14×(8÷2)2×2=200.96(dm2 ) 3.(1)3.14×( 4 2 ) 2 ×3× 1 3 =12.56(cm3 ) (2)3.14×( 4 2 ) 2 ×12÷12.56=12(杯) (3)3.14×( 4 2 ) 2 ×2+3.14×4×12=175.84(cm2 ) 4.3.14×(8÷2)2×1.5÷(6.28×4)=3(时) 5.(1)1 3 ×3.14×(2÷2)2×3=3.14(cm3 ) (2)1 3 ×3.14×(8÷2)2×12=200.96(cm3 ) 1 3 ×3.14×(4÷2)2×6=25.12(cm3 ) 200.96-25.12=175.84(cm3 ) 175.84÷3.14=56(分)