
水质工程学第4章沉淀 第4章沉淀 一.教学目的及要求: 掌握理想沉淀池的沉淀理论、影响半流式沉淀池沉淀效果的因素,熟悉斜板(管)沉淀池、澄清 池及辐流式沉淀池的工作原理:掌握气浮池的气浮原理、熟悉气浮池的构造。 二.教学内容及学时分配(8学时) 4.1杂质颗粒在静水中的沉淀 在给水处理中,常遇到两种沉淀: 1、自由沉淀: 颗粒在沉淀过程中,彼此没有干扰,只受到颗粒本身在水中的重力和水流阻 力的作用,即为自由沉淀。一般认为,固体颗粒与器壁的距离大于50倍颗粒的直 径,同时颗粒的浓度小于5000mgL时,可近似地认为是自由沉淀 2、拥挤沉淀: 颗粒在沉淀过程中,彼此互相干扰,或者受到容器壁的干扰,虽然其粒度和 第一种相同,但沉淀速度却较小,称为拥挤沉淀 一、悬浮颗粒在静水中的自由沉淀 颗粒在静水中的沉淀速度取决于:颗粒所受的重力、浮力和水流阻力,如下 图所示。 颗粒下沉加速度为: (4-1) 式中:Rd,g 为颗粒的重力: 5=石dpg 为颗粒的浮力: 颗粒的水流阻力 F与颗粒的糙度、大小、形状和沉淀速度有关,也与水密度和粘度有关。 将上三式代入(16-1)得: 会名%,小g-Cn号 (4-2 dt 6 式中:CD一阻力系数,与雷诺数有关,CD=∫(Re) 第1负共44贞
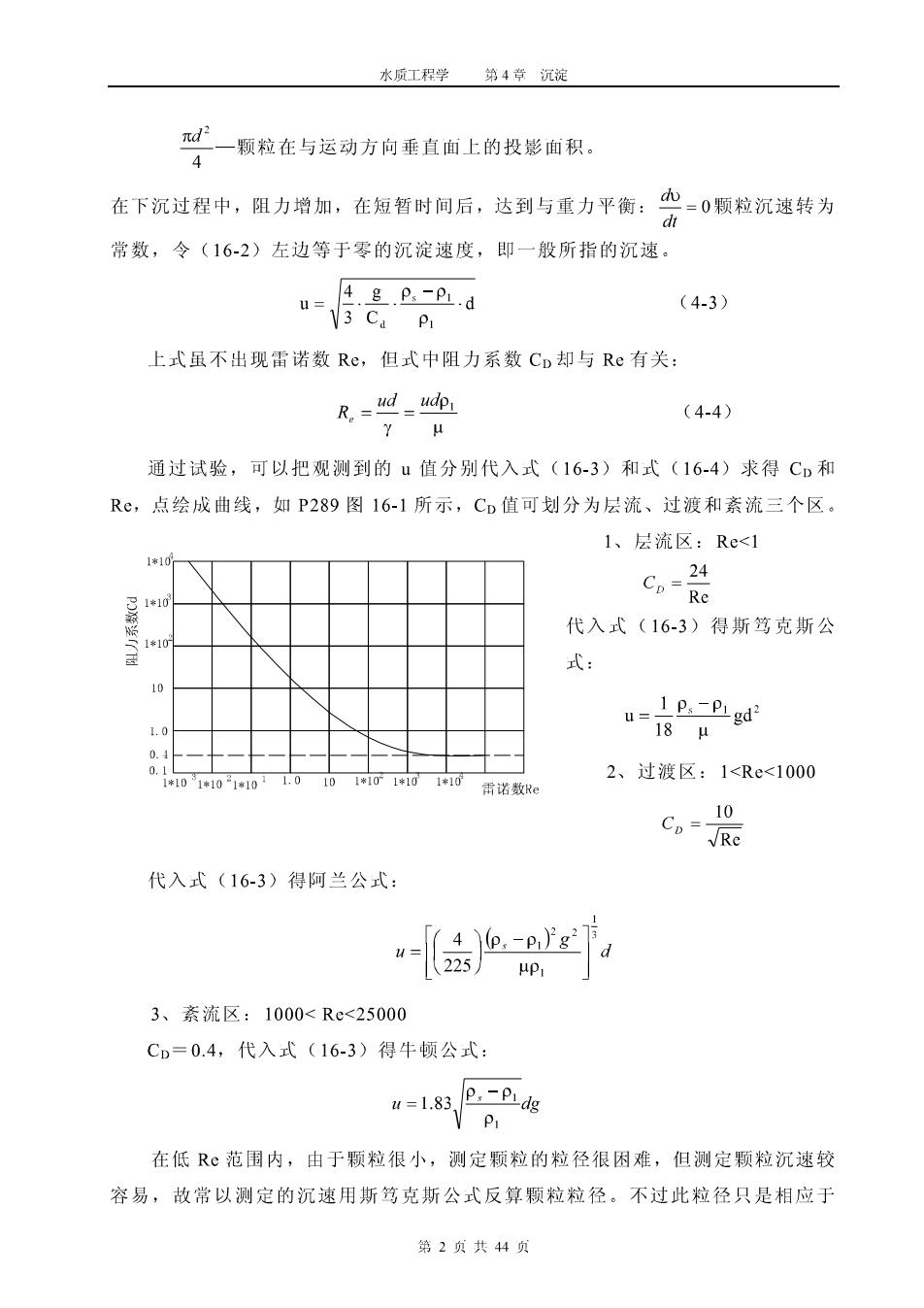
水工程学第4章沉淀 对一颗粒在与运动方向垂直面上的投影面积。 在下沉过程中,阻力增加,在短暂时间后,达到与重力平衡:心=0颗粒沉速转为 常数,令(16-2)左边等于零的沉淀速度,即一般所指的沉速。 4.且.0-.d u=\3 C,P (4-3) 上式虽不出现雷诺数Re,但式中阻力系数CD却与Re有关: R=, (4-4) 通过试验,可以把观测到的u值分别代入式(16-3)和式(16-4)求得CD和 R©,点绘成曲线,如P289图16-1所示,CD值可划分为层流、过渡和紊流三个区 1、层流区:Re<1 1*10 代入式(16-3)得斯笃克斯公 式: 1.0 ”时 0110110110 11110 2、过渡区:1<Re<1000 常诺数R 10 Co=Re 代入式(16-3)得阿兰公式 d 3、紊流区:1000<Rc<25000 Cn=0.4,代入式(16-3)得牛顿公式: 在低R©范围内,由于颗粒很小,测定颗粒的粒径很困难,但测定颗粒沉速较 容易,故常以测定的沉速用斯笃克斯公式反算颗粒粒径。不过此粒径只是相应于 第2共44

水质工程学第4章沉淀 球形颗粒的直径,并非实际粒径。在实用上常用沉速代表某一特定颗粒而不追究 颗粒粒径。 二、悬浮颗粒在静水中的拥挤沉淀 当水中悬浮颗粒浓度很高,颗粒在下沉过程中相互干扰很大时,就产生拥挤沉 淀,此时的沉速称为拥挤沉速 拥挤沉淀有明显的清水和混水的分界血,称为浑液面,浑液面缓慢下沉,直到 泥沙最后完全压实为止。 非凝聚性颗粒当浓度在5000mgL以上时,产生拥挤沉淀,对凝聚性颗粒而言, 由于其比重远小于沙粒的比重,当浓度在3000mg/L左右,也会产生拥挤沉淀。 高浊度水拥挤沉淀过程分析如下: 将高浊度水注入一只透明的沉淀筒中进行静水沉淀,沉淀现象图42(b),整 个沉淀简中可分为四个区:清水区A,等浓度区B,变浓度区C及压实区D,清 水区以下的各区可以总称为悬浮物区或污泥区。 d 时t (a) (b) (c)】 (e) 高浊水的沉降过程 等浓度区:整个等浓度区中的浓度都是均匀的,这一区内的颗粒大小虽然不同, 但由于互相干扰的结果,大的颗粒沉降变慢了,而小的颗粒沉降却变快了,因而 形成等速下沉的现象,整个区似乎都是由大小完全相符的颗粒组成的。当最大粒 度与最小粒度之比约为6:1以下时,就会出现这种等速下沉的现象 消水区:颗粒等速下沉的结果,在沉淀筒内出现了一个清水区,清水区和等浓 度区之间形成一个清晰的交界血,称为浑液面。它的下沉速度代表了颗粒的平均 沉降速度。颗粒间的絮凝过程越好,交界面就越清晰,清水区内的悬浮物就越少。 压实区:紧靠沉淀筒底部的悬浮物很快就被管底截住,这层被截住的悬浮物又 第3负共44贞

水质工程学4章沉淀 反过来干扰上面的悬浮物沉淀过程,同时在底部出现一个压实区。压实区内的悬 浮物有两个特点:一个是从压实区的上表面起到管底上,颗粒沉降的速度是逐渐 减小的,在管底的颗粒沉降速度为零:二是由于简底的存在,压实区内悬浮物缓 慢下沉的过程,也就是这一区内悬浮物缓慢压实的过程 过渡区:从压实区与等浓度区的特点比较,就可以看出它们之间必然存在一个 过渡区,即一个从等浓度区的浓度逐渐变为压实区顶部浓度的区域。 在沉淀过程中,清水区高度逐渐增加,压实区高度也逐渐增加,而等浓度区的 高度逐渐消失,最后不复存在。变浓度区的高度开始是基本不变的,但当等浓度 区消失后,也就逐渐消失。变浓度区消失后,压实区内仍然继续压实,直到这 区的悬浮物达到最大密度为止。当沉降达到变浓度区刚消失的位置时,称为临界 沉降点。 沉淀试验的目的是求出等浓度区的浓度以及沉淀过程线,即交界面沉降过程 线,如图4-2(c)所示。 a一b段:为上凸的曲线,这是由于颗粒凝聚度变大,使下降速度逐渐变大。 b一c段:为直线,表明交界血等速下降,一直到c点(当浑水自然沉淀时 abc段基本上是一直线)。 c一d段:为下凹的曲线,表明交界面下降速度逐渐变小。此时B区和C区已 消失,c点称为沉降临界点,交界面下的浓度均大于C。(原水浓度),C一d段表示 B、C、D三区重合后,沉淀物的压实过程。随着时间的增长,压实变慢,最后压 实到高度H为止。 B区交并发 如用同一水样,用不同高度的水深做实 验,见下图,发现在不同沉淀高度H,及H 时,两条沉降过程曲线之间存在着相似关 系,说明当原水浓度相同时,A、B区交界 的浑液面的下沉速度是不变的,但由于沉淀 水深高时,最后沉淀物的压实要比沉淀水深 沉时时 底时的压得密实些。由于这种沉淀过程与沉淀高度无关,这样就可以用较短的沉 淀管做实验,来推测实际沉淀浓缩的沉淀效果。 关于用形象化的图形来解释拥挤沉淀的过程(略) 沉淀开始时的浓度C和高度的乘积代表了水中泥沙的总含量,同样在沉淀 第4共4页

水质工程学4章沉淀 时间t时刻,水中泥沙的总含量应该等于平均浓度C和高度H的乘积。则得: HC。=HC 式中:C一高度H内的平均浓度。 显然,C>交养面浓度C,在高度H内的浓度是由交界面的浓度C向下逐渐加 大的,只有当H达到H,即Ct也达到C,C与Ct才相等。 由沉降过程曲线可以求出交荞面上任一点的悬浮物浓度和这一点的沉降速度 (即这一点悬浮物的沉降速度)。如果在交界面上的Ct点(交券面的浓度即为C) 作一条切线与纵坐标相交,得高度H,按照肯奇沉淀理论可得 q=4,C (4-11) HI 上式说明:高度Ht、均匀浓度Ct的沉淀管中所含的悬浮物量和原来的沉淀高 度为H,均匀浓度为C。的沉淀管中所含的悬浮物量相等。 这条切线的斜率即代表浓度为C:的交界面下沉速度, 心,=4-H 式(4-11)的推导比较复杂,可以结合上图沉降曲线的两端作一个简单的证明。 在b-c段,因切线是b-c直线,Ht=Ho,所以Ct=Co。由于b-c线的斜率不变, 也说明了浑液面等速下沉。压缩到高度H后,斜率为零,即片为零。说明不再压 实,此时,C即等于最后压实浓度C。 4.2平流沉淀池 投药 投药 平流沉淀池应用很广,特别 是在城市水厂常被采用。 原水一 混台絮凝一沉淀 过滤 平流式沉淀池基本组成 冷却水 进水区:原水均匀分配。 沉淀区:分离沉淀。 出水区:缓慢出水。 积泥区:污泥浓缩,排出池外 沉淀池在运行时,水流受到池身构造和外养影响(如进口处水流惯性、出口 第3负共44贞

水质工程学4章沉淀 处束流、池面风吹、水质的浓差和温度等),致使颗粒沉淀规律复杂化。为此,先 讨论理想沉淀池,然后讨论实际情况:此外,凝聚性颗粒在下沉时,颗粒间由于 碰撞接触而结成大颗粒,沉速增加,也使沉淀规律复杂化。以下先从非凝聚性颗 粒的沉降规律出发再讨论凝聚性颗粒 一、非凝聚性颗粒地沉淀过程分析 理想沉淀池应符合三个假定: 1、颗粒处于自由沉淀状态:即在沉 淀过程中,颗粒之间互不干扰,颗粒的大 小、形状和密度不变。因此,颗粒的沉速 始终不变。 2、水流沿着水平方向流动。在过水 断面上,各点流速相等。并在流动过程中 流速始终不变。 3、颗粒沉到池底即认为已被去除,不再返回水流中。 按照上述假定,理想沉淀池底工作情况见上图。原水进入沉淀池,被均匀分 配在进水区的A一B截面上,其水平流速为: 式中:V一一水平流速,ms。 Q一一流量,m3/s。 ho一一水流截面A一B的高度,m。 B一一水流截面的宽度,B。 如图所示,直线I代表从池顶A点开始下沉而能够在池底最远处B点前沉到 池底的颗粒的运动轨迹:直线Ⅱ代表从池顶A开始下沉而不能沉到池底的颗粒的 运动轨迹:直线Ⅲ代表一种颗粒从池顶A开始下沉而刚好沉到池底是远处B点的 运动轨迹。 设沉淀池的水平流速为V,则得按直线Ⅲ运动的颗粒的相应沉速为。 因此,凡是沉速u>的一切颗粒都可以沿着类似直线I的方式沉到池底,凡 是u<的颗粒,如从池顶A点开始下沉,肯定不能沿到池底而沿者类似直线Ⅱ的 方式被带出池外。由此可见,直线Ⅲ所代表的颗粒的沉速具有特殊的意义,称 第6共4负

水质工程学4章沉淀 为截留沉速。实际上它反映了沉淀池所能全部去除的颗粒中的最小颗粒的沉速 即凡是沉速≥的颗粒能够全部下沉而被去除。 (二)表面负荷率 对于直线Ⅲ所代表的一类颗粒而言,流速v和与沉淀时间t有关。 I=LN 式中:L一一沉淀区的长度,m:ho一一沉淀区的水深,m: t一一水在沉淀区中的停留时间,s: 令上式两式相等,得: 光品品 上式中LB是沉淀池水面的表面积A,因此,上式的右边就是单位沉淀池表面 积的产水量,可用下式表示: uo=Q/A (4-17) 式中:Q/A称为“表面负荷率”或“溢流率”,上式表明,表面负荷率在数值 上等于截留沉速:但含义不同,后者代表自池顶A开始下沉所能全部去除的颗粒 的最小颗粒的沉速。 (二)沉淀效率 1、某一特定颗粒即具有沉速山的颗粒的去除百分比E。 应该指出,这个特定颗粒的沉速必是小于,因为≥的颗粒将全部下沉。 去除率E的关系推导如下: 因为u<的颗粒如从池顶A点下沉,将沿直线Ⅱ前进而不能沉到池底,引一 条平行与直线Ⅱ而交于B的直线mB。图4-4可见,只有位于池底以上:高度内, 即处于m点以下的这种颗粒(特定颗粒u,<)才能全部沉到池底。设原水中这种 颗粒的浓度为C,沿进入的这种颗粒的总量为 QC=hoBvC 沿m点以下的高度hi截面进入的这种颗粒的数量为hBvC,则沉速为u,的颗 粒的去除率应为: E=(hiBvC)/(hoBvC)=hi/ho (4-18) 又△ABB'∽△Abb'得:hMo=LN即h=LW 同理△mBB'∽△mcc'得:h/u:=L/w 即h=Lwy 第7负共44贞

水顾工程学4章沉淀 将上两式代入式(16-18)得去除率公式为: E=-丛-4 (4-22) uo Q/A 由上式可知:悬浮颗粒在理想沉淀池中的去除率只与沉淀池的表面负荷率有 关,而与其它因素如水深、水平流速和沉淀时间均无关。这一理论早在1904年, 由哈真(Haz心)提出。在实际沉淀池中,除表血负荷率外,其它许多因素对去除 率还是有影响的,这将在后面讨论。 由式(4-22)得出两点结论: 1)当E一定时,u,越大,则Q/A越高,亦即产水量越大:或者当产水量和表 面积不变时,山:越大,则E越高。颗粒沉速的大小与凝聚效果有关。所以生产 上均重视反应工艺。 2)当山,一定时,增加沉淀池表面积可以提高去除率(E增大),当沉淀池容 积一定时,池身浅些则表面积大些,去除率可以提高,此即所谓浅池理论,斜板 斜管沉淀池的发展即基于此理论。 2、沉淀池总的沉淀效率 以上讨论的是某一种特定的“具有沉速山的颗粒”(u<uo)的去除率,实际 上,原水中具有小于的颗粒尺寸众多,这些不同的颗粒的总去除率是各别颗粒 去除率的总和 设P,为所有小于山,的颗粒重量占原水中全部颗粒重量的百分率,显然p,为 具有沉速u,的一种颗粒重量占原水中全部颗粒重量的百分率,根据式(4-22),能 够在沉淀池中下沉的这种具有沉速山,的颗粒重量占原水中全部颗粒重量的百分率 应为兰p,因此,所有能够在沉淀池中下沉的,沉速小于山的颗粒重量占原水中 全部颗粒重量的百分率应为: B=8, 另外,沉速≥的颗粒已经全部下沉,其去除率应为1一P。因此,理想沉淀 池总的去除率,即沉淀池的沉淀效率p为: P=0-R)+, (4-24) 第8负共4负

水质工程学第4章沉淀 式中:P。一一所有沉速小于理想沉淀池截留沉速的颗粒重量占原水中全部颗粒 重量的百分率。 uo一一理想沉淀池的截留速度。 u一一小于截留沉速的颗粒沉速 p,一一所有沉速小于山的颗粒重量占原水中全部颗粒重量的百分率: dp,一一具有沉速为山的颗粒重量占原水中全部颗粒重量的百分率。 3、非凝聚颗粒在静水中的沉淀试验 这种试验一般用一圆筒进行。如图 45所示,在圆筒水面下处开一取样口。 取样开始(t=0)时,浓度沿水深均匀分 布为Co,然后分别在t、t2…t等时刻 取样,分别测得浓度为C、C2…Ca。 假定在取样过程中,水面位置基本不变, 沉=h/t 那么,在时间恰好是、t2…t等时, 沉速为ht=u,h/t2=u2,…h/tn=u,等颗粒就恰好通过取样口向下沉,相应地这 些颗粒在高度中不复存在了,也即所取出的水样中已没有这些相应的颗粒。如 果以P1、P2,…Pn等分别代表C/C,C2Co,…CCo,那么它们就代表在取 样口处的水样中所残存的悬浮颗粒的浓度百分数,也即小于该沉速的颗粒浓度分 数,(1一P1,1一p2…1一p等分别代表取样口水样中已经去除的悬浮颗粒分数)。 点绘出P一u曲线。 从图上可见,具有沉速为1,2,(u1>u≥u2)的两种颗粒之间的颗粒浓度百 分数为p1一p2。如果两种颗粒无限接近为具有u的特定颗粒,那么其含量为dp 则沉速为u,<的颗粒去除率为u,/o·dp,则所有沉速小于o的颗粒去除率百分 率为邮,则沉淀池的沉淀效率为: (- 4、式(4-24)的其它理解 设想沉淀管水深与沉淀池水深一样,并从沉淀开始(=0)把沉淀管放在沉淀 池的进口断面,水面相齐,并以沉淀池的水平流速ⅴ随着前进,见下图。这样 第9贞共44贞

水质工程学第4章沉淀 沉淀管中各种颗粒下沉的过程必然也和沉淀池水中的各种颗粒下沉的过程相同 沉速为,2,…u的颗粒分别沿着它们与水平流速的合成速度方向下降。 从进口水面开始,各种颗粒下沉的轨迹线可以看作为一族代表相应的颗粒(即 一种颗粒一条轨迹线),以及大于它的颗粒被去除的累积百分数线。 在图中,纵坐标为水深山,横坐标有三种表示方法:1)沉淀池水平方向的距 离:2)各种颗粒的沉淀时间: 3)各种颗粒的沉速u=ht。 图中Au线为具有沉速u 颗粒下沉的轨迹线,颗粒在 悬浮物占100p1%,被100%的 去除掉,故A山1线代表悬浮物 被去除100p1'%=100p1%的 线,可表示为p1'线。Au2为2 凝聚性颗粒去除百分数 颗粒下沉的轨迹,2颗粒占 100p2%,也是100%地被去掉,实际上Au2线可视作u1及u2颗粒被100%去除的 紫计百分数线,可表示为100p2'%=100(p1+p2)%。设为沉淀池的截留沉速, 占悬浮物总量中的100p0%,那末,沉淀池可以100%去除的累积百分数,可表示 为100p0%=100(p1+p2+…+po)%。至于比uo为小的颗粒只能部分的被去除。如 u-k的颗粒占Pn-k%,那末山a-k颗粒被去除的百分数占悬浮物总量的(仙n ko)I00pk%,其累积去除百分数为(即Auw线所代表的悬浮物去除百分数): 100pa-k'%=100[p1+p2+…+p0+(un-k/uo)pm-k]% 这些去除百分数线都是直线,可以通过试验得出,如上图所示。去除百分数 线的物理涵义也可以这样描述:一条去除百分数线表示了沉淀池100%去掉的颗粒 中的最小颗粒的运动轨迹,也就是这些颗粒能够下沉的最远途径。 由图16-9可见,当沉淀池沉淀时间为1,也即截留速度为时,去除悬浮物 总量的百分数可表示为: p=po'+ua-k/uo(Pa-k'-po)+....+ua-2/uo(pa-2'-pa=3') tua-1/uo(pa-1'-Pa-2')tu/(1-pa-1') (4-25) 上式为式(4-24)的另一种表示形式,根据式(4-25),将沉淀数据加以整理 即可得出总去除百分数 第10贞共4贞