
例6-1苯(A)与甲苯(B)的饱和蒸气压和温度的关系数据如本题附表1所式。 试利用拉乌尔定律和相对挥发度,分别计算苯一甲苯混合液在总压P为 101.33kPa下的气液平衡数据,并作出温度一组成图。该溶液可视为理想溶液 例6-1 附表1 温度,℃80.1859095100105110.6 p4,kPa101.33116.9135.5155.7179.2204.2240.0 p8,kPa40.046.054.063.374.386.0101.33 解:(1)利用拉乌尔定律,计算气液平衡数据在某一温度下由本题附表 1可查得该温度下纯组分苯与甲苯的饱和蒸气压PA与PB,由于总压P为定值, P-PB. 即P=101.33kPa,则用式 区ApP求液相组成再应用式4宁不求平 衡的气相组成y,即可得到一组标绘平衡温度一组成(t-xy)图的数据。 以t=95℃为例,计算过程如下: 不A= 2-p.=10133-633=0.412 p9-p8155.7-63.3 和4-=各4-8弱042=063 其它温度的计算结果列于本题附表2中。 例6-1附表2 t,℃80.1 859095100105110.6 x1.000 0.7800.5810.4120.2580.1300 y1.000 0.9000.7770.6330.4560.2620 根据以上数据,即可标绘得到如图所示的t一xy图
例 6-1 苯(A)与甲苯(B)的饱和蒸气压和温度的关系数据如本题附表 1 所式。 试利用拉乌尔定律和相对挥发度,分别计算苯—甲苯混合液在总压 P 为 101.33kPa 下的气液平衡数据,并作出温度—组成图。该溶液可视为理想溶液。 例 6-1 附表 1 温度,℃ 80.1 85 90 95 100 105 110.6 ,kPa 101.33 116.9 135.5 155.7 179.2 204.2 240.0 ,kPa 40.0 46.0 54.0 63.3 74.3 86.0 101.33 解:(1)利用拉乌尔定律,计算气液平衡数据 在某一温度下由本题附表 1 可查得该温度下纯组分苯与甲苯的饱和蒸气压 与 ,由于总压 P 为定值, 即 ,则用式 求液相组成 x,再应用式 求平 衡的气相组成 y,即可得到一组标绘平衡温度—组成(t-x-y)图的数据。 以 为例,计算过程如下: 和 其它温度的计算结果列于本题附表 2 中。 例 6-1 附表 2 t,℃ 80.1 85 90 95 100 105 110.6 x 1.000 0.780 0.581 0.412 0.258 0.130 0 y 1.000 0.900 0.777 0.633 0.456 0.262 0 根据以上数据,即可标绘得到如图所示的 t-x-y 图
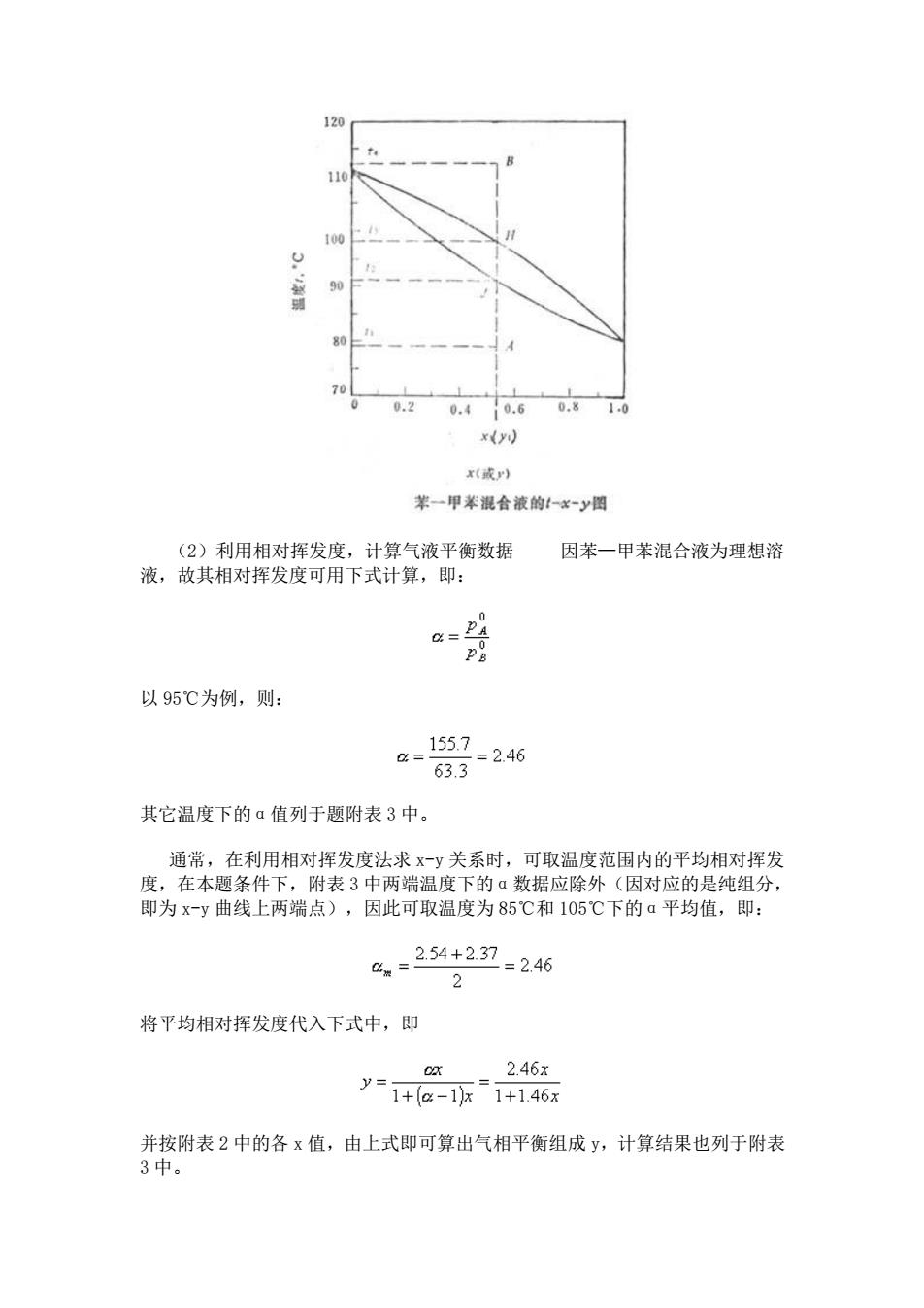
90 0.20.40.60.810 羊一甲苯混合液的一x-y国 (2)利用相对挥发度,计算气液平衡数据 因苯一甲苯混合液为理想溶 液,故其相对挥发度可用下式计算,即: a=pa p月 以95℃为例,则: 器-26 其它温度下的α值列于题附表3中。 通常,在利用相对挥发度法求xy关系时,可取温度范围内的平均相对挥发 度,在本题条件下,附表3中两端温度下的▣数据应除外(因对应的是纯组分, 即为x-y曲线上两端点),因此可取温度为85℃和105℃下的a平均值,即: 8,-254+237=246 2 将平均相对挥发度代入下式中,即 246 y=1+a-11+146 并按附表2中的各x值,由上式即可算出气相平衡组成y,计算结果也列于附表 3中
(2)利用相对挥发度,计算气液平衡数据 因苯—甲苯混合液为理想溶 液,故其相对挥发度可用下式计算,即: 以 95℃为例,则: 其它温度下的α值列于题附表 3 中。 通常,在利用相对挥发度法求 x-y 关系时,可取温度范围内的平均相对挥发 度,在本题条件下,附表 3 中两端温度下的α数据应除外(因对应的是纯组分, 即为 x-y 曲线上两端点),因此可取温度为 85℃和 105℃下的α平均值,即: 将平均相对挥发度代入下式中,即 并按附表 2 中的各 x 值,由上式即可算出气相平衡组成 y,计算结果也列于附表 3 中

比较本题附表2和附表3,可以看出两种方法求得的x-y数据基本一致。对 两组分溶液,利用平均相对挥发度表示气液平衡关系比较简便。 例6-1附表3 t,80.1 90 95 100 105 110.6 a2.54 2.51 2.46 2.41 2.37 1.000 0.780 0.581 0.412 0.258 130 0 1.000 y269 0.897 0.773 0.633 0.461 0 例6-2对某两组分理想溶液进行常压闪蒸,已知?为0.5(原料液中易挥发组 分的摩尔分率),若要求气化率为60%,试求闪蒸后平衡的气液相组成及温度。 常压下该两组分理想溶液的xy及t。一x关系如本例附图所示。 解:由题意知1-9=06 g0.4 所以9=04,9-706-067 在本例附图(x-y图)中通过 点e(0.5,0.5)作斜率为-0.66 的直线ef,由该直线与x-y平衡 曲线交点f的坐标,即可求得平 衡的气液相组成,即: x≈0.387 y≈0.575 再由附图中t。~x曲线,从 x=0.387可求得平衡温度,即 4=113℃ 例6-3对例6-2中的液体混合物进行简单蒸馏,若气化率仍为60%,试求釜残液 组成和溜出液平均组成。已知常压下该混合液的平均相对挥发度为2.16。 解:设原料液量为100kmo1,则: D=100×0.6=60 kmol
比较本题附表 2 和附表 3,可以看出两种方法求得的 x-y 数据基本一致。对 两组分溶液,利用平均相对挥发度表示气液平衡关系比较简便。 例 6-1 附表 3 t, ℃ 80.1 85 90 95 100 105 110.6 α 2.54 2.51 2.46 2.41 2.37 x 1.000 0.780 0.581 0.412 0.258 0 .130 0 y 1.000 0.897 0.773 0.633 0.461 0 .269 0 例 6-2 对某两组分理想溶液进行常压闪蒸,已知 为 0.5(原料液中易挥发组 分的摩尔分率),若要求气化率为 60%,试求闪蒸后平衡的气液相组成及温度。 常压下该两组分理想溶液的 x-y 及 te-x 关系如本例附图所示。 解:由题意知 所以 , 在本例附图(x-y 图)中通过 点 e(0.5,0.5)作斜率为-0.667 的直线 ef,由该直线与 x-y 平衡 曲线交点 f 的坐标,即可求得平 衡的气液相组成,即: 再由附图中 te~x 曲线,从 可求得平衡温度,即 例 6-3 对例 6-2 中的液体混合物进行简单蒸馏,若气化率仍为 60%,试求釜残液 组成和馏出液平均组成。已知常压下该混合液的平均相对挥发度为 2.16。 解:设原料液量为 100kmol,则:

W=F-D=100-60=40mol 因该混合液平均相对挥发度为=2.16,则可用下式求釜残液组成x2,即: 试差解得:x3≈0.328 馏出液平均组成可由下式求得: D=F名1-W3 即:605=100×0.5-40×0.328 所以卫=0.614 计算结果表明,若气化率相同,简单蒸馏较平衡蒸馏可获得更好的分离效果 即馏出液组成更高。但是平衡蒸馏的优点是连续操作。 例6-4每小时将15000kg含苯40%(质量%,下同)和甲苯60%的溶液,在连续 精馏塔中进行分离,要求釜残液中含苯不高于2%,塔项馏出液中苯的回收率为 97.1%。试求馏出液和釜残液的流量及组成,以摩尔流量和摩尔分率表示。 解:苯的分子量为78:甲苯的分子量为92。 40/78 进料组成: 4078+6092=0,4 278 釜残液组成: m-278+9g92=0023 原料液的平均分子量:Mx=0,44×78+0.56×92=85.8 原料液流量:F=15000/85.8=175.0kmo% 依题意知:DxD/Fx,=0.971 所以:Dx=0,971x175×0.44(a)
因该混合液平均相对挥发度为 ,则可用下式求釜残液组成 x2,即: 或 试差解得: 馏出液平均组成可由下式求得: 即: 所以 计算结果表明,若气化率相同,简单蒸馏较平衡蒸馏可获得更好的分离效果, 即馏出液组成更高。但是平衡蒸馏的优点是连续操作。 例 6-4 每小时将 15000kg 含苯 40%(质量%,下同)和甲苯 60%的溶液,在连续 精馏塔中进行分离,要求釜残液中含苯不高于 2%,塔顶馏出液中苯的回收率为 97.1%。试求馏出液和釜残液的流量及组成,以摩尔流量和摩尔分率表示。 解:苯的分子量为 78;甲苯的分子量为 92。 进料组成: 釜残液组成: 原料液的平均分子量: 原料液流量: 依题意知: 所以: (a)

全塔物料衡算D+W=F=175(b) Dxp +Wxw =Fxt 或Dr,+0.0235W=175x0.44(c) 联立式a、b、c,解得: D=80.0kmol/h W=95.0 kmoi/h xp=0.935 例6-5分离例6-4中的溶液时,若进料为饱和液体,选用的回流比R=20,试 求提馏段操作线方程式,并说明操作线的斜率和截距的数值。 解:由例6-4知: xw =0.0235,D=80.0 kmol/h W=95.0 kmolfh F=175kmol/h 而L=RD=2.0×80=160kmol/h 因泡点进料,故: lv-1: 将以上数值代入下式,即可求得提馏段操作线方程式: LtaF W 人1-0751m+72-95*0235 95 或》1=1.4x%-0.0093 该操作线的斜率为1.4,在y轴上的截距为-0.0093。由计算结果可看出,本 题提馏段操作线的截距值是很小的,而一般情况下也是如此的。 例6-6用一常压操作的连续精馏塔,分离含苯为0.44(摩尔分率,以下同)的 苯一甲苯混合液,要求塔顶产品中含苯不低于0.975,塔底产品中含苯不高于 0.0235。操作回流比为3.5。试用图解法求以下两种情况时的理论板层数及加料 板位置。 (1)原料液为20℃的冷液体
全塔物料衡算 (b) 或 (c) 联立式 a、b、c,解得: 例 6-5 分离例 6-4 中的溶液时,若进料为饱和液体,选用的回流比 ,试 求提馏段操作线方程式,并说明操作线的斜率和截距的数值。 解:由例 6-4 知: , 而 因泡点进料,故: 将以上数值代入下式,即可求得提馏段操作线方程式: 或 该操作线的斜率为 1.4,在 y 轴上的截距为-0.0093。由计算结果可看出,本 题提馏段操作线的截距值是很小的,而一般情况下也是如此的。 例 6-6 用一常压操作的连续精馏塔,分离含苯为 0.44(摩尔分率,以下同)的 苯—甲苯混合液,要求塔顶产品中含苯不低于 0.975,塔底产品中含苯不高于 0.0235。操作回流比为 3.5。试用图解法求以下两种情况时的理论板层数及加料 板位置。 (1)原料液为 20℃的冷液体
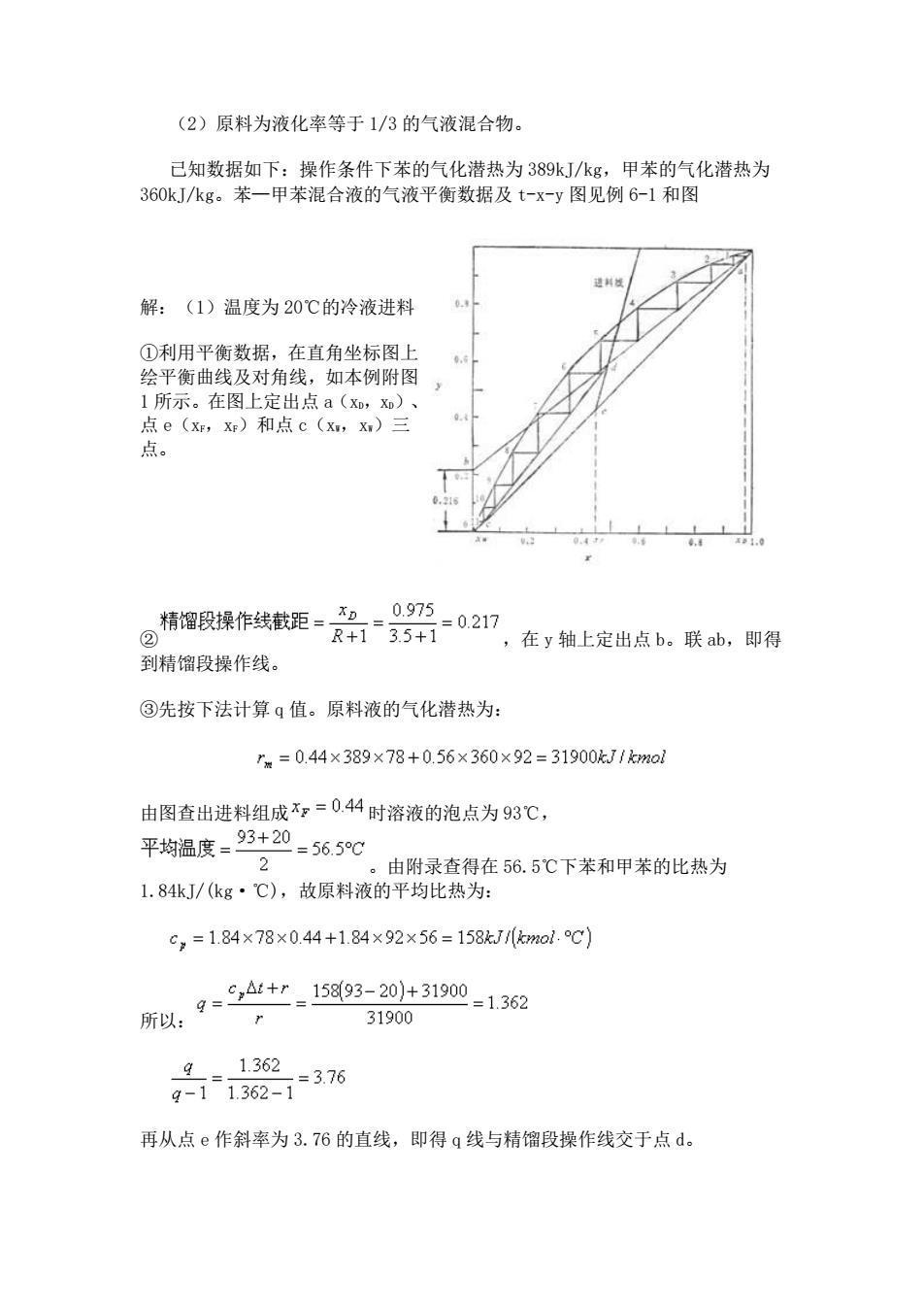
(2)原料为液化率等于1/3的气液混合物。 己知数据如下:操作条件下苯的气化潜热为389kJ/kg,甲苯的气化潜热为 360kJ/kg。苯一甲苯混合液的气液平衡数据及tx-y图见例6-1和图 解:(1)温度为20℃的冷液进料 ①利用平衡数据,在直角坐标图上 绘平衡曲线及对角线,如本例附图 1所示。在图上定出点a(xD,)、 点e(X,x)和点c(x,x)三 包指塑联提作线载距=名-0-02 ”,在y轴上定出点b。联ab,即得 到精馏段操作线。 ③先按下法计算q值。原料液的气化潜热为: ”m=0.44×389×78+0.56×360×92=31900kJ1km01 由图查出进料组成?=044时溶液的泡点为93℃, 平均温度=93+20-5659℃ 2 由附录查得在56.5℃下苯和甲苯的比热为 1.84kJ/(kg·℃),故原料液的平均比热为: c,=1.84×78×0.44+1.84×92×56=158kJwo1.℃) 所.95中31现 31900 g1.362 9-71362-376 再从点e作斜率为3.76的直线,即得q线与精馏段操作线交于点d
(2)原料为液化率等于 1/3 的气液混合物。 已知数据如下:操作条件下苯的气化潜热为 389kJ/kg,甲苯的气化潜热为 360kJ/kg。苯—甲苯混合液的气液平衡数据及 t-x-y 图见例 6-1 和图 解:(1)温度为 20℃的冷液进料 ①利用平衡数据,在直角坐标图上 绘平衡曲线及对角线,如本例附图 1 所示。在图上定出点 a(xD,xD)、 点 e(xF,xF)和点 c(xW,xW)三 点。 ② ,在 y 轴上定出点 b。联 ab,即得 到精馏段操作线。 ③先按下法计算 q 值。原料液的气化潜热为: 由图查出进料组成 时溶液的泡点为 93℃, 。由附录查得在 56.5℃下苯和甲苯的比热为 1.84kJ/(kg·℃),故原料液的平均比热为: 所以: 再从点 e 作斜率为 3.76 的直线,即得 q 线与精馏段操作线交于点 d
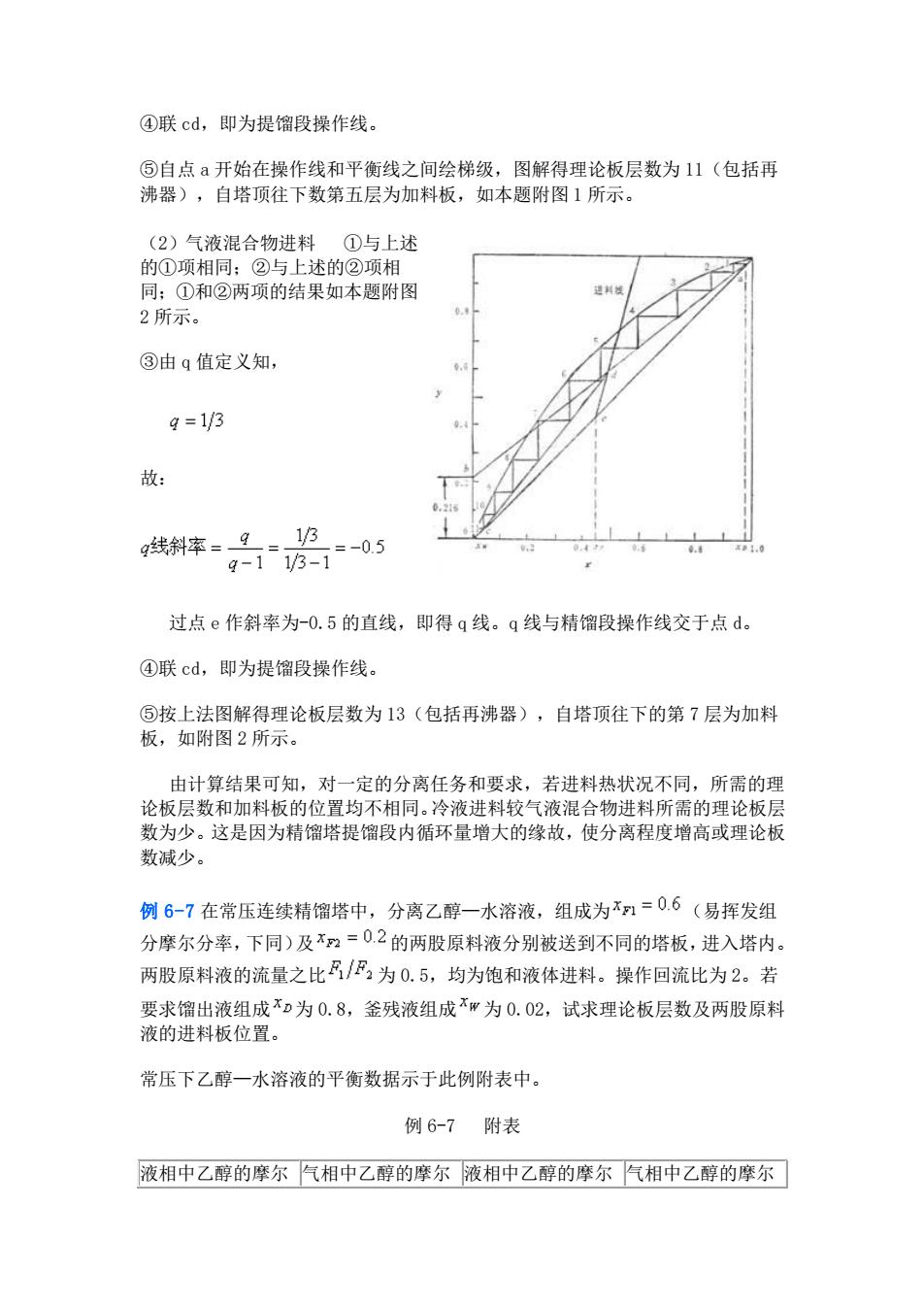
④联cd,即为提馏段操作线。 ⑤自点a开始在操作线和平衡线之间绘梯级,图解得理论板层数为11(包括再 沸器),自塔顶往下数第五层为加料板,如本题附图1所示。 (2)气液混合物进料①与上述 的①项相同:②与上述的②项相 同:①和②两项的结果如本题附图 2所示 ③由q值定义知 g=1/3 故: 线斜率=g品-05 13 过点e作斜率为-0.5的直线,即得q线。q线与精馏段操作线交于点d。 ④联cd,即为提馏段操作线。 ⑤按上法图解得理论板层数为13(包括再沸器),自塔顶往下的第7层为加料 板,如附图2所示 由计算结果可知,对一定的分离任务和要求,若进料热状况不同,所需的理 论板层数和加料板的位置均不相同。冷液进料较气液混合物进料所需的理论板层 数为少。这是因为精馏塔提馏段内循环量增大的缘故,使分离程度增高或理论板 数减少。 例6-7在常压连续精馏塔中,分离乙醇一水溶液,组成为x=0.6(易挥发组 分摩尔分率,下同)及=02的两股原料液分别被送到不同的塔板,进入塔内。 两股原料液的流量之比/风为0.5,均为饱和液体进料。操作回流比为2。若 要求馏出液组成不D为0.8,釜残液组成不"为0.02,试求理论板层数及两股原料 液的进料板位置。 常压下乙醇一水溶液的平衡数据示于此例附表中。 例6-7附表 液相中乙醇的摩尔气相中乙醇的摩尔液相中乙醇的摩尔气相中乙醇的摩尔
④联 cd,即为提馏段操作线。 ⑤自点 a 开始在操作线和平衡线之间绘梯级,图解得理论板层数为 11(包括再 沸器),自塔顶往下数第五层为加料板,如本题附图 1 所示。 (2)气液混合物进料 ①与上述 的①项相同;②与上述的②项相 同;①和②两项的结果如本题附图 2 所示。 ③由 q 值定义知, 故: 过点 e 作斜率为-0.5 的直线,即得 q 线。q 线与精馏段操作线交于点 d。 ④联 cd,即为提馏段操作线。 ⑤按上法图解得理论板层数为 13(包括再沸器),自塔顶往下的第 7 层为加料 板,如附图 2 所示。 由计算结果可知,对一定的分离任务和要求,若进料热状况不同,所需的理 论板层数和加料板的位置均不相同。冷液进料较气液混合物进料所需的理论板层 数为少。这是因为精馏塔提馏段内循环量增大的缘故,使分离程度增高或理论板 数减少。 例 6-7 在常压连续精馏塔中,分离乙醇—水溶液,组成为 (易挥发组 分摩尔分率,下同)及 的两股原料液分别被送到不同的塔板,进入塔内。 两股原料液的流量之比 为 0.5,均为饱和液体进料。操作回流比为 2。若 要求馏出液组成 为 0.8,釜残液组成 为 0.02,试求理论板层数及两股原料 液的进料板位置。 常压下乙醇—水溶液的平衡数据示于此例附表中。 例 6-7 附表 液相中乙醇的摩尔 气相中乙醇的摩尔 液相中乙醇的摩尔 气相中乙醇的摩尔

分率 分率 分率 分率 0. 0.0 0.45 0.635 0.01 0.11 0.50 0.657 0.02 0.175 0.55 0.678 0.04 0.275 0.60 0.698 0.06 0.340 0.65 0.725 0.08 0.392 0.70 0.755 0.10 0.430 0.75 0.785 0.14 0.482 0.80 0.820 0.18 0.513 0.85 0.855 0.20 0.525 0.894 0.894 0.25 0.551 0.90 0.898 0.30 0.575 0.95 0.942 0.35 0.595 1.0 1.0 0.40 0.614 解:如本例附图1所示,由于有两股进料,故全塔可分为三段。组成为的原 料液从塔较上部位的某加料板引入,该加料板以上塔段的操作线方程与无侧线塔 的精榴段操作线方程相同,即: =R+i+R中和(a 该操作线在y轴上的截距为: 0.8 -020
分率 分率 分率 分率 0.0 0.01 0.02 0.04 0.06 0.08 0.10 0.14 0.18 0.20 0.25 0.30 0.35 0.40 0.0 0.11 0.175 0.273 0.340 0.392 0.430 0.482 0.513 0.525 0.551 0.575 0.595 0.614 0.45 0.50 0.55 0.60 0.65 0.70 0.75 0.80 0.85 0.894 0.90 0.95 1.0 0.635 0.657 0.678 0.698 0.725 0.755 0.785 0.820 0.855 0.894 0.898 0.942 1.0 解:如本例附图 1 所示,由于有两股进料,故全塔可分为三段。组成为 的原 料液从塔较上部位的某加料板引入,该加料板以上塔段的操作线方程与无侧线塔 的精馏段操作线方程相同,即: (a) 该操作线在 y 轴上的截距为:

求得,即: 总物料: +R=L"+D(b) IF.Ir 易挥发组分 F:.In r1+耳x1=Lx,+DxD 式中”一一两股进料之间各层板的 上升蒸气流量,kmol/h: L“一一两股进料之间各层板的下降 液体流量,kmol/h: (下标s、s+1为两股进料之间各层板的序号) 由式(c)可得: -片5+m (d) 因进料为饱和液体,故=V=(R+D,L=L+R,则: +品+ L+R (R+1D(e) 式d及式e为两股进料之间塔段的操作线方程,也是直线方程式,它在y轴 上的截距为(Dx,-RxMR+)D。其中D可由物料衡算求得。 100=00kmol/ 设8=100malh,则3=05 对全塔作总物料及易挥发组分的衡算,得: 耳+=D+W=300,风x7+Rxm=DxD+Wxw 或0.6×100+0.2×200=0.8D+0.02w
两股进料板之间塔段的操作线方 程,可按图中虚线范围内作物料衡算 求得,即: 总物料: (b) 易挥发组分: 式中 ——两股进料之间各层板的 上升蒸气流量,kmol/h; ——两股进料之间各层板的下降 液体流量,kmol/h。 (下标 s、s+1 为两股进料之间各层板的序号) 由式(c)可得: (d) 因进料为饱和液体,故 , ,则: (e) 式 d 及式 e 为两股进料之间塔段的操作线方程,也是直线方程式,它在 y 轴 上的截距为 。其中 D 可由物料衡算求得。 设 ,则 对全塔作总物料及易挥发组分的衡算,得: , 或
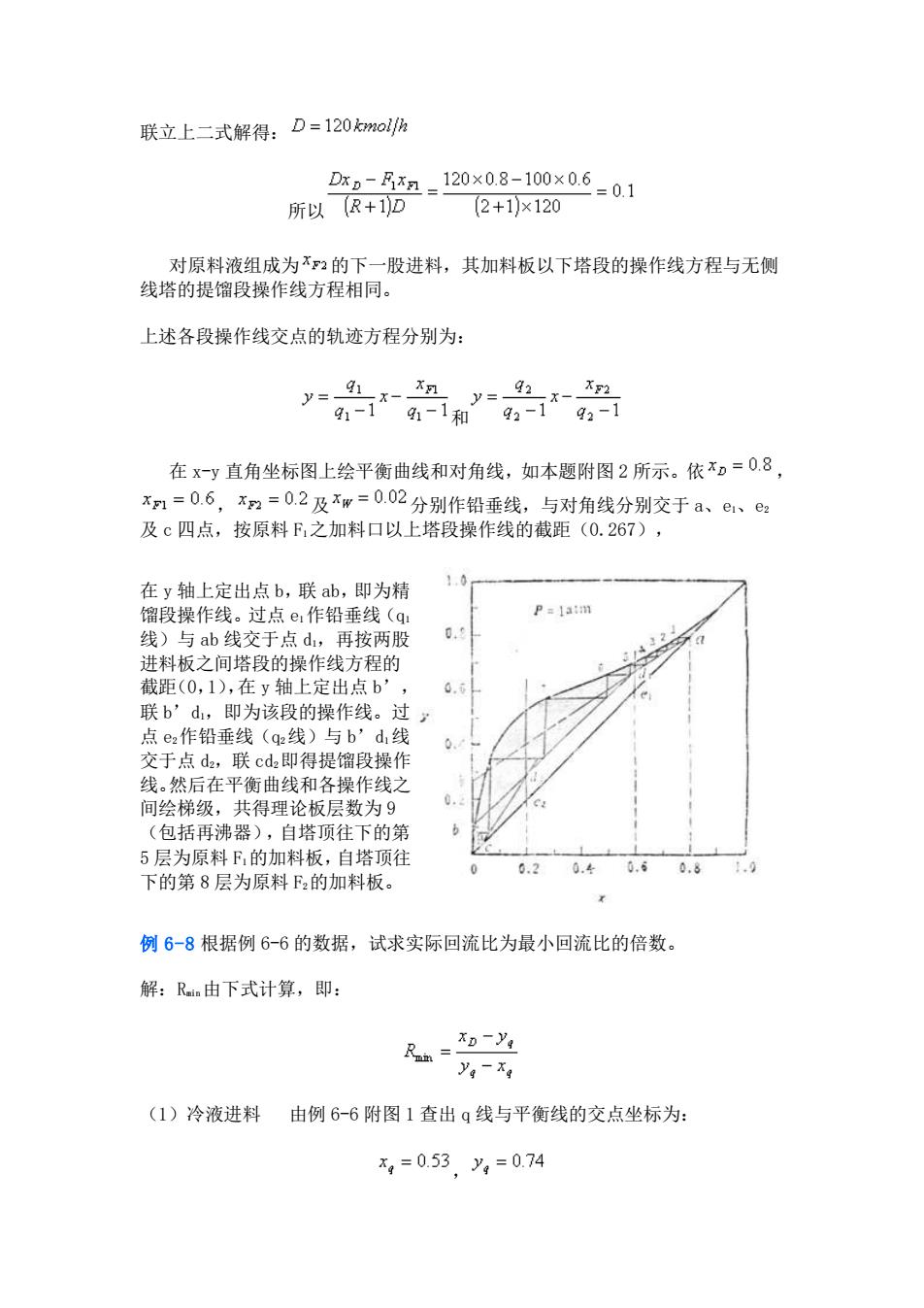
联立上二式解得:D=120olh Dx-Rxa-120×08-100×06-0.1 所以R+1D 2+1)×120 对原料液组成为不?的下一股进料,其加料板以下塔段的操作线方程与无侧 线塔的提馏段操作线方程相同。 上述各段操作线交点的轨迹方程分别为: 品品品品 91 在xy直角坐标图上绘平衡曲线和对角线,如本题附图2所示。依D=0.8, x1=0.6,xm=0.2及不w=0.02分别作铅垂线,与对角线分别交于a、1、2 及c四点,按原料,之加料口以上塔段操作线的截距(0.267), 在y轴上定出点b,联ab,即为精 10 馏段操作线。过点e作铅垂线(a Pa 1atm 线 ab线交于点d,再按两股 e 进料板之间塔段的操作线方程的 截距(0,1),在y轴上定出点b’, 联b’d,即为该段的操作线。过 线。然后在平衡曲线和各操作线之 间绘梯级,共得理论板层数为9 (包括再沸器),自塔顶往下的第 5层为原料F,的加料板,自塔顶往 6.20.40,60.8 下的第8层为原料F,的加料板 例6-8根据例6-6的数据,试求实际回流比为最小回流比的倍数。 解:Rn由下式计算,即: R-0当 yo-x4 (1)冷液进料由例6-6附图1查出g线与平衡线的交点坐标为: x,=053.yg=0.74
联立上二式解得: 所以 对原料液组成为 的下一股进料,其加料板以下塔段的操作线方程与无侧 线塔的提馏段操作线方程相同。 上述各段操作线交点的轨迹方程分别为: 和 在 x-y 直角坐标图上绘平衡曲线和对角线,如本题附图 2 所示。依 , , 及 分别作铅垂线,与对角线分别交于 a、e1、e2 及 c 四点,按原料 F1之加料口以上塔段操作线的截距(0.267), 在 y 轴上定出点 b,联 ab,即为精 馏段操作线。过点 e1作铅垂线(q1 线)与 ab 线交于点 d1,再按两股 进料板之间塔段的操作线方程的 截距(0,1),在 y 轴上定出点 b’, 联 b’d1,即为该段的操作线。过 点 e2作铅垂线(q2线)与 b’d1线 交于点 d2,联 cd2即得提馏段操作 线。然后在平衡曲线和各操作线之 间绘梯级,共得理论板层数为 9 (包括再沸器),自塔顶往下的第 5 层为原料 F1的加料板,自塔顶往 下的第 8 层为原料 F2的加料板。 例 6-8 根据例 6-6 的数据,试求实际回流比为最小回流比的倍数。 解:Rmin由下式计算,即: (1)冷液进料 由例 6-6 附图 1 查出 q 线与平衡线的交点坐标为: