
内容 国国 、1958 一、红外光谱法的基本原理 ◆二、红外分光光度计 ◆三、红外光谱与分子结构的关系 ◆四、红外谱图解析般步骤
内 容 一、红外光谱法的基本原理 二、红外分光光度计 三、红外光谱与分子结构的关系 四、红外谱图解析一般步骤
红外光谱的概述 红外光谱:系指2.5-25um之间的吸收光谱,分子中基团的振动 和转动能级跃迁产生的:振-转光谱。 光辐射→分子振动能级跃迁红外吸收光谱官能团→分子结构 频率V 能量 低 化学锭断裂 电子跃迁 据动旺迁 性动氏年原子饺自特青轻 无线 x射线 紫外 红外 微波 电波 区 IR R 紫外 可见 振动红外 核磁共振 400036003200280024002000180016001t0012001000800600 200nm 400nm 800nm2.5l 15μ ()仲丁醇的红外光 短 波长入 长 光波谱区及能量跃迁相关图
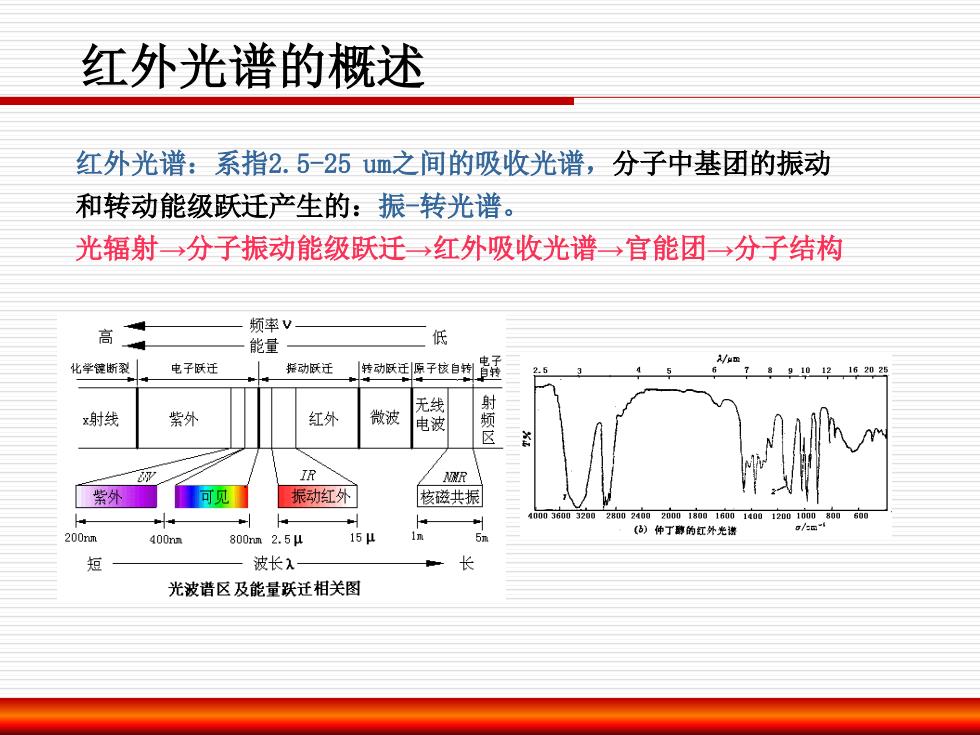
红外光谱:系指2.5-25 um之间的吸收光谱,分子中基团的振动 和转动能级跃迁产生的:振-转光谱。 光辐射→分子振动能级跃迁→红外吸收光谱→官能团→分子结构 红外光谱的概述

双原子分子的能级跃迁示意图 1 V"=0 E2 3 纯电子 跃迁 ”=0 6 4 纯转动 纯振动 2 低迁 跃迁 V=0 双原子分子的三种能级跃迁示意图 =0 谐振子()及非谐振子(b)的势能曲线
双原子分子的能级跃迁示意图
红外光谱 红外光谱图:当用一束具有连续波长红外光照射物质时,该物质的分子 就会吸收一定波长的红外光的光能,并转化为分子的振动能量和转动能 量。以波长或波数为为横坐标,以百分透过率或吸收率为纵坐标,记录 其吸收曲线,即得到该物质的红外吸收光谱。 红外光谱图:纵坐标为吸收强度或透过率,横坐标为波长(2u)或 波数1/2单位:cm,波长和波数的关系: ◆v(cm-)=104nμm, ◆红外光谱图可以用峰数,峰位,峰形,蜂强来描述。 40003000.2500 2400 15001301100100090e800 70650 60 40 680 2.5 101112131415
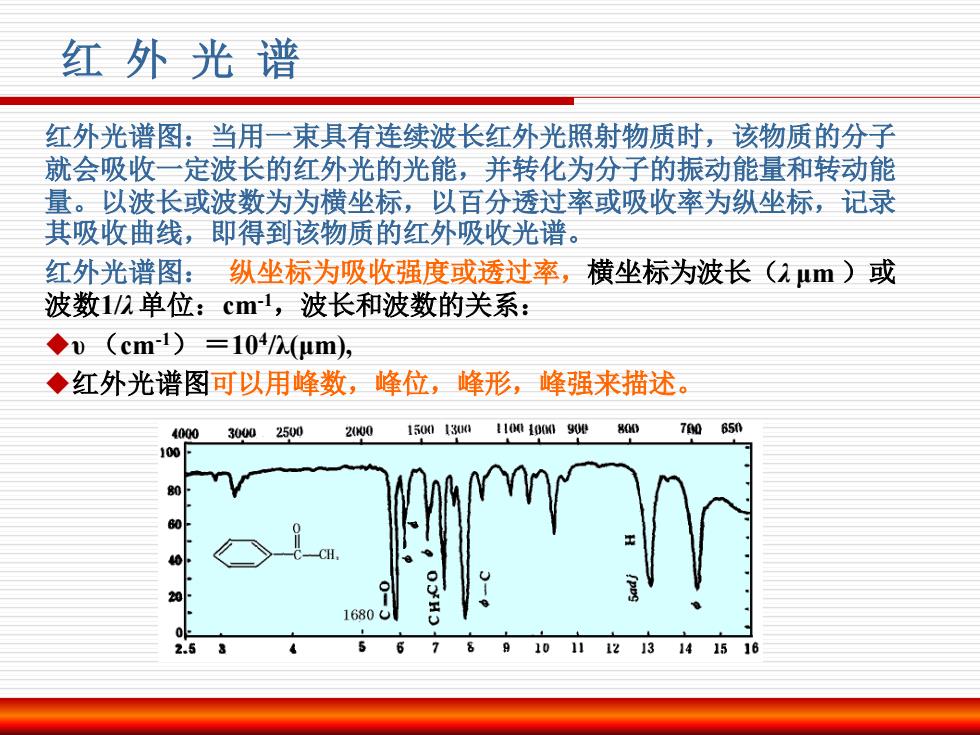
红 外 光 谱 红外光谱图:当用一束具有连续波长红外光照射物质时,该物质的分子 就会吸收一定波长的红外光的光能,并转化为分子的振动能量和转动能 量。以波长或波数为为横坐标,以百分透过率或吸收率为纵坐标,记录 其吸收曲线,即得到该物质的红外吸收光谱。 红外光谱图: 纵坐标为吸收强度或透过率,横坐标为波长(λ μm )或 波数1/λ单位:cm-1,波长和波数的关系: υ (cm-1) =104 /λ(μm), 红外光谱图可以用峰数,峰位,峰形,峰强来描述
红外光谱法的划分及特点 红外区的划分 区域 入/um o/cm-1 能级跃迁类型 近红外区 0.752.5 133004000 主要用于研究O一H、N一H、C H键的的倍频和组合频吸收 中红外区 2.525 4000400 振动的基频 远红外区 25~1000 400~10 骨架振动和转动,晶格振动 红外光谱的特点: 1可以鉴定未知物分子结构或确定其化学基团 2固体、气体、液体样品都可以直接测定。对一些表面涂层和不溶 、不熔融的弹性体也可直接测得其红外光谱 3样品用量少,不破坏试样,分析速度快,操作方便
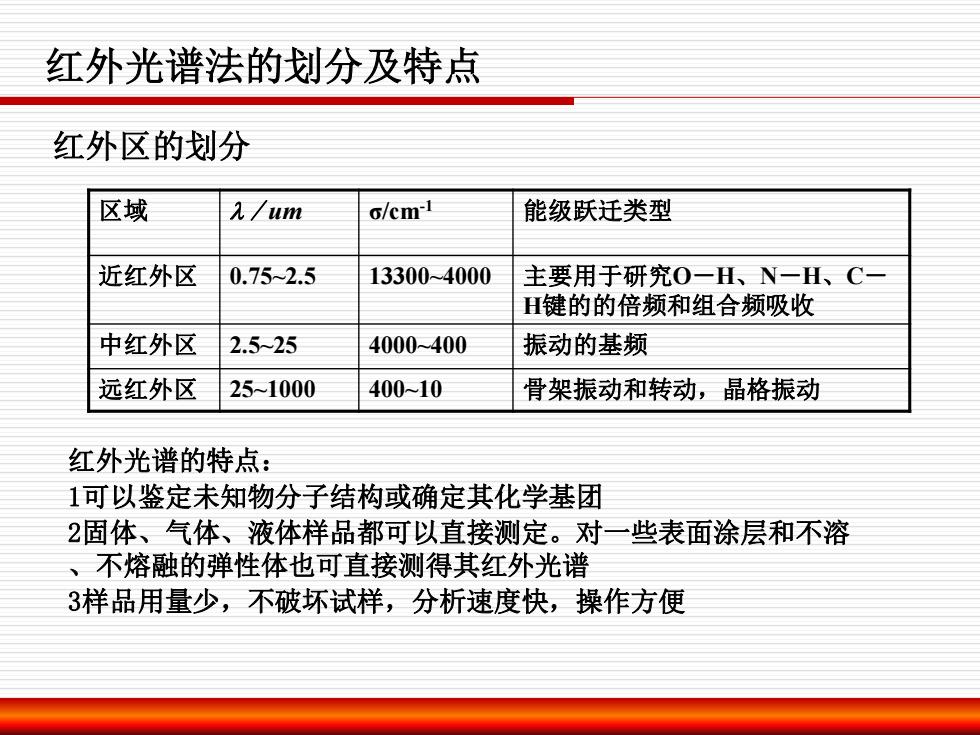
红外光谱法的划分及特点 区域 /um σ/cm-1 能级跃迁类型 近红外区 0.75~2.5 13300~4000 主要用于研究O-H、N-H、C- H键的的倍频和组合频吸收 中红外区 2.5~25 4000~400 振动的基频 远红外区 25~1000 400~10 骨架振动和转动,晶格振动 红外区的划分 红外光谱的特点: 1可以鉴定未知物分子结构或确定其化学基团 2固体、气体、液体样品都可以直接测定。对一些表面涂层和不溶 、不熔融的弹性体也可直接测得其红外光谱 3样品用量少,不破坏试样,分析速度快,操作方便

、 红外光谱法的基本原理 (一)红外光谱产生的条件 红外光谱是由分子振动能级的跃迁而产生,但并不是所有的振 动能级的跃迁都能在红外光谱中产生吸收,物质吸收红外光发生振 动和转动能级跃迁必须满足两个条件: 1.辐射应具有能满足物质产生振动跃迁所需的能量; 2.分子振动时偶极矩的大小和方向必须有一定的变化,即具有偶极矩 变化的分子振动是红外活性振动。 对称分子:没有偶极矩,辐射不能引起共振,无红外活性。如:N? 、02、Cl2等。 非对称分子:有偶极矩,红外活性,水分子,H,O,NH
一、红外光谱法的基本原理 。 红外光谱是由分子振动能级的跃迁而产生,但并不是所有的振 动能级的跃迁都能在红外光谱中产生吸收,物质吸收红外光发生振 动和转动能级跃迁必须满足两个条件: 1.辐射应具有能满足物质产生振动跃迁所需的能量; 2.分子振动时偶极矩的大小和方向必须有一定的变化,即具有偶极矩 变化的分子振动是红外活性振动。 对称分子:没有偶极矩,辐射不能引起共振,无红外活性。 如:N2 、O2、Cl2 等。 非对称分子:有偶极矩,红外活性,水分子,H2O,NH3 (一)红外光谱产生的条件

(二)分子振动频率方程式 1.双原子分子的简谐振动及其频率 ●一00-一● 分子是由各种原子以化学键相互连接而成,以双原子 ●-0000000000000-◆ 分子为例,将分子看作一个简单的谐振子,假设化学 键为失重弹簧,化学键的振动类似于连接两个小球的弹簧,根据经 典力学原理,简谐振动遵循虎克定律。双原子分子只有沿化学键的 一种振动方式,当分子振动时,化学键的电荷分布发生改变,若两 个原子不同,分子的电荷中心于两个原子核同步振荡,分子仿佛二 个振荡的电偶极子,当偶极受到连续波长的红外光照射时,分子可 吸收某些波长的红外光从而增大分子的振动能量,所吸收的红外光 的频率与该分子的振动能级一致。 ●-一0000-· 虎克足律 1 -0000000000000-● V= k 2π M
(二)分子振动频率方程式 1.双原子分子的简谐振动及其频率 分子是由各种原子以化学键相互连接而成,以双原子 分子为例,将分子看作一个简单的谐振子,假设化学 键为失重弹簧,化学键的振动类似于连接两个小球的弹簧,根据经 典力学原理,简谐振动遵循虎克定律。双原子分子只有沿化学键的 一种振动方式,当分子振动时,化学键的电荷分布发生改变,若两 个原子不同,分子的电荷中心于两个原子核同步振荡,分子仿佛一 个振荡的电偶极子,当偶极受到连续波长的红外光照射时,分子可 吸收某些波长的红外光从而增大分子的振动能量,所吸收的红外光 的频率与该分子的振动能级一致

(二)分子振动频率方程式 分子的振动能级(量子化):E振=(V+1/2)hv V:化学键的振动频率;v:振动量子数(v=0,1,2,3.。) 任意两个相邻的能级间的能量差头4E=加=会臣 K化学键的力常数,与键能和键长有)v=,1 4二m1m2 2πJu 01十m2 为双原子的折合质量=mml(m+m2) 发生振动能级跃迁需要能量的大小取决手键两端原子的折合质量 和键的力常数,即取决于分子的结构特征 化学键键能越强(即键的力常数越大)原子折合质量越小,化 学键的振动频率越大,吸收峰将出现在高波数区
(二)分子振动频率方程式 分子的振动能级(量子化): E振=(V+1/2)h V :化学键的振动频率; :振动量子数(v=0,1,2,3…。) 任意两个相邻的能级间的能量差为: K化学键的力常数,与键能和键长有关, 为双原子的折合质量=m1m2 /(m1+m2) 发生振动能级跃迁需要能量的大小取决于键两端原子的折合质量 和键的力常数,即取决于分子的结构特征 化学键键能越强(即键的力常数K越大)原子折合质量越小,化 学键的振动频率越大,吸收峰将出现在高波数区

(二)分子振动频率方程式 某些键的伸缩力常数(毫达因埃) 键 分子 k 键 分子 k H-F HF 9.7 H-C CH2-CH2 5.1 4.8 H-c C-C,C-N,C-O键力常数相近,原 H-C1 I CH≡CH 5.9 4.1 C-CI CHaCl 3.4 子折合质量不同, C-C 4.5w5.6 H-0 H20 C-C 9.5m9.9 HzS 4.3 C=C 15~17 其大小顺序为:C-C《CN〈C-O NHz 6.5 C-0 12w13 H-C CHsX 4.7m5.0 C=0 16w18 键类型 -C=C一 -C=C- > -C-C= 力常数 15~17 9.59.9 4.5~5.6 峰位 2200cm-1 1640cm-1 1300cm-1 化学键键能越强(即键的力常数K越大)原子折合质量越小,化学键的振动 频率越大,吸收峰将出现在高波数区。 例题:由表中查知C=C键的K=9.5~9.9,令其为9.6,计算波数值 可=-2cJ臣=107√ -=1307J 9.6 12/2 =1653cm1 正己烯中C=C键伸缩振动频率实测值为1652cml
某些键的伸缩力常数(毫达因/埃) 化学键键能越强(即键的力常数K越大)原子折合质量越小,化学键的振动 频率越大,吸收峰将出现在高波数区。 例题: 由表中查知C=C键的K=9.5 9.9 ,令其为9.6, 计算波数值 正己烯中C=C键伸缩振动频率实测值为1652 cm-1 C-C,C-N,C-O键力常数相近,原 子折合质量不同, 其大小顺序为:C-C《C-N〈C-O (二)分子振动频率方程式 键类型 —CC — > —C =C — > —C — C — 力常数 15 17 9.5 9.9 4.5 5.6 峰位 2200cm-1 1640 cm-1 1300 cm-1
(三)分子中基团的基本振动形式 1.两类基本振动形式 亚甲基伸缩振动: 伸缩振动:指化学键两端的原子沿键轴方向 作来回周期伸缩运动,键长发生变化而键角 不变,它又可分为对称与非对称伸缩 变形振动:原子垂直与价键方向的运动,基 团键角发生周期变化而键长不变,包括剪式 对称伸缩振动反对称伸缩振动 振动、平面摇摆、非平面摇摆以及扭曲振动。 0s:2853cm104s:2926:cm1 (强吸收S) 亚甲基变形振动 摇摆(面外)扭曲 剪式(面内)摇摆 v:1306-1303cm1T:1250cm1δ:1468cm1p:720cm1 (弱吸收) (中等吸收M)
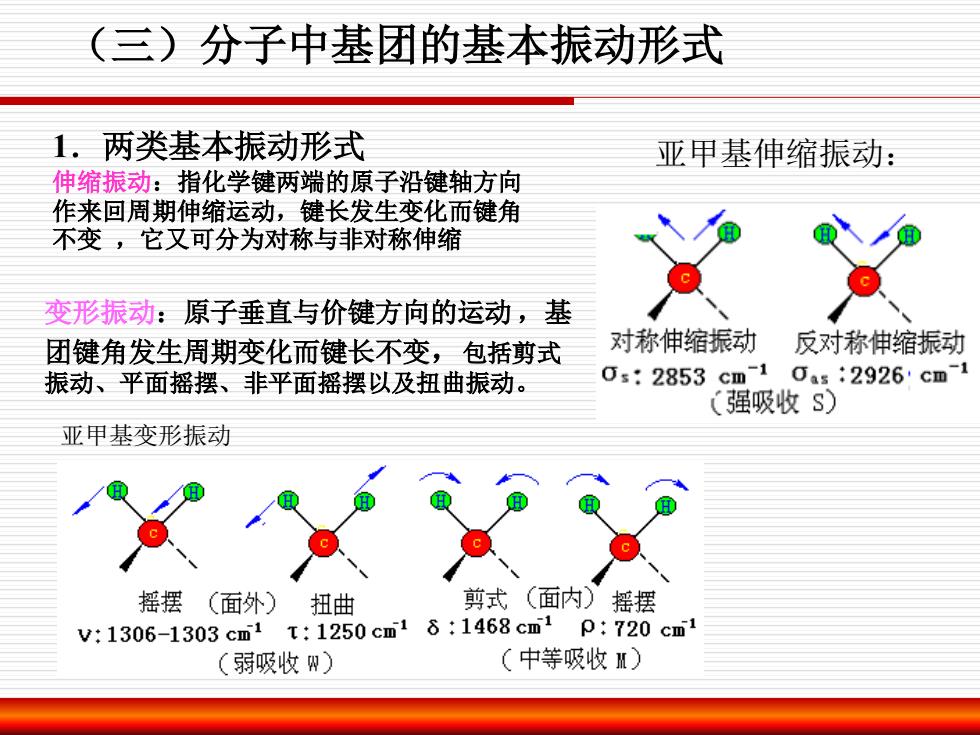
(三)分子中基团的基本振动形式 1.两类基本振动形式 伸缩振动:指化学键两端的原子沿键轴方向 作来回周期伸缩运动,键长发生变化而键角 不变 ,它又可分为对称与非对称伸缩 变形振动:原子垂直与价键方向的运动 ,基 团键角发生周期变化而键长不变,包括剪式 振动、平面摇摆、非平面摇摆以及扭曲振动。 亚甲基伸缩振动: 亚甲基变形振动