
第8卷第6期 智能系统学报 Vol.8 No.6 2013年12月 CAAI Transactions on Intelligent Systems Dec.2013 D0:10.3969/j.issn.1673-4785.201306035 网络出版地址:http://www.enki..net/kcms/detail/23.1538.TP.20131012.1814.007.html 基于小波HMM的UUV传感器数据孤立点检测 移岩,侯怒萍2,迟冬南 (1.海军驻沈阳地区舰船配套军事代表室,辽宁沈阳110031;2.哈尔滨工程大学机电工程学院,黑龙江哈尔滨 150001;3.哈尔滨工程大学自动化工程学院,黑龙江哈尔滨150001) 摘要:针对水下无人潜航器(UV)预测跟踪过程中传感器所采集数据的不准确问题,提出了一种利用小波隐马尔 可夫模型进行UUV预测跟踪数据孤立点检测的方法利用改进递归小波变换,对原始数据进行重构,小波系数中孤 立点处的系数得到局部放大小波系数的更新基于历史时刻的数据,因此,可以利用正常数据与孤立点的差异对数据 进行实时处理利用隐马尔可夫模型定义异常值分布判定函数,并以其作为依据,检测特征明显异于正常数据的孤立 点将准孤立点利用惰性算法进行重检测,提高孤立点检测的准确性.湖试数据验证了该方法能够有效地检测出UUV 预测跟踪中的数据孤立点. 关键词:水下无人潜航器:预测跟踪:小波变换:隐马尔可夫;孤立点检测 中图分类号:TP18:TN96711文献标志码:A文章编号:1673-4785(2013)06-0551-07 中文引用格式:穆岩,侯恕萍,迟冬南.基于小波HMM的UUV传感器数据孤立点检测[J].智能系统学报,2013,8(6):551-557. 英文引用格式:MU Yan,HOU Shuping,CHI Dongnan.UUV sensor data outlier detection using wavelet HMM[J].CAAI Transac- tions on Intelligent Systems,2013,8(6):551-557. UUV sensor data outlier detection on the basis of wavelet HMM MU Yan',HOU Shuping',CHI Dongnan? (1.Representative Department for Forming Complete Sets of Naval Ships in the Area of Shenyang,Shenyang 110031,China;2.Col- lege of Mechanical and Electrical Engineering,Harbin Engineering University,Harbin 150001,China;3.College of Aotomation,Har- bin Engineering University,Harbin 150001,China) Abstract:A method for outlier detection based on wavelet HMM hidden Markov model)is proposed in this paper in order to deal with the inaccurate original data collected from sensors during UUV forecast tracing.The improved recursive wavelet transform (IRWT)is used to reconstruct the original data and locally amplify the wavelet coeffi- cients of the outliers.The update of wavelet coefficients are based on the data at the historical moment,thus,data may be processed in real time by utilizing the difference between normal data and outliers.The judgment function on the distribution of abnormal values is defined by HMM.In addition,on the basis of this,the outliers with features obviously different from the normal data are detected.The quasi-outliers are redetected by using a lazy algorithm for improving the accuracy of the detection results.The data from the lake experiment verify that the method may effec- tively detect the data outliers in UUV forecast tracing. Keywords:underwater unmanned vehicle;forecast tracing;wavelet transform;hidden Markov model;outlier de- tection UUV(underwater unmanned vehicle)的预测跟踪 主要应用于其在未知环境中航行、对环境进行感知 并完成既定任务的过程中在感知未知环境的过程 收稿日期:2013-06-20.网络出版日期:2013-10-12 中,传感器所采集的数据成为UUV自主决策的惟一 基金项目:国家自然科学基金资助项目(51109043). 通信作者:侯恕萍.E-mail:houshuping@hrbeu.cdu.cn 依据.因此,原始数据的准确性直接影响着UUV的
第 8 卷第 6 期 智 能 系 统 学 报 Vol.8 №.6 2013 年 12 月 CAAI Transactions on Intelligent Systems Dec. 2013 DOI:10.3969 / j.issn.1673⁃4785.201306035 网络出版地址:http: / / www.cnki.net / kcms/ detail / 23.1538.TP.20131012.1814.007.html 基于小波 HMM 的 UUV 传感器数据孤立点检测 穆岩1 ,侯恕萍2 ,迟冬南3 (1.海军驻沈阳地区舰船配套军事代表室,辽宁 沈阳 110031; 2. 哈尔滨工程大学 机电工程学院,黑龙江 哈尔滨 150001; 3. 哈尔滨工程大学 自动化工程学院,黑龙江 哈尔滨 150001) 摘 要:针对水下无人潜航器(UUV)预测跟踪过程中传感器所采集数据的不准确问题,提出了一种利用小波隐马尔 可夫模型进行 UUV 预测跟踪数据孤立点检测的方法.利用改进递归小波变换,对原始数据进行重构,小波系数中孤 立点处的系数得到局部放大.小波系数的更新基于历史时刻的数据,因此,可以利用正常数据与孤立点的差异对数据 进行实时处理.利用隐马尔可夫模型定义异常值分布判定函数,并以其作为依据,检测特征明显异于正常数据的孤立 点.将准孤立点利用惰性算法进行重检测,提高孤立点检测的准确性.湖试数据验证了该方法能够有效地检测出 UUV 预测跟踪中的数据孤立点. 关键词:水下无人潜航器;预测跟踪;小波变换;隐马尔可夫;孤立点检测 中图分类号: TP18;TN96711 文献标志码:A 文章编号:1673⁃4785(2013)06⁃0551⁃07 中文引用格式:穆岩,侯恕萍,迟冬南. 基于小波 HMM 的 UUV 传感器数据孤立点检测[J]. 智能系统学报, 2013, 8(6): 551⁃557. 英文引用格式:MU Yan,HOU Shuping, CHI Dongnan. UUV sensor data outlier detection using wavelet HMM[J]. CAAI Transac⁃ tions on Intelligent Systems, 2013, 8(6): 551⁃557. UUV sensor data outlier detection on the basis of wavelet HMM MU Yan 1 , HOU Shuping 2 , CHI Dongnan 3 (1. Representative Department for Forming Complete Sets of Naval Ships in the Area of Shenyang, Shenyang 110031, China; 2. Col⁃ lege of Mechanical and Electrical Engineering, Harbin Engineering University, Harbin 150001, China; 3. College of Aotomation, Har⁃ bin Engineering University, Harbin 150001, China) Abstract:A method for outlier detection based on wavelet HMM (hidden Markov model) is proposed in this paper in order to deal with the inaccurate original data collected from sensors during UUV forecast tracing. The improved recursive wavelet transform (IRWT) is used to reconstruct the original data and locally amplify the wavelet coeffi⁃ cients of the outliers. The update of wavelet coefficients are based on the data at the historical moment, thus, data may be processed in real time by utilizing the difference between normal data and outliers. The judgment function on the distribution of abnormal values is defined by HMM. In addition, on the basis of this, the outliers with features obviously different from the normal data are detected. The quasi-outliers are redetected by using a lazy algorithm for improving the accuracy of the detection results. The data from the lake experiment verify that the method may effec⁃ tively detect the data outliers in UUV forecast tracing. Keywords: underwater unmanned vehicle; forecast tracing; wavelet transform; hidden Markov model; outlier de⁃ tection 收稿日期:2013⁃06⁃20. 网络出版日期:2013⁃10⁃12. 基金项目:国家自然科学基金资助项目(51109043). 通信作者:侯恕萍. E⁃mail:houshuping@ hrbeu.edu.cn. UUV(underwater unmanned vehicle)的预测跟踪 主要应用于其在未知环境中航行、对环境进行感知 并完成既定任务的过程中.在感知未知环境的过程 中,传感器所采集的数据成为 UUV 自主决策的惟一 依据.因此,原始数据的准确性直接影响着 UUV 的

.552. 智能系统学报 第8卷 预测跟踪效果及任务完成的效率,甚至关系着UUV 实时预测跟踪的目的.文中所提出的算法流程如图1 自身的安全。 所示。 由于环境噪声等因素的影响,在传感器采集的 (开始● 原始数据中存在噪声点,即特征明显异于正常数据 提取原始数据 的孤立点.小波转换可以重构原始数据,将其中的孤 立点局部放大,使得孤立点的检测及剔除都更加准 小波变换 确.文献[1]将改进递归小波引入到瞬时故障信号的 HMM相似度判定 实时分析过程中,选择衰减振荡函数为基波,用信号 Y是香相似一 和经过转换、量化后基波间的相似性表示小波转换: N 放人备选集R 并将小波变换后的数据孤立点局部放大,对其进行 检测,即可得到有效数据. 预测小波系数 由于传感器探测数据属于随机过程,所以考虑 判断预测 用随机过程的相关理论进行孤立点检测.马尔可夫 系数与原始数据是否 W 有明显波动 随机过程的核心思想是无后效性,即当前时刻的状 孤立点 正常数据■ 态变量与之前更早时刻的状态变量无关,而只与其 Num+1 前一时刻的状态变量相关,这种模型结构某种程度 上反映了事物发展的过程.隐马尔可夫随机过程相 是否达到数据总数Num> 对于马尔可夫随机过程来说,主要特征是状态变量 Y 结束○ 的隐藏性.马尔可夫和隐马尔可夫过程广泛应用于 预测和隐含概念漂移的数据流分类中[).文献[3] 图1算法流程 Fig.1 Flow chart of the algorithm 针对隐马尔可夫模型传统训练算法易收敛于局部极 值的问题,提出一种带极值扰动的自适应调整惯性 在UUV预测跟踪过程中,传感器所采集的信号 权重和加速系数的粒子群算法,将改进后的粒子群 包括速度、航向、深度及声呐所采集的避碰信息.在 优化算法引入到隐马尔可夫模型的训练中,分别对 所采集的数据中,由于传感器自身的特性以及外界 隐马尔可夫模型的状态数和参数进行优化.提出的 环境的影响,存在异常数据的情况.这些异常数据对 基于改进粒子群优化算法的隐马尔可夫模型训练算 于UUV预测跟踪的准确性及安全性有着至关重要 法与传统隐马尔可夫模型训练算法Baum-welch算 的影响所以,对异常数据的实时处理,成为UUV预 法相比,能有效地跳出局部极值,从而使训练后的隐 测跟踪过程中必不可少的环节.基于这一实际的需 马尔可夫模型具有较好的识别能力。 求,本文利用小波变换将异常数据和正常数据进行 文献[4]结合小波理论和隐马尔可夫模型的相 分离 关知识,将小波变换应用到隐马尔可夫模型非参数 对于采集所得的数据s(t)来说,其小波变换由 估计的问题中来,并探讨了其中Haar小波正交级数 系数集合W(b,a)组成,其中a为尺度因子,b为平 估计量分解尺度的选取.文中仅就小波理论和隐马 移因子,表示小波函数在t轴上的平移位置.小波系 尔可夫模型进行理论的结合,没有进行实验性的验 数W(b,a)为对数据s(t)和小波基函数(t)的卷 证.文献[5]针对小波异常信号检测原理的局限性, 积结果.卷积操作可以通过Z变换转换为乘积运算, 提出了适用于过程数据的基于小波隐马尔可夫模型 得到W(z),再对W,(z)进行Z反变换,得到小波系 的异常数据检测方法.将小波HMM相结合用于 数W(b,a) UUV预测跟踪过程中孤立点的实时检测,从理论方 小波系数W(b,a)的内积形式为 面考虑,这一应用具有可行性 w(6,a)=s0)·6山 1改进递归的小波变换 式中:山代表复共轭.根据容许条件c。= UUV预测跟踪过程中需要进行实时的数据支 (1(w)/小w)dw<o,选择小波基函数() 持,所提出的算法必须满足复杂度尽可能小的要求 本文利用改进递归的小波变换对原始数据进行重 的形式为 构,可以满足对算法复杂度的需求,进而实现UUV )=(1+o川+7r)ee
预测跟踪效果及任务完成的效率,甚至关系着 UUV 自身的安全. 由于环境噪声等因素的影响,在传感器采集的 原始数据中存在噪声点,即特征明显异于正常数据 的孤立点.小波转换可以重构原始数据,将其中的孤 立点局部放大,使得孤立点的检测及剔除都更加准 确.文献[1]将改进递归小波引入到瞬时故障信号的 实时分析过程中,选择衰减振荡函数为基波,用信号 和经过转换、量化后基波间的相似性表示小波转换; 并将小波变换后的数据孤立点局部放大,对其进行 检测,即可得到有效数据. 由于传感器探测数据属于随机过程,所以考虑 用随机过程的相关理论进行孤立点检测.马尔可夫 随机过程的核心思想是无后效性,即当前时刻的状 态变量与之前更早时刻的状态变量无关,而只与其 前一时刻的状态变量相关,这种模型结构某种程度 上反映了事物发展的过程.隐马尔可夫随机过程相 对于马尔可夫随机过程来说,主要特征是状态变量 的隐藏性.马尔可夫和隐马尔可夫过程广泛应用于 预测和隐含概念漂移的数据流分类中[2] .文献[3] 针对隐马尔可夫模型传统训练算法易收敛于局部极 值的问题,提出一种带极值扰动的自适应调整惯性 权重和加速系数的粒子群算法,将改进后的粒子群 优化算法引入到隐马尔可夫模型的训练中,分别对 隐马尔可夫模型的状态数和参数进行优化.提出的 基于改进粒子群优化算法的隐马尔可夫模型训练算 法与传统隐马尔可夫模型训练算法 Baum⁃welch 算 法相比,能有效地跳出局部极值,从而使训练后的隐 马尔可夫模型具有较好的识别能力. 文献[4]结合小波理论和隐马尔可夫模型的相 关知识,将小波变换应用到隐马尔可夫模型非参数 估计的问题中来,并探讨了其中 Haar 小波正交级数 估计量分解尺度的选取.文中仅就小波理论和隐马 尔可夫模型进行理论的结合,没有进行实验性的验 证.文献[5]针对小波异常信号检测原理的局限性, 提出了适用于过程数据的基于小波隐马尔可夫模型 的异常数据检测方法. 将小波 HMM 相结合用于 UUV 预测跟踪过程中孤立点的实时检测,从理论方 面考虑,这一应用具有可行性. 1 改进递归的小波变换 UUV 预测跟踪过程中需要进行实时的数据支 持,所提出的算法必须满足复杂度尽可能小的要求. 本文利用改进递归的小波变换对原始数据进行重 构,可以满足对算法复杂度的需求,进而实现 UUV 实时预测跟踪的目的.文中所提出的算法流程如图 1 所示. 图 1 算法流程 Fig.1 Flow chart of the algorithm 在 UUV 预测跟踪过程中,传感器所采集的信号 包括速度、航向、深度及声呐所采集的避碰信息.在 所采集的数据中,由于传感器自身的特性以及外界 环境的影响,存在异常数据的情况.这些异常数据对 于 UUV 预测跟踪的准确性及安全性有着至关重要 的影响.所以,对异常数据的实时处理,成为 UUV 预 测跟踪过程中必不可少的环节.基于这一实际的需 求,本文利用小波变换将异常数据和正常数据进行 分离. 对于采集所得的数据 s(t)来说,其小波变换由 系数集合 Ws(b,a) 组成,其中 a 为尺度因子, b 为平 移因子,表示小波函数在 t 轴上的平移位置.小波系 数 Ws(b,a) 为对数据 s(t)和小波基函数 ψ(t) 的卷 积结果.卷积操作可以通过 Z 变换转换为乘积运算, 得到 Ws(z) ,再对 Ws(z) 进行 Z 反变换,得到小波系 数 Ws(b,a) . 小波系数 Ws(b,a) 的内积形式为 Ws(b,a) = ∫ ¥ -¥ s(t)·ψ - b,a dt. 式 中: ψ - 代 表 复 共 轭. 根 据 容 许 条 件 cψ = ∫ ¥ -¥ ψ ^ (w) 2 ( / w ) dw < ¥,选择小波基函数 ψ(t) 的形式为 ψ(t) = (1 + σ t + σ 2 2 t 2 )e -σ t e iw0 t . ·552· 智 能 系 统 学 报 第 8 卷

第6期 穆岩,等:基于小波HMM的UUV传感器数据孤立点检测 ·553. 式中:山(地)为山(t)的傅里叶转换,其Z变换为 ag≥0, (z)= 6121+62z2+6323+64z4+6z U=1 入121+入222+23+42+25+26 利用马尔可夫链表示预测跟踪过程中小波变换 式中:e=ema-i0,A1=-66,A2=15e2,入3= 重构后的数据异常情况.将小波转换后的小波系数 -20e3,入4=158°,入5=-6e5,入6=6, 所表示的数据分为2种情况,即正常数据和异常数 8,=[(fT)3/3-(afT)/4+(fT)5/5]·6, 据,其中s1表示正常数据,5。表示异常数据.根据这 一划分标准,模型的状态变量总数N=2 62=[10(fT)3-25(gT)4+26(gT)]·e2/15, 状态和观测值之间的随机过程用观测值概率矩 8,=[66(σfT)3-30(σfT)3]·s3/15, 阵B=(ba)wxv描述.ba表示状态q,为s:时第k时刻 8,=[10(gfT)3+25(gT)4+26(fT)]·e/15, 小波系数W,(kT,)与正常数据小波系数W的相 δ5=[10(fT)3+5(fT)4+2(fT)3]·e3/30. 似率,观测概率矩阵元素和相似率分别为 则小波系数的Z变换形式为 bu P[W,W,(kTf)s=s;], W(z)=TF[s(z)·(z)]. (1) P[W,W.(kTf)s k]N[W.(kT f)w.W]= 式中:s(z)为数据s(t)的Z变换,T表示周期f表示 频率通过对式(1)进行Z反变换,可以得到小波系 exp-(W.(KT/)-w.)w(W.(T/)-w). 数表示如下: 式中:W[·|·]为正态分布,Wm为正常小波系数方差 由于隐马尔可夫过程的实质是当前时刻的状态 W,(kT,f)=fT{δs[(k-1)T,f月+δ2s· 只与其前一时刻的状态相关,因此,小波系数和正常 [(k-2)T月+δs[(k-3)Tf月+δs[(k-4)Tf月+ 数据小波系数的相似率的度量也只与其前一时刻的 δ5s[(k-5)Tf]-入,W[(k-1)Tf1- 状态相关,而与更早时刻的状态无关采用递归最小 A2W.[(k-2)Tf刀-入3W[(k-3)Tf月- 二乘法估计参数W和W): 入Ww[(k-4)Tf月-入5W,[(k-5)T,f月- W(kT)=σW.[(k-1)T]+(1-σ)W(kT), 入6W,w[(k-6)T,f月}. (2) W(kT)=g+(1-σ)[W(kT,f)-W(k-1)T]T· 式中:小波系数为因果序列.因此,可以利用前6个 [W,(kTf)-W(k -1)T]. 时刻的系数递归求取当前时刻的系数,实时性即得 已知观测序列和HMM模型参数,求得最优状 以保证 态序列是Viterbi算法所要解决的问题.文中预测跟 2基于HMM的UUV异常数据检测 踪过程中传感器所采集的信息为观测变量,只要对 观测序列中的数据进行优化即可实现孤立点的检 隐马尔可夫模型(HMM),即隐马尔可夫模型随 测,因此,利用Viterbi算法对原始数据所属状态(即 机动态系统,是双重随机过程:1)描述模型内部状 原始数据的属性为正常数据s1或为异常数据$。)进 态变化的基本随机过程,即马尔可夫过程q,;2)描 行实时判断.正常数据的分布较异常数据的规律性 述状态和观测值之间关系的随机过程 更强,更容易寻找规律,所以,通过考察正常数据的 马尔可夫过程由初始状态概率分布π=(π1, 分布情况,以正常数据分布作为基准,判断出异常数 T2,…,T)和状态转移矩阵A=(a)x来进行描 据的分布,即可检测出原始数据中的孤立点,并予以 述.其中,N表示模型的状态变量总数.令q,表示状 别除,以便得到干净的数据来进行UUV预测跟踪过 态过程,S={s1,s2,…,s}为隐藏状态集合,则初始 程中行为的自主决策。 状态概率元素描述为 定义1令E:=P:(We,W(kT,f月9,=s1) T;=P(q1=s:). (3)》 式(3)表示初始时刻过程状态为s:的概率.状态转 Hs≥0,1≤i≤N,aa=ITaI/∑‖T,‖,aw= 移矩阵元素描述为 I7/∑IT,,其中·1为集合的基数,T, a=P(9=s9-1=s:),1≤i,j≤N.(4) 式(4)表示t-1时刻状态为s,t时刻状态为s,的概 {ts(t)=js(t-l)=i},有p=∑(a(-e)-∑尚 率因为是标准随机约束,所以满足: (a1s:),则称p为异常值分布判定函数
式中: ψ ^ (w) 为 ψ(t) 的傅里叶转换,其 Z 变换为 ψ(z) = δ1 z -1 + δ2 z -2 + δ3 z -3 + δ4 z -4 + δ5 z -5 λ1 z -1 + λ2 z -2 + λ3 z -3 + λ4 z -4 + λ5 z -5 + λ6 z -6 . 式中: ε = e -fT(σ-iw0 ) , λ1 = - 6ε , λ2 = 15ε 2 , λ3 = - 20ε 3 , λ4 = 15ε 4 , λ5 = - 6ε 5 , λ6 = ε 6 , δ1 = (σfT) 3 / 3 - (σfT) 4 / 4 + (σfT) 5 [ / 5]·ε, δ2 = 10 (σfT) 3 - 25 (σfT) 4 + 26 (σfT) 5 [ ]·ε 2 / 15, δ3 = 66 (σfT) 5 - 30 (σfT) 3 [ ]·ε 3 / 15, δ4 = 10 (σfT) 3 + 25 (σfT) 4 + 26 (σfT) 5 [ ]·ε 4 / 15, δ5 = 10 (σfT) 3 + 5 (σfT) 4 + 2 (σfT) 5 [ ]·ε 5 / 30. 则小波系数的 Z 变换形式为 Ws(z) = T f [s(z)·ψ(z) ] . (1) 式中:s(z)为数据 s(t)的 Z 变换,T 表示周期,f 表示 频率.通过对式(1)进行 Z 反变换,可以得到小波系 数表示如下: Ws,ψ(kT,f) = fT {δ1 s [(k - 1)T,f] + δ2 s· [(k - 2)T,f] + δ3 s [(k - 3)T,f] + δ4 s [(k - 4)T,f] + δ5 s [(k - 5)T,f] - λ1Ws,ψ [(k - 1)T,f] - λ2Ws,ψ [(k - 2)T,f] - λ3Ws,ψ [(k - 3)T,f] - λ4Ws,ψ [(k - 4)T,f] - λ5Ws,ψ [(k - 5)T,f] - λ6Ws,ψ [(k - 6)T,f] }. (2) 式中:小波系数为因果序列. 因此,可以利用前 6 个 时刻的系数递归求取当前时刻的系数,实时性即得 以保证. 2 基于 HMM 的 UUV 异常数据检测 隐马尔可夫模型(HMM),即隐马尔可夫模型随 机动态系统,是双重随机过程:1) 描述模型内部状 态变化的基本随机过程,即马尔可夫过程 qt ;2)描 述状态和观测值之间关系的随机过程. 马尔可夫过程由初始状态概率分布 π = (π1 , π2 ,…,πN) 和状态转移矩阵 A = (aij) N×N 来进行描 述.其中,N 表示模型的状态变量总数.令 qt 表示状 态过程,S = {s1 ,s2 ,…,sN }为隐藏状态集合,则初始 状态概率元素描述为 πi = P(q1 = si). (3) 式(3)表示初始时刻过程状态为 si 的概率.状态转 移矩阵元素描述为 aij = P(qt = sj qt-1 = si),1 ≤ i,j ≤ N. (4) 式(4)表示 t-1 时刻状态为 si,t 时刻状态为 sj 的概 率.因为是标准随机约束,所以满足: aij ≥ 0, ∑ N j = 1 aij = 1. ì î í ï ï ïï 利用马尔可夫链表示预测跟踪过程中小波变换 重构后的数据异常情况.将小波转换后的小波系数 所表示的数据分为 2 种情况,即正常数据和异常数 据,其中 s1 表示正常数据, s0 表示异常数据.根据这 一划分标准,模型的状态变量总数 N = 2. 状态和观测值之间的随机过程用观测值概率矩 阵 B= (bki) N×N描述.bkt表示状态 qt 为 si 时第 k 时刻 小波系数 Ws( kT,f)与正常数据小波系数 Wm 的相 似率,观测概率矩阵元素和相似率分别为 bkt = P Wm ,Ws(kT,f) s = si [ ] , P [Wm,Ws(kT,f) s = k] = N Ws(kT,f) Wm,Wvar [ ] = exp - 1 2 Ws(kT,f) - Wm ( ) TW -1 var Ws(kT,f) - Wm ( ) é ë ê ê ù û ú ú . 式中:N[· ·] 为正态分布,Wvar为正常小波系数方差. 由于隐马尔可夫过程的实质是当前时刻的状态 只与其前一时刻的状态相关,因此,小波系数和正常 数据小波系数的相似率的度量也只与其前一时刻的 状态相关,而与更早时刻的状态无关.采用递归最小 二乘法估计参数 Wm 和 Wvar [5] : Wm(kT) = σWm [(k - 1)T] + (1 - σ)Ws(kT,f), Wvar(kT) = σ + (1 - σ) [Ws(kT,f) - Wvar(k - 1)T] T· [Ws(kT,f) - Wvar(k - 1)T] . 已知观测序列和 HMM 模型参数,求得最优状 态序列是 Viterbi 算法所要解决的问题.文中预测跟 踪过程中传感器所采集的信息为观测变量,只要对 观测序列中的数据进行优化即可实现孤立点的检 测,因此,利用 Viterbi 算法对原始数据所属状态(即 原始数据的属性为正常数据 s1 或为异常数据 s0 )进 行实时判断.正常数据的分布较异常数据的规律性 更强,更容易寻找规律,所以,通过考察正常数据的 分布情况,以正常数据分布作为基准,判断出异常数 据的分布,即可检测出原始数据中的孤立点,并予以 剔除,以便得到干净的数据来进行 UUV 预测跟踪过 程中行为的自主决策. 定义 1 令 εi = pi Wave , Ws(kT,f) qt = s1 ( ) , ∀ε ≥0,1 ≤ i ≤ N,ai1 = ‖Ti1‖/∑ N j = 1 ‖Tij‖,ai0 = ‖Ti0‖/∑ N j = 1 ‖Tij‖ ,其中‖·‖为集合的基数,Tij = {t:s(t)=j s(t-1)=i} ,有 φ= ∑ N i=1 ai0 1-εi ( ( ) ) - ∑ N i = 1 ai1εi ( ) ,则称 φ 为异常值分布判定函数. 第 6 期 穆岩,等:基于小波 HMM 的 UUV 传感器数据孤立点检测 ·553·

·554 智能系统学报 第8卷 判定条件:对于任意i,1≤i≤N,在状态s=s: 得的小波系数相比较,通过6个时刻的数据相互关 时,若p>0,则为正常数据,否则为异常数据 联,可以发现数据的变化规律.若剔除后数据的小波 根据定义1,对异常值分布情况进行实时更新, 系数与未剔除的小波系数无明显的波动,则待定孤 判定条件: 立点可以判定为孤立点:若小波系数变化明显,则可 (异常值,p>0: 判定其不为孤立点 正常值,p<0. 4 试验验证 根据判定条件对传感器采集的原始数据进行孤 立点检测,则可以得到精确的数据进行UUV预测跟 为了验证所提出算法的有效性,利用试验所得 踪的控制 数据进行孤立点的检测和分析.验证数据来自2010 年千岛湖试验.试验中UUV的外形尺寸为长5.0m, 3 惰性检测算法 直径p为0.8m. 所谓惰性算法(inertia algorithm),就是针对传 UUV的航向角由电罗经给出,速度由多普勒测 感器采集的数据利用小波HMM算法检测后得到的 速仪(DVL)给出,深度由深度计测得.在UUV的预测 孤立点进行延迟处理的方法,以此降低孤立点误判 跟踪过程中,水平面的跟踪主要通过控制速度和航向 的概率.本文中利用惰性算法重检测准孤立点(pre- 完成,而垂直面的跟踪则需要通过控制深度实现因 outlier),以提高检测结果的准确性。 此,分别对纵向速度、航向和深度进行孤立点检测并 定义2利用孤立点检测算法首次划定为孤立 予以处理,使所得的纵向速度、航向和深度的准确性 点的信息,定义为准孤立点. 提高,进而实现精确地预测跟踪文中参数f=50. 在式(5)中,当前时刻的小波系数依赖于其之 文中除了进行了孤立点检测及分析外,还进行 了残差分析残差与数据和模型相关,用于评价预测 前6个时刻的小波系数,因此,当前时刻的系数直接 影响着之后6个时刻的数据.由此考虑,检测到的孤 模型的精度.在文献[6-7]中,对残差的定义做出了 修正修正的残差定义为 立点会影响到之后的小波系数,其检测的正确与否 会直接影响UUV预测跟踪中的自主决策.若检测结 d4s=Z/V√Y4 果错误,则预测跟踪可能会偏离正确的航迹.待定孤 式中:Z.马为标准化的残差,其定义为 立点的妥善处理对于UUV预测跟踪是进一层保证. Zg=(C.鸟-eA.马)/√e,g 由于本文所提出的算法立足于UUV的实践活动,所 式中:C,鸟为A和B同时发生次数.Y为Z马 以必须全面考虑安全性和实用性,尽可能提高算法 的方差的最大似然估计,其定义为 的精确性和实时性. 为了避免这种误判的发生,本文引入了备选集 M R来暂时存放首次检测为孤立点的数据,并将这些 孤立点称作待定孤立点O。.令待定孤立点的小波系 式中:M=∑∑C,m,和m为A和B的 数表示为W。.,对于Ho.∈R,3k≥6,使得 个数.e.为同时发生A,和B,的期望,定义为 W,(kT,)由其之前6个时刻的系数和其之前5个 ∑cs∑Cg 时刻的数据同时决定. eA.B M 由于孤立点的数量相对于正常数据来说属于离 4.1速度验证 散数据,数量较少,因此,对其进行再检验不会影响 利用UUV预测跟踪过程中的纵向速度原始数 实时性假设k。时刻的数据被检测为孤立点,则其会 据验证文中提出的孤立点检测方法.将原始数据进 对k。+1~k。+6的小波系数都造成影响,若该点检 行小波变换,并根据所得的变换结果,判定孤立点的 测结果错误,会导致之后的系数产生误差,甚至造成 分布.检测结果如图2所示. 误差的发散,所得的结果可能为错误值,从而导致 1.74 UUV错误地预测.为了说明惰性算法对待定孤立点 1.72 www 的重检测,具体方法阐述如下: 1)将k。时刻的待定孤立点O放入备选集R; 1.680 50100150200250300 t/s 2)将0.作为k。时刻的系数带入到式(5)中,预 (a)原始速度 测k。+1~k。+6的小波系数,将其与剔除O.后所
判定条件:对于任意 i, 1 ≤ i ≤ N ,在状态 s = si 时,若 φ > 0,则为正常数据,否则为异常数据. 根据定义 1,对异常值分布情况进行实时更新, 判定条件: 异常值,φ > 0; 正常值,φ < 0. { 根据判定条件对传感器采集的原始数据进行孤 立点检测,则可以得到精确的数据进行 UUV 预测跟 踪的控制. 3 惰性检测算法 所谓惰性算法( inertia algorithm),就是针对传 感器采集的数据利用小波 HMM 算法检测后得到的 孤立点进行延迟处理的方法,以此降低孤立点误判 的概率.本文中利用惰性算法重检测准孤立点( pre⁃ outlier),以提高检测结果的准确性. 定义 2 利用孤立点检测算法首次划定为孤立 点的信息,定义为准孤立点. 在式(5)中,当前时刻的小波系数依赖于其之 前 6 个时刻的小波系数,因此,当前时刻的系数直接 影响着之后 6 个时刻的数据.由此考虑,检测到的孤 立点会影响到之后的小波系数,其检测的正确与否 会直接影响 UUV 预测跟踪中的自主决策.若检测结 果错误,则预测跟踪可能会偏离正确的航迹.待定孤 立点的妥善处理对于 UUV 预测跟踪是进一层保证. 由于本文所提出的算法立足于 UUV 的实践活动,所 以必须全面考虑安全性和实用性,尽可能提高算法 的精确性和实时性. 为了避免这种误判的发生,本文引入了备选集 R 来暂时存放首次检测为孤立点的数据,并将这些 孤立点称作待定孤立点 Ow .令待定孤立点的小波系 数表 示 为 Wow , 对 于 ∀ow ∈ R , ∃k ≥ 6, 使 得 Ws,ψ(kT,f) 由其之前 6 个时刻的系数和其之前 5 个 时刻的数据同时决定. 由于孤立点的数量相对于正常数据来说属于离 散数据,数量较少,因此,对其进行再检验不会影响 实时性.假设 k0 时刻的数据被检测为孤立点,则其会 对 k0 + 1 ~ k0 + 6 的小波系数都造成影响,若该点检 测结果错误,会导致之后的系数产生误差,甚至造成 误差的发散,所得的结果可能为错误值,从而导致 UUV 错误地预测.为了说明惰性算法对待定孤立点 的重检测,具体方法阐述如下: 1)将 k0 时刻的待定孤立点 Ow 放入备选集 R ; 2)将 Ow 作为 k0 时刻的系数带入到式(5)中,预 测 k0 + 1~ k0 + 6 的小波系数,将其与剔除 Ow 后所 得的小波系数相比较,通过 6 个时刻的数据相互关 联,可以发现数据的变化规律.若剔除后数据的小波 系数与未剔除的小波系数无明显的波动,则待定孤 立点可以判定为孤立点;若小波系数变化明显,则可 判定其不为孤立点. 4 试验验证 为了验证所提出算法的有效性,利用试验所得 数据进行孤立点的检测和分析.验证数据来自 2010 年千岛湖试验.试验中 UUV 的外形尺寸为长 5.0 m, 直径 φ 为 0.8 m. UUV 的航向角由电罗经给出,速度由多普勒测 速仪(DVL)给出,深度由深度计测得.在 UUV 的预测 跟踪过程中,水平面的跟踪主要通过控制速度和航向 完成,而垂直面的跟踪则需要通过控制深度实现.因 此,分别对纵向速度、航向和深度进行孤立点检测并 予以处理,使所得的纵向速度、航向和深度的准确性 提高,进而实现精确地预测跟踪.文中参数 f = 50. 文中除了进行了孤立点检测及分析外,还进行 了残差分析.残差与数据和模型相关,用于评价预测 模型的精度.在文献[6⁃7]中,对残差的定义做出了 修正.修正的残差定义为 dAi ,Bj = ZAi ,Bj / γAi ,Bj . 式中: ZAi ,Bj 为标准化的残差,其定义为 ZAi ,Bj = CAi ,Bj - eAi ,Bj ( ) / eAi ,Bj . 式中: CAi ,Bj 为 Ai 和 Bj 同时发生次数. γ Ai ,Bj 为 ZAi ,Bj 的方差的最大似然估计,其定义为 γAi ,Bj = 1 - ∑ mA i = 1 CAi ,Bj M æ è ç ç ö ø ÷ ÷ 1 - ∑ mB j = 1 CAi ,Bj M æ è ç ç ö ø ÷ ÷ . 式中: M = ∑ mA i = 1∑ mB j = 1 CAi ,Bj , mA 和 mB 为 A 和 B 的 个数. eAi ,Bj 为同时发生 Ai 和 Bj 的期望,定义为 eAi ,Bj = ∑ mA i = 1 CAi ,Bj∑ mB j = 1 CAi ,Bj M . 4.1 速度验证 利用 UUV 预测跟踪过程中的纵向速度原始数 据验证文中提出的孤立点检测方法.将原始数据进 行小波变换,并根据所得的变换结果,判定孤立点的 分布.检测结果如图 2 所示. (a)原始速度 ·554· 智 能 系 统 学 报 第 8 卷
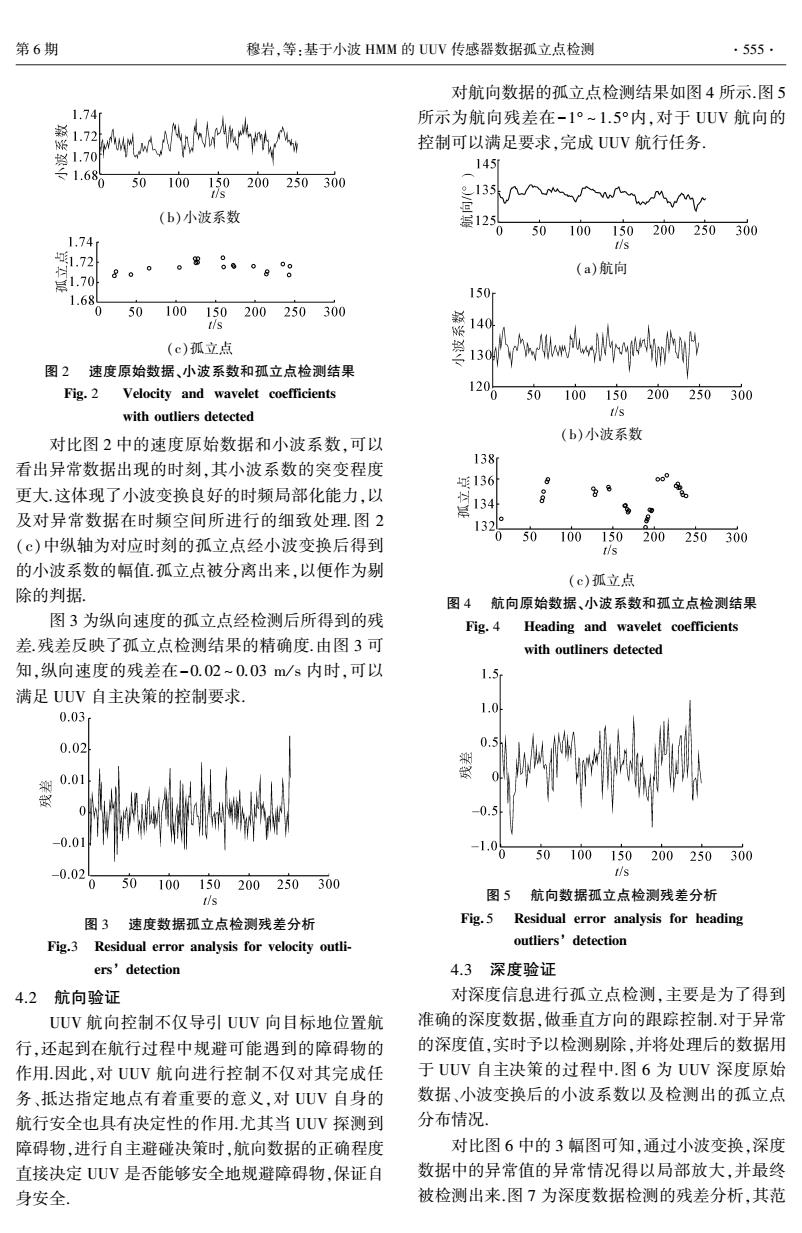
第6期 穆岩,等:基于小波HMM的UUV传感器数据孤立点检测 ·555. 对航向数据的孤立点检测结果如图4所示.图5 1.74 所示为航向残差在-1°~1.5内,对于UUV航向的 1.72 N 控制可以满足要求,完成UUV航行任务。 145 50 100 150 200250300 (b)小波系数 福12 0 50100150200250300 1.74 tis 8、。g8 (a)航向 1.68 150 0 50100 150200250300 d 140 (c)孤立点 人we4pr 图2速度原始数据、小波系数和孤立点检测结果 Fig.2 Velocity and wavelet coefficients 1206 50 100150200250300 with outliers detected tis 对比图2中的速度原始数据和小波系数,可以 (b)小波系数 138 看出异常数据出现的时刻,其小波系数的突变程度 136 8 更大这体现了小波变换良好的时频局部化能力,以 8 88 134 及对异常数据在时频空间所进行的细致处理图2 132 0 (c)中纵轴为对应时刻的孤立点经小波变换后得到 50 100150200250300 t/s 的小波系数的幅值孤立点被分离出来,以便作为剔 (c)孤立点 除的判据. 图4航向原始数据、小波系数和孤立点检测结果 图3为纵向速度的孤立点经检测后所得到的残 Fig.4 Heading and wavelet coefficients 差.残差反映了孤立点检测结果的精确度.由图3可 with outliners detected 知,纵向速度的残差在-0.02~0.03m/s内时,可以 1.5 满足UUV自主决策的控制要求. 0.03 1.0 0.02 0.01 -0.01 50100150200250300 -0.02 tis 0 50100150200250.300 tis 图5航向数据孤立点检测残差分析 图3速度数据孤立点检测残差分析 Fig.5 Residual error analysis for heading Fig.3 Residual error analysis for velocity outli- outliers'detection ers'detection 4.3深度验证 4.2航向验证 对深度信息进行孤立点检测,主要是为了得到 UUV航向控制不仅导引UUV向目标地位置航 准确的深度数据,做垂直方向的跟踪控制对于异常 行,还起到在航行过程中规避可能遇到的障碍物的 的深度值,实时予以检测剔除,并将处理后的数据用 作用因此,对UUV航向进行控制不仅对其完成任 于UUV自主决策的过程中.图6为UUV深度原始 务、抵达指定地点有着重要的意义,对UUV自身的 数据、小波变换后的小波系数以及检测出的孤立点 航行安全也具有决定性的作用.尤其当UUV探测到 分布情况. 障碍物,进行自主避碰决策时,航向数据的正确程度 对比图6中的3幅图可知,通过小波变换,深度 直接决定UUV是否能够安全地规避障碍物,保证自 数据中的异常值的异常情况得以局部放大,并最终 身安全 被检测出来图7为深度数据检测的残差分析,其范
(b)小波系数 (c)孤立点 图 2 速度原始数据、小波系数和孤立点检测结果 Fig. 2 Velocity and wavelet coefficients with outliers detected 对比图 2 中的速度原始数据和小波系数,可以 看出异常数据出现的时刻,其小波系数的突变程度 更大.这体现了小波变换良好的时频局部化能力,以 及对异常数据在时频空间所进行的细致处理.图 2 (c)中纵轴为对应时刻的孤立点经小波变换后得到 的小波系数的幅值.孤立点被分离出来,以便作为剔 除的判据. 图 3 为纵向速度的孤立点经检测后所得到的残 差.残差反映了孤立点检测结果的精确度.由图 3 可 知,纵向速度的残差在-0.02 ~ 0.03 m / s 内时,可以 满足 UUV 自主决策的控制要求. 图 3 速度数据孤立点检测残差分析 Fig.3 Residual error analysis for velocity outli⁃ ers’ detection 4.2 航向验证 UUV 航向控制不仅导引 UUV 向目标地位置航 行,还起到在航行过程中规避可能遇到的障碍物的 作用.因此,对 UUV 航向进行控制不仅对其完成任 务、抵达指定地点有着重要的意义,对 UUV 自身的 航行安全也具有决定性的作用.尤其当 UUV 探测到 障碍物,进行自主避碰决策时,航向数据的正确程度 直接决定 UUV 是否能够安全地规避障碍物,保证自 身安全. 对航向数据的孤立点检测结果如图 4 所示.图 5 所示为航向残差在-1° ~ 1.5°内,对于 UUV 航向的 控制可以满足要求,完成 UUV 航行任务. (a)航向 (b)小波系数 (c)孤立点 图 4 航向原始数据、小波系数和孤立点检测结果 Fig. 4 Heading and wavelet coefficients with outliners detected 图 5 航向数据孤立点检测残差分析 Fig. 5 Residual error analysis for heading outliers’ detection 4.3 深度验证 对深度信息进行孤立点检测,主要是为了得到 准确的深度数据,做垂直方向的跟踪控制.对于异常 的深度值,实时予以检测剔除,并将处理后的数据用 于 UUV 自主决策的过程中.图 6 为 UUV 深度原始 数据、小波变换后的小波系数以及检测出的孤立点 分布情况. 对比图 6 中的 3 幅图可知,通过小波变换,深度 数据中的异常值的异常情况得以局部放大,并最终 被检测出来.图 7 为深度数据检测的残差分析,其范 第 6 期 穆岩,等:基于小波 HMM 的 UUV 传感器数据孤立点检测 ·555·

·556· 智能系统学报 第8卷 围在-0.1~0.2m. 测的准确性由残差分析可知,所得到的孤立点检测 2 结果可以满足各自的精度要求范围.处理后的数据 可以用于UUV的预测跟踪,并能够保证数据的准确 性.4)湖试数据验证了文中提出算法的有效性和实 50100150200250300 用性 (a)深度 参考文献: 2 [1]CHAARI O,MEUNIER M,BROUAYE F.Wavelets:a new tool for the resonant grounded power distribution systems re- laying[J].IEEE Transactions on Power Delivery,1996,11 50 100150200250300 (3):1301-1308. 1/s [2]侯传宇.马尔可夫及隐马尔可夫模型在数据挖掘中的应 (b)小波系数 用J].电脑知识与技术,2008,1(7):1186-1189. 4 HOU Chuanyu.The application of Markov models and hid- 8 8 den Markov models in data mining[J.Computer Knowledge 0 0 。0 0 and Technolog,2008,1(7):1186-1189. 0 [3]朱嘉瑜,高鹰.基于改进粒子群算法的隐马尔可夫模型 40 50100150200250300 训练[J].计算机工程与设计,2010,31(1):157-160. ts (c)孤立点 ZHU Jiayu,GAO Ying.Adaptive particle swarm optimiza- 图6深度原始数据、小波系数和孤立点检测结果 tion for hidden Markov model training[J].Computer Engi- Fig.6 Depth and its wavelet coefficients neering and Design,2010,31(1):157-160. with outliners detected [4]敬晓龙.小波变换在隐马尔可夫模型非参数估计中的应 用[D].成都:四川大学,2003:2-9. 0.2 JING Xiaolong.Wavelet transformation for nonparametric es- 0.1 timation of HMM's[D].Chengdu:Sichuan University, 2003:2-9. [5]刘芳,毛志忠.基于小波马尔可夫模型的控制过程异常 数据检测方法[J].控制与决策,2011,26(8):1187- 1191 LIU Fang,MAO Zhizhong.Outlier detection for control 50100150200250300 process data based on wavelet-HMM methods []]Control t/s and Decision,2011,26(8):1187-1191. 图7深度数据孤立点检测残差分析 [6]CHAN K CC,WONG A K C.APACS:a system for the au- Fig.7 Residual error analysis for depth outliers' tomatic analysis and classification of conceptual patterns detection [J].Computational Intelligence,1990.6(3):119-131. 5 结束语 [7]CHAN K CC,WONG A K C.Statistical technique for ex- tracting classificatory knowledge from databases[M].[S. 本文针对UUV预测跟踪过程中传感器测得数 1.]:AAA/MIT Press,1991:107-124. 据的不准确问题,提出了利用小波HMM检测异常 [8]董红斌,贺志.协同演化算法及其在数据挖掘中的应用 数据的算法.1)利用改进递归小波转换将传感器采 [M].北京:中国水利水电出版社,2008:86-89. 集的原始数据用小波系数进行表示,使得数据中的 [9]STRUZIK Z R,SIEBES A P J M.Wavelet transform based 孤立点得到局部放大.利用历史小波系数进行递归 multifractal formalism in outlier detection and localisation for financial time series[J].Physica A,2002,309(3):388- 更新,实时性可以得以保证.2)结合隐马尔可夫模 402 型,引入判定定理,分析转换后的小波系数,若某时 [10]JUANG B H,RABINER L R.The segmental k-means al- 刻小波系数明显异于其他时刻的小波系数,则判定 gorithm for estimating the parameters of hidden Markov 其为孤立点,进而对异常数据进行检测、剔除.3)准 models[J].IEEE Transactions on Acoustics,Speech,Sig- 孤立点通过惰性算法进行重检测,以提高孤立点检 nal Processing,.1990,38(9):1639-1641
围在-0.1~0.2 m. (a)深度 (b)小波系数 (c)孤立点 图 6 深度原始数据、小波系数和孤立点检测结果 Fig. 6 Depth and its wavelet coefficients with outliners detected 图 7 深度数据孤立点检测残差分析 Fig.7 Residual error analysis for depth outliers’ detection 5 结束语 本文针对 UUV 预测跟踪过程中传感器测得数 据的不准确问题,提出了利用小波 HMM 检测异常 数据的算法.1)利用改进递归小波转换将传感器采 集的原始数据用小波系数进行表示,使得数据中的 孤立点得到局部放大.利用历史小波系数进行递归 更新,实时性可以得以保证.2) 结合隐马尔可夫模 型,引入判定定理,分析转换后的小波系数,若某时 刻小波系数明显异于其他时刻的小波系数,则判定 其为孤立点,进而对异常数据进行检测、剔除.3)准 孤立点通过惰性算法进行重检测,以提高孤立点检 测的准确性.由残差分析可知,所得到的孤立点检测 结果可以满足各自的精度要求范围.处理后的数据 可以用于 UUV 的预测跟踪,并能够保证数据的准确 性.4)湖试数据验证了文中提出算法的有效性和实 用性. 参考文献: [1]CHAARI O, MEUNIER M, BROUAYE F. Wavelets: a new tool for the resonant grounded power distribution systems re⁃ laying[J]. IEEE Transactions on Power Delivery, 1996, 11 (3): 1301⁃1308. [2]侯传宇. 马尔可夫及隐马尔可夫模型在数据挖掘中的应 用[J]. 电脑知识与技术, 2008, 1(7): 1186⁃1189. HOU Chuanyu. The application of Markov models and hid⁃ den Markov models in data mining[J]. Computer Knowledge and Technology, 2008, 1(7): 1186⁃1189. [3]朱嘉瑜, 高鹰. 基于改进粒子群算法的隐马尔可夫模型 训练[J]. 计算机工程与设计, 2010, 31(1): 157⁃160. ZHU Jiayu, GAO Ying. Adaptive particle swarm optimiza⁃ tion for hidden Markov model training[ J]. Computer Engi⁃ neering and Design, 2010, 31(1): 157⁃160. [4]敬晓龙. 小波变换在隐马尔可夫模型非参数估计中的应 用[D]. 成都: 四川大学, 2003: 2⁃9. JING Xiaolong. Wavelet transformation for nonparametric es⁃ timation of HMM’ s [ D]. Chengdu: Sichuan University, 2003: 2⁃9. [5]刘芳,毛志忠. 基于小波马尔可夫模型的控制过程异常 数据检测方法[ J]. 控制与决策, 2011,26 ( 8): 1187⁃ 1191. LIU Fang, MAO Zhizhong. Outlier detection for control process data based on wavelet⁃HMM methods [ J]. Control and Decision, 2011, 26(8): 1187⁃1191. [6]CHAN K C C, WONG A K C. APACS: a system for the au⁃ tomatic analysis and classification of conceptual patterns [J]. Computational Intelligence, 1990, 6(3): 119⁃131. [7]CHAN K C C, WONG A K C. Statistical technique for ex⁃ tracting classificatory knowledge from databases [ M]. [ S. l.]: AAAI/ MIT Press, 1991: 107⁃124. [8]董红斌,贺志. 协同演化算法及其在数据挖掘中的应用 [M]. 北京:中国水利水电出版社, 2008: 86⁃89. [9]STRUZIK Z R, SIEBES A P J M. Wavelet transform based multifractal formalism in outlier detection and localisation for financial time series[J]. Physica A, 2002, 309(3): 388⁃ 402. [10]JUANG B H, RABINER L R. The segmental k⁃means al⁃ gorithm for estimating the parameters of hidden Markov models[J]. IEEE Transactions on Acoustics, Speech, Sig⁃ nal Processing, 1990, 38(9): 1639⁃1641. ·556· 智 能 系 统 学 报 第 8 卷

第6期 穆岩,等:基于小波HMM的UUV传感器数据孤立点检测 ·557. [11]ZHANG Chuanli,HUANG Yizhuang,MA Xiaoxu,et al. 侯恕葬,女,1972年生,副教授,主 A new approach to detect transformer inrush current by ap- 要研究方向为水下特种作业技术与装 plying wavelet transform[C]//1998 International Confer- 备主持国家自然科学基金、黑龙江省 ence on Power System Technology.Beijing,China,1998: 自然科学基金、哈尔滨市科技创新人才 1040-1044. 专项资金及海工横向项目4项,参与国 作者简介: 4防预研、国家“863”专项及横向课题4 穆岩,男,1980年生,工程师,主要 项.发表学术论文20余篇,获省部级科学技术奖励2次. 研究方向为船舶机电设备和水下无人 迟冬南,女,1985年生,博士,主要 航行器技术研究,发表学术论文6篇. 研究方向为水下无人航行器运动控制 技术,发表学术论文9篇 2014年智慧城市和城市基础设施工程进展国际会议 2014 International Conference on Wisdom City and Advances in City Infrastructure Engineering WCCIE 2014) 2014 International Conference on Wisdom City and Advances in City Infrastructure Engineering WCCIE 2014)will be held in Zhangjiajie on January 10-11,2014. The idea of WCCIE 2014 is for the scientists,scholars,engineers and students from the universities all around the world and the industry to present ongoing research activities,and hence to foster research relations between the universities and the industry.This conference provides opportunities for the delegates to exchange and share their experiences,present research results,explore collaborations and to spark new ideas,with the aim of developing new projects and exploiting new technology in this field. Topics including but not limited to: 1)Intelligent computing and applications 2)Wisdom city 3)City infrastructure engineering 4)Urban intelligent building and green building 5)City intelligence transportation and logistics 6)Automation of city construction All full paper submissions will be peer reviewed and evaluated based on originality,technical and/or research con- tent/depth,correctness,relevance to conference,contributions,and readability. All the accepted papers will be published by CPS and arranged EI index and Selected excellent papers of the proc- ceedings (about 20%)will be published in the EI Source and SCI Source Journals,which are listed as follows: 1)Automation in Construction ISSN:0926-5805,Impact factor 1.702) 2)Applied Clay Science (ISSN:0169-1317,Impact factor:3.060) 3)Journal of Software(ISSN:1796-217X) 4)Journal of Networks(ISSN:1796-2056) 5)Journal of Computers(ISSN:1796-203X) 6)Environmental Engineering Research(ISSN:1226-1025) Send the paper(s)to wccie2014 @163.com
[11] ZHANG Chuanli, HUANG Yizhuang, MA Xiaoxu, et al. A new approach to detect transformer inrush current by ap⁃ plying wavelet transform[C] / / 1998 International Confer⁃ ence on Power System Technology. Beijing, China, 1998: 1040⁃1044. 作者简介: 穆岩,男,1980 年生,工程师,主要 研究方向为船舶机电设备和水下无人 航行器技术研究,发表学术论文 6 篇. 侯恕萍,女,1972 年生,副教授,主 要研究方向为水下特种作业技术与装 备.主持国家自然科学基金、黑龙江省 自然科学基金、哈尔滨市科技创新人才 专项资金及海工横向项目 4 项,参与国 防预研、国家“ 863” 专项及横向课题 4 项.发表学术论文 20 余篇,获省部级科学技术奖励 2 次. 迟冬南,女,1985 年生,博士,主要 研究方向为水下无人航行器运动控制 技术,发表学术论文 9 篇. 2014 年智慧城市和城市基础设施工程进展国际会议 2014 International Conference on Wisdom City and Advances in City Infrastructure Engineering (WCCIE 2014) 2014 International Conference on Wisdom City and Advances in City Infrastructure Engineering (WCCIE 2014) will be held in Zhangjiajie on January 10-11,2014. The idea of WCCIE 2014 is for the scientists, scholars, engineers and students from the universities all around the world and the industry to present ongoing research activities, and hence to foster research relations between the universities and the industry. This conference provides opportunities for the delegates to exchange and share their experiences, present research results, explore collaborations and to spark new ideas, with the aim of developing new projects and exploiting new technology in this field. Topics including but not limited to: 1) Intelligent computing and applications 2) Wisdom city 3) City infrastructure engineering 4) Urban intelligent building and green building 5) City intelligence transportation and logistics 6) Automation of city construction All full paper submissions will be peer reviewed and evaluated based on originality, technical and / or research con⁃ tent / depth, correctness, relevance to conference, contributions, and readability. All the accepted papers will be published by CPS and arranged EI index and Selected excellent papers of the proc⁃ ceedings (about 20%) will be published in the EI Source and SCI Source Journals,which are listed as follows: 1) Automation in Construction ( ISSN: 0926-5805,Impact factor 1.702 ) 2) Applied Clay Science (ISSN: 0169-1317,Impact factor:3.060) 3) Journal of Software( ISSN:1796⁃217X) 4) Journal of Networks(ISSN:1796⁃2056) 5) Journal of Computers(ISSN:1796⁃203X) 6) Environmental Engineering Research(ISSN:1226⁃1025) Send the paper(s) to wccie2014 @ 163.com 第 6 期 穆岩,等:基于小波 HMM 的 UUV 传感器数据孤立点检测 ·557·