
第8卷第6期 智能系统学报 Vol.8 No.6 2013年12月 CAAI Transactions on Intelligent Systems Dec.2013 D0:10.3969/j.issn.1673-4785.201306032 网络出版地址:htp:/www.cmki.net/kcms/detail/23.1538.TP.20131012.1815.008.html 基于切换模糊化的滑模变结构AUV姿态控制 郝阳12,赵新华2 (1.中国人民解放军91439部队,辽宁大连116041:2.哈尔滨工程大学自动化学院,黑龙江哈尔滨150001) 摘要:针对自主水下航行器(AUV)控制的要求,为解决姿态控制问题,提出了一种基于切换模糊化的滑模变结构 控制方法该方法结合了模糊控制与滑模变结构的优点,其中模糊控制以变结构控制的切换函数为输入,变结构控制 切换项为输出,在此基础上采用指数趋近律方法设计滑模变结构控制器.分别对该方法与传统滑模变结构控制方法 进行对比仿真,结果表明,该控制方法可以有效抑制滑模变结构控制的抖振现象,对模型不确定系统具有较强的鲁 棒性和一定的抗干扰能力. 关键词:模糊控制;滑模变结构控制;自主水下航行器;姿态控制;切换模糊化 中图分类号:TP273文献标志码:A文章编号:1673-4785(2013)06-0532-05 中文引用格式:郝阳,赵新华.基于切换模糊化的滑模变结构AUV姿态控制[J].智能系统学报,2013,8(6):532-536 英文引用格式:HAO Yang,ZHAO Xinhua.Slide-mode variable-structure AUV attitude control on the basis of fuz四y switching[J]. CAAI Transactions on Intelligent Systems,2013,8(6):532-536. Slide-mode variable-structure AUV attitude control on the basis of fuzzy switching HAO Yang'.2,ZHAO Xinhua? (1.Unit 91439 of PLA,Dalian 116041,China;2.College of Automation,Harbin Engineering University,Harbin 150001,China) Abstract:According to the control requirements of the autonomous underwater vehicle (AUV),and in order to solve the attitude control problem,a slide-mode variable-structure control method based on fuzzy switching is pro- posed.This method combines the merits of fuzzy control and slide-mode variable-structure,in which the fuzzy con- trol takes the switching function of the variable-structure control as the input,and the switching item of the variable- structure control as the output.On the basis of this,the exponential reaching law method is applied to the design of the slide-mode variable-structure controller.By comparison and simulation of the method and the traditional slide- mode variable-structure control method,the results show that the method may effectively suppress the chattering phenomenon of the slide-mode variable-structure control,and has strong robustness and anti-jamming capability for the model uncertainty system. Keywords:fuzzy control;slide-mode variable-structure control;autonomous underwater vehicle;attitude control; fuzzy switching AUV(autonomous underwater vehicle)控制系统 在削弱滑模变结构控制抖振现象的同时保持其对模 设计需要克服的困难主要有:被控对象模型和水动 型要求低、参数变化及扰动不灵敏等优点,适合用来 力参数的不确定性以及海浪和海流等随机扰动的影 解决AUV控制问题.这方面,研究人员已经开展了 响,这就要求其控制系统具有较强的鲁棒性和抗干 卓有成效的工作:施小成等山为AUV纵摇运动设计 扰能力.模糊控制与滑模控制的组合控制策略可以 了一种模糊滑模控制器:魏英杰等[☒]分别提出了一 种AUV模糊变结构控制方法和一种自适应模糊变 收稿日期:2013-06-21.网络出版日期:2013-10-12 结构控制方法[):沈建森等4为远程AUV近水面 基金项目:国家自然科学基金资助项目(50909027). 通信作者:赵新华.E-mail:xh huahua@163.com 运动提出了一种纵向模糊滑模控制方法:阚如文[)
第 8 卷第 6 期 智 能 系 统 学 报 Vol.8 №.6 2013 年 12 月 CAAI Transactions on Intelligent Systems Dec. 2013 DOI:10.3969 / j.issn.1673⁃4785.201306032 网络出版地址:http: / / www.cnki.net / kcms/ detail / 23.1538.TP.20131012.1815.008.html 基于切换模糊化的滑模变结构 AUV 姿态控制 郝阳1,2 ,赵新华2 (1.中国人民解放军 91439 部队,辽宁 大连 116041; 2. 哈尔滨工程大学 自动化学院,黑龙江 哈尔滨 150001) 摘 要:针对自主水下航行器(AUV)控制的要求,为解决姿态控制问题,提出了一种基于切换模糊化的滑模变结构 控制方法.该方法结合了模糊控制与滑模变结构的优点,其中模糊控制以变结构控制的切换函数为输入,变结构控制 切换项为输出,在此基础上采用指数趋近律方法设计滑模变结构控制器. 分别对该方法与传统滑模变结构控制方法 进行对比仿真,结果表明,该控制方法可以有效抑制滑模变结构控制的抖振现象,对模型不确定系统具有较强的鲁 棒性和一定的抗干扰能力. 关键词:模糊控制;滑模变结构控制;自主水下航行器;姿态控制;切换模糊化 中图分类号: TP273 文献标志码:A 文章编号:1673⁃4785(2013)06⁃0532⁃05 中文引用格式:郝阳,赵新华. 基于切换模糊化的滑模变结构 AUV 姿态控制[J]. 智能系统学报, 2013, 8(6): 532⁃536. 英文引用格式:HAO Yang, ZHAO Xinhua. Slide⁃mode variable⁃structure AUV attitude control on the basis of fuzzy switching[J]. CAAI Transactions on Intelligent Systems, 2013, 8(6): 532⁃536. Slide⁃mode variable⁃structure AUV attitude control on the basis of fuzzy switching HAO Yang 1,2 , ZHAO Xinhua 2 (1.Unit 91439 of PLA, Dalian 116041, China; 2.College of Automation, Harbin Engineering University, Harbin 150001, China) Abstract:According to the control requirements of the autonomous underwater vehicle (AUV),and in order to solve the attitude control problem, a slide⁃mode variable⁃structure control method based on fuzzy switching is pro⁃ posed. This method combines the merits of fuzzy control and slide⁃mode variable⁃structure, in which the fuzzy con⁃ trol takes the switching function of the variable⁃structure control as the input, and the switching item of the variable⁃ structure control as the output. On the basis of this, the exponential reaching law method is applied to the design of the slide⁃mode variable⁃structure controller. By comparison and simulation of the method and the traditional slide⁃ mode variable⁃structure control method, the results show that the method may effectively suppress the chattering phenomenon of the slide⁃mode variable⁃structure control, and has strong robustness and anti⁃jamming capability for the model uncertainty system. Keywords:fuzzy control; slide⁃mode variable⁃structure control; autonomous underwater vehicle; attitude control; fuzzy switching 收稿日期:2013⁃06⁃21. 网络出版日期:2013⁃10⁃12. 基金项目:国家自然科学基金资助项目(50909027). 通信作者:赵新华. E⁃mail:zxh_huahua@ 163.com. AUV( autonomous underwater vehicle) 控制系统 设计需要克服的困难主要有:被控对象模型和水动 力参数的不确定性以及海浪和海流等随机扰动的影 响,这就要求其控制系统具有较强的鲁棒性和抗干 扰能力.模糊控制与滑模控制的组合控制策略可以 在削弱滑模变结构控制抖振现象的同时保持其对模 型要求低、参数变化及扰动不灵敏等优点,适合用来 解决 AUV 控制问题. 这方面,研究人员已经开展了 卓有成效的工作:施小成等[1]为 AUV 纵摇运动设计 了一种模糊滑模控制器;魏英杰等[2] 分别提出了一 种 AUV 模糊变结构控制方法和一种自适应模糊变 结构控制方法[3] ;沈建森等[4] 为远程 AUV 近水面 运动提出了一种纵向模糊滑模控制方法;阚如文[5]

第6期 郝阳,等:基于切换模糊化的滑模变结构AUV姿态控制 ·533. 为无人水下航行器设计了一种改进型模糊滑模控制 P1=0.7p, 器和一种自适应模糊滑模控制器.本文采用模糊控 P2=1.3p. 制的输出代替符号函数作为滑模变结构控制的切换 实际水动力系数将在P1和P2之间变化,进而可 项来柔化控制信号,反复调整隶属函数以获得更好 以得到系统状态方程的下限形式和上限形式. 的控制效果,有效克服了模型参数不确定和海洋随 基于水动力系数P,的系统状态方程为[四 机扰动的影响,通过仿真对比验证了该方法的控制 「-0.950 1.150 -0.021 01 性能、鲁棒性、抗干扰能力和抑制抖振的能力」 9.280 -0.615 0.858 0 1AUV数学模型及其线性化 0 1.000 0 0 1.000 0 -2.000 0 为了便于控制系统的分析与设计,通常将AUV 六自由度运动分解为垂直面运动和水平面运动,本 -0.063 文只研究AUV在垂直面内的姿态控制.由于AUV -0.615 6 (2) 姿态控制可以看作受到扰动作用后在平衡位置附近 0 做小幅度运动,因此基于小扰动法对其垂直面模型 0 做线性化处理6,得到☒: 基于水动力系数P,的系统状态方程为 m -Z Za 001「w 「-1.190 0.730 -0.020 0 -M: 1n-M00 q 6.680-0.718 0.603 0 0 0 0 a 0 1.000 0 0 0 0 0 1.000 0 -2.0000」z」 Zu (Z+m)u 0 0 -0.078 Mu Mu 0 0 -0.796 0 0 (3) 0 1 0 u 0 0 0 式中:m为AUV质量;I为转动惯量;Z和M为水动 力系数[6;z、0分别为深度和纵摇角:u、0和g分 2控制方法 别为纵荡速度、升沉速度和纵摇角速度:8为水平舵 基于切换模糊化的滑模变结构AUV姿态控制 角.取轴向速度为2m/s,基于某典型AUV水动力系 方法的原理框图如图1所示. 数建立系统标称状态方程为 切换 模糊 趋近律 变结构 控制 控制 航行器 0 -1.040 0.865 -0.020 0][w Z/0 传感器 6.000 -0.681 0.708 0 9 + 图1控制方法原理框图 0 1.000 0 0 Fig.1 Block diagram of the control method 1.000 0 -2.000 oL=] 图1中,Z,、6。为期望深度和纵摇角,即平衡状 -0.072 态,Z、日为实际深度和纵摇角:δ为水平舵角, -0.722 (1) 2.1滑模变结构控制 0 针对如下线性系统: 0 (住=Ax+B(u+ft)), 考虑到模型的不确定性,设所有相关水动力系 (4) s =Cx. 数有30%的相对不确定度),P为水动力系数标称 式中:A和B取自式(1),容易验证(A,B)完全能 值,P1和P2分别为水动力系数下限值和上限值: 控,因此系统可以任意配置极点[),本文采用
为无人水下航行器设计了一种改进型模糊滑模控制 器和一种自适应模糊滑模控制器.本文采用模糊控 制的输出代替符号函数作为滑模变结构控制的切换 项来柔化控制信号,反复调整隶属函数以获得更好 的控制效果,有效克服了模型参数不确定和海洋随 机扰动的影响,通过仿真对比验证了该方法的控制 性能、鲁棒性、抗干扰能力和抑制抖振的能力. 1 AUV 数学模型及其线性化 为了便于控制系统的分析与设计,通常将 AUV 六自由度运动分解为垂直面运动和水平面运动,本 文只研究 AUV 在垂直面内的姿态控制.由于 AUV 姿态控制可以看作受到扰动作用后在平衡位置附近 做小幅度运动,因此基于小扰动法对其垂直面模型 做线性化处理[6] ,得到[2] : m - Z·w - Z·q 0 0 - M·w Iyy - M·q 0 0 0 0 1 0 0 0 0 1 é ë ê ê ê ê ê ê ù û ú ú ú ú ú ú w · q · θ · z · é ë ê ê ê ê ê ê ù û ú ú ú ú ú ú = Zuw u (Zuq + m)u 0 0 Muw u Muqu 0 0 0 1 0 0 1 0 - u 0 é ë ê ê ê ê ê ê ù û ú ú ú ú ú ú w q θ z é ë ê ê ê ê ê ù û ú ú ú ú ú + Zuuδu 2 Muuδu 2 0 0 é ë ê ê ê ê ê ê ù û ú ú ú ú ú ú δ. 式中:m 为 AUV 质量;I 为转动惯量;Z 和 M 为水动 力系数[6] ; z 、 θ 分别为深度和纵摇角;u、w 和 q 分 别为纵荡速度、升沉速度和纵摇角速度; δ 为水平舵 角.取轴向速度为 2 m / s,基于某典型 AUV 水动力系 数建立系统标称状态方程为[2] w · q · θ · z · é ë ê ê ê ê ê ê ù û ú ú ú ú ú ú = - 1.040 0.865 - 0.020 0 6.000 - 0.681 0.708 0 0 1.000 0 0 1.000 0 - 2.000 0 é ë ê ê ê ê ê ù û ú ú ú ú ú w q θ z é ë ê ê ê ê ê ù û ú ú ú ú ú + -0.072 -0.722 0 0 é ë ê ê ê ê ê ù û ú ú ú ú ú δ. (1) 考虑到模型的不确定性,设所有相关水动力系 数有 30%的相对不确定度[2] , p 为水动力系数标称 值, p1 和 p2 分别为水动力系数下限值和上限值: p1 = 0.7p, p2 { = 1.3p. 实际水动力系数将在 p1 和 p2 之间变化,进而可 以得到系统状态方程的下限形式和上限形式. 基于水动力系数 p1 的系统状态方程为[2] w · q · θ · z · é ë ê ê ê ê ê ê ù û ú ú ú ú ú ú = - 0.950 1.150 - 0.021 0 9.280 - 0.615 0.858 0 0 1.000 0 0 1.000 0 - 2.000 0 é ë ê ê ê ê ê ù û ú ú ú ú ú w q θ z é ë ê ê ê ê ê ù û ú ú ú ú ú + -0.063 -0.615 0 0 é ë ê ê ê ê ê ù û ú ú ú ú ú δ. (2) 基于水动力系数 p2 的系统状态方程为[2] w · q · θ · z · é ë ê ê ê ê ê ê ê ù û ú ú ú ú ú ú ú = - 1.190 0.730 - 0.020 0 6.680 - 0.718 0.603 0 0 1.000 0 0 1.000 0 - 2.000 0 é ë ê ê ê ê ê ù û ú ú ú ú ú w q θ z é ë ê ê ê ê ê ù û ú ú ú ú ú + -0.078 -0.796 0 0 é ë ê ê ê ê ê ù û ú ú ú ú ú δ. (3) 2 控制方法 基于切换模糊化的滑模变结构 AUV 姿态控制 方法的原理框图如图 1 所示. 图 1 控制方法原理框图 Fig.1 Block diagram of the control method 图 1 中, Zd 、 θd 为期望深度和纵摇角,即平衡状 态, Z、 θ 为实际深度和纵摇角; δ 为水平舵角. 2.1 滑模变结构控制 针对如下线性系统: x · = Ax + B(u + f(t)), s = Cx. { (4) 式中:A 和 B 取自式(1),容易验证(A,B) 完全能 控,因 此 系 统 可 以 任 意 配 置 极 点[7] , 本 文 采 用 第 6 期 郝阳,等:基于切换模糊化的滑模变结构 AUV 姿态控制 ·533·

.534. 智能系统学报 第8卷 Ackermann公式设计切换函数s=Cx中的C值: NB Nm NS ZO PS PM PB 1. C=[0.01][BABA-B]-P(A). 0.8 式中:P(A)为期望特征多项式复变量s换成A所得 0.6 的矩阵多项式[],得 国 C=[0.7970-1.4645-1.72900.4113]. 0.2 滑模变结构控制器的设计通常采用趋近律形式,如 指数趋近律: 切换函数 slaw =s =-ssgn(s)-ks. (5) 图3输出变量隶属函数 式中:g=0.3,k=0.5. Fig.3 Membership function of out put variable 本文使用模糊控制器的输出代替其中的切换 项,得到基于切换模糊化的趋近律: 3 仿真结果 slaw ==-sFuzzy(s)-ks. (6) 仿真条件统一设定为AUV因受到小扰动f(t)作 式中:e=3,k=5,Fuzy(s)为模糊控制的输出. 用而在平衡状态(wu=0m/s,9a=0rad/s,0。=0rad, 将式(5)和(6)代入状态方程(4)可分别得到 z4=0)附近进行小幅度运动,设其初始状态为:心。= 滑模变结构控制律和基于切换模糊化的滑模变结构 0.01m/s,q。=0.02rad/s,0。=0.05rad,z。=0.5m. 控制律,它们的表示形式为[例 3.1标称系统仿真 u=(CB)(-CAx slaw). 通过不同控制器对式(1)所示AUV标称系统 式中:f(t)为扰动项,表示正态分布的随机小扰动 模型进行仿真对比,论证本文提出方法具有较好的 2.2模糊控制 控制效果和较强的削弱抖振及抗干扰能力.滑模变 该模糊控制为单输入单输出,其输入与输出的 结构控制和切换模糊化的滑模变结构控制的深度响 论域分别为 应曲线如图4所示,可以看到二者都能以较快的响 A=(A;I NB,NM,NS,ZO,PS,PM,PB) 应速度到达平衡位置,基本没有稳态误差,且都 B=(B,I NB,NM,NS,ZO,PS,PM,PB) 具有一定的抗干扰能力。 式中:NB为负大,NM为负中,NS为负小,ZE为零, 0.5 …滑模变结构控制 PS为正小,PM为正中,PB为正大.输入、输出量的 0.4 切换模糊化的滑 取值为[-3,3]其模糊规则为 模变结构控制 0.3 If A =A;then B=Bi. 其控制效果主要依赖于隶属函数和清晰化方法 0.1 的选取,经过反复试验,确定其输入与输出的隶属函 数如图2、3所示.采用(最大隶属度)平均值法实现 输出量的清晰化[1o -0.1 0 1015202530 1.0B NM NS ZO PS PM PB tis 图42种控制方法的深度响应 0.8 Fig.4 Depth response curve of 2 control methods 06 滑模变结构控制和切换模糊化的滑模变结构控 #0.4 制的纵摇响应曲线如图5和图6所示,可以看到二 0.2 者响应速度基本相同,但切换模糊化的滑模变结构 0 控制纵摇响应输出更加平滑,控制效果更好.滑模变 切换函数 结构控制和切换模糊化的滑模变结构控制的舵角响 图2输入变量隶属函数 应曲线如图7和图8所示,可以看到切换模糊化的 Fig.2 Membership function of input variable 滑模变结构控制器能够有效降低抖振
Ackermann 公式设计切换函数 s =Cx 中的 C 值: C= [0 ... 0 1] B AB ... A n-1 [ B] -1 P(A). 式中:P(A)为期望特征多项式复变量 s 换成 A 所得 的矩阵多项式[8-9] ,得 C = [0.7970 - 1.4645 - 1.7290 0.4113]. 滑模变结构控制器的设计通常采用趋近律形式,如 指数趋近律: slaw = s · = - εsgn(s) - ks. (5) 式中: ε = 0.3, k = 0.5. 本文使用模糊控制器的输出代替其中的切换 项,得到基于切换模糊化的趋近律: slaw = s · = - εFuzzy(s) - ks. (6) 式中: ε = 3, k = 5, Fuzzy(s) 为模糊控制的输出. 将式(5)和(6) 代入状态方程(4) 可分别得到 滑模变结构控制律和基于切换模糊化的滑模变结构 控制律,它们的表示形式为[9] u = (CB) -1 ( - CAx + slaw). 式中: f(t) 为扰动项,表示正态分布的随机小扰动. 2.2 模糊控制 该模糊控制为单输入单输出,其输入与输出的 论域分别为 A = Ai { | NB,NM,NS,ZO,PS,PM,PB} , B = Bi { | NB,NM,NS,ZO,PS,PM,PB} . 式中:NB 为负大,NM 为负中, NS 为负小,ZE 为零, PS 为正小,PM 为正中,PB 为正大.输入、输出量的 取值为[-3,3].其模糊规则为 If A = Ai then B = Bi . 其控制效果主要依赖于隶属函数和清晰化方法 的选取,经过反复试验,确定其输入与输出的隶属函 数如图 2、3 所示.采用(最大隶属度)平均值法实现 输出量的清晰化[10] . 图 2 输入变量隶属函数 Fig.2 Membership function of input variable 图 3 输出变量隶属函数 Fig.3 Membership function of out put variable 3 仿真结果 仿真条件统一设定为 AUV 因受到小扰动 f(t) 作 用而在平衡状态( wd =0 m/ s, qd =0 rad/ s, θd =0 rad, zd =0)附近进行小幅度运动,设其初始状态为: wo = 0.01 m/ s, qo =0.02 rad/ s, θo =0.05 rad, zo =0.5 m. 3.1 标称系统仿真 通过不同控制器对式(1) 所示 AUV 标称系统 模型进行仿真对比,论证本文提出方法具有较好的 控制效果和较强的削弱抖振及抗干扰能力.滑模变 结构控制和切换模糊化的滑模变结构控制的深度响 应曲线如图 4 所示,可以看到二者都能以较快的响 应速度到达平衡位置 zd ,基本没有稳态误差,且都 具有一定的抗干扰能力. 图 4 2 种控制方法的深度响应 Fig.4 Depth response curve of 2 control methods 滑模变结构控制和切换模糊化的滑模变结构控 制的纵摇响应曲线如图 5 和图 6 所示,可以看到二 者响应速度基本相同,但切换模糊化的滑模变结构 控制纵摇响应输出更加平滑,控制效果更好.滑模变 结构控制和切换模糊化的滑模变结构控制的舵角响 应曲线如图 7 和图 8 所示,可以看到切换模糊化的 滑模变结构控制器能够有效降低抖振. ·534· 智 能 系 统 学 报 第 8 卷
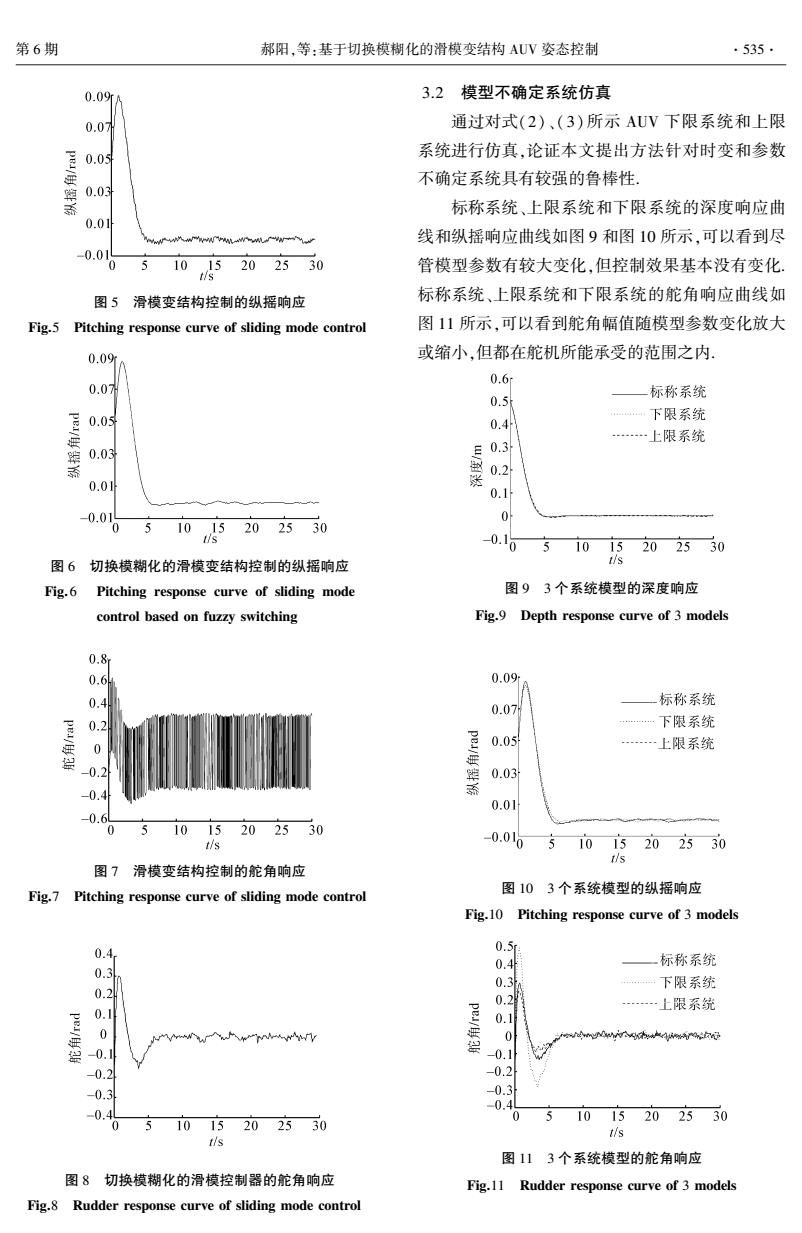
第6期 郝阳,等:基于切换模糊化的滑模变结构AUV姿态控制 .535. 0.09N 3.2模型不确定系统仿真 0.0 通过对式(2)、(3)所示AUV下限系统和上限 系统进行仿真,论证本文提出方法针对时变和参数 0.05 不确定系统具有较强的鲁棒性, 0.03 标称系统、上限系统和下限系统的深度响应曲 0.01 线和纵摇响应曲线如图9和图10所示,可以看到尽 0.0 0 5 105 202530 管模型参数有较大变化,但控制效果基本没有变化 图5滑模变结构控制的纵摇响应 标称系统、上限系统和下限系统的舵角响应曲线如 Fig.5 Pitching response curve of sliding mode control 图11所示,可以看到舵角幅值随模型参数变化放大 0.09% 或缩小,但都在舵机所能承受的范围之内。 0.6 0.07 标称系统 0.5 0.05 下限系统 0.4 …上限系统 0.03 0.2 0.0 0.1 0.01 0 0 5 1015202530 t/s 0.10 1015202530 图6切换模糊化的滑模变结构控制的纵摇响应 t/s Fig.6 Pitching response curve of sliding mode 图93个系统模型的深度响应 control based on fuzzy switching Fig.9 Depth response curve of 3 models 0.8 0.6 0.09 0.4 标称系统 0.07 0.2 下限系统 0 0.05 …上限系统 0.2 0.03 -0.4 系 0.0 -0.6 5 1015202530 t/s 0.010 1015202530 t/s 图7滑模变结构控制的舵角响应 Fig.7 Pitching response curve of sliding mode control 图103个系统模型的纵摇响应 Fig.10 Pitching response curve of 3 models 0.4 0.5r 0.4 标称系统 0.3 0.3 下限系统 0.2 0.2 …上限系统 0.1 0 0 -0.1 0.2 -0.2 -0.3 -0.3 -0.4 -0.4 0 1015202530 0 51015 202530 5 t/s tis 图113个系统模型的舵角响应 图8切换模糊化的滑模控制器的舵角响应 Fig.11 Rudder response curve of 3 models Fig.8 Rudder response curve of sliding mode control
图 5 滑模变结构控制的纵摇响应 Fig.5 Pitching response curve of sliding mode control 图 6 切换模糊化的滑模变结构控制的纵摇响应 Fig. 6 Pitching response curve of sliding mode control based on fuzzy switching 图 7 滑模变结构控制的舵角响应 Fig.7 Pitching response curve of sliding mode control 图 8 切换模糊化的滑模控制器的舵角响应 Fig.8 Rudder response curve of sliding mode control 3.2 模型不确定系统仿真 通过对式(2)、(3)所示 AUV 下限系统和上限 系统进行仿真,论证本文提出方法针对时变和参数 不确定系统具有较强的鲁棒性. 标称系统、上限系统和下限系统的深度响应曲 线和纵摇响应曲线如图 9 和图 10 所示,可以看到尽 管模型参数有较大变化,但控制效果基本没有变化. 标称系统、上限系统和下限系统的舵角响应曲线如 图 11 所示,可以看到舵角幅值随模型参数变化放大 或缩小,但都在舵机所能承受的范围之内. 图 9 3 个系统模型的深度响应 Fig.9 Depth response curve of 3 models 图 10 3 个系统模型的纵摇响应 Fig.10 Pitching response curve of 3 models 图 11 3 个系统模型的舵角响应 Fig.11 Rudder response curve of 3 models 第 6 期 郝阳,等:基于切换模糊化的滑模变结构 AUV 姿态控制 ·535·

.536. 智能系统学报 第8卷 SHEN Jiansen,ZHOU Xuchang,GAO Xuan.Fuzzy sliding 结束语 mode control for near-surface AUV in longitudinal plane[J]. 本文不同于以往研究工作中直接由模糊控制器 Torpedo Technology,2011,19(5):360-364. 输出变结构控制律或其变化率的方法,使用模糊控 [5]阚如文.无人水下航行器姿态控制策略研究[D].长春: 制输出连续非线性控制信号,改变滑模变结构控制 吉林大学,2012:33-46. 在本质上不连续的开关特性来解决抖振问题:在有 KAN Ruwen.Research on attitude control strategies of un- manned underwater vehicle[D].Changchun:Jilin Universi- 效降低抖振的同时具有较好的控制效果、较强的鲁 y,2012:33-46. 棒性和抗干扰能力,能够很好地适应AUV控制系统 [6]金鸿章,姚绪梁.船舶控制原理[M].哈尔滨:哈尔滨工程 设计的需要.未来可以在其参数确定中引入自适应 大学出版社,2001:1-13. 调节方法,以进一步提高控制系统性能,并最终使用 [7]郑大钟线性系统理论[M]2版北京:清华大学出版社, 该方法设计控制器应用于实际AUV控制系统, 2002:135-209. [8]彭亚为,杜彬,陈娟.基于Ackermann公式的滑模控制设 参考文献: 计方法[J].北京化工大学学报:自然科学版,2011,38 [1]SHI Xiaocheng,ZHOU Jiajia,BIAN Xinqian,et al.Fuzzy (4):128-133. sliding-mode controller for the motion of autonomous under- PENG Yawei,DU Bin,CHEN Juan.Method of sliding water vehicle[C]//Proceedings of IEEE International Con- mode control design base on Ackermann formula[J].Jour- ference on Mechatronics and Automation.Takamatsu,Ja- nal of Beijing University of Chemical Technology:Natural pan,2008:466-470. Science,2011,38(4):128-133. [2]魏英杰,毕凤阳,张家钟,等.时滞时变AUV的模糊变结 [9]刘金琨.滑模变结构控制MATLAB仿真[M].北京:清华 构控制[J刀].系统工程与电子技术,2009,31(8):1949 大学出版社,2005:22-40. 1953 [10]石辛民,郝整清.模糊控制及其MATLAB仿真[M].北 WEI Yingjie,BI Fengyang,ZHANG Jiazhong,et al.Fuzzy 京:清华大学出版社,2008:11-51 sliding mode controller for time delay and time varying au- 作者简介: tonomous underwater vehicles[J].Systems Engineering and 郝阳,男,1980年生,工程师,主要 Electronics,2009,31(8):1949-1953. 研究方向为先进控制理论及应用。 [3]毕凤阳,张家钟,魏英杰,等.模型不确定时滞欠驱动 AUV的模糊变结构控制[J].哈尔滨工业大学学报, 2010,42(3):358-363. BI Fengyang,ZHANG Jiazhong,WEI Yingjie,et al.A 赵新华,女,1980年生,讲师,硕士 研究生导师,主要研究方向为超空泡航 fuzzy sliding mode controller for underactuated autonomous underwater vehicles with uncertain time delay[J].Journal of 行体、AUV的动力学及智能控制,发表 学术论文10余篇,均被EI检索. Harbin Institute of Technology,2010,42(3):358-363. [4]沈建森,周徐昌,高璇远程AUV近水面运动纵向模糊滑 模控制[J刀.鱼雷技术,2011,19(5):360-364
4 结束语 本文不同于以往研究工作中直接由模糊控制器 输出变结构控制律或其变化率的方法,使用模糊控 制输出连续非线性控制信号,改变滑模变结构控制 在本质上不连续的开关特性来解决抖振问题;在有 效降低抖振的同时具有较好的控制效果、较强的鲁 棒性和抗干扰能力,能够很好地适应 AUV 控制系统 设计的需要.未来可以在其参数确定中引入自适应 调节方法,以进一步提高控制系统性能,并最终使用 该方法设计控制器应用于实际 AUV 控制系统. 参考文献: [1]SHI Xiaocheng, ZHOU Jiajia, BIAN Xinqian, et al. Fuzzy sliding-mode controller for the motion of autonomous under⁃ water vehicle[C] / / Proceedings of IEEE International Con⁃ ference on Mechatronics and Automation. Takamatsu, Ja⁃ pan, 2008: 466⁃470. [2]魏英杰,毕凤阳,张家钟,等.时滞时变 AUV 的模糊变结 构控制[ J].系统工程与电子技术, 2009, 31(8): 1949⁃ 1953. WEI Yingjie, BI Fengyang, ZHANG Jiazhong, et al. Fuzzy sliding mode controller for time delay and time varying au⁃ tonomous underwater vehicles[ J]. Systems Engineering and Electronics, 2009, 31(8): 1949⁃1953. [3]毕凤阳,张家钟,魏英杰,等. 模型不确定时滞欠驱动 AUV 的模糊变结构控制 [ J]. 哈尔滨工业大学学报, 2010, 42(3): 358⁃363. BI Fengyang, ZHANG Jiazhong, WEI Yingjie, et al. A fuzzy sliding mode controller for underactuated autonomous underwater vehicles with uncertain time delay[J]. Journal of Harbin Institute of Technology, 2010, 42(3): 358⁃363. [4]沈建森,周徐昌,高璇.远程 AUV 近水面运动纵向模糊滑 模控制[J].鱼雷技术, 2011, 19(5): 360⁃364. SHEN Jiansen, ZHOU Xuchang, GAO Xuan. Fuzzy sliding mode control for near⁃surface AUV in longitudinal plane[J]. Torpedo Technology, 2011, 19(5): 360⁃364. [5]阚如文.无人水下航行器姿态控制策略研究[D].长春: 吉林大学, 2012: 33⁃46. KAN Ruwen. Research on attitude control strategies of un⁃ manned underwater vehicle[D]. Changchun: Jilin Universi⁃ ty, 2012: 33⁃46. [6]金鸿章,姚绪梁.船舶控制原理[M].哈尔滨:哈尔滨工程 大学出版社, 2001: 1⁃13. [7]郑大钟.线性系统理论[M].2 版.北京:清华大学出版社, 2002: 135⁃209. [8]彭亚为,杜彬,陈娟.基于 Ackermann 公式的滑模控制设 计方法[J].北京化工大学学报: 自然科学版, 2011, 38 (4): 128⁃133. PENG Yawei, DU Bin, CHEN Juan. Method of sliding mode control design base on Ackermann formula[ J]. Jour⁃ nal of Beijing University of Chemical Technology: Natural Science, 2011, 38(4): 128⁃133. [9]刘金琨.滑模变结构控制 MATLAB 仿真[M].北京: 清华 大学出版社, 2005: 22⁃40. [10]石辛民,郝整清.模糊控制及其 MATLAB 仿真[M].北 京: 清华大学出版社, 2008: 11⁃51. 作者简介: 郝阳,男,1980 年生,工程师,主要 研究方向为先进控制理论及应用. 赵新华,女,1980 年生,讲师,硕士 研究生导师,主要研究方向为超空泡航 行体、AUV 的动力学及智能控制,发表 学术论文 10 余篇,均被 EI 检索. ·536· 智 能 系 统 学 报 第 8 卷