智能系统：PI参数混合整定法在闭环矢量控制系统中的应用

第8卷第5期 智能系统学报 Vol.8 No.5 2013年10月 CAAI Transactions on Intelligent Systems 0ct.2013 D0:10.3969/j.issn.1673-4785.201209043 网络出版地址：http://www.enki..net/kcms/detail/23.1538.TP.20130515.0937.009.html PI参数混合整定法在闭环矢量控制系统中的应用 李鹏，王胜勇，卢家斌，黄心汉2 (1.中治南方（武汉）自动化有限公司研发部，湖北武汉430205：2.华中科技大学控制科学与工程系，湖北武汉 430074) 摘要：为使闭环矢量控制系统工作在最佳状态，提出了基于模型的离线式整定与模糊PI在线整定相结合的混合整 定法.该方法首先根据矢量控制原理推导出系统的数学模型，采用恒转矩启动并自由停机的方法计算出转动惯量然 后根据数学模型计算PI参数和内环补偿量，构建了模糊PI控制器，提出了新的PI控制规则表最后的对比实验表 明，PI参数混合整定法提高了系统的动态性能和稳态精度，优于仅采用单一整定法的系统，验证了方法的有效性。 关键词：PI参数；PI参数整定；矢量控制：闭环矢量控制；模糊控制 中图分类号：TP29文献标志码：A文章编号：1673-4785(2013)05-0446-07 中文引用格式：李鹅，王胜勇，卢家斌，等.PI参数混合整定法在闭环矢量控制系统中的应用[J].智能系统学报，2013,8(5)：446452. 英文引用格式：LI Peng,WANG Shengyong,LU Jiabin,etal.The application of hybrid PI parameters tunning method to the closed-loop vector control system[J].CAAI Transactions on Intelligent Systems,2013,8(5):446-452. The application of hybrid PI parameters tunning method to the closed-loop vector control system LI Peng',WANG Shengyong',LU Jiabin',HUANG Xinhan2 (1.Research Department,WISDRI (Wuhan)Automation Co.,Ltd,Wuhan 430205,China;2.Department of Control Science and Engineering,Huazhong University of Science and Technology,Wuhan 430074,China) Abstract:In order to make closed-loop vector control system work in the best status,a hybrid tuning method was introduced,which combines a model-based offline tuning method with a fuzzy PI online tuning method.First of all, the mathematical model of the system was constructed in accordance to the vector control theory,and the moment of inertia was calculated using the method of a constant-torque startup and freely stopping system.After that the PI pa- rameters and the inner loop compensations were calculated according to the mathematical model.Next,a fuzzy PI controller was structured,and the new PI control rule forms were put forward.The final contrastive experiments in- dicate that the hybrid PI parameters tuning method improves the dynamic performance and the steady-state precision of the system,and it is better than the system which only adopts a single tuning method.The validity of the method was justified. Keywords:PI parameters;PI parameters tuning;vector control;closed-loop vector control;fuzzy control PD控制是迄今为止最通用的控制算法」 在对异步交流电机的控制中，通常采用矢量控 1915一1940年PD控制器经历了从产生到普及的 制与PID控制器相结合的方式，PD的参数整定可 过程，推动了工业的极大进步.尽管自1940年至今， 分为离线式和在线式2种.离线式整定完全基于系 大量的专家学者提出了许多先进控制方法，但PD 统模型，但交流电机模型复杂，难以构建精确模型； 控制器以其结构简单、计算量小、易于实现、鲁棒性 在线式整定一般采用智能算法，如模糊算法[34]、神 强等诸多优点，仍被广泛应用于冶金、化工、电力和 经网络[56等，不依赖系统模型，但容易陷入局部最 机械等各种工业过程控制中[。 优值.当前许多应用中基本都采用较为简单且易实 现的在线整定，不用花费大量精力构建系统数学模 收稿日期：2012-09-20.网络出版日期：2013-05-15. 通信作者：李鹏.E-mail:98504@wisdri.com 型，因此整定效果有限[9).目前比较流行且有效的

第 ８ 卷第 ５ 期 智 能 系 统 学 报 Ｖｏｌ.８ №.５ ２０１３ 年 １０ 月 ＣＡＡＩ Ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ Ｉｎｔｅｌｌｉｇｅｎｔ Ｓｙｓｔｅｍｓ Ｏｃｔ. ２０１３ ＤＯＩ:１０.３９６９ / ｊ.ｉｓｓｎ.１６７３￣４７８５.２０１２０９０４３ 网络出版地址:ｈｔｔｐ: / / ｗｗｗ.ｃｎｋｉ.ｎｅｔ / ｋｃｍｓ/ ｄｅｔａｉｌ / ２３.１５３８.ＴＰ.２０１３０５１５.０９３７.００９.ｈｔｍｌ ＰＩ 参数混合整定法在闭环矢量控制系统中的应用 李鹏１ ꎬ王胜勇１ ꎬ卢家斌１ ꎬ黄心汉２ (１.中冶南方(武汉)自动化有限公司 研发部ꎬ湖北 武汉 ４３０２０５ꎻ ２.华中科技大学 控制科学与工程系ꎬ湖北 武汉 ４３００７４) 摘 要:为使闭环矢量控制系统工作在最佳状态ꎬ提出了基于模型的离线式整定与模糊 ＰＩ 在线整定相结合的混合整 定法.该方法首先根据矢量控制原理推导出系统的数学模型ꎬ采用恒转矩启动并自由停机的方法计算出转动惯量.然 后根据数学模型计算 ＰＩ 参数和内环补偿量ꎬ构建了模糊 ＰＩ 控制器ꎬ提出了新的 ＰＩ 控制规则表.最后的对比实验表 明ꎬＰＩ 参数混合整定法提高了系统的动态性能和稳态精度ꎬ优于仅采用单一整定法的系统ꎬ验证了方法的有效性. 关键词:ＰＩ 参数ꎻＰＩ 参数整定ꎻ矢量控制ꎻ闭环矢量控制ꎻ模糊控制 中图分类号:ＴＰ２９ 文献标志码:Ａ 文章编号:１６７３￣４７８５(２０１３)０５￣０４４６￣０７ 中文引用格式:李鹏ꎬ王胜勇ꎬ卢家斌ꎬ等.ＰＩ 参数混合整定法在闭环矢量控制系统中的应用[Ｊ].智能系统学报ꎬ ２０１３ꎬ ８(５): ４４６￣４５２. 英文引用格式:ＬＩ Ｐｅｎｇꎬ ＷＡＮＧ Ｓｈｅｎｇｙｏｎｇꎬ ＬＵ Ｊｉａｂｉｎꎬ ｅｔ ａｌ. Ｔｈｅ ａｐｐｌｉｃａｔｉｏｎ ｏｆ ｈｙｂｒｉｄ ＰＩ ｐａｒａｍｅｔｅｒｓ ｔｕｎｎｉｎｇ ｍｅｔｈｏｄ ｔｏ ｔｈｅ ｃｌｏｓｅｄ￣ｌｏｏｐ ｖｅｃｔｏｒ ｃｏｎｔｒｏｌ ｓｙｓｔｅｍ[Ｊ]. ＣＡＡＩ Ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ Ｉｎｔｅｌｌｉｇｅｎｔ Ｓｙｓｔｅｍｓꎬ ２０１３ꎬ ８(５): ４４６￣４５２. Ｔｈｅ ａｐｐｌｉｃａｔｉｏｎ ｏｆ ｈｙｂｒｉｄ ＰＩ ｐａｒａｍｅｔｅｒｓ ｔｕｎｎｉｎｇ ｍｅｔｈｏｄ ｔｏ ｔｈｅ ｃｌｏｓｅｄ￣ｌｏｏｐ ｖｅｃｔｏｒ ｃｏｎｔｒｏｌ ｓｙｓｔｅｍ ＬＩ Ｐｅｎｇ １ ꎬ ＷＡＮＧ Ｓｈｅｎｇｙｏｎｇ １ ꎬ ＬＵ Ｊｉａｂｉｎ １ ꎬ ＨＵＡＮＧ Ｘｉｎｈａｎ ２ (１. Ｒｅｓｅａｒｃｈ Ｄｅｐａｒｔｍｅｎｔꎬ ＷＩＳＤＲＩ (Ｗｕｈａｎ) Ａｕｔｏｍａｔｉｏｎ Ｃｏ.ꎬ Ｌｔｄꎬ Ｗｕｈａｎ ４３０２０５ꎬ Ｃｈｉｎａꎻ ２. Ｄｅｐａｒｔｍｅｎｔ ｏｆ Ｃｏｎｔｒｏｌ Ｓｃｉｅｎｃｅ ａｎｄ Ｅｎｇｉｎｅｅｒｉｎｇꎬ Ｈｕａｚｈｏｎｇ Ｕｎｉｖｅｒｓｉｔｙ ｏｆ Ｓｃｉｅｎｃｅ ａｎｄ Ｔｅｃｈｎｏｌｏｇｙꎬ Ｗｕｈａｎ ４３００７４ꎬ Ｃｈｉｎａ) Ａｂｓｔｒａｃｔ:Ｉｎ ｏｒｄｅｒ ｔｏ ｍａｋｅ ｃｌｏｓｅｄ￣ｌｏｏｐ ｖｅｃｔｏｒ ｃｏｎｔｒｏｌ ｓｙｓｔｅｍ ｗｏｒｋ ｉｎ ｔｈｅ ｂｅｓｔ ｓｔａｔｕｓꎬ ａ ｈｙｂｒｉｄ ｔｕｎｉｎｇ ｍｅｔｈｏｄ ｗａｓ ｉｎｔｒｏｄｕｃｅｄꎬ ｗｈｉｃｈ ｃｏｍｂｉｎｅｓ ａ ｍｏｄｅｌ￣ｂａｓｅｄ ｏｆｆｌｉｎｅ ｔｕｎｉｎｇ ｍｅｔｈｏｄ ｗｉｔｈ ａ ｆｕｚｚｙ ＰＩ ｏｎｌｉｎｅ ｔｕｎｉｎｇ ｍｅｔｈｏｄ. Ｆｉｒｓｔ ｏｆ ａｌｌꎬ ｔｈｅ ｍａｔｈｅｍａｔｉｃａｌ ｍｏｄｅｌ ｏｆ ｔｈｅ ｓｙｓｔｅｍ ｗａｓ ｃｏｎｓｔｒｕｃｔｅｄ ｉｎ ａｃｃｏｒｄａｎｃｅ ｔｏ ｔｈｅ ｖｅｃｔｏｒ ｃｏｎｔｒｏｌ ｔｈｅｏｒｙꎬ ａｎｄ ｔｈｅ ｍｏｍｅｎｔ ｏｆ ｉｎｅｒｔｉａ ｗａｓ ｃａｌｃｕｌａｔｅｄ ｕｓｉｎｇ ｔｈｅ ｍｅｔｈｏｄ ｏｆ ａ ｃｏｎｓｔａｎｔ￣ｔｏｒｑｕｅ ｓｔａｒｔｕｐ ａｎｄ ｆｒｅｅｌｙ ｓｔｏｐｐｉｎｇ ｓｙｓｔｅｍ. Ａｆｔｅｒ ｔｈａｔ ｔｈｅ ＰＩ ｐａ￣ ｒａｍｅｔｅｒｓ ａｎｄ ｔｈｅ ｉｎｎｅｒ ｌｏｏｐ ｃｏｍｐｅｎｓａｔｉｏｎｓ ｗｅｒｅ ｃａｌｃｕｌａｔｅｄ ａｃｃｏｒｄｉｎｇ ｔｏ ｔｈｅ ｍａｔｈｅｍａｔｉｃａｌ ｍｏｄｅｌ. Ｎｅｘｔꎬ ａ ｆｕｚｚｙ ＰＩ ｃｏｎｔｒｏｌｌｅｒ ｗａｓ ｓｔｒｕｃｔｕｒｅｄꎬ ａｎｄ ｔｈｅ ｎｅｗ ＰＩ ｃｏｎｔｒｏｌ ｒｕｌｅ ｆｏｒｍｓ ｗｅｒｅ ｐｕｔ ｆｏｒｗａｒｄ. Ｔｈｅ ｆｉｎａｌ ｃｏｎｔｒａｓｔｉｖｅ ｅｘｐｅｒｉｍｅｎｔｓ ｉｎ￣ ｄｉｃａｔｅ ｔｈａｔ ｔｈｅ ｈｙｂｒｉｄ ＰＩ ｐａｒａｍｅｔｅｒｓ ｔｕｎｉｎｇ ｍｅｔｈｏｄ ｉｍｐｒｏｖｅｓ ｔｈｅ ｄｙｎａｍｉｃ ｐｅｒｆｏｒｍａｎｃｅ ａｎｄ ｔｈｅ ｓｔｅａｄｙ￣ｓｔａｔｅ ｐｒｅｃｉｓｉｏｎ ｏｆ ｔｈｅ ｓｙｓｔｅｍꎬ ａｎｄ ｉｔ ｉｓ ｂｅｔｔｅｒ ｔｈａｎ ｔｈｅ ｓｙｓｔｅｍ ｗｈｉｃｈ ｏｎｌｙ ａｄｏｐｔｓ ａ ｓｉｎｇｌｅ ｔｕｎｉｎｇ ｍｅｔｈｏｄ. Ｔｈｅ ｖａｌｉｄｉｔｙ ｏｆ ｔｈｅ ｍｅｔｈｏｄ ｗａｓ ｊｕｓｔｉｆｉｅｄ. Ｋｅｙｗｏｒｄｓ:ＰＩ ｐａｒａｍｅｔｅｒｓꎻ ＰＩ ｐａｒａｍｅｔｅｒｓ ｔｕｎｉｎｇꎻ ｖｅｃｔｏｒ ｃｏｎｔｒｏｌꎻ ｃｌｏｓｅｄ￣ｌｏｏｐ ｖｅｃｔｏｒ ｃｏｎｔｒｏｌꎻ ｆｕｚｚｙ ｃｏｎｔｒｏｌ 收稿日期:２０１２￣０９￣２０. 网络出版日期:２０１３￣０５￣１５. 通信作者:李鹏. Ｅ￣ｍａｉｌ: ９８５０４＠ ｗｉｓｄｒｉ.ｃｏｍ. ＰＩＤ 控 制 是 迄 今 为 止 最 通 用 的 控 制 算 法. １９１５—１９４０ 年 ＰＩＤ 控制器经历了从产生到普及的 过程ꎬ推动了工业的极大进步.尽管自 １９４０ 年至今ꎬ 大量的专家学者提出了许多先进控制方法ꎬ但 ＰＩＤ 控制器以其结构简单、计算量小、易于实现、鲁棒性 强等诸多优点ꎬ仍被广泛应用于冶金、化工、电力和 机械等各种工业过程控制中[１￣２] . 在对异步交流电机的控制中ꎬ通常采用矢量控 制与 ＰＩＤ 控制器相结合的方式ꎬＰＩＤ 的参数整定可 分为离线式和在线式 ２ 种.离线式整定完全基于系 统模型ꎬ但交流电机模型复杂ꎬ难以构建精确模型ꎻ 在线式整定一般采用智能算法ꎬ如模糊算法[３￣４] 、神 经网络[５￣６]等ꎬ不依赖系统模型ꎬ但容易陷入局部最 优值.当前许多应用中基本都采用较为简单且易实 现的在线整定ꎬ不用花费大量精力构建系统数学模 型ꎬ因此整定效果有限[７￣９] .目前比较流行且有效的

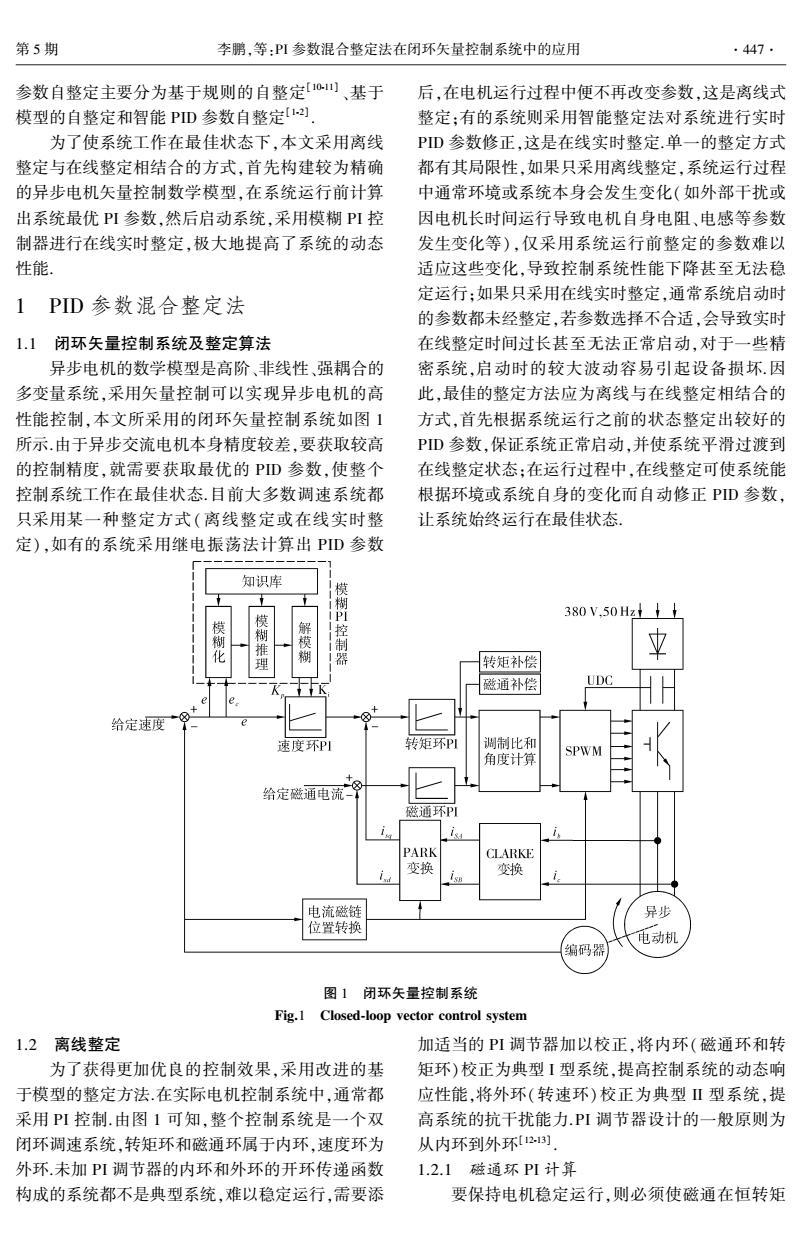
第5期 李鹏，等：PI参数混合整定法在闭环矢量控制系统中的应用 .447. 参数自整定主要分为基于规则的自整定[0山、基于 后，在电机运行过程中便不再改变参数，这是离线式 模型的自整定和智能PD参数自整定以 整定：有的系统则采用智能整定法对系统进行实时 为了使系统工作在最佳状态下，本文采用离线 PD参数修正，这是在线实时整定.单一的整定方式 整定与在线整定相结合的方式，首先构建较为精确 都有其局限性，如果只采用离线整定，系统运行过程 的异步电机矢量控制数学模型，在系统运行前计算 中通常环境或系统本身会发生变化（如外部干扰或 出系统最优PI参数，然后启动系统，采用模糊PI控 因电机长时间运行导致电机自身电阻、电感等参数 制器进行在线实时整定，极大地提高了系统的动态 发生变化等)，仅采用系统运行前整定的参数难以 性能， 适应这些变化，导致控制系统性能下降甚至无法稳 定运行：如果只采用在线实时整定，通常系统启动时 1PID参数混合整定法 的参数都未经整定，若参数选择不合适，会导致实时 1.1闭环矢量控制系统及整定算法 在线整定时间过长甚至无法正常启动，对于一些精 异步电机的数学模型是高阶、非线性、强耦合的 密系统，启动时的较大波动容易引起设备损坏因 多变量系统，采用矢量控制可以实现异步电机的高 此，最佳的整定方法应为离线与在线整定相结合的 性能控制，本文所采用的闭环矢量控制系统如图1 方式，首先根据系统运行之前的状态整定出较好的 所示.由于异步交流电机本身精度较差，要获取较高 PD参数，保证系统正常启动，并使系统平滑过渡到 的控制精度，就需要获取最优的PD参数，使整个 在线整定状态：在运行过程中，在线整定可使系统能 控制系统工作在最佳状态.目前大多数调速系统都 根据环境或系统自身的变化而自动修正PD参数， 只采用某一种整定方式（离线整定或在线实时整 让系统始终运行在最佳状态， 定)，如有的系统采用继电振荡法计算出PID参数 知识库 模 380V,50Hz 模制化 模糊推理 解模糊 控制器 转矩补偿 磁通补偿 UDC 给定速度 速度环PI 转矩环P 调制比和 角度计算 SPWM 区 给定磁通电流 磁通环P川 PARK CLARKE 变换 变换 电流磁链 异步 位置转换 电动机 编码器 图1闭环矢量控制系统 Fig.1 Closed-loop vector control system 1.2离线整定 加适当的PI调节器加以校正，将内环（磁通环和转 为了获得更加优良的控制效果，采用改进的基 矩环)校正为典型1型系统，提高控制系统的动态响 于模型的整定方法.在实际电机控制系统中，通常都 应性能，将外环（转速环）校正为典型Ⅱ型系统，提 采用PI控制.由图1可知，整个控制系统是一个双 高系统的抗干扰能力.PI调节器设计的一般原则为 闭环调速系统，转矩环和磁通环属于内环，速度环为 从内环到外环2) 外环.未加PI调节器的内环和外环的开环传递函数 1.2.1磁通环PI计算 构成的系统都不是典型系统，难以稳定运行，需要添 要保持电机稳定运行，则必须使磁通在恒转矩

参数自整定主要分为基于规则的自整定[１０￣１１] 、基于 模型的自整定和智能 ＰＩＤ 参数自整定[１￣２] . 为了使系统工作在最佳状态下ꎬ本文采用离线 整定与在线整定相结合的方式ꎬ首先构建较为精确 的异步电机矢量控制数学模型ꎬ在系统运行前计算 出系统最优 ＰＩ 参数ꎬ然后启动系统ꎬ采用模糊 ＰＩ 控 制器进行在线实时整定ꎬ极大地提高了系统的动态 性能. １ ＰＩＤ 参数混合整定法 １.１ 闭环矢量控制系统及整定算法 异步电机的数学模型是高阶、非线性、强耦合的 多变量系统ꎬ采用矢量控制可以实现异步电机的高 性能控制ꎬ本文所采用的闭环矢量控制系统如图 １ 所示.由于异步交流电机本身精度较差ꎬ要获取较高 的控制精度ꎬ就需要获取最优的 ＰＩＤ 参数ꎬ使整个 控制系统工作在最佳状态.目前大多数调速系统都 只采用某一种整定方式(离线整定或在线实时整 定)ꎬ如有的系统采用继电振荡法计算出 ＰＩＤ 参数 后ꎬ在电机运行过程中便不再改变参数ꎬ这是离线式 整定ꎻ有的系统则采用智能整定法对系统进行实时 ＰＩＤ 参数修正ꎬ这是在线实时整定.单一的整定方式 都有其局限性ꎬ如果只采用离线整定ꎬ系统运行过程 中通常环境或系统本身会发生变化(如外部干扰或 因电机长时间运行导致电机自身电阻、电感等参数 发生变化等)ꎬ仅采用系统运行前整定的参数难以 适应这些变化ꎬ导致控制系统性能下降甚至无法稳 定运行ꎻ如果只采用在线实时整定ꎬ通常系统启动时 的参数都未经整定ꎬ若参数选择不合适ꎬ会导致实时 在线整定时间过长甚至无法正常启动ꎬ对于一些精 密系统ꎬ启动时的较大波动容易引起设备损坏.因 此ꎬ最佳的整定方法应为离线与在线整定相结合的 方式ꎬ首先根据系统运行之前的状态整定出较好的 ＰＩＤ 参数ꎬ保证系统正常启动ꎬ并使系统平滑过渡到 在线整定状态ꎻ在运行过程中ꎬ在线整定可使系统能 根据环境或系统自身的变化而自动修正 ＰＩＤ 参数ꎬ 让系统始终运行在最佳状态. 图 １ 闭环矢量控制系统 Ｆｉｇ.１ Ｃｌｏｓｅｄ￣ｌｏｏｐ ｖｅｃｔｏｒ ｃｏｎｔｒｏｌ ｓｙｓｔｅｍ １.２ 离线整定 为了获得更加优良的控制效果ꎬ采用改进的基 于模型的整定方法.在实际电机控制系统中ꎬ通常都 采用 ＰＩ 控制.由图 １ 可知ꎬ整个控制系统是一个双 闭环调速系统ꎬ转矩环和磁通环属于内环ꎬ速度环为 外环.未加 ＰＩ 调节器的内环和外环的开环传递函数 构成的系统都不是典型系统ꎬ难以稳定运行ꎬ需要添 加适当的 ＰＩ 调节器加以校正ꎬ将内环(磁通环和转 矩环)校正为典型 Ｉ 型系统ꎬ提高控制系统的动态响 应性能ꎬ将外环(转速环)校正为典型 ＩＩ 型系统ꎬ提 高系统的抗干扰能力.ＰＩ 调节器设计的一般原则为 从内环到外环[１２￣１３] . １.２.１ 磁通环 ＰＩ 计算 要保持电机稳定运行ꎬ则必须使磁通在恒转矩 第 ５ 期 李鹏ꎬ等:ＰＩ 参数混合整定法在闭环矢量控制系统中的应用 􀅰４４７􀅰

·448 智能系统学报 第8卷 时保持恒定，在负载变化较大时，使其有较好的跟随 快，有的则需要稳态精度高，因此这里可根据实际情 性能.磁通环的闭环结构如图2所示. 况选择阻尼比.因此，可计算得PI参数为： 磁通环 R PI调节器 fait. K,= 4BoT,T.L Ki= 图2磁通环结构 T Fig.2 Construction of flux loops 在输出端，需对V加入磁通环补偿6ω，i(L,- 易推得磁通环的传递函数为一般典型二阶系统： 乎(s) L/R 冬“方台系流酒安信视下取=1，两相装我 G()=)T,Ts+(T,+T,)s+1 场需求适当调大， 式中： 1.2.2转矩环PI计算 ,T=5,0=1 转矩与定子电流9轴分量成线性关系，因此转 T,= 矩环实际上是电流内环，由q轴电压输出分量与反 G(s)为一个二阶系统，需要引入1个PI调节器 馈电流的关系可推出其闭环结构如图3所示 增加一个零极点以校正为典型I型系统.图2中 转矩环 PI调节器 ,(化，元)为据合项，为了去除耦合影响，需在输 YodLint rLis L. Ts+l 出端进行补偿，因此在设计PI调节器时不考虑该 图3转矩环结构 项，设PI调节器的传递函数为 K()=K(s+1) Fig.3 Construction of torque loops 反馈电流，由于滤波环节的存在，因此有延迟， TS 故为了消除延迟环节的影响，在前向通道加入1个惯 式中：K。为比例系数，T为积分时间参数.磁通环校 正后的传递函数为 性环节为滤波时间常数。由系统硬件支款件 M(s)=G(s)K(s)= 滤波器决定.由图3也可知，电压含有转差率的耦合 KL (Ts 1)/R, 项，因此需在输出端进行补偿，而在设计调节器的时 Ts(OT,Ts2+(T.+T)s+1) 候可将其忽略.转矩环的等效开环传递函数为 K L(Ts 1)/R, TSOT,T,(As 1)(Bs +1) 式中： G)=(R,+l,)(T+D 加入PI调节器后的传递函数为 20T.T A= M(s)=G(s)K(s)= (T,+T,)+√(T+T)2-4oTT K,(Ts+1)/R 20TT B=- (T,+T,)-(T,+T,)2-4oTT, (R+1)(+) 根据零极点相消原理，应该将T取值为A、B中 通常滤波时间常数都很小，因此可视为σL/R,> 较小的那个值以消去一个偏离零轴较远的极点，提 T,上式中M(s)需消去较大的极点，即消去分母中 高系统响应速度，故T=A. (Ts+1)项，此时r=T 因此 与磁通环计算方法相同，有 K BLn/R M(s)= K。= K= saT,T,(Bs 1) 45L, T 易知该I型系统的阻尼比为 转矩环的闭环传递函数为 1 1 5a= G,(s)= 2VK B'oT T L/R 43 4σL, 2s+1 通常情况下选择阻尼比：=0.707，但在不同生 R 5+ R 产流水线上要求会有不同，有的系统要求响应时间 在输出端，需对V加入磁通环补偿-Bω，(L,ia+

时保持恒定ꎬ在负载变化较大时ꎬ使其有较好的跟随 性能.磁通环的闭环结构如图 ２ 所示. 图 ２ 磁通环结构 Ｆｉｇ.２ Ｃｏｎｓｔｒｕｃｔｉｏｎ ｏｆ ｆｌｕｘ ｌｏｏｐｓ 易推得磁通环的传递函数为一般典型二阶系统: Ｇ(ｓ) ＝ Ψｒｄ(ｓ) Ｖｓｄ(ｓ) ＝ Ｌｍ / Ｒｓ σＴｓＴｒ ｓ ２ ＋ (Ｔｓ ＋ Ｔｒ)ｓ ＋ １ . 式中: Ｔｒ ＝ Ｌｒ Ｒｒ ꎬＴｓ ＝ Ｌｓ Ｒｓ ꎬσ ＝ １ － Ｌ ２ ｍ ＬｓＬｒ . Ｇ(ｓ)为一个二阶系统ꎬ需要引入 １ 个 ＰＩ 调节器 增加一个零极点以校正为典型 Ｉ 型系统. 图 ２ 中 ωｓ ｉ ｓｑ(Ｌｓ － Ｌ ２ ｍｒ Ｌｒ )为耦合项ꎬ为了去除耦合影响ꎬ需在输 出端进行补偿ꎬ因此在设计 ＰＩ 调节器时不考虑该 项ꎬ设 ＰＩ 调节器的传递函数为 Ｋ(ｓ) ＝ Ｋｐ(τｓ ＋ １) τｓ . 式中:Ｋｐ 为比例系数ꎬτ 为积分时间参数.磁通环校 正后的传递函数为 Ｍ(ｓ) ＝ Ｇ(ｓ)Ｋ(ｓ) ＝ Ｋｐ Ｌｍ(τｓ ＋ １) / Ｒｓ τｓ(σＴｓＴｒ ｓ ２ ＋ (Ｔｓ ＋ Ｔｒ)ｓ ＋ １) ＝ Ｋｐ Ｌｍ(τｓ ＋ １) / Ｒｓ τｓσＴｓＴｒ(Ａｓ ＋ １)(Ｂｓ ＋ １) . 式中: Ａ ＝ ２σＴｓＴ (Ｔｓ ＋ Ｔｒ) ＋ (Ｔｓ ＋ Ｔｒ) ２ － ４σＴｓＴｒ ꎬ Ｂ ＝ ２σＴｓＴ (Ｔｓ ＋ Ｔｒ) － (Ｔｓ ＋ Ｔｒ) ２ － ４σＴｓＴｒ . 根据零极点相消原理ꎬ应该将 τ 取值为 Ａ、Ｂ 中 较小的那个值以消去一个偏离零轴较远的极点ꎬ提 高系统响应速度ꎬ故 τ ＝ Ａ. 因此 Ｍ(ｓ) ＝ ＫｐＢＬｍ / Ｒｓ ｓσＴｓＴｒ(Ｂｓ ＋ １) . 易知该 Ｉ 型系统的阻尼比为 ζｄ ＝ １ ２ ＫｐＢ ２σＴｓＴｒＬｍ / Ｒｓ . 通常情况下选择阻尼比 ζ ＝ ０.７０７ꎬ但在不同生 产流水线上要求会有不同ꎬ有的系统要求响应时间 快ꎬ有的则需要稳态精度高ꎬ因此这里可根据实际情 况选择阻尼比.因此ꎬ可计算得 ＰＩ 参数为: Ｋｐ ＝ Ｒｓ ４ζ ２ ｄＢ ２σＴｓＴｒＬｍ ꎬ Ｋｉ ＝ Ｋｐ τ . 在输出端ꎬ需对 Ｖｓｄ加入磁通环补偿 εωｓ ｉ ｓｑ( Ｌｓ － Ｌ ２ ｍｒ Ｌｒ )ꎬε 为补偿系数ꎬ通常情况下取 ε ＝ １ꎬ可根据现 场需求适当调大. １.２.２ 转矩环 ＰＩ 计算 转矩与定子电流 ｑ 轴分量成线性关系ꎬ因此转 矩环实际上是电流内环ꎬ由 ｑ 轴电压输出分量与反 馈电流的关系可推出其闭环结构如图 ３ 所示. 图 ３ 转矩环结构 Ｆｉｇ.３ Ｃｏｎｓｔｒｕｃｔｉｏｎ ｏｆ ｔｏｒｑｕｅ ｌｏｏｐｓ 反馈电流 ｉ ｓｑ由于滤波环节的存在ꎬ因此有延迟ꎬ 故为了消除延迟环节的影响ꎬ在前向通道加入 １ 个惯 性环节 １ Ｔｆ ｓ＋１ ꎬＴｆ 为滤波时间常数ꎬ由系统硬件或软件 滤波器决定.由图 ３ 也可知ꎬ电压含有转差率的耦合 项ꎬ因此需在输出端进行补偿ꎬ而在设计调节器的时 候可将其忽略.转矩环的等效开环传递函数为 Ｇ(ｓ) ＝ １ (Ｒｓ ＋ σＬｓ ｓ)(Ｔｆ ｓ ＋ １) . 加入 ＰＩ 调节器后的传递函数为 Ｍ(ｓ) ＝ Ｇ(ｓ)Ｋ(ｓ) ＝ Ｋｐ(τｓ ＋ １) / Ｒｓ τｓ( σＬｓ Ｒｓ ｓ ＋ １)(Ｔｆ ｓ ＋ １) . 通常滤波时间常数都很小ꎬ因此可视为σＬｓ / Ｒｓ> Ｔｆꎬ上式中 Ｍ(ｓ)需消去较大的极点ꎬ即消去分母中 (Ｔｆ ｓ＋１)项ꎬ此时 τ ＝ Ｔｆ . 与磁通环计算方法相同ꎬ有 Ｋｐ ＝ Ｒ ２ ｓ Ｔｆ ４ζ ２ ｑσＬｓ ꎬＫｉ ＝ Ｋｐ Ｔｆ . 转矩环的闭环传递函数为 Ｇｑ(ｓ) ＝ １ ４σ ２ Ｌ ２ ｓ ζ ２ ｑ Ｒ ２ ｓ ｓ ２ ＋ ４σＬｓ ζ ２ ｑ Ｒｓ ｓ ＋ １ . 在输出端ꎬ 需对 Ｖｓｄ 加入磁通环补偿 － βωｓ ( Ｌｓ ｉ ｓｄ ＋ 􀅰４４８􀅰 智 能 系 统 学 报 第 ８ 卷

第5期 李鹏，等：PI参数混合整定法在闭环矢量控制系统中的应用 449· Y。-L),s为补偿系数，通常情况下取B=1, 然后立刻关掉转矩给定，让电机靠摩擦力自由停机， L L 此时的负载转矩即为摩擦转矩T。·记录转速从ω降 适当增大可减小速度脉动. 为0所用的时间ta,有 1.2.3转速环PI计算 、 =0-T (4) 从异步电机输出转矩到转速可以视为一个积分 nta 环节.在调速系统中，转速给定的急剧变化容易引起 由式(3)和(4)可解得 电机系统的不稳定，因此常将其配置成典型Ⅱ型系 J=nTtta 统由于速度检测有滞后环节，因此需在速度给定的 (t,+ta) 前向通道上增加一个惯性环节，同时考虑转矩环的 上述3个调节器都是近似计算所得，因此整定 等效闭环传递函数，转速环的结构如图4所示 出的参数通常只是接近最优参数，在实际调试时需 要在整定参数附近根据需要加以调整。 1.3在线实时整定 转速环 1△7 s+ PI调节器 当离线整定完毕后，系统3个PI控制器会计算 出各自的PI参数，但在系统启动之后，随着运行环 T3+1 境和条件的改变，PI参数也需要作出相应调整，以 图4转速环结构 保证系统处于最佳运行状态.系统的内环相对稳定， Fig.4 Construction of speed loops 但外环对外界扰动响应较快，因此需要对外环即速 容易知道转速环的开环传递函数（包含PI调节 度环进行在线的PI参数实时调整，并且要求调整时 器)为 PI参数计算必须在极短时间内完成，以免影响整定 G(s)= 的实时性 K(Ts +1) 模糊控制方法目前被视为高性能电机控制系统 +oL≤+1)T+) 的良好解决方案，能够对脉冲式负载冲击扰动作出 JTs(- R2 R. 快速响应，增加驱动系统惯量的鲁棒性，且其计算量 式中：J为电机的转动惯量.略去上式分母中高次项， 小、实时性强，因此选择模糊PI控制器来进行在线 合并小惯性环节，可得转速环开环传递函数近似为 实时PI参数整定. K(Ts+1) 模糊PI控制器在整个系统中的位置和结构如 G(s)= s2(Tms 1) 图1所示，其输入端的e.为误差的变化率.它只在离 式中： 线整定完毕后系统运行过程中启动，实时调整速度 环的PI参数. T.m=T+R. (1) 在模糊控制系统中，需先对输入量进行模糊化， 设H=r/T,表示中频段带宽，由最小M,设计法 而模糊化中的隶属度函数至关重要，其对整个控制 可得4 系统的稳定性和快速性有着很大影响.一般采用高 斯型隶属度函数性能较好，但其计算量较大，在实时 H+1 K= 2 2HTm 性要求高的地方通常选择性能与高斯函数较为接近 由式(1)和(2)可得 但计算量小很多的三角函数，如图5所示.输入e、e. J(H+1) 和输出K。、K,的论域可根据实际需求修改。 K=2HT.m NM NS PM PB 式中：H的取值范围通常为5~11 1.2.4转动惯量的计算 0.5 转动惯量采用加减速法测定，首先让异步电机 以恒转矩从零速启动（如有负载亦可将其视为一个 整体)，当电机角速度达到ω时，记录电机速度上升 输入输出 运行时间(，根据电机与转动惯量的关系有 图5输入输出的隶属度函数 Fig.5 Membership function of input and output =T。-To (3) nt

Ｌｍ Ψｒｄ －Ｌｍ ｉ ｓｄ Ｌｒ )ꎬε 为补偿系数ꎬ通常情况下取 β ＝ １ꎬ 适当增大可减小速度脉动. １.２.３ 转速环 ＰＩ 计算 从异步电机输出转矩到转速可以视为一个积分 环节.在调速系统中ꎬ转速给定的急剧变化容易引起 电机系统的不稳定ꎬ因此常将其配置成典型 ＩＩ 型系 统.由于速度检测有滞后环节ꎬ因此需在速度给定的 前向通道上增加一个惯性环节ꎬ同时考虑转矩环的 等效闭环传递函数ꎬ转速环的结构如图 ４ 所示. 图 ４ 转速环结构 Ｆｉｇ.４ Ｃｏｎｓｔｒｕｃｔｉｏｎ ｏｆ ｓｐｅｅｄ ｌｏｏｐｓ 容易知道转速环的开环传递函数(包含 ＰＩ 调节 器)为 Ｇ(ｓ) ＝ Ｋｐ(τｓ ＋ １) Ｊτｓ ２ ( ４σ ２ Ｌ ２ ｓ ζ ２ ｑ Ｒ ２ ｓ ｓ ２ ＋ ４σＬｓ ζ ２ ｑ Ｒｓ ｓ ＋ １)(Ｔｆ ｓ ＋ １) . 式中:Ｊ 为电机的转动惯量.略去上式分母中高次项ꎬ 合并小惯性环节ꎬ可得转速环开环传递函数近似为 Ｇ(ｓ) ＝ Ｋ(τｓ ＋ １) ｓ ２ (Ｔｓｕｍ ｓ ＋ １) . 式中: Ｔｓｕｍ ＝ Ｔｆ ＋ ４σＬｓ ζ ２ ｑ Ｒｓ ꎬＫ ＝ Ｋｐ Ｊτ . (１) 设 Ｈ＝ τ / Ｔｆ 表示中频段带宽ꎬ由最小 Ｍｒ 设计法 可得[１４] Ｋ ＝ Ｈ ＋ １ ２Ｈ ２ Ｔ ２ ｓｕｍ . (２) 由式(１)和(２)可得 Ｋｐ ＝ Ｊ(Ｈ ＋ １) ２ＨＴｓｕｍ . 式中:Ｈ 的取值范围通常为 ５~１１. １.２.４ 转动惯量的计算 转动惯量采用加减速法测定ꎬ首先让异步电机 以恒转矩从零速启动(如有负载亦可将其视为一个 整体)ꎬ当电机角速度达到 ω 时ꎬ记录电机速度上升 运行时间 ｔ ｒꎬ根据电机与转动惯量的关系有 Ｊω ｎｐ ｔ ｒ ＝ Ｔｅ － Ｔ０ . (３) 然后立刻关掉转矩给定ꎬ让电机靠摩擦力自由停机ꎬ 此时的负载转矩即为摩擦转矩 Ｔ０ .记录转速从 ω 降 为 ０ 所用的时间 ｔ ｄ ꎬ有 － Ｊω ｎｐ ｔ ｄ ＝ ０ － Ｔ０ . (４) 由式(３)和(４)可解得 Ｊ ＝ ｎｐＴｅ ｔ ｒ ｔ ｄ ω(ｔ ｒ ＋ ｔ ｄ ) . 上述 ３ 个调节器都是近似计算所得ꎬ因此整定 出的参数通常只是接近最优参数ꎬ在实际调试时需 要在整定参数附近根据需要加以调整. １.３ 在线实时整定 当离线整定完毕后ꎬ系统 ３ 个 ＰＩ 控制器会计算 出各自的 ＰＩ 参数ꎬ但在系统启动之后ꎬ随着运行环 境和条件的改变ꎬＰＩ 参数也需要作出相应调整ꎬ以 保证系统处于最佳运行状态.系统的内环相对稳定ꎬ 但外环对外界扰动响应较快ꎬ因此需要对外环即速 度环进行在线的 ＰＩ 参数实时调整ꎬ并且要求调整时 ＰＩ 参数计算必须在极短时间内完成ꎬ以免影响整定 的实时性. 模糊控制方法目前被视为高性能电机控制系统 的良好解决方案ꎬ能够对脉冲式负载冲击扰动作出 快速响应ꎬ增加驱动系统惯量的鲁棒性ꎬ且其计算量 小、实时性强ꎬ因此选择模糊 ＰＩ 控制器来进行在线 实时 ＰＩ 参数整定. 模糊 ＰＩ 控制器在整个系统中的位置和结构如 图 １ 所示ꎬ其输入端的 ｅｃ 为误差的变化率.它只在离 线整定完毕后系统运行过程中启动ꎬ实时调整速度 环的 ＰＩ 参数. 在模糊控制系统中ꎬ需先对输入量进行模糊化ꎬ 而模糊化中的隶属度函数至关重要ꎬ其对整个控制 系统的稳定性和快速性有着很大影响.一般采用高 斯型隶属度函数性能较好ꎬ但其计算量较大ꎬ在实时 性要求高的地方通常选择性能与高斯函数较为接近 但计算量小很多的三角函数ꎬ如图 ５ 所示.输入 ｅ、ｅｃ 和输出 Ｋｐ 、Ｋｉ 的论域可根据实际需求修改. 图 ５ 输入输出的隶属度函数 Ｆｉｇ.５ Ｍｅｍｂｅｒｓｈｉｐ ｆｕｎｃｔｉｏｎ ｏｆ ｉｎｐｕｔ ａｎｄ ｏｕｔｐｕｔ 第 ５ 期 李鹏ꎬ等:ＰＩ 参数混合整定法在闭环矢量控制系统中的应用 􀅰４４９􀅰

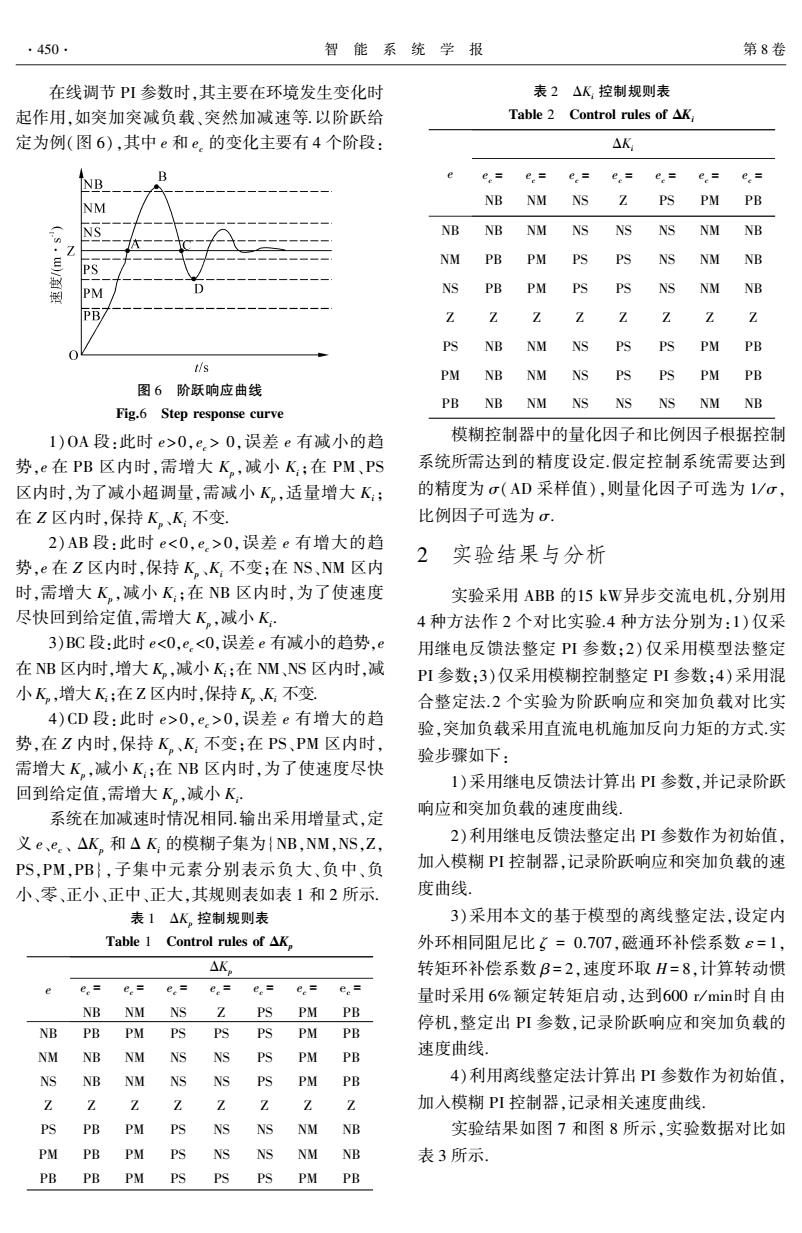
·450· 智能系统学报 第8卷 在线调节PI参数时，其主要在环境发生变化时 表2△K控制规则表 起作用，如突加突减负载、突然加减速等以阶跃给 Table 2 Control rules of AK, 定为例（图6），其中e和e.的变化主要有4个阶段： △K NB e e.= e= e。=e,=e.= e= NM NB NM NS 2 PS PM PB NS NB NB NM NS NS NS NM NB NM PB PM PS PS NS NM NB PS PM D NS PB PM Ns NM NB PBA Z Z Z Z Z Z PS NB PS PS PM PB t/s PM NB NM NS PS PS PM PB 图6阶跃响应曲线 PB NB NM NS NS NS NM NB Fig.6 Step response curve 1)0A段：此时e>0,e,>0,误差e有减小的趋 模糊控制器中的量化因子和比例因子根据控制 势，e在PB区内时，需增大K,减小K;在PM、PS 系统所需达到的精度设定假定控制系统需要达到 区内时，为了减小超调量，需减小K,适量增大K: 的精度为σ(AD采样值)，则量化因子可选为1/σ， 在Z区内时，保持K。K不变 比例因子可选为σ 2)AB段：此时e0,误差e有增大的趋 2实验结果与分析 势，e在Z区内时，保持K。、K,不变；在NS、NM区内 时，需增大K,减小K;在NB区内时，为了使速度 实验采用ABB的15kW异步交流电机，分别用 尽快回到给定值，需增大K,减小K 4种方法作2个对比实验.4种方法分别为：1)仅采 3)BC段：此时e0,e.>0,误差e有增大的趋 验，突加负载采用直流电机施加反向力矩的方式实 势，在Z内时，保持K。、K,不变；在PS、PM区内时， 验步骤如下： 需增大K。,减小K;在NB区内时，为了使速度尽快 1)采用继电反馈法计算出PI参数，并记录阶跃 回到给定值，需增大K。,减小K 系统在加减速时情况相同.输出采用增量式，定 响应和突加负载的速度曲线. 义e、e、△K,和△K的模糊子集为{NB,NM,NS,Z, 2)利用继电反馈法整定出PI参数作为初始值， PS,PM,PB},子集中元素分别表示负大、负中、负 加入模糊PI控制器，记录阶跃响应和突加负载的速 小、零、正小、正中、正大，其规则表如表1和2所示. 度曲线 表1△K,控制规则表 3)采用本文的基于模型的离线整定法，设定内 Table 1 Control rules of AK, 外环相同阻尼比(=0.707，磁通环补偿系数ε=1， △K 转矩环补偿系数B=2,速度环取H=8,计算转动惯 e。 e.=e= e.=e,=e=e.= 量时采用6%额定转矩启动，达到600r/min时自由 NB NM NS Z PS PM PB nB PB PM PSPS PS PM PB 停机，整定出PI参数，记录阶跃响应和突加负载的 NM NB NM NS NS PS PM PB 速度曲线。 NS NB NM NS NS PS PM PB 4)利用离线整定法计算出PI参数作为初始值， Z Z 1 加入模糊PI控制器，记录相关速度曲线。 PS PB PM PS NS NS NM NB 实验结果如图7和图8所示，实验数据对比如 PM PB PM PS NS NS NM NB 表3所示. PBPB PM PS PSPS PM PB

在线调节 ＰＩ 参数时ꎬ其主要在环境发生变化时 起作用ꎬ如突加突减负载、突然加减速等.以阶跃给 定为例(图 ６)ꎬ其中 ｅ 和 ｅｃ 的变化主要有 ４ 个阶段: 图 ６ 阶跃响应曲线 Ｆｉｇ.６ Ｓｔｅｐ ｒｅｓｐｏｎｓｅ ｃｕｒｖｅ １)ＯＡ 段:此时 ｅ>０ꎬｅｃ > ０ꎬ误差 ｅ 有减小的趋 势ꎬｅ 在 ＰＢ 区内时ꎬ需增大 Ｋｐꎬ减小 Ｋｉꎻ在 ＰＭ、ＰＳ 区内时ꎬ为了减小超调量ꎬ需减小 Ｋｐꎬ适量增大 Ｋｉꎻ 在 Ｚ 区内时ꎬ保持 Ｋｐ、Ｋｉ 不变. ２)ＡＢ 段:此时 ｅ ０ꎬ误差 ｅ 有增大的趋 势ꎬｅ 在 Ｚ 区内时ꎬ保持 Ｋｐ、Ｋｉ 不变ꎻ在 ＮＳ、ＮＭ 区内 时ꎬ需增大 Ｋｐꎬ减小 Ｋｉꎻ在 ＮＢ 区内时ꎬ为了使速度 尽快回到给定值ꎬ需增大 Ｋｐꎬ减小 Ｋｉ . ３)ＢＣ 段:此时 ｅ ０ꎬｅｃ > ０ꎬ误差 ｅ 有增大的趋 势ꎬ在 Ｚ 内时ꎬ保持 Ｋｐ、Ｋｉ 不变ꎻ在 ＰＳ、ＰＭ 区内时ꎬ 需增大 Ｋｐꎬ减小 Ｋｉꎻ在 ＮＢ 区内时ꎬ为了使速度尽快 回到给定值ꎬ需增大 Ｋｐꎬ减小 Ｋｉ . 系统在加减速时情况相同.输出采用增量式ꎬ定 义 ｅ、ｅｃ、 ΔＫｐ 和 Δ Ｋｉ 的模糊子集为{ＮＢꎬＮＭꎬＮＳꎬＺꎬ ＰＳꎬＰＭꎬＰＢ}ꎬ子集中元素分别表示负大、负中、负 小、零、正小、正中、正大ꎬ其规则表如表 １ 和 ２ 所示. 表 １ ΔＫｐ 控制规则表 Ｔａｂｌｅ １ Ｃｏｎｔｒｏｌ ｒｕｌｅｓ ｏｆ ΔＫｐ ｅ ΔＫｐ ｅｃ ＝ ＮＢ ｅｃ ＝ ＮＭ ｅｃ ＝ ＮＳ ｅｃ ＝ Ｚ ｅｃ ＝ ＰＳ ｅｃ ＝ ＰＭ ｅｃ ＝ ＰＢ ＮＢ ＰＢ ＰＭ ＰＳ ＰＳ ＰＳ ＰＭ ＰＢ ＮＭ ＮＢ ＮＭ ＮＳ ＮＳ ＰＳ ＰＭ ＰＢ ＮＳ ＮＢ ＮＭ ＮＳ ＮＳ ＰＳ ＰＭ ＰＢ Ｚ Ｚ Ｚ Ｚ Ｚ Ｚ Ｚ Ｚ ＰＳ ＰＢ ＰＭ ＰＳ ＮＳ ＮＳ ＮＭ ＮＢ ＰＭ ＰＢ ＰＭ ＰＳ ＮＳ ＮＳ ＮＭ ＮＢ ＰＢ ＰＢ ＰＭ ＰＳ ＰＳ ＰＳ ＰＭ ＰＢ 表 ２ ΔＫｉ 控制规则表 Ｔａｂｌｅ ２ Ｃｏｎｔｒｏｌ ｒｕｌｅｓ ｏｆ ΔＫｉ ｅ ΔＫｉ ｅｃ ＝ ＮＢ ｅｃ ＝ ＮＭ ｅｃ ＝ ＮＳ ｅｃ ＝ Ｚ ｅｃ ＝ ＰＳ ｅｃ ＝ ＰＭ ｅｃ ＝ ＰＢ ＮＢ ＮＢ ＮＭ ＮＳ ＮＳ ＮＳ ＮＭ ＮＢ ＮＭ ＰＢ ＰＭ ＰＳ ＰＳ ＮＳ ＮＭ ＮＢ ＮＳ ＰＢ ＰＭ ＰＳ ＰＳ ＮＳ ＮＭ ＮＢ Ｚ Ｚ Ｚ Ｚ Ｚ Ｚ Ｚ Ｚ ＰＳ ＮＢ ＮＭ ＮＳ ＰＳ ＰＳ ＰＭ ＰＢ ＰＭ ＮＢ ＮＭ ＮＳ ＰＳ ＰＳ ＰＭ ＰＢ ＰＢ ＮＢ ＮＭ ＮＳ ＮＳ ＮＳ ＮＭ ＮＢ 模糊控制器中的量化因子和比例因子根据控制 系统所需达到的精度设定.假定控制系统需要达到 的精度为 σ(ＡＤ 采样值)ꎬ则量化因子可选为 １ / σꎬ 比例因子可选为 σ. ２ 实验结果与分析 实验采用 ＡＢＢ 的１５ ｋＷ异步交流电机ꎬ分别用 ４ 种方法作 ２ 个对比实验.４ 种方法分别为:１)仅采 用继电反馈法整定 ＰＩ 参数ꎻ２) 仅采用模型法整定 ＰＩ 参数ꎻ３)仅采用模糊控制整定 ＰＩ 参数ꎻ４)采用混 合整定法.２ 个实验为阶跃响应和突加负载对比实 验ꎬ突加负载采用直流电机施加反向力矩的方式.实 验步骤如下: １)采用继电反馈法计算出 ＰＩ 参数ꎬ并记录阶跃 响应和突加负载的速度曲线. ２)利用继电反馈法整定出 ＰＩ 参数作为初始值ꎬ 加入模糊 ＰＩ 控制器ꎬ记录阶跃响应和突加负载的速 度曲线. ３)采用本文的基于模型的离线整定法ꎬ设定内 外环相同阻尼比 ζ ＝ ０.７０７ꎬ磁通环补偿系数 ε ＝ １ꎬ 转矩环补偿系数 β ＝ ２ꎬ速度环取 Ｈ ＝ ８ꎬ计算转动惯 量时采用 ６％额定转矩启动ꎬ达到６００ ｒ/ ｍｉｎ时自由 停机ꎬ整定出 ＰＩ 参数ꎬ记录阶跃响应和突加负载的 速度曲线. ４)利用离线整定法计算出 ＰＩ 参数作为初始值ꎬ 加入模糊 ＰＩ 控制器ꎬ记录相关速度曲线. 实验结果如图 ７ 和图 ８ 所示ꎬ实验数据对比如 表 ３ 所示. 􀅰４５０􀅰 智 能 系 统 学 报 第 ８ 卷

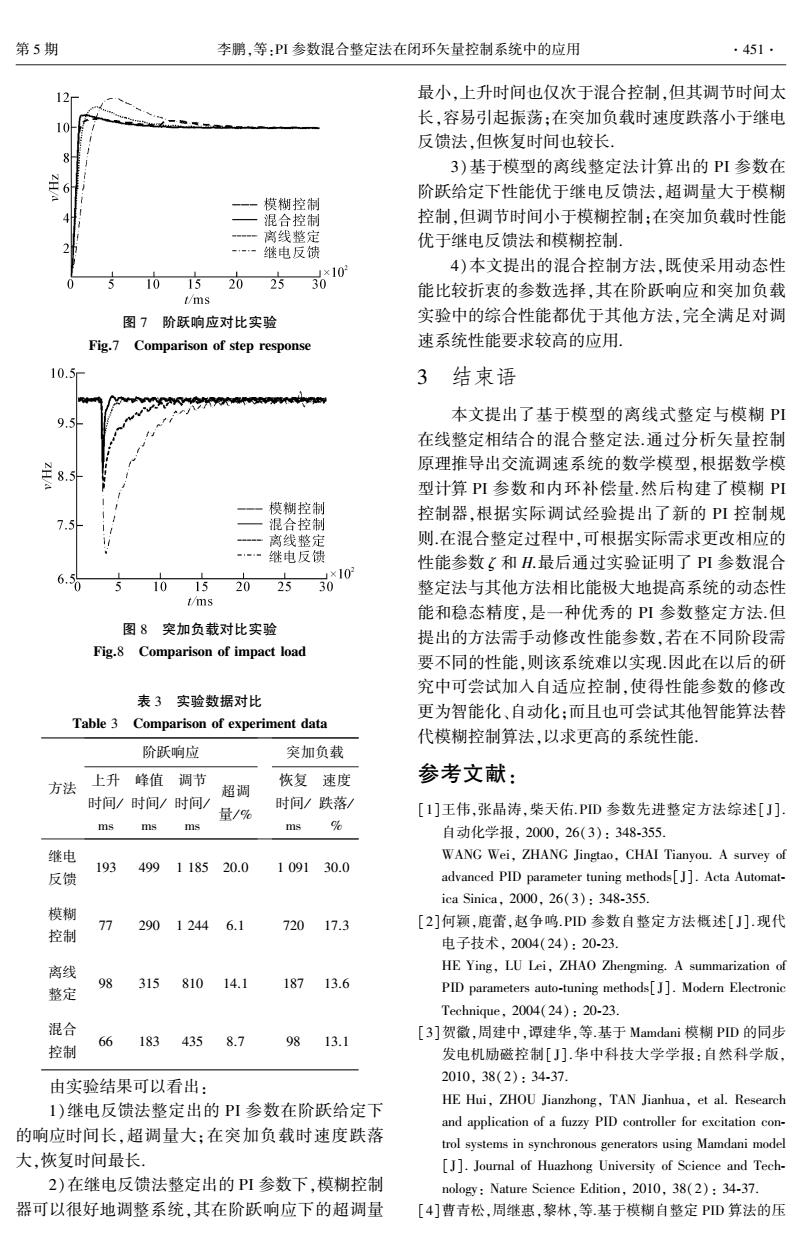
第5期 李鹏，等：PI参数混合整定法在闭环矢量控制系统中的应用 ·451· 12 最小，上升时间也仅次于混合控制，但其调节时间太 长，容易引起振荡：在突加负载时速度跌落小于继电 10 反馈法，但恢复时间也较长， 3)基于模型的离线整定法计算出的PI参数在 阶跃给定下性能优于继电反馈法，超调量大于模糊 模糊控制 混合控制 控制，但调节时间小于模糊控制：在突加负载时性能 离线整定 优于继电反馈法和模糊控制. 继电反馈 ×10 4)本文提出的混合控制方法，既使采用动态性 15 2025 30 能比较折衷的参数选择，其在阶跃响应和突加负载 t/ms 图7阶跃响应对比实哈 实验中的综合性能都优于其他方法，完全满足对调 Fig.7 Comparison of step response 速系统性能要求较高的应用. 10. 3结束语 本文提出了基于模型的离线式整定与模糊PI 在线整定相结合的混合整定法.通过分析矢量控制 原理推导出交流调速系统的数学模型，根据数学模 型计算PI参数和内环补偿量.然后构建了模糊PI 模糊控制 控制器，根据实际调试经验提出了新的PI控制规 混合控制 一离线整定 则.在混合整定过程中，可根据实际需求更改相应的 继电反馈 性能参数（和H.最后通过实验证明了PI参数混合 ×10 1015 20 25 30 整定法与其他方法相比能极大地提高系统的动态性 t/ms 能和稳态精度，是一种优秀的PI参数整定方法.但 图8突加负载对比实验 提出的方法需手动修改性能参数，若在不同阶段需 Fig.8 Comparison of impact load 要不同的性能，则该系统难以实现.因此在以后的研 究中可尝试加入自适应控制，使得性能参数的修改 表3实验数据对比 更为智能化、自动化：而且也可尝试其他智能算法替 Table 3 Comparison of experiment data 代模糊控制算法，以求更高的系统性能。 阶跃响应 突加负载 参考文献： 方法 上升峰值调节 恢复速度 超调 时间/时间/时间/ 时间/跌落/ 量/% [1]王伟，张晶涛，柴天佑.PD参数先进整定方法综述[J]. ms ms ms ms % 自动化学报，2000,26(3)：348-355. 继电 WANG Wei,ZHANG Jingtao,CHAI Tianyou.A survey of 193 499 1185 20.0 1091 30.0 反馈 advanced PID parameter tuning methods[J].Acta Automat- ica Sinica,2000,26(3):348-355. 模糊 77 29012446.1 720 17.3 [2]何颖，鹿蕾，赵争鸣.PD参数自整定方法概述[J].现代 控制 电子技术，2004(24)：20-23. 离线 HE Ying,LU Lei,ZHAO Zhengming.A summarization of 98 315 810 14.1 187 13.6 整定 PID parameters auto-tuning methods[J].Modern Electronic Technique,2004(24):20-23. 混合 66 183 435 8.7 98 13.1 [3]贺徽，周建中，谭建华，等.基于Mamdani模糊PD的同步 控制 发电机励磁控制[J].华中科技大学学报：自然科学版， 由实验结果可以看出： 2010,38(2):34-37. HE Hui,ZHOU Jianzhong,TAN Jianhua,et al.Research 1)继电反馈法整定出的PI参数在阶跃给定下 and application of a fuzzy PID controller for excitation con- 的响应时间长，超调量大：在突加负载时速度跌落 trol systems in synchronous generators using Mamdani model 大，恢复时间最长。 [J].Journal of Huazhong University of Science and Tech- 2)在继电反馈法整定出的PI参数下，模糊控制 nology:Nature Science Edition,2010,38(2):34-37. 器可以很好地调整系统，其在阶跃响应下的超调量 [4]曹青松，周继惠，黎林，等.基于模糊自整定PD算法的压

图 ７ 阶跃响应对比实验 Ｆｉｇ.７ Ｃｏｍｐａｒｉｓｏｎ ｏｆ ｓｔｅｐ ｒｅｓｐｏｎｓｅ 图 ８ 突加负载对比实验 Ｆｉｇ.８ Ｃｏｍｐａｒｉｓｏｎ ｏｆ ｉｍｐａｃｔ ｌｏａｄ 表 ３ 实验数据对比 Ｔａｂｌｅ ３ Ｃｏｍｐａｒｉｓｏｎ ｏｆ ｅｘｐｅｒｉｍｅｎｔ ｄａｔａ 方法 阶跃响应 上升 时间/ ｍｓ 峰值 时间/ ｍｓ 调节 时间/ ｍｓ 超调 量/ ％ 突加负载 恢复 时间/ ｍｓ 速度 跌落/ ％ 继电 反馈 １９３ ４９９ １ １８５ ２０.０ １ ０９１ ３０.０ 模糊 控制 ７７ ２９０ １ ２４４ ６.１ ７２０ １７.３ 离线 整定 ９８ ３１５ ８１０ １４.１ １８７ １３.６ 混合 控制 ６６ １８３ ４３５ ８.７ ９８ １３.１ 由实验结果可以看出: １)继电反馈法整定出的 ＰＩ 参数在阶跃给定下 的响应时间长ꎬ超调量大ꎻ在突加负载时速度跌落 大ꎬ恢复时间最长. ２)在继电反馈法整定出的 ＰＩ 参数下ꎬ模糊控制 器可以很好地调整系统ꎬ其在阶跃响应下的超调量 最小ꎬ上升时间也仅次于混合控制ꎬ但其调节时间太 长ꎬ容易引起振荡ꎻ在突加负载时速度跌落小于继电 反馈法ꎬ但恢复时间也较长. ３)基于模型的离线整定法计算出的 ＰＩ 参数在 阶跃给定下性能优于继电反馈法ꎬ超调量大于模糊 控制ꎬ但调节时间小于模糊控制ꎻ在突加负载时性能 优于继电反馈法和模糊控制. ４)本文提出的混合控制方法ꎬ既使采用动态性 能比较折衷的参数选择ꎬ其在阶跃响应和突加负载 实验中的综合性能都优于其他方法ꎬ完全满足对调 速系统性能要求较高的应用. ３ 结束语 本文提出了基于模型的离线式整定与模糊 ＰＩ 在线整定相结合的混合整定法.通过分析矢量控制 原理推导出交流调速系统的数学模型ꎬ根据数学模 型计算 ＰＩ 参数和内环补偿量.然后构建了模糊 ＰＩ 控制器ꎬ根据实际调试经验提出了新的 ＰＩ 控制规 则.在混合整定过程中ꎬ可根据实际需求更改相应的 性能参数 ζ 和 Ｈ.最后通过实验证明了 ＰＩ 参数混合 整定法与其他方法相比能极大地提高系统的动态性 能和稳态精度ꎬ是一种优秀的 ＰＩ 参数整定方法.但 提出的方法需手动修改性能参数ꎬ若在不同阶段需 要不同的性能ꎬ则该系统难以实现.因此在以后的研 究中可尝试加入自适应控制ꎬ使得性能参数的修改 更为智能化、自动化ꎻ而且也可尝试其他智能算法替 代模糊控制算法ꎬ以求更高的系统性能. 参考文献: [１]王伟ꎬ张晶涛ꎬ柴天佑.ＰＩＤ 参数先进整定方法综述[ Ｊ]. 自动化学报ꎬ ２０００ꎬ ２６(３): ３４８￣３５５. ＷＡＮＧ Ｗｅｉꎬ ＺＨＡＮＧ Ｊｉｎｇｔａｏꎬ ＣＨＡＩ Ｔｉａｎｙｏｕ. Ａ ｓｕｒｖｅｙ ｏｆ ａｄｖａｎｃｅｄ ＰＩＤ ｐａｒａｍｅｔｅｒ ｔｕｎｉｎｇ ｍｅｔｈｏｄｓ[Ｊ]. Ａｃｔａ Ａｕｔｏｍａｔ￣ ｉｃａ Ｓｉｎｉｃａꎬ ２０００ꎬ ２６(３): ３４８￣３５５. [２]何颖ꎬ鹿蕾ꎬ赵争鸣.ＰＩＤ 参数自整定方法概述[ Ｊ].现代 电子技术ꎬ ２００４(２４): ２０￣２３. ＨＥ Ｙｉｎｇꎬ ＬＵ Ｌｅｉꎬ ＺＨＡＯ Ｚｈｅｎｇｍｉｎｇ. Ａ ｓｕｍｍａｒｉｚａｔｉｏｎ ｏｆ ＰＩＤ ｐａｒａｍｅｔｅｒｓ ａｕｔｏ￣ｔｕｎｉｎｇ ｍｅｔｈｏｄｓ[Ｊ]. Ｍｏｄｅｒｎ Ｅｌｅｃｔｒｏｎｉｃ Ｔｅｃｈｎｉｑｕｅꎬ ２００４(２４): ２０￣２３. [３]贺徽ꎬ周建中ꎬ谭建华ꎬ等.基于 Ｍａｍｄａｎｉ 模糊 ＰＩＤ 的同步 发电机励磁控制[ Ｊ].华中科技大学学报:自然科学版ꎬ ２０１０ꎬ ３８(２): ３４￣３７. ＨＥ Ｈｕｉꎬ ＺＨＯＵ Ｊｉａｎｚｈｏｎｇꎬ ＴＡＮ Ｊｉａｎｈｕａꎬ ｅｔ ａｌ. Ｒｅｓｅａｒｃｈ ａｎｄ ａｐｐｌｉｃａｔｉｏｎ ｏｆ ａ ｆｕｚｚｙ ＰＩＤ ｃｏｎｔｒｏｌｌｅｒ ｆｏｒ ｅｘｃｉｔａｔｉｏｎ ｃｏｎ￣ ｔｒｏｌ ｓｙｓｔｅｍｓ ｉｎ ｓｙｎｃｈｒｏｎｏｕｓ ｇｅｎｅｒａｔｏｒｓ ｕｓｉｎｇ Ｍａｍｄａｎｉ ｍｏｄｅｌ [Ｊ]. Ｊｏｕｒｎａｌ ｏｆ Ｈｕａｚｈｏｎｇ Ｕｎｉｖｅｒｓｉｔｙ ｏｆ Ｓｃｉｅｎｃｅ ａｎｄ Ｔｅｃｈ￣ ｎｏｌｏｇｙ: Ｎａｔｕｒｅ Ｓｃｉｅｎｃｅ Ｅｄｉｔｉｏｎꎬ ２０１０ꎬ ３８(２): ３４￣３７. [４]曹青松ꎬ周继惠ꎬ黎林ꎬ等.基于模糊自整定 ＰＩＤ 算法的压 第 ５ 期 李鹏ꎬ等:ＰＩ 参数混合整定法在闭环矢量控制系统中的应用 􀅰４５１􀅰

.452. 智能系统学报 第8卷 电柔性机械臂振动控制研究[J].振动与冲击，2010,29 [12]方斌时滞系统PD控制器增益的稳定范围研究[J].信 (12):181-186. 息与控制，2009,38(5)：546-551. CAO Qingsong,ZHOU Jihui,LI Lin,et al.Vibration con- FANG Bin.On gain stabilizing regions of PID controller for trol of piezoelectric flexible manipulator based on fuzzy self- time delay systems[J.Information and Control,2009,38 tuning PID algorithm[J].Journal of Vibration and Shock, (5)：546-551. 2010,29(12):181-186. [13]苏位峰.异步电机自抗扰矢量控制调速系统[D]北京： [5]刘国海，杨官学.基于神经网络广义逆的感应电机变频系 清华大学，2004. 统内模控制[J].江苏大学学报：自然科学版，2010,31 SU Weifeng.Active disturbances rejection control of field- (1):63-67 oriented induction motor drive system[]].Beijing:Tsing- LIU Guohai,YANG Guanxue.Internal model control of in- hua University,2004. duction motor variable frequency speed control system based [14]胡寿松.自动控制原理[M].北京：科学出版社，2007. on neural network generalized inverse[J].Journal of Jiangsu 作者简介： University:Natural Science Edition,2010,31(1):63-67. 李鹏，男，1981年生，工程师，主要 [6]张文辉，马静，高九州.基于神经网络的空间柔性机械臂 研究方向为机器人技术、电气传动技 PID快速学习控制[J].应用科技，2011,38(5)：14. 术.发表学术论文15篇，其中被SCI检 ZHANG Wenhui,MA Jing,GAO Jiuzhou.Fast learning 索1篇、E检索11篇，授权专利2项. PID control over space flexible manipulators based on neural network[J].Applied Science and Technology,2011,38 (5):1-4. [7]李庆春，沈德耀.一种PID模糊控制器(fuz四PI+fuzD 王胜勇，男，1971年生，高级工程 型)[J].控制与决策，2009,24(7)：1038-1042 师，主要研究方向为冶金自动化技术 LI Qingchun,SHEN Deyao.Brand-new PID fuzzy controller 曾获国家科技进步一等奖、国家优秀工 fuzzy PI+fuzzy ID)J].Control and Decision,2009,24 程设计奖及7项行业设计奖，发表学术 (7):1038-1042. 论文4篇，授权专利10项. [8]王秀君，胡协和.一种改进的单神经元PD控制策略[J]. 浙江大学学报：工学版，2011,45(8)：1498-1501 WANG Xiujun,HU Xiehe.An improved control strategy of 卢家斌，男，1965年生，高级工程 single neuron PID[J].Journal of Zhejiang University:Engi- 师，主要研究方向为冶金自动化技术。 neering Science,2011,45(8):1498-1501. 发表学术论文3篇授权专利10项. [9]MOHAN B M,SINHA A.The simplest fuzzy PID control- lers:mathematical models and stability analysis[J].Soft Computing,2006,10(10):961-975. [10]CHEN Y Q,MOORE K L.Relay feedback tuning of robust PID controllers with iso-damping property[J].IEEE 黄心汉.男，1946年生，教授，博士 Transactions on Systems,Man,and Cybernetics,Part B: 生导师，主要研究方向为智能控制、智 Cybernetics,2005,35(1):23-31. 能机器人、多传感器集成与信息融合、 [11]JENG J C,HUANG H P,LIN F Y.Modified relay feed- 图像处理与模式识别等.主持了国家自 back approach for controller tuning based on assessment of 然科学基金项目5项、国家“863”计划 gain and phase margins[J].Industrial and Engineering 项目4项和部级项目多项.发表学术论文 Chemistry Research,2006,45(12):4043-4051. 200余篇，出版专著1部，授权专利7项

电柔性机械臂振动控制研究[ Ｊ].振动与冲击ꎬ ２０１０ꎬ ２９ (１２): １８１￣１８６. ＣＡＯ Ｑｉｎｇｓｏｎｇꎬ ＺＨＯＵ Ｊｉｈｕｉꎬ ＬＩ Ｌｉｎꎬ ｅｔ ａｌ. Ｖｉｂｒａｔｉｏｎ ｃｏｎ￣ ｔｒｏｌ ｏｆ ｐｉｅｚｏｅｌｅｃｔｒｉｃ ｆｌｅｘｉｂｌｅ ｍａｎｉｐｕｌａｔｏｒ ｂａｓｅｄ ｏｎ ｆｕｚｚｙ ｓｅｌｆ￣ ｔｕｎｉｎｇ ＰＩＤ ａｌｇｏｒｉｔｈｍ[ Ｊ]. Ｊｏｕｒｎａｌ ｏｆ Ｖｉｂｒａｔｉｏｎ ａｎｄ Ｓｈｏｃｋꎬ ２０１０ꎬ ２９(１２): １８１￣１８６. [５]刘国海ꎬ杨官学.基于神经网络广义逆的感应电机变频系 统内模控制[ Ｊ].江苏大学学报:自然科学版ꎬ ２０１０ꎬ ３１ (１): ６３￣６７. ＬＩＵ Ｇｕｏｈａｉꎬ ＹＡＮＧ Ｇｕａｎｘｕｅ. Ｉｎｔｅｒｎａｌ ｍｏｄｅｌ ｃｏｎｔｒｏｌ ｏｆ ｉｎ￣ ｄｕｃｔｉｏｎ ｍｏｔｏｒ ｖａｒｉａｂｌｅ ｆｒｅｑｕｅｎｃｙ ｓｐｅｅｄ ｃｏｎｔｒｏｌ ｓｙｓｔｅｍ ｂａｓｅｄ ｏｎ ｎｅｕｒａｌ ｎｅｔｗｏｒｋ ｇｅｎｅｒａｌｉｚｅｄ ｉｎｖｅｒｓｅ[Ｊ]. Ｊｏｕｒｎａｌ ｏｆ Ｊｉａｎｇｓｕ Ｕｎｉｖｅｒｓｉｔｙ: Ｎａｔｕｒａｌ Ｓｃｉｅｎｃｅ Ｅｄｉｔｉｏｎꎬ ２０１０ꎬ ３１(１): ６３￣６７. [６]张文辉ꎬ马静ꎬ高九州.基于神经网络的空间柔性机械臂 ＰＩＤ 快速学习控制[Ｊ].应用科技ꎬ ２０１１ꎬ ３８(５): １￣４. ＺＨＡＮＧ Ｗｅｎｈｕｉꎬ ＭＡ Ｊｉｎｇꎬ ＧＡＯ Ｊｉｕｚｈｏｕ. Ｆａｓｔ ｌｅａｒｎｉｎｇ ＰＩＤ ｃｏｎｔｒｏｌ ｏｖｅｒ ｓｐａｃｅ ｆｌｅｘｉｂｌｅ ｍａｎｉｐｕｌａｔｏｒｓ ｂａｓｅｄ ｏｎ ｎｅｕｒａｌ ｎｅｔｗｏｒｋ[ Ｊ]. Ａｐｐｌｉｅｄ Ｓｃｉｅｎｃｅ ａｎｄ Ｔｅｃｈｎｏｌｏｇｙꎬ ２０１１ꎬ ３８ (５): １￣４. [７]李庆春ꎬ沈德耀.一种 ＰＩＤ 模糊控制器( ｆｕｚｚｙ ＰＩ＋ｆｕｚｚｙ ＩＤ 型)[Ｊ].控制与决策ꎬ ２００９ꎬ ２４(７): １０３８￣１０４２. ＬＩ Ｑｉｎｇｃｈｕｎꎬ ＳＨＥＮ Ｄｅｙａｏ. Ｂｒａｎｄ￣ｎｅｗ ＰＩＤ ｆｕｚｚｙ ｃｏｎｔｒｏｌｌｅｒ (ｆｕｚｚｙ ＰＩ＋ｆｕｚｚｙ ＩＤ) [ Ｊ]. Ｃｏｎｔｒｏｌ ａｎｄ Ｄｅｃｉｓｉｏｎꎬ ２００９ꎬ ２４ (７): １０３８￣１０４２. [８]王秀君ꎬ胡协和.一种改进的单神经元 ＰＩＤ 控制策略[ Ｊ]. 浙江大学学报:工学版ꎬ ２０１１ꎬ ４５(８): １４９８￣１５０１. ＷＡＮＧ Ｘｉｕｊｕｎꎬ ＨＵ Ｘｉｅｈｅ. Ａｎ ｉｍｐｒｏｖｅｄ ｃｏｎｔｒｏｌ ｓｔｒａｔｅｇｙ ｏｆ ｓｉｎｇｌｅ ｎｅｕｒｏｎ ＰＩＤ[Ｊ]. Ｊｏｕｒｎａｌ ｏｆ Ｚｈｅｊｉａｎｇ Ｕｎｉｖｅｒｓｉｔｙ: Ｅｎｇｉ￣ ｎｅｅｒｉｎｇ Ｓｃｉｅｎｃｅꎬ ２０１１ꎬ ４５(８): １４９８￣１５０１. [９]ＭＯＨＡＮ Ｂ Ｍꎬ ＳＩＮＨＡ Ａ. Ｔｈｅ ｓｉｍｐｌｅｓｔ ｆｕｚｚｙ ＰＩＤ ｃｏｎｔｒｏｌ￣ ｌｅｒｓ: ｍａｔｈｅｍａｔｉｃａｌ ｍｏｄｅｌｓ ａｎｄ ｓｔａｂｉｌｉｔｙ ａｎａｌｙｓｉｓ [ Ｊ]. Ｓｏｆｔ Ｃｏｍｐｕｔｉｎｇꎬ ２００６ꎬ １０(１０): ９６１￣９７５. [１０]ＣＨＥＮ Ｙ Ｑꎬ ＭＯＯＲＥ Ｋ Ｌ. Ｒｅｌａｙ ｆｅｅｄｂａｃｋ ｔｕｎｉｎｇ ｏｆ ｒｏｂｕｓｔ ＰＩＤ ｃｏｎｔｒｏｌｌｅｒｓ ｗｉｔｈ ｉｓｏ￣ｄａｍｐｉｎｇ ｐｒｏｐｅｒｔｙ[Ｊ]. ＩＥＥＥ Ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ Ｓｙｓｔｅｍｓꎬ Ｍａｎꎬ ａｎｄ Ｃｙｂｅｒｎｅｔｉｃｓꎬ Ｐａｒｔ Ｂ: Ｃｙｂｅｒｎｅｔｉｃｓꎬ ２００５ꎬ ３５(１): ２３￣３１. [１１]ＪＥＮＧ Ｊ Ｃꎬ ＨＵＡＮＧ Ｈ Ｐꎬ ＬＩＮ Ｆ Ｙ. Ｍｏｄｉｆｉｅｄ ｒｅｌａｙ ｆｅｅｄ￣ ｂａｃｋ ａｐｐｒｏａｃｈ ｆｏｒ ｃｏｎｔｒｏｌｌｅｒ ｔｕｎｉｎｇ ｂａｓｅｄ ｏｎ ａｓｓｅｓｓｍｅｎｔ ｏｆ ｇａｉｎ ａｎｄ ｐｈａｓｅ ｍａｒｇｉｎｓ [ Ｊ]. Ｉｎｄｕｓｔｒｉａｌ ａｎｄ Ｅｎｇｉｎｅｅｒｉｎｇ Ｃｈｅｍｉｓｔｒｙ Ｒｅｓｅａｒｃｈꎬ ２００６ꎬ ４５(１２): ４０４３￣４０５１. [１２]方斌.时滞系统 ＰＩＤ 控制器增益的稳定范围研究[ Ｊ].信 息与控制ꎬ ２００９ꎬ ３８(５): ５４６￣５５１. ＦＡＮＧ Ｂｉｎ. Ｏｎ ｇａｉｎ ｓｔａｂｉｌｉｚｉｎｇ ｒｅｇｉｏｎｓ ｏｆ ＰＩＤ ｃｏｎｔｒｏｌｌｅｒ ｆｏｒ ｔｉｍｅ ｄｅｌａｙ ｓｙｓｔｅｍｓ[Ｊ]. Ｉｎｆｏｒｍａｔｉｏｎ ａｎｄ Ｃｏｎｔｒｏｌꎬ ２００９ꎬ ３８ (５): ５４６￣５５１. [１３]苏位峰.异步电机自抗扰矢量控制调速系统[Ｄ].北京: 清华大学ꎬ ２００４. ＳＵ Ｗｅｉｆｅｎｇ. Ａｃｔｉｖｅ ｄｉｓｔｕｒｂａｎｃｅｓ ｒｅｊｅｃｔｉｏｎ ｃｏｎｔｒｏｌ ｏｆ ｆｉｅｌｄ￣ ｏｒｉｅｎｔｅｄ ｉｎｄｕｃｔｉｏｎ ｍｏｔｏｒ ｄｒｉｖｅ ｓｙｓｔｅｍ[ Ｊ]. Ｂｅｉｊｉｎｇ: Ｔｓｉｎｇ￣ ｈｕａ Ｕｎｉｖｅｒｓｉｔｙꎬ ２００４. [１４]胡寿松.自动控制原理[Ｍ].北京:科学出版社ꎬ ２００７. 作者简介: 李鹏ꎬ男ꎬ１９８１ 年生ꎬ工程师ꎬ主要 研究方向为机器人技术、电气传动技 术.发表学术论文 １５ 篇ꎬ其中被 ＳＣＩ 检 索 １ 篇、ＥＩ 检索 １１ 篇ꎬ授权专利 ２ 项. 王胜勇ꎬ男ꎬ１９７１ 年生ꎬ高级工程 师ꎬ主要研究方向为冶金自动化技术. 曾获国家科技进步一等奖、国家优秀工 程设计奖及 ７ 项行业设计奖ꎬ发表学术 论文 ４ 篇ꎬ授权专利 １０ 项. 卢家斌ꎬ男ꎬ１９６５ 年生ꎬ高级工程 师ꎬ主要研究方向为冶金自动化技术. 发表学术论文 ３ 篇ꎬ授权专利 １０ 项. 黄心汉ꎬ男ꎬ１９４６ 年生ꎬ教授ꎬ博士 生导师ꎬ主要研究方向为智能控制、智 能机器人、多传感器集成与信息融合、 图像处理与模式识别等.主持了国家自 然科学基金项目 ５ 项、国家“８６３”计划 项目 ４ 项和部级项目多项.发表学术论文 ２００ 余篇ꎬ出版专著 １ 部ꎬ授权专利 ７ 项. 􀅰４５２􀅰 智 能 系 统 学 报 第 ８ 卷