机器学习：一种优化神经网络的教与学优化算法

第8卷第4期 智能系统学报 Vol.8 No.4 2013年8月 CAAI Transactions on Intelligent Systems Aug.2013 D0I:10.3969/j.issn.1673-4785.201305026 网络出版地址：http://www.cnki.net/kcms/detail/23.1538.TP.20130827.1104.002.html 一种优化神经网络的教与学优化算法 拓守恒 (陕西理工学院数学与计算机科学学院，陕西汉中723001) 摘要：为了提高B即神经网络的输出精度，提出一种改进的教与学优化算法进行神经网络中的权值和阈值的优化 调整算法对基本的教与学优化算法的“教”阶段和“学”阶段分别进行改进，并提出一种“自学”机制来增强算法的学 习能力通过函数拟合实验和拖拉机齿轮箱故障诊断实验进行算法性能测试，结果表明，与遗传算法和基本的教与学 优化算法相比，该算法具有收敛速度快、求解精度高等优势： 关键词：改进的教与学优化算法；“自学”机制：神经网络；函数拟合；齿轮箱故障诊断 中图分类号：TP31文献标志码：A文章编号：1673-4785(2013)04-0327-06 中文引用格式：拓守恒.一种优化神经网络的教与学优化算法[J].智能系统学报，2013,8(4)：327-332. 英文引用格式：TUO Shouheng..A modified teaching-.learning-based optimization algorithm and application in neural networks[J] CAAI Transactions on Intelligent Systems,2013,8(4):327-332. A modified teaching-learning-based optimization algorithm and application in neural networks TUO Shouheng (School of Mathematics and Computer Science,Shaanxi University of Technology,Hanzhong 723001,China) Abstract:In order to improve the output accuracy of back propagation neural network,a modified teaching-learn- ing-based optimization MTLBO)algorithm is proposed to train the weight and threshold value of neural network.In the MTLBO method,the "Teaching"phase and "Learning"phase were modified on the basis of TLBO algorithm, and a new "Self-Learning"mechanism was proposed to intensify global searching ability.Finally,the function fit- ting experiment and the tractor gearbox diagnosis experiment were used to test the performance of the proposed algo- rithm.Simulations show that this algorithm has a better convergence,prediction accuracy and robustness compared to the genetic algorithm (GA)and the basic teaching-learning-based optimization (TLBO)algorithm. Keywords:modified teaching-learning-based optimization algorithm;"self-learning"mechanism;neural network; function fitting;gearbox fault diagnosis 近年来，神经网络(neural network,NN)受到很 输出和问题的实际输出值之间的误差尽可能小.因 多学者的关注，它的应用取得了很好的成效.NN为 此如何调节网络连接权值就成为确定BP神经网络 解决大规模复杂问题提供了一种简单易行的方法， 结构的重点.目前，对神经网络的优化主要是梯度优 被广泛用于模式识别等分类和预测问题.BP(back 化技术，如反向传播学习算法.反向传播学习算 propagation)神经网络结构划分为输入层、隐含层和 法[1]在神经网络中得到了广泛的应用，BP神经网 输出层输人层节点用于接收一组预测变量，输出层 络由信息的正向传播和误差的反向传播2个过程组 节点输出相应的目标值（目标值可以不止一个）.BP 成.输入层各神经元负责接收来自外界的输入信息， 神经网络构建的主要工作是通过调节连接输入层、 并传递给中间层各神经元：中间层是内部信息处理 隐含层和输出层之间的连接权值，使得神经网络的 层，负责信息变换，根据信息变化能力的需求，中间 层可以设计为单隐层或者多隐层结构：最后一个隐 收稿日期：2013-05-09.网络出版日期：2013-08-27 基金项目：陕西省教育厅科研计划资助项目(12K0863):陕西理工科 层传递到输出层各神经元的信息，经进一步处理后， 研项目(SLGKY12-16). 通信作者：拓守恒.E-mail:tmo_sh@126.com 完成一次学习的正向传播处理过程，由输出层向外

第 ８ 卷第 ４ 期 智 能 系 统 学 报 Ｖｏｌ．８ №．４ ２０１３ 年 ８ 月 ＣＡＡＩ Ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ Ｉｎｔｅｌｌｉｇｅｎｔ Ｓｙｓｔｅｍｓ Ａｕｇ． ２０１３ ＤＯＩ：１０．３９６９ ／ ｊ．ｉｓｓｎ．１６７３⁃４７８５．２０１３０５０２６ 网络出版地址：ｈｔｔｐ： ／ ／ ｗｗｗ．ｃｎｋｉ．ｎｅｔ ／ ｋｃｍｓ／ ｄｅｔａｉｌ ／ ２３．１５３８．ＴＰ．２０１３０８２７．１１０４．００２．ｈｔｍｌ 一种优化神经网络的教与学优化算法 拓守恒 （陕西理工学院 数学与计算机科学学院， 陕西 汉中 ７２３００１） 摘 要：为了提高 ＢＰ 神经网络的输出精度，提出一种改进的教与学优化算法进行神经网络中的权值和阈值的优化 调整．算法对基本的教与学优化算法的“教”阶段和“学”阶段分别进行改进，并提出一种“自学”机制来增强算法的学 习能力．通过函数拟合实验和拖拉机齿轮箱故障诊断实验进行算法性能测试，结果表明，与遗传算法和基本的教与学 优化算法相比，该算法具有收敛速度快、求解精度高等优势． 关键词：改进的教与学优化算法； “自学”机制；神经网络；函数拟合；齿轮箱故障诊断 中图分类号：ＴＰ３１ 文献标志码：Ａ 文章编号：１６７３⁃４７８５（２０１３）０４⁃０３２７⁃０６ 中文引用格式：拓守恒．一种优化神经网络的教与学优化算法［Ｊ］． 智能系统学报， ２０１３， ８（４）： ３２７⁃３３２． 英文引用格式：ＴＵＯ Ｓｈｏｕｈｅｎｇ． Ａ ｍｏｄｉｆｉｅｄ ｔｅａｃｈｉｎｇ⁃ｌｅａｒｎｉｎｇ⁃ｂａｓｅｄ ｏｐｔｉｍｉｚａｔｉｏｎ ａｌｇｏｒｉｔｈｍ ａｎｄ ａｐｐｌｉｃａｔｉｏｎ ｉｎ ｎｅｕｒａｌ ｎｅｔｗｏｒｋｓ［Ｊ］． ＣＡＡＩ Ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ Ｉｎｔｅｌｌｉｇｅｎｔ Ｓｙｓｔｅｍｓ， ２０１３， ８（４）： ３２７⁃３３２． Ａ ｍｏｄｉｆｉｅｄ ｔｅａｃｈｉｎｇ⁃ｌｅａｒｎｉｎｇ⁃ｂａｓｅｄ ｏｐｔｉｍｉｚａｔｉｏｎ ａｌｇｏｒｉｔｈｍ ａｎｄ ａｐｐｌｉｃａｔｉｏｎ ｉｎ ｎｅｕｒａｌ ｎｅｔｗｏｒｋｓ ＴＵＯ Ｓｈｏｕｈｅｎｇ （Ｓｃｈｏｏｌ ｏｆ Ｍａｔｈｅｍａｔｉｃｓ ａｎｄ Ｃｏｍｐｕｔｅｒ Ｓｃｉｅｎｃｅ， Ｓｈａａｎｘｉ Ｕｎｉｖｅｒｓｉｔｙ ｏｆ Ｔｅｃｈｎｏｌｏｇｙ， Ｈａｎｚｈｏｎｇ ７２３００１， Ｃｈｉｎａ） Ａｂｓｔｒａｃｔ：Ｉｎ ｏｒｄｅｒ ｔｏ ｉｍｐｒｏｖｅ ｔｈｅ ｏｕｔｐｕｔ ａｃｃｕｒａｃｙ ｏｆ ｂａｃｋ ｐｒｏｐａｇａｔｉｏｎ ｎｅｕｒａｌ ｎｅｔｗｏｒｋ， ａ ｍｏｄｉｆｉｅｄ ｔｅａｃｈｉｎｇ⁃ｌｅａｒｎ⁃ ｉｎｇ⁃ｂａｓｅｄ ｏｐｔｉｍｉｚａｔｉｏｎ （ＭＴＬＢＯ） ａｌｇｏｒｉｔｈｍ ｉｓ ｐｒｏｐｏｓｅｄ ｔｏ ｔｒａｉｎ ｔｈｅ ｗｅｉｇｈｔ ａｎｄ ｔｈｒｅｓｈｏｌｄ ｖａｌｕｅ ｏｆ ｎｅｕｒａｌ ｎｅｔｗｏｒｋ． Ｉｎ ｔｈｅ ＭＴＬＢＯ ｍｅｔｈｏｄ， ｔｈｅ “Ｔｅａｃｈｉｎｇ” ｐｈａｓｅ ａｎｄ “Ｌｅａｒｎｉｎｇ” ｐｈａｓｅ ｗｅｒｅ ｍｏｄｉｆｉｅｄ ｏｎ ｔｈｅ ｂａｓｉｓ ｏｆ ＴＬＢＯ ａｌｇｏｒｉｔｈｍ， ａｎｄ ａ ｎｅｗ “Ｓｅｌｆ⁃Ｌｅａｒｎｉｎｇ” ｍｅｃｈａｎｉｓｍ ｗａｓ ｐｒｏｐｏｓｅｄ ｔｏ ｉｎｔｅｎｓｉｆｙ ｇｌｏｂａｌ ｓｅａｒｃｈｉｎｇ ａｂｉｌｉｔｙ． Ｆｉｎａｌｌｙ， ｔｈｅ ｆｕｎｃｔｉｏｎ ｆｉｔ⁃ ｔｉｎｇ ｅｘｐｅｒｉｍｅｎｔ ａｎｄ ｔｈｅ ｔｒａｃｔｏｒ ｇｅａｒｂｏｘ ｄｉａｇｎｏｓｉｓ ｅｘｐｅｒｉｍｅｎｔ ｗｅｒｅ ｕｓｅｄ ｔｏ ｔｅｓｔ ｔｈｅ ｐｅｒｆｏｒｍａｎｃｅ ｏｆ ｔｈｅ ｐｒｏｐｏｓｅｄ ａｌｇｏ⁃ ｒｉｔｈｍ． Ｓｉｍｕｌａｔｉｏｎｓ ｓｈｏｗ ｔｈａｔ ｔｈｉｓ ａｌｇｏｒｉｔｈｍ ｈａｓ ａ ｂｅｔｔｅｒ ｃｏｎｖｅｒｇｅｎｃｅ， ｐｒｅｄｉｃｔｉｏｎ ａｃｃｕｒａｃｙ ａｎｄ ｒｏｂｕｓｔｎｅｓｓ ｃｏｍｐａｒｅｄ ｔｏ ｔｈｅ ｇｅｎｅｔｉｃ ａｌｇｏｒｉｔｈｍ （ＧＡ） ａｎｄ ｔｈｅ ｂａｓｉｃ ｔｅａｃｈｉｎｇ⁃ｌｅａｒｎｉｎｇ⁃ｂａｓｅｄ ｏｐｔｉｍｉｚａｔｉｏｎ （ＴＬＢＯ） ａｌｇｏｒｉｔｈｍ． Ｋｅｙｗｏｒｄｓ：ｍｏｄｉｆｉｅｄ ｔｅａｃｈｉｎｇ⁃ｌｅａｒｎｉｎｇ⁃ｂａｓｅｄ ｏｐｔｉｍｉｚａｔｉｏｎ ａｌｇｏｒｉｔｈｍ； “ ｓｅｌｆ⁃ｌｅａｒｎｉｎｇ” ｍｅｃｈａｎｉｓｍ； ｎｅｕｒａｌ ｎｅｔｗｏｒｋ； ｆｕｎｃｔｉｏｎ ｆｉｔｔｉｎｇ； ｇｅａｒｂｏｘ ｆａｕｌｔ ｄｉａｇｎｏｓｉｓ 收稿日期：２０１３⁃０５⁃０９． 网络出版日期：２０１３⁃０８⁃２７． 基金项目：陕西省教育厅科研计划资助项目（１２ＪＫ０８６３）；陕西理工科 研项目（ＳＬＧＫＹ １２⁃１６）． 通信作者：拓守恒． Ｅ⁃ｍａｉｌ：ｔｕｏ＿ｓｈ＠ １２６．ｃｏｍ． 近年来，神经网络（ ｎｅｕｒａｌ ｎｅｔｗｏｒｋ，ＮＮ）受到很 多学者的关注，它的应用取得了很好的成效．ＮＮ 为 解决大规模复杂问题提供了一种简单易行的方法， 被广泛用于模式识别等分类和预测问题．ＢＰ （ ｂａｃｋ ｐｒｏｐａｇａｔｉｏｎ）神经网络结构划分为输入层、隐含层和 输出层．输入层节点用于接收一组预测变量，输出层 节点输出相应的目标值（目标值可以不止一个）．ＢＰ 神经网络构建的主要工作是通过调节连接输入层、 隐含层和输出层之间的连接权值，使得神经网络的 输出和问题的实际输出值之间的误差尽可能小．因 此如何调节网络连接权值就成为确定 ＢＰ 神经网络 结构的重点．目前，对神经网络的优化主要是梯度优 化技术， 如反向传播学习算法． 反向传播学习算 法［１⁃２］在神经网络中得到了广泛的应用，ＢＰ 神经网 络由信息的正向传播和误差的反向传播 ２ 个过程组 成．输入层各神经元负责接收来自外界的输入信息， 并传递给中间层各神经元；中间层是内部信息处理 层，负责信息变换，根据信息变化能力的需求，中间 层可以设计为单隐层或者多隐层结构；最后一个隐 层传递到输出层各神经元的信息，经进一步处理后， 完成一次学习的正向传播处理过程，由输出层向外

·328· 智能系统学报 第8卷 界输出信息处理结果.当实际输出与期望输出不符 习后的值，还有2个关键的参数：教学因子T℉，= 时，进入误差的反向传播阶段误差通过输出层，按 round[1+rand(0,1)]和学习步长r:=rand(0,1)用 误差梯度下降的方式修正各层权值，向隐层、输入层 于调整学习速率 逐层反传但是，梯度下降优化法存在不稳定和不可 1.2学员之间相互“学”阶段 预知的问题，并且对初始值非常敏感，对于多峰值优 在学员相互“学”阶段，每个学员X(i=1,2,…, 化问题，很容易陷入局部搜索而失去全局最优解.为 NP)在班级中随机选取一个学习对象X(j=1,2, 此，近年来，很多启发式智能全局优化算法被用于神 …,NP,j≠)，X,通过分析自己和学员X的差异进 经网络的优化设计，例如，遗传算法(genetic algo- 行学习调整，学习改进的方法类似于差分算法中的 rithm,GA)[)、粒子群优化算法(particle swarm opti-- 差分变异算子，不同在于，TLB0算法中的学习步长 mization,PSO)[)、模拟退火算法(simulated annea- r对每个学员采用不同的学习因子.采用式(3)实现 ling,SA)等.本文提出一种改进的教与学优化算法 “学”的过程 teaching-learning-based optimization,TLBO)[561 (X+·(X:-X),X优于X: 行BP神经网络的优化设计. (3) X+r·(X-X),X优于X 1教与学优化算法 式中：=U(0,1)表示第i个学员的学习因子（学习 教与学优化算法由印度学者R.V.Rao和V.D. 步长) Kalyankar于2010年提出，TLBO算法通过模拟人类 1.3学员更新 在学习过程中的老师“教”和学生相互“学”2个阶 学员经过“教”阶段和“学”阶段都要分别进行 段的学习方法，促进每个学员的学习水平， 更新操作更新方法如下： 基本的TLBO算法是模拟以“班级”为单位的学 If X is better than Xod, 习方式，班级中学员水平的提高需要教师的“教”来 X=X", 引导，同时，学员之间需要相互“学习”交流来促进 End If. 知识的进步其中，教师和学员相当于进化算法中的 2 改进的教与学优化算法 个体，而教师是适应值最好的个体之一.每个学员所 学的某一科目相当于一个决策变量 对低维单模优化问题，基本的TLB0算法的收 下面是几个基本定义： 敛速度很快，求解精度很高，运行代价较小，算法的 1)学习知识范围（对应于搜索区域）.学员所学 时间复杂度为O(NP×T),(NP是学员数量，T是最 知识范围定义为X=(x,x2,…,x4)∈[L,U],L= 大允许迭代次数).TLBO算法的缺点是，对于高维 (L,2,…,L)是空间下届，U=(U,U2,…,)是 “多模态”的复杂优化问题，全局探索能力较差，很 空间上届，d是学员所学科目数（对应于优化问题的 容易陷入局部搜索而丢失全局最优解.主要原因是 维数) TLB0算法在“教”阶段对所有学员采用相同的差异 2)班级：所有学员的集合称为班级（种群） 值Difference进行调整，使得算法的搜索策略比较单 3)教师：班级中水平最高的个体称为教师，记 一，学员很容易快速向“老师”聚集，导致学员知识 为icacher或Xen 多样性的快速丢失，从而陷入局部搜索.这样，对于 4)学员（个体）：班级中第i个学员定义为X= 高维“多模态”问题，TLB0算法往往会丢失全局最 (x,x,…,x),其中，(=1,2，…，d)表示学员X 优解而获得局部最优解8】」 所学的第j门课程， 在TLB0算法中，学员的学习过程完全依赖老师 1.1教师的“教”阶段 的“教”和学员之间的交流“学习”，造成学员在学习 在TLBO算法的“教”阶段，班级中每个学员X 过程中对他人的过度依赖，但却丧失了学习过程中自 (i=l,2,…,NP)根据Xaa和班级中学员平均水平 我学习和自我创新能力的挖掘.因此，为了发挥群体 中每个学员的智慧和才能，本文针对TLB0算法的缺 值Mean=(∑X,)/NP之间的差异性进行学习.采 陷，提出一种改进的教与学优化算法(modified teach- 用式(1)~(2)实现“教”的过程. ing-learning-based optimization,MTLBO),算法借鉴和 X.=Xal Difference, (1) 声搜索算法思想进行个体的自我学习和自我探索创 Difference=r:·(Ktacher-TF:·Mean).(2) 新能力挖掘，用于加强每个个体的自我局部搜索能 式中：xX“和X"分别表示第i个学员学习前和学 力，从而增加种群的全局探索能力

界输出信息处理结果．当实际输出与期望输出不符 时，进入误差的反向传播阶段．误差通过输出层，按 误差梯度下降的方式修正各层权值，向隐层、输入层 逐层反传．但是，梯度下降优化法存在不稳定和不可 预知的问题，并且对初始值非常敏感，对于多峰值优 化问题，很容易陷入局部搜索而失去全局最优解．为 此，近年来，很多启发式智能全局优化算法被用于神 经网络的优化设计，例如，遗传算法（ ｇｅｎｅｔｉｃ ａｌｇｏ⁃ ｒｉｔｈｍ， ＧＡ） ［３］ 、粒子群优化算法（ｐａｒｔｉｃｌｅ ｓｗａｒｍ ｏｐｔｉ⁃ ｍｉｚａｔｉｏｎ， ＰＳＯ） ［４］ 、模拟退火算法（ ｓｉｍｕｌａｔｅｄ ａｎｎｅａ⁃ ｌｉｎｇ， ＳＡ）等．本文提出一种改进的教与学优化算法 （ ｔｅａｃｈｉｎｇ⁃ｌｅａｒｎｉｎｇ⁃ｂａｓｅｄ ｏｐｔｉｍｉｚａｔｉｏｎ， ＴＬＢＯ） ［５⁃６］ 进 行 ＢＰ 神经网络的优化设计． １ 教与学优化算法 教与学优化算法由印度学者 Ｒ．Ｖ．Ｒａｏ 和 Ｖ．Ｄ． Ｋａｌｙａｎｋａｒ 于 ２０１０ 年提出，ＴＬＢＯ 算法通过模拟人类 在学习过程中的老师“教”和学生相互“学” ２ 个阶 段的学习方法，促进每个学员的学习水平． 基本的 ＴＬＢＯ 算法是模拟以“班级”为单位的学 习方式，班级中学员水平的提高需要教师的“教”来 引导，同时，学员之间需要相互“学习” 交流来促进 知识的进步．其中，教师和学员相当于进化算法中的 个体，而教师是适应值最好的个体之一．每个学员所 学的某一科目相当于一个决策变量． 下面是几个基本定义： １） 学习知识范围（对应于搜索区域）．学员所学 知识范围定义为 Ｘ ＝ （ｘ １ ，ｘ ２ ，…，ｘ ｄ ）∈ ［ Ｌ，Ｕ］ ，Ｌ ＝ （Ｌ １ ，Ｌ ２ ，…，Ｌ ｄ ）是空间下届，Ｕ＝ （Ｕ １ ，Ｕ ２ ，…，Ｕ ｄ ） 是 空间上届，ｄ 是学员所学科目数（对应于优化问题的 维数）． ２） 班级：所有学员的集合称为班级（种群）． ３） 教师：班级中水平最高的个体称为教师，记 为 Ｘｔｅａｃｈｅｒ或 Ｘｂｅｓｔ ． ４） 学员（个体）： 班级中第 ｉ 个学员定义为Ｘｉ ＝ （ｘ １ ｉ ，ｘ ２ ｉ ，…，ｘ ｄ ｉ ），其中，ｘ ｊ ｉ（ｊ ＝ １，２，…，ｄ）表示学员 Ｘｉ 所学的第 ｊ 门课程． １．１ 教师的“教”阶段 在 ＴＬＢＯ 算法的“教”阶段，班级中每个学员 Ｘｉ （ｉ ＝ １，２，…，ＮＰ）根据 Ｘｔｅａｃｈｅｒ和班级中学员平均水平 值 Ｍｅａｎ ＝ （∑ ＮＰ ｉ ＝ １ Ｘｉ） ／ ＮＰ 之间的差异性进行学习．采 用式（１） ～ （２）实现“教”的过程． Ｘ ｎｅｗ ｉ ＝ Ｘ ｏｌｄ ｉ ＋ Ｄｉｆｆｅｒｅｎｃｅ， （１） Ｄｉｆｆｅｒｅｎｃｅ ＝ ｒｉ·（Ｘｔｅａｃｈｅｒ － ＴＦｉ·Ｍｅａｎ）． （２） 式中：Ｘ ｏｌｄ ｉ 和 Ｘ ｎｅｗ ｉ 分别表示第 ｉ 个学员学习前和学 习后的值，还有 ２ 个关键的参数：教学因子 ＴＦｉ ＝ ｒｏｕｎｄ [１＋ｒａｎｄ（０，１） ] 和学习步长 ｒｉ ＝ ｒａｎｄ（０，１） 用 于调整学习速率． １．２ 学员之间相互“学”阶段 在学员相互“学”阶段，每个学员 Ｘｉ（ｉ ＝ １，２，…， ＮＰ）在班级中随机选取一个学习对象 Ｘｊ（ ｊ ＝ １，２， …，ＮＰ，ｊ≠ｉ），Ｘｉ 通过分析自己和学员 Ｘｊ 的差异进 行学习调整，学习改进的方法类似于差分算法中的 差分变异算子，不同在于，ＴＬＢＯ 算法中的学习步长 ｒ 对每个学员采用不同的学习因子．采用式（３）实现 “学”的过程． Ｘ ｎｅｗ ｉ ＝ Ｘ ｏｌｄ ｉ ＋ ｒｉ·（Ｘｉ － Ｘｊ）， Ｘｉ 优于 Ｘｊ； Ｘ ｏｌｄ ｉ ＋ ｒｉ·（Ｘｊ － Ｘｉ）， Ｘｊ 优于 Ｘｉ { ． （３） 式中：ｒｉ ＝Ｕ（０，１）表示第 ｉ 个学员的学习因子（学习 步长）． １．３ 学员更新 学员经过“教”阶段和“学”阶段都要分别进行 更新操作．更新方法如下： Ｉｆ Ｘ ｎｅｗ ｉ ｉｓ ｂｅｔｔｅｒ ｔｈａｎ Ｘ ｏｌｄ ｉ ， Ｘ ｏｌｄ ｉ ＝ Ｘ ｎｅｗ ｉ ， Ｅｎｄ Ｉｆ． ２ 改进的教与学优化算法 对低维单模优化问题，基本的 ＴＬＢＯ 算法的收 敛速度很快，求解精度很高，运行代价较小，算法的 时间复杂度为 Ｏ（ＮＰ ×Ｔ），（ＮＰ 是学员数量，Ｔ 是最 大允许迭代次数）． ＴＬＢＯ 算法的缺点是，对于高维 “多模态”的复杂优化问题，全局探索能力较差，很 容易陷入局部搜索而丢失全局最优解．主要原因是 ＴＬＢＯ 算法在“教”阶段对所有学员采用相同的差异 值 Ｄｉｆｆｅｒｅｎｃｅ 进行调整，使得算法的搜索策略比较单 一，学员很容易快速向“老师”聚集，导致学员知识 多样性的快速丢失，从而陷入局部搜索．这样，对于 高维“多模态”问题，ＴＬＢＯ 算法往往会丢失全局最 优解而获得局部最优解［７⁃８］ ． 在 ＴＬＢＯ 算法中，学员的学习过程完全依赖老师 的“教”和学员之间的交流“学习”，造成学员在学习 过程中对他人的过度依赖，但却丧失了学习过程中自 我学习和自我创新能力的挖掘．因此，为了发挥群体 中每个学员的智慧和才能，本文针对 ＴＬＢＯ 算法的缺 陷，提出一种改进的教与学优化算法（ｍｏｄｉｆｉｅｄ ｔｅａｃｈ⁃ ｉｎｇ⁃ｌｅａｒｎｉｎｇ⁃ｂａｓｅｄ ｏｐｔｉｍｉｚａｔｉｏｎ， ＭＴＬＢＯ），算法借鉴和 声搜索算法思想进行个体的自我学习和自我探索创 新能力挖掘，用于加强每个个体的自我局部搜索能 力，从而增加种群的全局探索能力． ·３２８· 智 能 系 统 学 报 第 ８ 卷

第4期 拓守恒：一种优化神经网络的教与学优化算法 ·329· 2.1改进的“教”阶段 弱，本文引入“自学”阶段，每个学员通过自学阶段， 本文通过对Mean进行改进，使Mean=(Xost+ 充分发挥每个学员的能力，增强算法的全局探索能 X)/2,这样计算的好处是Mean对每个个体X其值 力(exploration).本文中的“自学”阶段采用类似于作 都不同，从而保证种群的多样性，避免算法早熟，改 者提出的一种改进的和声算法[9思想进行. 进后的教学过程如下： 2.3“自我”学习阶段 For i=1:NP 在前面的“教”和相互“学”阶段，学习的对象是 TF=round [1+rand(1,d)], 学员整体进行，但是，由于每个学员都会学习多门科 Xe"=X,+rand(1,d)×[Xcacher-TF× 目（对应于搜索算法中的决策变量），学员学习时可 (Xm+X:)/2], 能会出现“偏科”现象，有些学员可能会部分科目学 End. 习较好，部分科目学习效果较差.因此，在“自学”阶 2.2改进的相互“学习”阶段 段，根据每个学员的特点对成绩不够理想的科目进 在相互“学习”阶段，TLB0算法中每个学员X 行针对性学习.采用3种学习策略对学员的某些科 (i=1,2,…,NP)每次随机选取另一个学习对象X 目进行自我学习调整：l)以学习率(learn from others (G=1,2,…,NP,≠i)进行学习.本文中，每次随机选 probability,LoP)选择学习对象；2)以概率(self re- 取2个学习对象X,和X,(r1=1,2,…,NP;r2=1,2, pair probability,SRP)进行自我学习方法调整；3)以 …,NP;1≠r2),通过比较X,和X,的优劣性并计算 概率(innovative learning probability,ILP)进行创新 二者的差异性进行学习，这样能够有效提高学习成 学习具体“自我”学习阶段的算法如下： 功率，避免“盲目学习”学习过程伪代码如下： For i=1 to NP For i=1:NP Forj=1tod//第i个学员开始“自我”学习 随机从种群中选择2个个体X,和X,(X,≠ If rand()<LoP/向他人学习 X,) xe=X,a∈U{1,2,…,NP}; Else If rand()<SRP/自我学习方法调整 If FITS(X,)<FITS(X) =rand(0,1)*Step(j); Y=2xX,-X Else If rand()<LP/创新学习 Else x=V+rand(0,1)×(U-); Y=2×X2-X,; Else End xhe=i 差异学习 End X=X+rand(1,d).x(Y-X) Xnn=(xn,x2n,…,xdn） End End rand(1,d)表示在[0,1]随机生成一个d维的 End 行向量 算法中，Step是自我学习调整步长，定义为 在本文算法的相互“学习"”阶段，与TLB0算法 Step=mins+(maxsp -minsp)(1-t/T). 不同的有： 式中：maxsup=(U-L)/50,minsp=(U-L)/3000,t 1)学习方法不同.根据文献[11]中的最好个体 是当前迭代次数，T是允许最大迭代次数： 与最差个体的差异性思想，算法首先利用2个随机 选择的学员作差异计算：Y=2×X,-X,,对X,修正后 3利用MTLBO算法进行函数优化 再次和学员X进行差异学习，使得算法具有更强的 3.1多峰值函数Schwefel2.26测试分析 自适应学习能力. 为了验证本文算法的性能，首先对一个经典的 2)更新操作不同.首先判断产生的新个体X 高维多峰值函数Schwefel2.26进行测试检验，将本 是否比原来的个体更好，如果是则用新个体替换原 文算法与GA和基本的TLBO算法进行比较，设置 个体，否则，再次判断新个体是否比种群中的最差个 函数维数d=100,种群大小NP=50,最大迭代次数 体X.优秀，如果是，则用X替换X. Tmx=5000.遗传算法参数：交叉概率cp=0.6,变异 由于算法在应用上述的“教”与“学”过程时，收 概率mp=0.1;本文算法参数：ToP=0.55,SRP=0.3, 敛速度很快，局部开发能力(exploitation)较强，种群 LP=0.1.为了公平起见，每个算法独立运行30次， 的多样性容易丢失，全局搜索能力(exploration)较 取其最优值，并统计其最佳解Best,最差解Worst,平

２．１ 改进的“教”阶段 本文通过对 Ｍｅａｎ 进行改进，使 Ｍｅａｎ ＝ （Ｘｗｏｒｓｔ ＋ Ｘｉ） ／ ２，这样计算的好处是 Ｍｅａｎ 对每个个体 Ｘｉ其值 都不同，从而保证种群的多样性，避免算法早熟，改 进后的教学过程如下： Ｆｏｒ ｉ ＝ １ ∶ ＮＰ ＴＦ ＝ ｒｏｕｎｄ [１＋ｒａｎｄ(１，ｄ) ] ， Ｘ ｎｅｗ ｉ ＝ Ｘｉ ＋ ｒａｎｄ （ １， ｄ ） × ［ Ｘｔｅａｃｈｅｒ － ＴＦ × Ｘｗｏｒｓｔ ＋Ｘｉ ( ) ／ ２］， Ｅｎｄ． ２．２ 改进的相互“学习”阶段 在相互“学习”阶段，ＴＬＢＯ 算法中每个学员 Ｘｉ （ｉ ＝ １，２，…，ＮＰ）每次随机选取另一个学习对象 Ｘｊ （ｊ ＝ １，２，…，ＮＰ，ｊ≠ｉ）进行学习．本文中，每次随机选 取 ２ 个学习对象 Ｘｒ １ 和 Ｘｒ ２ （ｒ１ ＝ １，２，…，ＮＰ；ｒ２ ＝ １，２， …，ＮＰ；ｒ１≠ｒ２ ），通过比较 Ｘｒ １ 和 Ｘｒ ２ 的优劣性并计算 二者的差异性进行学习，这样能够有效提高学习成 功率，避免“盲目学习”．学习过程伪代码如下： Ｆｏｒ ｉ ＝ １：ＮＰ 随机从种群中选择 ２ 个个体 Ｘｒ １ 和 Ｘｒ ２ （Ｘｒ １ ≠ Ｘｒ ２ ） Ｉｆ ＦＩＴＳ Ｘｒ １ ( ) ＜ＦＩＴＳ Ｘｒ ２ ( ) Ｙ ＝ ２×Ｘｒ １ －Ｘｒ ２ ； Ｅｌｓｅ Ｙ ＝ ２×Ｘｒ ２ －Ｘｒ １ ； Ｅｎｄ 差异学习 Ｘｎｅｗ ＝Ｘｉ ＋ｒａｎｄ(１，ｄ) ．× Ｙ－Ｘｉ ( ) ； Ｅｎｄ ｒａｎｄ（１，ｄ）表示在［０，１］随机生成一个 ｄ 维的 行向量． 在本文算法的相互“学习”阶段，与 ＴＬＢＯ 算法 不同的有： １）学习方法不同．根据文献［１１］中的最好个体 与最差个体的差异性思想，算法首先利用 ２ 个随机 选择的学员作差异计算：Ｙ ＝ ２×Ｘｒ １ －Ｘｒ ２ ，对 Ｘｒ 修正后 再次和学员 Ｘｉ进行差异学习，使得算法具有更强的 自适应学习能力． ２）更新操作不同．首先判断产生的新个体 Ｘｎｅｗ 是否比原来的个体更好，如果是则用新个体替换原 个体，否则，再次判断新个体是否比种群中的最差个 体 Ｘｗｏｒｓｔ优秀，如果是，则用 Ｘｎｅｗ替换 Ｘｗｏｒｓｔ ． 由于算法在应用上述的“教”与“学”过程时，收 敛速度很快，局部开发能力（ ｅｘｐｌｏｉｔａｔｉｏｎ）较强，种群 的多样性容易丢失，全局搜索能力（ ｅｘｐｌｏｒａｔｉｏｎ） 较 弱，本文引入“自学”阶段，每个学员通过自学阶段， 充分发挥每个学员的能力，增强算法的全局探索能 力（ｅｘｐｌｏｒａｔｉｏｎ）．本文中的“自学”阶段采用类似于作 者提出的一种改进的和声算法［９⁃１１］思想进行． ２．３ “自我”学习阶段 在前面的“教”和相互“学”阶段，学习的对象是 学员整体进行，但是，由于每个学员都会学习多门科 目（对应于搜索算法中的决策变量），学员学习时可 能会出现“偏科”现象，有些学员可能会部分科目学 习较好，部分科目学习效果较差．因此，在“自学”阶 段，根据每个学员的特点对成绩不够理想的科目进 行针对性学习．采用 ３ 种学习策略对学员的某些科 目进行自我学习调整：１）以学习率（ｌｅａｒｎ ｆｒｏｍ ｏｔｈｅｒｓ ｐｒｏｂａｂｉｌｉｔｙ， ＬｏＰ） 选择学习对象；２） 以概率（ ｓｅｌｆ ｒｅ⁃ ｐａｉｒ ｐｒｏｂａｂｉｌｉｔｙ， ＳＲＰ）进行自我学习方法调整；３）以 概率 （ｉｎｎｏｖａｔｉｖｅ ｌｅａｒｎｉｎｇ ｐｒｏｂａｂｉｌｉｔｙ， ＩＬＰ）进行创新 学习．具体“自我”学习阶段的算法如下： Ｆｏｒ ｉ ＝ １ ｔｏ ＮＰ Ｆｏｒ ｊ ＝ １ ｔｏ ｄ ／ ／ 第 ｉ 个学员开始“自我”学习 Ｉｆ ｒａｎｄ（）＜ＬｏＰ ／ ／ 向他人学习 ｘ ｊ ｎｅｗ ＝Ｘ ｊ ａ ，ａ∈Ｕ{１，２，…，ＮＰ} ； Ｅｌｓｅ Ｉｆ ｒａｎｄ（）＜ＳＲＰ ／ ／ 自我学习方法调整 ｘ ｊ ｎｅｗ ＝ ｘ ｊ ｎｅｗ ±ｒａｎｄ(０，１) ∗Ｓｔｅｐ(ｊ) ； Ｅｌｓｅ Ｉｆ ｒａｎｄ（）＜ＩＬＰ ／ ／ 创新学习 ｘ ｊ ｎｅｗ ＝ Ｌ ｊ＋ｒａｎｄ（０，１）× Ｕ ｊ－Ｌ ｊ ( ) ； Ｅｌｓｅ ｘ ｊ ｎｅｗ ＝ ｘ ｊ ｉ Ｅｎｄ Ｘｎｅｗ ＝ （ｘ １ ｎｅｗ ，ｘ ２ ｎｅｗ ，…，ｘ ｄ ｎｅｗ ） Ｅｎｄ Ｅｎｄ 算法中，Ｓｔｅｐ 是自我学习调整步长，定义为 Ｓｔｅｐ ＝ ｍｉｎＳｔｅｐ ＋ （ｍａｘＳｔｅｐ － ｍｉｎＳｔｅｐ ）（１ － ｔ ／ Ｔｍａｘ）． 式中：ｍａｘＳｔｅｐ ＝ （Ｕ－Ｌ） ／ ５０，ｍｉｎＳｔｅｐ ＝ （Ｕ－Ｌ） ／ ３ ０００，ｔ 是当前迭代次数，Ｔ 是允许最大迭代次数． ３ 利用 ＭＴＬＢＯ 算法进行函数优化 ３．１ 多峰值函数 Ｓｃｈｗｅｆｅｌ２．２６ 测试分析 为了验证本文算法的性能，首先对一个经典的 高维多峰值函数 Ｓｃｈｗｅｆｅｌ ２．２６ 进行测试检验，将本 文算法与 ＧＡ 和基本的 ＴＬＢＯ 算法进行比较，设置 函数维数 ｄ ＝ １００， 种群大小 ＮＰ ＝ ５０，最大迭代次数 Ｔｍａｘ ＝ ５ ０００．遗传算法参数：交叉概率 ｃｐ ＝ ０．６，变异 概率 ｍｐ ＝ ０．１；本文算法参数：ＴｏＰ ＝ ０．５５，ＳＲＰ ＝ ０．３， ＩＬＰ ＝ ０．１．为了公平起见，每个算法独立运行 ３０ 次， 取其最优值，并统计其最佳解 Ｂｅｓｔ，最差解 Ｗｏｒｓｔ，平 第 ４ 期 拓守恒：一种优化神经网络的教与学优化算法 ·３２９·

·330· 智能系统学报 第8卷 均最优解Mean,标准差Std和算法运行时间Runt- 刻的方差平均值.通过跟踪记录种群在搜索空间的 ime,具体结果如表1所示.图1和图2分别给出3中 多样性变化，判断算法的空间探索能力.较好的优化 算法的优化过程曲线和30次独立运行最优解统计 算法前期具有较大的种群多样性，随着优化的进行， 盒图 种群逐步向全局最优点靠近，多样性逐步降低图3 表1算法GA、TLB0和MTLBO对函数Schwefel2.26的测 是在D=l00时.多峰值函数Schwefel2.26的种群多 试结果 样性变化曲线.从图3可以看出，本文算法的收敛曲 Table 1 The test results of three algorithms (GA,TLBO 线是在“活跃跳动”中逐步下降，使其能够获得高精度 and MTLBO)for function Schwefel 2.26 的全局最优解，而算法GA和TLBO算法的多样性很 参数 GA TLBO MTLBO 快就处于一种停滞状态，这是由于Schwefel2.26存在 Best 41507.39 16347.970 0.001590 很多函数值比较接近和相等的“局部”最优解，而全局 Mean 41503.93 25933.470 0.003708 最优解是在边界附近的点(420.9687,420.9687，…， Worst 41501.83 35622.770 0.007314 420.9687),在没有发现全局最优解时，个体是在各 Std 3.89908 5452.302 0.001547 个相近的局部最优解间跳动，使得搜索能力降低，全 运行时间/s 41.04843 12.779560 16.899730 局收敛性变差 3.010 43*10 ---TLBO---MTLBO—GA 2.5 4. 业Y%上恤 3.5 2.0叶 3.0 9ttt656纯的pp 燕1.5 2.5 2.0 1.0 -GA 1.5 -TLBO 0.5M 1.0 *一MTLBO 0.5 0.51.01.52.02.53.03.54.04.55.0 000132艺5节岁芳若搭芳ǒ10 迭代次数 迭代次数 图3种群多样性变化曲线 图13种算法平均优化过程曲线 Fig.3 The diversity curve of population Fig.1 The mean convergence curve of three algorithms 4.5r*10 基于MTLBO的BP神经网络优化 4.0h 本文目标是利用改进的教与学优化算法对神经 3.5 3.0 网络中的所有权值和阈值进行优化，使得网络的输 2.5 出值和期望输出值之间的误差尽可能的小、 2.0 盛 为了检验本文算法在神经网络优化中的性能， 1.5 1.0 分别通过函数拟合实验和拖拉机齿轮箱故障测试进 0.5 行验证.并且与遗传算法(GA)和基本TLBO算法进 行比较，算法的初始化参数设置如表2. GA TLBO MTLBO 图23种算法30次运行最优解统计盒 表2算法参数设置 Fig.2 The box diagram of optimal solution for three al- Table 2 Parameters setting of algorithms gorithms over 30 separate runs 最大评价次 3.2算法多样性与收敛性分析 算法 NP 其他参数 数(FEs) 为了验证本文算法的种群多样性变化和收敛 GA 50 cp=0.6,mp=0.1 性，利用下列公式跟踪记录种群的多样性变化 TLBO 50 20 ToP=0.55,SRP=0.3, MTLBO 50 su() LP=0.1 PV()=d 4.1 函数拟合 式中：Std,(t)表示在时刻t时，第i维上的标准差 本文选取函数Griewank:y(x)= 1 PV(t)(population variance,PV)表示所有维在t时 4000台

均最优解 Ｍｅａｎ，标准差 Ｓｔｄ 和算法运行时间 Ｒｕｎｔ⁃ ｉｍｅ，具体结果如表 １ 所示．图 １ 和图 ２ 分别给出 ３ 中 算法的优化过程曲线和 ３０ 次独立运行最优解统计 盒图． 表 １ 算法 ＧＡ、ＴＬＢＯ 和 ＭＴＬＢＯ 对函数 Ｓｃｈｗｅｆｅｌ ２．２６ 的测 试结果 Ｔａｂｌｅ １ Ｔｈｅ ｔｅｓｔ ｒｅｓｕｌｔｓ ｏｆ ｔｈｒｅｅ ａｌｇｏｒｉｔｈｍｓ （ＧＡ， ＴＬＢＯ ａｎｄ ＭＴＬＢＯ） ｆｏｒ ｆｕｎｃｔｉｏｎ Ｓｃｈｗｅｆｅｌ ２．２６ 参数 ＧＡ ＴＬＢＯ ＭＴＬＢＯ Ｂｅｓｔ ４１ ５０７．３９ １６ ３４７．９７０ ０．００１ ５９０ Ｍｅａｎ ４１ ５０３．９３ ２５ ９３３．４７０ ０．００３ ７０８ Ｗｏｒｓｔ ４１ ５０１．８３ ３５ ６２２．７７０ ０．００７ ３１４ Ｓｔｄ ３．８９９ ０８ ５ ４５２．３０２ ０．００１ ５４７ 运行时间／ ｓ ４１．０４８ ４３ １２．７７９ ５６０ １６．８９９ ７３０ 图 １ ３ 种算法平均优化过程曲线 Ｆｉｇ．１ Ｔｈｅ ｍｅａｎ ｃｏｎｖｅｒｇｅｎｃｅ ｃｕｒｖｅ ｏｆ ｔｈｒｅｅ ａｌｇｏｒｉｔｈｍｓ 图 ２ ３ 种算法 ３０ 次运行最优解统计盒 Ｆｉｇ．２ Ｔｈｅ ｂｏｘ ｄｉａｇｒａｍ ｏｆ ｏｐｔｉｍａｌ ｓｏｌｕｔｉｏｎ ｆｏｒ ｔｈｒｅｅ ａｌ⁃ ｇｏｒｉｔｈｍｓ ｏｖｅｒ ３０ ｓｅｐａｒａｔｅ ｒｕｎｓ ３．２ 算法多样性与收敛性分析 为了验证本文算法的种群多样性变化和收敛 性，利用下列公式跟踪记录种群的多样性变化． ＰＶ（ｔ） ＝ １ ｄ ∑ ｄ ｉ ＝ １ Ｓｔｄｉ（ｔ）． 式中：Ｓｔｄｉ（ｔ） 表示在时刻 ｔ 时，第 ｉ 维上的标准差． ＰＶ（ｔ） （ｐｏｐｕｌａｔｉｏｎ ｖａｒｉａｎｃｅ， ＰＶ）表示所有维在 ｔ 时 刻的方差平均值．通过跟踪记录种群在搜索空间的 多样性变化，判断算法的空间探索能力．较好的优化 算法前期具有较大的种群多样性，随着优化的进行， 种群逐步向全局最优点靠近，多样性逐步降低．图 ３ 是在 Ｄ＝ １００ 时，多峰值函数 Ｓｃｈｗｅｆｅｌ ２．２６ 的种群多 样性变化曲线．从图 ３ 可以看出，本文算法的收敛曲 线是在“活跃跳动”中逐步下降，使其能够获得高精度 的全局最优解，而算法 ＧＡ 和 ＴＬＢＯ 算法的多样性很 快就处于一种停滞状态，这是由于 Ｓｃｈｗｅｆｅｌ ２．２６ 存在 很多函数值比较接近和相等的“局部”最优解，而全局 最优解是在边界附近的点（４２０．９６８ ７，４２０．９６８ ７，…， ４２０．９６８ ７）， 在没有发现全局最优解时，个体是在各 个相近的局部最优解间跳动，使得搜索能力降低，全 局收敛性变差． 图 ３ 种群多样性变化曲线 Ｆｉｇ．３ Ｔｈｅ ｄｉｖｅｒｓｉｔｙ ｃｕｒｖｅ ｏｆ ｐｏｐｕｌａｔｉｏｎ ４ 基于 ＭＴＬＢＯ 的 ＢＰ 神经网络优化 本文目标是利用改进的教与学优化算法对神经 网络中的所有权值和阈值进行优化，使得网络的输 出值和期望输出值之间的误差尽可能的小． 为了检验本文算法在神经网络优化中的性能， 分别通过函数拟合实验和拖拉机齿轮箱故障测试进 行验证．并且与遗传算法（ＧＡ）和基本 ＴＬＢＯ 算法进 行比较，算法的初始化参数设置如表 ２． 表 ２ 算法参数设置 Ｔａｂｌｅ ２ Ｐａｒａｍｅｔｅｒｓ ｓｅｔｔｉｎｇ ｏｆ ａｌｇｏｒｉｔｈｍｓ 算法 最大评价次 数（ＦＥｓ） ＮＰ 其他参数 ＧＡ ５０ — ｃｐ ＝ ０．６， ｍｐ ＝ ０．１ ＴＬＢＯ ５０ ２０ ＭＴＬＢＯ ５０ — ＴｏＰ ＝ ０．５５，ＳＲＰ ＝ ０．３， ＩＬＰ ＝ ０．１ ４．１ 函数拟合 本文选取函数 Ｇｒｉｅｗａｎｋ： ｙ （ ｘ） ＝ １ ４ ０００ ∑ ｄ ｉ ＝ １ ｘ ２ ｉ － ·３３０· 智 能 系 统 学 报 第 ８ 卷

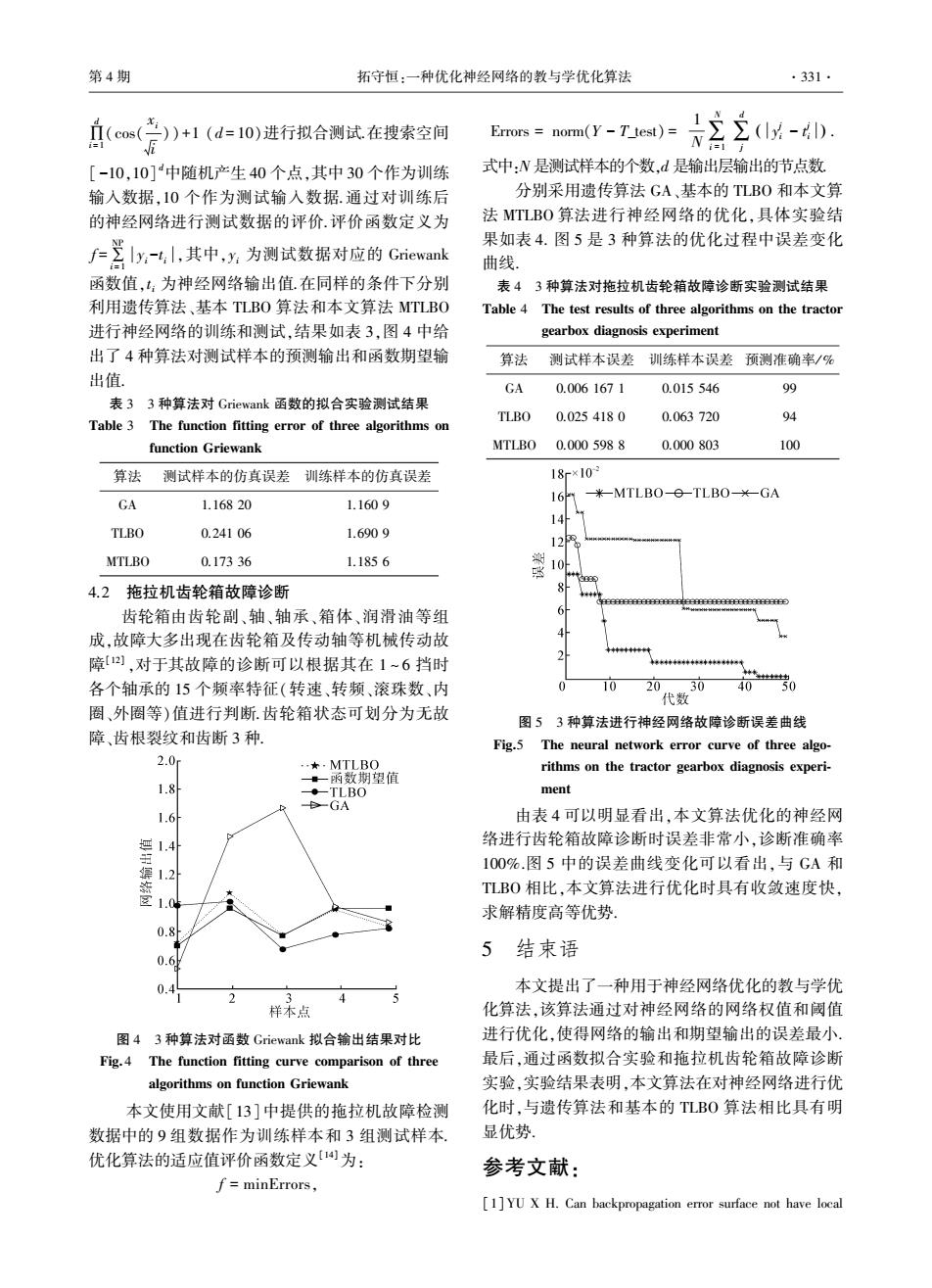
第4期 拓守恒：一种优化神经网络的教与学优化算法 .331· (cos(点)+1(d=10)进行拟合测试在搜素空间 Errors norm(Y-T_test)= [-10,10]中随机产生40个点，其中30个作为训练 式中：N是测试样本的个数，d是输出层输出的节点数 输入数据，10个作为测试输入数据.通过对训练后 分别采用遗传算法GA、基本的TLBO和本文算 的神经网络进行测试数据的评价.评价函数定义为 法MTLBO算法进行神经网络的优化，具体实验结 户三引x-4,其中，x为测试数据对应的Grievan止 果如表4.图5是3种算法的优化过程中误差变化 曲线 函数值，t:为神经网络输出值.在同样的条件下分别 表43种算法对拖拉机齿轮箱故障诊断实验测试结果 利用遗传算法、基本TLBO算法和本文算法MTLBO Table 4 The test results of three algorithms on the tractor 进行神经网络的训练和测试，结果如表3，图4中给 gearbox diagnosis experiment 出了4种算法对测试样本的预测输出和函数期望输 算法 测试样本误差训练样本误差预测准确率/% 出值. GA 0.0061671 0.015546 99 表33种算法对Griewank函数的拟合实验测试结果 TLBO 0.0254180 0.063720 94 Table 3 The function fitting error of three algorithms on function Griewank MTLB00.0005988 0.000803 100 算法 测试样本的仿真误差训练样本的仿真误差 18r×10 米-MTLBO--TLBO--GA GA 1.16820 1.1609 16 14 TLBO 0.24106 1.6909 12 MTLBO 0.17336 1.1856 10 4.2拖拉机齿轮箱故障诊断 齿轮箱由齿轮副、轴、轴承、箱体、润滑油等组 成，故障大多出现在齿轮箱及传动轴等机械传动故 障四)，对于其故障的诊断可以根据其在1~6挡时 各个轴承的15个频率特征（转速、转频、滚珠数、内 1020 30 0 40 代数 圈、外圈等)值进行判断.齿轮箱状态可划分为无故 图53种算法进行神经网络故障诊断误差曲线 障、齿根裂纹和齿断3种 Fig.5 The neural network error curve of three algo- 2.0m ,★，MTLBO rithms on the tractor gearbox diagnosis experi- 一。一函数期望值 1.8 ·-TLBO ment BGA 1.6 由表4可以明显看出，本文算法优化的神经网 络进行齿轮箱故障诊断时误差非常小，诊断准确率 鏢 100%.图5中的误差曲线变化可以看出，与GA和 1.2 TLB0相比，本文算法进行优化时具有收敛速度快， 求解精度高等优势 0.8 5结束语 0.6 0.4 本文提出了一种用于神经网络优化的教与学优 c3 样本点 化算法，该算法通过对神经网络的网络权值和阈值 图43种算法对函数Griewank拟合输出结果对比 进行优化，使得网络的输出和期望输出的误差最小 Fig.4 The function fitting curve comparison of three 最后，通过函数拟合实验和拖拉机齿轮箱故障诊断 algorithms on function Griewank 实验，实验结果表明，本文算法在对神经网络进行优 本文使用文献[13]中提供的拖拉机故障检测 化时，与遗传算法和基本的TLB0算法相比具有明 数据中的9组数据作为训练样本和3组测试样本 显优势 优化算法的适应值评价函数定义[为： 参考文献： f=minErrors, [1]YU X H.Can backpropagation error surface not have local

∏ ｄ ｉ ＝ １ （ｃｏｓ（ ｘｉ ｉ ））＋１ （ｄ ＝ １０）进行拟合测试．在搜索空间 ［ －１０，１０］ ｄ中随机产生 ４０ 个点，其中 ３０ 个作为训练 输入数据，１０ 个作为测试输入数据．通过对训练后 的神经网络进行测试数据的评价．评价函数定义为 ｆ ＝∑ ＮＰ ｉ ＝ １ ｙｉ －ｔ ｉ ，其中，ｙｉ 为测试数据对应的 Ｇｒｉｅｗａｎｋ 函数值，ｔ ｉ 为神经网络输出值．在同样的条件下分别 利用遗传算法、基本 ＴＬＢＯ 算法和本文算法 ＭＴＬＢＯ 进行神经网络的训练和测试，结果如表 ３，图 ４ 中给 出了 ４ 种算法对测试样本的预测输出和函数期望输 出值． 表 ３ ３ 种算法对 Ｇｒｉｅｗａｎｋ 函数的拟合实验测试结果 Ｔａｂｌｅ ３ Ｔｈｅ ｆｕｎｃｔｉｏｎ ｆｉｔｔｉｎｇ ｅｒｒｏｒ ｏｆ ｔｈｒｅｅ ａｌｇｏｒｉｔｈｍｓ ｏｎ ｆｕｎｃｔｉｏｎ Ｇｒｉｅｗａｎｋ 算法 测试样本的仿真误差 训练样本的仿真误差 ＧＡ １．１６８ ２０ １．１６０ ９ ＴＬＢＯ ０．２４１ ０６ １．６９０ ９ ＭＴＬＢＯ ０．１７３ ３６ １．１８５ ６ ４．２ 拖拉机齿轮箱故障诊断 齿轮箱由齿轮副、轴、轴承、箱体、润滑油等组 成，故障大多出现在齿轮箱及传动轴等机械传动故 障［１２］ ，对于其故障的诊断可以根据其在 １ ～ ６ 挡时 各个轴承的 １５ 个频率特征（转速、转频、滚珠数、内 圈、外圈等）值进行判断．齿轮箱状态可划分为无故 障、齿根裂纹和齿断 ３ 种． 图 ４ ３ 种算法对函数 Ｇｒｉｅｗａｎｋ 拟合输出结果对比 Ｆｉｇ． ４ Ｔｈｅ ｆｕｎｃｔｉｏｎ ｆｉｔｔｉｎｇ ｃｕｒｖｅ ｃｏｍｐａｒｉｓｏｎ ｏｆ ｔｈｒｅｅ ａｌｇｏｒｉｔｈｍｓ ｏｎ ｆｕｎｃｔｉｏｎ Ｇｒｉｅｗａｎｋ 本文使用文献［１３］中提供的拖拉机故障检测 数据中的 ９ 组数据作为训练样本和 ３ 组测试样本． 优化算法的适应值评价函数定义［１４］为： ｆ ＝ ｍｉｎＥｒｒｏｒｓ， Ｅｒｒｏｒｓ ＝ ｎｏｒｍ（Ｙ － Ｔ＿ｔｅｓｔ） ＝ １ Ｎ∑ Ｎ ｉ ＝ １ ∑ ｄ ｊ ｙ ｊ ｉ － ｔ ｊ ｉ ( ) ． 式中：Ｎ 是测试样本的个数，ｄ 是输出层输出的节点数． 分别采用遗传算法 ＧＡ、基本的 ＴＬＢＯ 和本文算 法 ＭＴＬＢＯ 算法进行神经网络的优化，具体实验结 果如表 ４． 图 ５ 是 ３ 种算法的优化过程中误差变化 曲线． 表 ４ ３ 种算法对拖拉机齿轮箱故障诊断实验测试结果 Ｔａｂｌｅ ４ Ｔｈｅ ｔｅｓｔ ｒｅｓｕｌｔｓ ｏｆ ｔｈｒｅｅ ａｌｇｏｒｉｔｈｍｓ ｏｎ ｔｈｅ ｔｒａｃｔｏｒ ｇｅａｒｂｏｘ ｄｉａｇｎｏｓｉｓ ｅｘｐｅｒｉｍｅｎｔ 算法 测试样本误差 训练样本误差 预测准确率／ ％ ＧＡ ０．００６ １６７ １ ０．０１５ ５４６ ９９ ＴＬＢＯ ０．０２５ ４１８ ０ ０．０６３ ７２０ ９４ ＭＴＬＢＯ ０．０００ ５９８ ８ ０．０００ ８０３ １００ 图 ５ ３ 种算法进行神经网络故障诊断误差曲线 Ｆｉｇ．５ Ｔｈｅ ｎｅｕｒａｌ ｎｅｔｗｏｒｋ ｅｒｒｏｒ ｃｕｒｖｅ ｏｆ ｔｈｒｅｅ ａｌｇｏ⁃ ｒｉｔｈｍｓ ｏｎ ｔｈｅ ｔｒａｃｔｏｒ ｇｅａｒｂｏｘ ｄｉａｇｎｏｓｉｓ ｅｘｐｅｒｉ⁃ ｍｅｎｔ 由表 ４ 可以明显看出，本文算法优化的神经网 络进行齿轮箱故障诊断时误差非常小，诊断准确率 １００％．图 ５ 中的误差曲线变化可以看出，与 ＧＡ 和 ＴＬＢＯ 相比，本文算法进行优化时具有收敛速度快， 求解精度高等优势． ５ 结束语 本文提出了一种用于神经网络优化的教与学优 化算法，该算法通过对神经网络的网络权值和阈值 进行优化，使得网络的输出和期望输出的误差最小． 最后，通过函数拟合实验和拖拉机齿轮箱故障诊断 实验，实验结果表明，本文算法在对神经网络进行优 化时，与遗传算法和基本的 ＴＬＢＯ 算法相比具有明 显优势． 参考文献： ［１］ＹＵ Ｘ Ｈ． Ｃａｎ ｂａｃｋｐｒｏｐａｇａｔｉｏｎ ｅｒｒｏｒ ｓｕｒｆａｃｅ ｎｏｔ ｈａｖｅ ｌｏｃａｌ 第 ４ 期 拓守恒：一种优化神经网络的教与学优化算法 ·３３１·

.332. 智能系统学报 第8卷 minims[J].Neural Networks,1992,3(6):1009-1021. [10]GEEM Z W,KIM J H,LOGANATHAN G V.A new heu- [2]YU X H,CHEN G A.On the local minima free condition of ristic optimization algorithm:harmony search[J].Simula- backpropagation learning[J].IEEE Transactions on Neural tiom,2001,76(2):60-68. Networks,1995,6(5):1300-1303. [11]TUO Shouheng,YONG Longquan.An improved harmony [3]GOLDBERG D E,KORB B.DEB K.Messy genetic algo- search algorithm with chaos[].Joural of Computational rithms:motivation,analysis,and first results[J.Complex Information Systems,2012,8(10):4269-4276. Systems,1989,3(5):493-530. [12]赵爽.基于SVM的拖拉机齿轮箱多故障诊断方法研究 [4]CLERC M,KENNEDY J.The particle swarm-explosion, [J刀.农机化研究，2011,33(5)：207-209. stability,and convergence in a multidimensional complex ZHAO Shuang.Research of multi-faults in the Tractor's space[J].IEEE Transactions on Evolutionary Computation, gearbox based on support vector machines method [J]. 2002,6(1):58-73. Journal of Agricultural Mechanization Research,2011,33 [5]RAO R V,SAVSANI V J,VAKHARIA D P.Teaching- (5):207-209. learning-based optimization:a novel method for constrained [l3]史峰，王辉，胡斐，等.Matlab智能算法30个案例分析 mechanical design optimization problems[].Computer Ai- [M].北京：北京航空航天大学出版社，2011：137- ded Design,2011,43(3):303-315. 144. [6]RAO R V,SAVSANI V J,VAKHARIA D P.Teaching- [14]杜文莉，周仁，赵亮，等.基于量子差分进化算法的神经 learning-based optimization:an optimization method for 网络优化方法[J].清华大学学报：自然科学，2012,52 continuous non-linear large scale problems[].Information (3):331-335. Sciences,2012,183(1):1-15. DU Wenli,ZHOU Ren,ZHAO Liang,et al.Cooperative [7]MATEJ C.LIU S H,MERNIK L.A note on teaching-learn- quantum differential evolution algorithm based method for ing-based optimization algorithm[].Information Sciences, optimizing neural networks[J].Journal of Tsinghua Univer- 2012,212(1):79-93. sity:Science and Technology,2012,52(3):331-335. [8]RAO R V,PATEL V.An elitist teaching-learning-based op- 作者简介： timization algorithm for solving complex constrained optimi- 拓守恒，男，1978年生，讲师，CCF zation problems[J.International Journal of Industrial Engi- 会员，主要研究方向为智能优化算法与 neering Computations,2012,3(4):535-560. 智能信息处理，发表学术论文多篇 [9]ZOU D X.GAO L Q,WU J H,et al.A novel global har- mony search algorithm for reliability problems[].Comput- ers and Industrial Engineering,2010,58(2):307-316

ｍｉｎｉｍｓ［Ｊ］． Ｎｅｕｒａｌ Ｎｅｔｗｏｒｋｓ， １９９２， ３（６）： １００９⁃１０２１． ［２］ＹＵ Ｘ Ｈ， ＣＨＥＮ Ｇ Ａ． Ｏｎ ｔｈｅ ｌｏｃａｌ ｍｉｎｉｍａ ｆｒｅｅ ｃｏｎｄｉｔｉｏｎ ｏｆ ｂａｃｋｐｒｏｐａｇａｔｉｏｎ ｌｅａｒｎｉｎｇ［ Ｊ］． ＩＥＥＥ Ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ Ｎｅｕｒａｌ Ｎｅｔｗｏｒｋｓ， １９９５， ６（５）： １３００⁃１３０３． ［３］ＧＯＬＤＢＥＲＧ Ｄ Ｅ， ＫＯＲＢ Ｂ， ＤＥＢ Ｋ． Ｍｅｓｓｙ ｇｅｎｅｔｉｃ ａｌｇｏ⁃ ｒｉｔｈｍｓ： ｍｏｔｉｖａｔｉｏｎ， ａｎａｌｙｓｉｓ， ａｎｄ ｆｉｒｓｔ ｒｅｓｕｌｔｓ［Ｊ］． Ｃｏｍｐｌｅｘ Ｓｙｓｔｅｍｓ， １９８９， ３（５）： ４９３⁃５３０． ［４］ＣＬＥＲＣ Ｍ， ＫＥＮＮＥＤＹ Ｊ． Ｔｈｅ ｐａｒｔｉｃｌｅ ｓｗａｒｍ—ｅｘｐｌｏｓｉｏｎ， ｓｔａｂｉｌｉｔｙ， ａｎｄ ｃｏｎｖｅｒｇｅｎｃｅ ｉｎ ａ ｍｕｌｔｉｄｉｍｅｎｓｉｏｎａｌ ｃｏｍｐｌｅｘ ｓｐａｃｅ［Ｊ］． ＩＥＥＥ Ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ Ｅｖｏｌｕｔｉｏｎａｒｙ Ｃｏｍｐｕｔａｔｉｏｎ， ２００２， ６ （１）： ５８⁃７３． ［５］ ＲＡＯ Ｒ Ｖ， ＳＡＶＳＡＮＩ Ｖ Ｊ， ＶＡＫＨＡＲＩＡ Ｄ Ｐ． Ｔｅａｃｈｉｎｇ⁃ ｌｅａｒｎｉｎｇ⁃ｂａｓｅｄ ｏｐｔｉｍｉｚａｔｉｏｎ： ａ ｎｏｖｅｌ ｍｅｔｈｏｄ ｆｏｒ ｃｏｎｓｔｒａｉｎｅｄ ｍｅｃｈａｎｉｃａｌ ｄｅｓｉｇｎ ｏｐｔｉｍｉｚａｔｉｏｎ ｐｒｏｂｌｅｍｓ［Ｊ］． Ｃｏｍｐｕｔｅｒ Ａｉ⁃ ｄｅｄ Ｄｅｓｉｇｎ， ２０１１， ４３（３）： ３０３⁃３１５． ［６］ ＲＡＯ Ｒ Ｖ， ＳＡＶＳＡＮＩ Ｖ Ｊ， ＶＡＫＨＡＲＩＡ Ｄ Ｐ． Ｔｅａｃｈｉｎｇ⁃ ｌｅａｒｎｉｎｇ⁃ｂａｓｅｄ ｏｐｔｉｍｉｚａｔｉｏｎ： ａｎ ｏｐｔｉｍｉｚａｔｉｏｎ ｍｅｔｈｏｄ ｆｏｒ ｃｏｎｔｉｎｕｏｕｓ ｎｏｎ⁃ｌｉｎｅａｒ ｌａｒｇｅ ｓｃａｌｅ ｐｒｏｂｌｅｍｓ［ Ｊ］． Ｉｎｆｏｒｍａｔｉｏｎ Ｓｃｉｅｎｃｅｓ， ２０１２， １８３ （１）： １⁃１５． ［７］ＭＡＴＥＪ Ｃ， ＬＩＵ Ｓ Ｈ， ＭＥＲＮＩＫ Ｌ． Ａ ｎｏｔｅ ｏｎ ｔｅａｃｈｉｎｇ⁃ｌｅａｒｎ⁃ ｉｎｇ⁃ｂａｓｅｄ ｏｐｔｉｍｉｚａｔｉｏｎ ａｌｇｏｒｉｔｈｍ［ Ｊ］． Ｉｎｆｏｒｍａｔｉｏｎ Ｓｃｉｅｎｃｅｓ， ２０１２， ２１２ （１）： ７９⁃９３． ［８］ＲＡＯ Ｒ Ｖ， ＰＡＴＥＬ Ｖ． Ａｎ ｅｌｉｔｉｓｔ ｔｅａｃｈｉｎｇ⁃ｌｅａｒｎｉｎｇ⁃ｂａｓｅｄ ｏｐ⁃ ｔｉｍｉｚａｔｉｏｎ ａｌｇｏｒｉｔｈｍ ｆｏｒ ｓｏｌｖｉｎｇ ｃｏｍｐｌｅｘ ｃｏｎｓｔｒａｉｎｅｄ ｏｐｔｉｍｉ⁃ ｚａｔｉｏｎ ｐｒｏｂｌｅｍｓ［Ｊ］． Ｉｎｔｅｒｎａｔｉｏｎａｌ Ｊｏｕｒｎａｌ ｏｆ Ｉｎｄｕｓｔｒｉａｌ Ｅｎｇｉ⁃ ｎｅｅｒｉｎｇ Ｃｏｍｐｕｔａｔｉｏｎｓ， ２０１２， ３（４）： ５３５⁃５６０． ［９］ＺＯＵ Ｄ Ｘ， ＧＡＯ Ｌ Ｑ， ＷＵ Ｊ Ｈ， ｅｔ ａｌ． Ａ ｎｏｖｅｌ ｇｌｏｂａｌ ｈａｒ⁃ ｍｏｎｙ ｓｅａｒｃｈ ａｌｇｏｒｉｔｈｍ ｆｏｒ ｒｅｌｉａｂｉｌｉｔｙ ｐｒｏｂｌｅｍｓ［ Ｊ］． Ｃｏｍｐｕｔ⁃ ｅｒｓ ａｎｄ Ｉｎｄｕｓｔｒｉａｌ Ｅｎｇｉｎｅｅｒｉｎｇ， ２０１０， ５８ （２）： ３０７⁃３１６． ［１０］ＧＥＥＭ Ｚ Ｗ， ＫＩＭ Ｊ Ｈ， ＬＯＧＡＮＡＴＨＡＮ Ｇ Ｖ． Ａ ｎｅｗ ｈｅｕ⁃ ｒｉｓｔｉｃ ｏｐｔｉｍｉｚａｔｉｏｎ ａｌｇｏｒｉｔｈｍ： ｈａｒｍｏｎｙ ｓｅａｒｃｈ［ Ｊ］． Ｓｉｍｕｌａ⁃ ｔｉｏｎ， ２００１， ７６（２）： ６０⁃６８． ［１１］ ＴＵＯ Ｓｈｏｕｈｅｎｇ， ＹＯＮＧ Ｌｏｎｇｑｕａｎ． Ａｎ ｉｍｐｒｏｖｅｄ ｈａｒｍｏｎｙ ｓｅａｒｃｈ ａｌｇｏｒｉｔｈｍ ｗｉｔｈ ｃｈａｏｓ［ Ｊ］． Ｊｏｕｒｎａｌ ｏｆ Ｃｏｍｐｕｔａｔｉｏｎａｌ Ｉｎｆｏｒｍａｔｉｏｎ Ｓｙｓｔｅｍｓ， ２０１２， ８（１０）： ４２６９⁃４２７６． ［１２］赵爽． 基于 ＳＶＭ 的拖拉机齿轮箱多故障诊断方法研究 ［Ｊ］． 农机化研究， ２０１１， ３３（５）： ２０７⁃２０９． ＺＨＡＯ Ｓｈｕａｎｇ． Ｒｅｓｅａｒｃｈ ｏｆ ｍｕｌｔｉ⁃ｆａｕｌｔｓ ｉｎ ｔｈｅ Ｔｒａｃｔｏｒ’ ｓ ｇｅａｒｂｏｘ ｂａｓｅｄ ｏｎ ｓｕｐｐｏｒｔ ｖｅｃｔｏｒ ｍａｃｈｉｎｅｓ ｍｅｔｈｏｄ ［ Ｊ ］． Ｊｏｕｒｎａｌ ｏｆ Ａｇｒｉｃｕｌｔｕｒａｌ Ｍｅｃｈａｎｉｚａｔｉｏｎ Ｒｅｓｅａｒｃｈ， ２０１１， ３３ （５）： ２０７⁃２０９． ［１３］史峰，王辉，胡斐，等． Ｍａｔｌａｂ 智能算法 ３０ 个案例分析 ［Ｍ］． 北京： 北京航空航天大学出版社， ２０１１： １３７⁃ １４４． ［１４］杜文莉，周仁，赵亮，等． 基于量子差分进化算法的神经 网络优化方法［Ｊ］． 清华大学学报：自然科学， ２０１２， ５２ （３）： ３３１⁃３３５． ＤＵ Ｗｅｎｌｉ， ＺＨＯＵ Ｒｅｎ， ＺＨＡＯ Ｌｉａｎｇ， ｅｔ ａｌ． Ｃｏｏｐｅｒａｔｉｖｅ ｑｕａｎｔｕｍ ｄｉｆｆｅｒｅｎｔｉａｌ ｅｖｏｌｕｔｉｏｎ ａｌｇｏｒｉｔｈｍ ｂａｓｅｄ ｍｅｔｈｏｄ ｆｏｒ ｏｐｔｉｍｉｚｉｎｇ ｎｅｕｒａｌ ｎｅｔｗｏｒｋｓ［Ｊ］．Ｊｏｕｒｎａｌ ｏｆ Ｔｓｉｎｇｈｕａ Ｕｎｉｖｅｒ⁃ ｓｉｔｙ： Ｓｃｉｅｎｃｅ ａｎｄ Ｔｅｃｈｎｏｌｏｇｙ， ２０１２， ５２（３）： ３３１⁃３３５． 作者简介： 拓守恒，男，１９７８ 年生，讲师，ＣＣＦ 会员，主要研究方向为智能优化算法与 智能信息处理，发表学术论文多篇． ·３３２· 智 能 系 统 学 报 第 ８ 卷