
第8卷第3期 智能系统学报 Vol.8 No.3 2013年6月 CAAI Transactions on Intelligent Systems Jun.2013 D0I:10.3969/i.issn.1673-4785.201211047 网络出版地址:http://www.cnki.net/kcms/detail/23.1538.TP.20130125.1436.003.html 具有Lévy飞行特征的蝙蝠算法 刘长平12,叶春明 (1.上海理工大学管理学院,上海200093:2.淮阴工学院经济管理学院,江苏淮安223001) 摘要:针对基本蝙蝠算法易早熟、收敛精度低等不足,在分析蝙蝠算法优化机理和局限性的基础上,从算法仿生原 理入手,采用Ly飞行搜索策略更为真实地模拟蝙蝠的捕食行为,取代原有算法的速度和位置更新方式,充分利用 Ly飞行会产生较大跳跃这种不均匀随机游走的特性,有效避免局部极值的吸引通过标准测试函数对所提算法进 行仿真测试,结果表明所提算法有效克服了原算法易早熟、收敛精度低等缺陷,在寻优精度和全局收敛性能方面明 显优于基本蝙蝠算法和粒子群优化算法,是解决复杂函数优化问题的一种有效工具 关键词:蝙蝠算法;Léy飞行;函数优化;粒子群优化算法 中图分类号:TP301.6:N945文献标志码:A文章编号:1673-4785(2013)03-0240-07 中文引用格式:刘长平,叶春明.具有Ly飞行特征的蝙蝠算法[J].智能系统学报,2013,8(3):240-246. 英文引用格式:LIU Changping,.YE Chunming.Bat algorithm with the characteristics of Levy flights[J].CAAI Transactions on In- telligent Systems.2013,8(3):240-246. Bat algorithm with the characteristics of Levy flights LIU Changping'.2,YE Chunming' (1.College of Management,University of Shanghai for Science Technology,Shanghai 200093,China;2.College of Economics Management,Huaiyin Institute of Technology,Huaian 223001,China) Abstract:The basic bat algorithm (BA)in the past research studies reveal deficiencies as apt to be premature and low precision of convergence.This paper first analyzed the optimization mechanism and deficiency of bat algorithm (BA),and then considering the Levy flight behaviors of bats can simulate predatory more realistically,the study proposed substituting for the speed and location updating pattern of former algorithm.The proposed algorithm fully explored the trait of uneven random walks,so that clusters of short steps were connected by rare long steps,to a- void being trapped in local optimal solution.Simulation results for benchmark functions show that the proposed algo- rithm improved the global optimization ability remarkably and outperformed the basic BA and particle swarm optimi- zation (PSO)in accuracy and convergence property.Therefore,the proposed algorithm is an effective tool for sol- ving the optimization of complex functions. Keywords:bat algorithm;Levy flight;function optimization;particle swarm optimization 相对于传统优化方法,群智能算法在优化过程用.近年来,受自然规律和生物群体智能行为的启 中仅需要目标函数的信息,不受搜索空间连续或可 发,一些新颖的仿生群智能算法如人工鱼群算 微的限制,能够以较大概率找到最优解或近似最优 法口、蜂群算法[2】、萤火虫算法[34等相继被提出, 解,并且具有操作简单、适宜并行计算、鲁棒性强等 显示出独特的特点和效果 特点,在科学计算和工程技术领域内得到了广泛应 蝙蝠是自然界中惟一会飞的一类哺乳动物,拥 有令人惊异的回声定位能力,通过探测发出的超声 收稿日期:2012-11-27.网络出版日期:2013-01-25. 波回波的时间延迟,利用回波到达双耳的时间差、回 基金项目:国家自然科学基金资助项目(71271138):教育部人文社会 科学规划基金资助项目(10Y门A630187);上海市教委科研 波音强的变化建立起周围环境的三维场景,蝙蝠不 创新重点资助项目(12ZS133):教育部高校博士学科点专 项科研基金资助项目(20093120110008). 仅能精确探测猎物的距离,还能识别其体型特征、方 通信作者:刘长平.E-mail:lcp_mail@163.com. 位和角度通过模拟蝙蝠借助超声波搜索、捕食猎物
第 8 卷第 3 期 智 能 系 统 学 报 Vol.8 №.3 2013 年 6 月 CAAI Transactions on Intelligent Systems Jun. 2013 DOI:10.3969 / j.issn.1673⁃4785.201211047 网络出版地址:http: / / www.cnki.net / kcms/ detail / 23.1538.TP.20130125.1436.003.html 具有 Lévy 飞行特征的蝙蝠算法 刘长平1,2 ,叶春明1 (1.上海理工大学 管理学院,上海 200093; 2.淮阴工学院 经济管理学院,江苏 淮安 223001) 摘 要:针对基本蝙蝠算法易早熟、收敛精度低等不足,在分析蝙蝠算法优化机理和局限性的基础上,从算法仿生原 理入手,采用 Lévy 飞行搜索策略更为真实地模拟蝙蝠的捕食行为,取代原有算法的速度和位置更新方式,充分利用 Lévy 飞行会产生较大跳跃这种不均匀随机游走的特性,有效避免局部极值的吸引.通过标准测试函数对所提算法进 行仿真测试,结果表明所提算法有效克服了原算法易早熟、收敛精度低等缺陷,在寻优精度和全局收敛性能方面明 显优于基本蝙蝠算法和粒子群优化算法,是解决复杂函数优化问题的一种有效工具. 关键词:蝙蝠算法;Lévy 飞行;函数优化;粒子群优化算法 中图分类号: TP301.6;N945 文献标志码:A 文章编号:1673⁃4785(2013)03⁃0240⁃07 中文引用格式:刘长平,叶春明.具有 Lévy 飞行特征的蝙蝠算法[J].智能系统学报, 2013, 8(3): 240⁃246. 英文引用格式:LIU Changping, YE Chunming. Bat algorithm with the characteristics of Lévy flights[J]. CAAI Transactions on In⁃ telligent Systems, 2013, 8(3): 240⁃246. Bat algorithm with the characteristics of Lévy flights LIU Changping 1,2 , YE Chunming 1 (1. College of Management, University of Shanghai for Science & Technology, Shanghai 200093, China; 2. College of Economics & Management, Huaiyin Institute of Technology, Huaian 223001, China) Abstract:The basic bat algorithm (BA) in the past research studies reveal deficiencies as apt to be premature and low precision of convergence. This paper first analyzed the optimization mechanism and deficiency of bat algorithm (BA), and then considering the Lévy flight behaviors of bats can simulate predatory more realistically, the study proposed substituting for the speed and location updating pattern of former algorithm. The proposed algorithm fully explored the trait of uneven random walks, so that clusters of short steps were connected by rare long steps, to a⁃ void being trapped in local optimal solution. Simulation results for benchmark functions show that the proposed algo⁃ rithm improved the global optimization ability remarkably and outperformed the basic BA and particle swarm optimi⁃ zation (PSO) in accuracy and convergence property. Therefore, the proposed algorithm is an effective tool for sol⁃ ving the optimization of complex functions. Keywords:bat algorithm; Lévy flight; function optimization; particle swarm optimization 收稿日期:2012⁃11⁃27. 网络出版日期:2013⁃01⁃25. 基金项目:国家自然科学基金资助项目(71271138);教育部人文社会 科学规划基金资助项目( 10YJA630187);上海市教委科研 创新重点资助项目(12ZS133);教育部高校博士学科点专 项科研基金资助项目(20093120110008). 通信作者:刘长平.E⁃mail:lcp_mail@ 163.com. 相对于传统优化方法,群智能算法在优化过程 中仅需要目标函数的信息,不受搜索空间连续或可 微的限制,能够以较大概率找到最优解或近似最优 解,并且具有操作简单、适宜并行计算、鲁棒性强等 特点,在科学计算和工程技术领域内得到了广泛应 用.近年来,受自然规律和生物群体智能行为的启 发,一些 新 颖 的 仿 生 群 智 能 算 法 如 人 工 鱼 群 算 法[1] 、蜂群算法[2] 、萤火虫算法[3⁃4] 等相继被提出, 显示出独特的特点和效果. 蝙蝠是自然界中惟一会飞的一类哺乳动物,拥 有令人惊异的回声定位能力,通过探测发出的超声 波回波的时间延迟,利用回波到达双耳的时间差、回 波音强的变化建立起周围环境的三维场景,蝙蝠不 仅能精确探测猎物的距离,还能识别其体型特征、方 位和角度.通过模拟蝙蝠借助超声波搜索、捕食猎物

第3期 刘长平,等:具有Ly飞行特征的蝙蝠算法 ·241· 的生物学特性,Yang曾提出一种基于随机优化的蝙 基于群体进化的算法,首先在可行解空间随机初始 蝠算法[),该算法具有模型简单、收敛速度快、可并 化种群,即确定个体的初始位置和初始速度,其中位 行处理等特点,在工程设计中得到了初步应用 置用于表征问题解;进而通过评价群体,找出群体最 通过仿真,笔者发现基本蝙蝠算法存在易被局部极 优位置:然后,分别按式(1)和(2)更新个体的飞行 值吸引、发生过早收敛、后期收敛速度慢等问题 速度和位置: 本文基于蝙蝠觅食的特点,在分析原有算法优 =1+(x-x)·f, (1) 化机理和局限性的基础上,提出了一种蝙蝠优化算 x=x1+ (2) 法,在优化过程中采用Levy flight策略来模拟蝙蝠的搜 式中:分别表示蝙蝠i在t-1和t时刻的飞行 索捕食行为,更加贴近蝙蝠真实捕食过程,从本质上提 速度:x表示蝙蝠i在t时刻的空间位置,x·表示在 升了算法的优化性能采用基准测试函数对所提算法进 当前群体中最佳蝙蝠所处位置:为蝙蝠i搜寻猎 行仿真测试,并与基本蝙蝠算法、PS0算法进行对比, 物时使用的脉冲频率,f∈[f。∫]为搜索脉冲频 测试结果验证了所提算法的可行性和优越性, 率范围 1基本蝙蝠算法优化机理和局限 根据生物学机理可知,在搜寻猎物过程中,蝙蝠 初始阶段发出的超声波脉冲音强大而频度低,有助于 1.1算法仿生原理及数学模型 在更广泛的空间搜索,发现猎物后,就逐渐减小脉冲音 蝙蝠在搜寻猎物时,每秒发出大约10~20个、 强同时增加脉冲发射次数,以利于精确掌握猎物的空 音强达110dB的超声波脉冲,脉冲音强在搜寻猎物 间位置,故用式(3)和(4)来模拟这种搜索特点, 时最大,在飞向猎物时逐渐减小,同时脉冲频度逐渐 rt'=[1-exp(-y×t)], (3) 增加,达到每秒发射约200个脉冲.脉冲音强大有助 A+1=a×A (4) 于蝙蝠探测更远的距离,脉冲频度高有助于精确掌 式中:表示蝙蝠i的最大脉冲频度;表示在t+1 握猎物不断变化的空间位置.通过这套精巧的“声呐 时刻蝙蝠i的脉冲频度:y是脉冲频度增加系数,为 系统”,蝙蝠能够在黑暗的环境中躲避如发丝粗细 大于零的常数;4:表示t时刻蝙蝠i发射脉冲的音强:α 的障碍物且能捕食猎物. 是脉冲音强衰减系数,通常取[0,1]上的常数 蝙蝠在复杂环境中精确定位、捕食的情形为模 基本蝙蝠算法流程图如图1所示,其中R,、R, 拟其生物学机理进行优化带来了启发,蝙蝠算法是 是随机生成数 初始化种群,找出最住蝙蝠个体 用新位置替换先前位置 更新速度和位置 新位置优于当 R<r N 新位置由当 前最佳位置 前最佳位置 扰动产生 Y 接受更新后位置 当前最佳 替换当前最佳位置,调器 位置不变 脉冲频度r和脉冲音强A 评估新位置 满足要求 N 新位置优于先前位 Y 置并且R<A, 输出结果 IN 原位置不变 图1基本蝙蝠算法流程 Fig.1 Procedure of original bat algorithm 1.2基本蝙蝠算法的局限性 1)算法缺乏变异机制,种群不易保持多样性.群 根据基本蝙蝠算法的优化机理,发现算法在两 智能算法是否高效,重要一点就是要具备优良的变 方面存在固有不足: 异机制,维持种群多样性,从而保持持续进化能力
的生物学特性,Yang 曾提出一种基于随机优化的蝙 蝠算法[5] ,该算法具有模型简单、收敛速度快、可并 行处理等特点,在工程设计中得到了初步应用[6⁃7] . 通过仿真,笔者发现基本蝙蝠算法存在易被局部极 值吸引、发生过早收敛、后期收敛速度慢等问题. 本文基于蝙蝠觅食的特点,在分析原有算法优 化机理和局限性的基础上,提出了一种蝙蝠优化算 法,在优化过程中采用 Lévy flight 策略来模拟蝙蝠的搜 索捕食行为,更加贴近蝙蝠真实捕食过程,从本质上提 升了算法的优化性能.采用基准测试函数对所提算法进 行仿真测试,并与基本蝙蝠算法、PSO 算法进行对比, 测试结果验证了所提算法的可行性和优越性. 1 基本蝙蝠算法优化机理和局限 1.1 算法仿生原理及数学模型 蝙蝠在搜寻猎物时,每秒发出大约 10 ~ 20 个、 音强达 110 dB 的超声波脉冲,脉冲音强在搜寻猎物 时最大,在飞向猎物时逐渐减小,同时脉冲频度逐渐 增加,达到每秒发射约 200 个脉冲.脉冲音强大有助 于蝙蝠探测更远的距离,脉冲频度高有助于精确掌 握猎物不断变化的空间位置.通过这套精巧的“声呐 系统”,蝙蝠能够在黑暗的环境中躲避如发丝粗细 的障碍物且能捕食猎物. 蝙蝠在复杂环境中精确定位、捕食的情形为模 拟其生物学机理进行优化带来了启发,蝙蝠算法是 基于群体进化的算法,首先在可行解空间随机初始 化种群,即确定个体的初始位置和初始速度,其中位 置用于表征问题解;进而通过评价群体,找出群体最 优位置;然后,分别按式(1)和(2)更新个体的飞行 速度和位置: v t i = v t-1 i + (x t i - x ∗ )·f i, (1) x t i = x t-1 i + v t i . (2) 式中:v t-1 i 、v t i 分别表示蝙蝠 i 在 t-1 和 t 时刻的飞行 速度;x t i 表示蝙蝠 i 在 t 时刻的空间位置,x ∗ 表示在 当前群体中最佳蝙蝠所处位置;f i 为蝙蝠 i 搜寻猎 物时使用的脉冲频率,f i∈[ fmin ,fmax ]为搜索脉冲频 率范围. 根据生物学机理可知,在搜寻猎物过程中,蝙蝠 初始阶段发出的超声波脉冲音强大而频度低,有助于 在更广泛的空间搜索,发现猎物后,就逐渐减小脉冲音 强同时增加脉冲发射次数,以利于精确掌握猎物的空 间位置,故用式(3)和(4) [5]来模拟这种搜索特点. r t+1 i = r 0 i [1 - exp( - γ × t)], (3) A t+1 i = α × A t i . (4) 式中:r 0 i 表示蝙蝠 i 的最大脉冲频度;r t+1 i 表示在 t+1 时刻蝙蝠 i 的脉冲频度;γ 是脉冲频度增加系数,为 大于零的常数;A t i 表示 t 时刻蝙蝠 i 发射脉冲的音强;α 是脉冲音强衰减系数,通常取[0,1]上的常数. 基本蝙蝠算法流程图如图 1 所示,其中 R1 、R2 是随机生成数. 图 1 基本蝙蝠算法流程 Fig.1 Procedure of original bat algorithm 1.2 基本蝙蝠算法的局限性 根据基本蝙蝠算法的优化机理,发现算法在两 方面存在固有不足: 1)算法缺乏变异机制,种群不易保持多样性.群 智能算法是否高效,重要一点就是要具备优良的变 异机制,维持种群多样性,从而保持持续进化能力. 第 3 期 刘长平,等:具有 Lévy 飞行特征的蝙蝠算法 ·241·

·242· 智能系统学报 第8卷 从基本蝙蝠算法的优化过程来看,算法缺乏有效的 分布的概率密度函数服从高斯分布;当α=1,B=0 变异机制,个体容易被局部极值吸引而导致早熟收 时,服从柯西分布:a=0.5,B=1时,服从Ley分布.由 敛基本算法采用了向当前最优个体学习进行速度 于0<Q<2时,Lévy分布的方差发散且以指数形式增长, 更新,从而实现位置更新,若当前最优个体一旦被局 因此在Léy飞行过程中会发生大的跳跃且方向多变, 部极值吸引,并没有有效机制来摆脱束缚,群体迅速 其典型轨迹表现为由较小跳跃组成的聚集被较大的跳 丧失多样性进而失去进化能力,特别在高维复杂形 跃分隔开的现象,图2为Lévy飞行的轨迹模拟图(图 态表现尤为明显.脉冲频度τ和脉冲音强A只决定 中“*”表示起始点,“7”表示终点) 算法以一定概率接受更新后的位置,但对克服局部 吸引子的吸引效果并不佳 2)算法仿生过程与真实情况有较大差异.原算 法将蝙蝠搜寻猎物的行为抽象为概率选择加简单随 机搜索过程,这样处理虽然简化了算法模型,但失真 较大,不能有效模拟蝙蝠真实捕食行为,没有体现出 算法的生物智能, 图2Lévy飞行轨迹模拟 2具有Léy飞行特征的蝙蝠算法 Fig.2 Simulation tracks of Levy flights 受此启发,本文采用Lévy飞行模式来模拟蝙蝠 2.1自然界中的Léy飞行行为 的飞行搜索行为,充分利用Léy飞行随机游走的特 研究发现,觅食者在一个食物来源不集中、不可 性,在搜索过程中借助Lévy飞行会产生较大跳跃且 预测的环境中找到食物的理想方式,应采取一种 方向多次急剧改变,来有效避免蝙蝠个体被局部吸 “Lévy飞行”搜索策略,在这种形式的搜索中,短距 引子束缚,同时拓展了搜索空间,能够有效提高蝙蝠 离的探索性蹦蹦跳跳与偶尔较长距离的行走相间 算法在高维复杂空间的优化效果,再结合蝙蝠的回 如Viswanathan等[s]利用GPS对信天翁觅食行为 声定位特征,有助于从本质上提升蝙蝠算法的性能. 进行研究,发现飞行路线具有类似Lé四飞行特征: 改进算法中用式(6)来替代原算法中的速度和位置 Reynolds等[oi对蜜蜂以及果蝇觅食轨迹进行观 更新操作(即式(1)、(2). 察,发现其飞行轨迹中也呈现出Lévy飞行特征;此 x*'=x+L(A)☒(x-x). (6) 外,在针对驯鹿[2)、蜘蛛猴)、灰海豹、狒狒 式中:x表示蝙蝠i在第t次搜寻中的空间位置,x 以及其他14种海洋捕食物种等生物[16]的研究中都 表示在当前群体中最佳蝙蝠所处位置:L(入)表示 发现了Levy飞行或者近似Levy飞行行为,甚至在 跳跃步长服从Lévy分布的随机搜索向量,入(1< 人的行为中也有形似Léy飞行行为的存在1.一系 入≤3)为尺度参数:⑧代表矢量运算 列重要研究证明),当目标位置随机且稀疏分布 2.3算法步骤 时,对于N个相互独立的探索者来说,Lévy飞行行 综上所述,具有Léy飞行特征的蝙蝠算法步骤 为是最理想的搜索策略 如下: 2.2改进蝙蝠算法及数学模型 1)初始化算法基本参数:设置蝙蝠数目m、个 从数学角度看,Lévy飞行行为体现出的是一类 体i最大脉冲频度°和最大脉冲音强A,、频度增加 非高斯随机过程,其平稳增量服从Léy稳定分布. 系数y、音强衰减系数a、Lévy飞行尺度参数入、最大 Léy稳定分布的概率密度函数没有统一的形式,可 迭代次数N或搜索精度ε; 以用其特征函数的连续傅里叶变换来定义,如式 2)随机初始化蝙蝠位置x(i=1,2,…,m),找出 (5)所示: 群体中处于最佳位置x·的个体; P.(k)-( 3)生成随机数R1,如R,<T:,按照式(6)更新蝙 蝠当前位置:否则对蝙蝠当前位置进行随机扰动,用 5 扰动后的位置代替当前位置: 式中:a∈(0,1)U(1,2]为特征指数:B∈[-1,1]表 4)生成随机数R2,如R,<A:并且蝙蝠当前位置 示偏度参数,当B分别为正、零、负时,分布分别右 得到改善,则飞至更新后位置; 偏、对称、左偏:是位移,描述均值;σ为尺度,描述 5)若更新位置后蝙蝠i优于群体中最佳蝙蝠, 随机变量发散的程度.特别地,当α=2时,Léy稳定 则替换最佳蝙蝠个体,并根据式(3)、(4)调整脉冲
从基本蝙蝠算法的优化过程来看,算法缺乏有效的 变异机制,个体容易被局部极值吸引而导致早熟收 敛.基本算法采用了向当前最优个体学习进行速度 更新,从而实现位置更新,若当前最优个体一旦被局 部极值吸引,并没有有效机制来摆脱束缚,群体迅速 丧失多样性进而失去进化能力,特别在高维复杂形 态表现尤为明显.脉冲频度 r 和脉冲音强 A 只决定 算法以一定概率接受更新后的位置,但对克服局部 吸引子的吸引效果并不佳. 2)算法仿生过程与真实情况有较大差异.原算 法将蝙蝠搜寻猎物的行为抽象为概率选择加简单随 机搜索过程,这样处理虽然简化了算法模型,但失真 较大,不能有效模拟蝙蝠真实捕食行为,没有体现出 算法的生物智能. 2 具有 Lévy 飞行特征的蝙蝠算法 2.1 自然界中的 Lévy 飞行行为 研究发现,觅食者在一个食物来源不集中、不可 预测的环境中找到食物的理想方式,应采取一种 “Lévy 飞行”搜索策略,在这种形式的搜索中,短距 离的探索性蹦蹦跳跳与偶尔较长距离的行走相间. 如 Viswanathan 等[8⁃9] 利用 GPS 对信天翁觅食行为 进行研究,发现飞行路线具有类似 Lévy 飞行特征; Reynolds 等[10⁃11]对蜜蜂以及果蝇觅食轨迹进行观 察,发现其飞行轨迹中也呈现出 Lévy 飞行特征;此 外,在针对驯鹿[12] 、蜘蛛猴[13] 、灰海豹[14] 、狒狒[15] 以及其他 14 种海洋捕食物种等生物[16] 的研究中都 发现了 Lévy 飞行或者近似 Lévy 飞行行为,甚至在 人的行为中也有形似 Lévy 飞行行为的存在[17] .一系 列重要研究证明[18] ,当目标位置随机且稀疏分布 时,对于 N 个相互独立的探索者来说,Lévy 飞行行 为是最理想的搜索策略. 2.2 改进蝙蝠算法及数学模型 从数学角度看,Lévy 飞行行为体现出的是一类 非高斯随机过程,其平稳增量服从 Lévy 稳定分布. Lévy 稳定分布的概率密度函数没有统一的形式,可 以用其特征函数的连续傅里叶变换来定义,如式 (5)所示: pα,β(k) = exp iμk - σ α | k | α 1 - iβ k | k | tan( π 2 α) æ è ç ö ø ÷ é ë ê ê ù û ú ú . (5) 式中:α∈(0,1)∪(1,2]为特征指数;β∈[ -1,1]表 示偏度参数,当 β 分别为正、零、负时,分布分别右 偏、对称、左偏;μ 是位移,描述均值;σ 为尺度,描述 随机变量发散的程度.特别地,当 α = 2 时,Lévy 稳定 分布的概率密度函数服从高斯分布;当 α = 1,β = 0 时,服从柯西分布;α = 0.5,β = 1 时,服从 Lévy 分布.由 于0<α<2 时,Lévy 分布的方差发散且以指数形式增长, 因此在 Lévy 飞行过程中会发生大的跳跃且方向多变, 其典型轨迹表现为由较小跳跃组成的聚集被较大的跳 跃分隔开的现象,图 2 为 Lévy 飞行的轨迹模拟图(图 中“∗”表示起始点,“▽”表示终点). 图 2 Lévy 飞行轨迹模拟 Fig.2 Simulation tracks of Lévy flights 受此启发,本文采用 Lévy 飞行模式来模拟蝙蝠 的飞行搜索行为,充分利用 Lévy 飞行随机游走的特 性,在搜索过程中借助 Lévy 飞行会产生较大跳跃且 方向多次急剧改变,来有效避免蝙蝠个体被局部吸 引子束缚,同时拓展了搜索空间,能够有效提高蝙蝠 算法在高维复杂空间的优化效果,再结合蝙蝠的回 声定位特征,有助于从本质上提升蝙蝠算法的性能. 改进算法中用式(6)来替代原算法中的速度和位置 更新操作(即式(1)、(2)). x t+1 i = x t i + Lévy(λ) (x t i - x ∗ ). (6) 式中:x t i 表示蝙蝠 i 在第 t 次搜寻中的空间位置,x ∗ 表示在当前群体中最佳蝙蝠所处位置;Lévy(λ)表示 跳跃步长服从 Lévy 分布的随机搜索向量, λ( 1 < λ≤3)为尺度参数;代表矢量运算. 2.3 算法步骤 综上所述,具有 Lévy 飞行特征的蝙蝠算法步骤 如下: 1)初始化算法基本参数:设置蝙蝠数目 m、个 体 i 最大脉冲频度 r 0 i 和最大脉冲音强 Ai、频度增加 系数 γ、音强衰减系数 α、Lévy 飞行尺度参数 λ、最大 迭代次数 Nmax或搜索精度 ε; 2)随机初始化蝙蝠位置 x(i = 1,2,…,m),找出 群体中处于最佳位置 x ∗的个体; 3)生成随机数 R1 ,如 R1 <ri,按照式(6)更新蝙 蝠当前位置;否则对蝙蝠当前位置进行随机扰动,用 扰动后的位置代替当前位置; 4)生成随机数 R2 ,如 R2<Ai 并且蝙蝠当前位置 得到改善,则飞至更新后位置; 5)若更新位置后蝙蝠 i 优于群体中最佳蝙蝠, 则替换最佳蝙蝠个体,并根据式(3)、(4)调整脉冲 ·242· 智 能 系 统 学 报 第 8 卷

第3期 刘长平,等:具有Ly飞行特征的蝙蝠算法 ·243· 频度r:和脉冲音强A: 入8),否则转3),进行下一次搜索: 6)对蝙蝠群体进行评估,找出当前最佳蝙蝠及 8)输出全局极值点和最优个体值. 所处空间位置: 改进蝙蝠算法流程如图3所示。 7)当满足搜索精度或达到最大搜索次数则转 初始化种群,找出最住蝙蝠个体 用新位置替换先前位置 N 新位置由当 R<r 前个体位置 新位置优于当 扰动产生 前最佳位置 Y 采用Levy Flight Y 模式更新位置 当前最佳 替换当前最佳位置调整 位置不变 脉冲频度和脉冲音强A 评估新位置 满足要求 N 新位置优于先前位 Y 置并且R<A, 输出结果 TN 原位置不变 图3改进蝙蝠算法流程 Fig.3 Procedure of improved bat algorithm 3仿真实验 法中:个体i最大脉冲频度=0.75,最大脉冲音强 A,=0.75,脉冲音强衰减系数α=0.99,脉冲频度增加系 为验证本文提出的具有Lévy飞行特征的蝙蝠 数y=0.04,Ley飞行尺度参数A=1.5.基本蝙蝠算法 算法性能,选取了7个标准测试函数进行仿真测试, 中:搜索脉冲频率范围为[-1,1],其余参数同上粒子 并与基本蝙蝠算法和粒子群算法[19进行对比。 群算法中:采用线性递减的惯性权重W=0.9,Wm= 3.1参数设置 0.4:学习因子C,=C2=1.4962.以上3种算法最大搜索 蝙蝠算法中涉及的各种参数取值目前尚无确切 次数均为Nm=3000,群体数m=40. 的理论依据,本文所设置的参数值是根据反复实验 3.2测试函数 获得的经验值来确定.具有Léy飞行特征的蝙蝠算 测试函数如表1所示 表1标准测试函数 Table 1 Standard test functions 函数名 函数表达式 搜索空间 理论最优解 Schaffer F6 sin2√x+-0.5 f(x)= 1+0.01(+5-0.5 [-100,100] f(0,0)=-1 Shubert )-2is(+1)x,上[01k,切 [-10,10] f2(x)=-186.7309 Michalewicz 6()-克[sm(/m]产,m=10 D=5f5(x*)=-4.6877 [0,r] D=10f5(x)=-9.6602 Rastrigin (x)=2[-10es(2ms,)+10] [-5.12,5.12] f(0,…,0)=0 Schwefel 6=41&g29xD-足m(/) [-500,500] f5(420.96,…,420.96)=0 Griewank 6()1 [-600.600] 4000台 f(0,…,0)=0 Rosenbrock f(x)= 三【-1)+10(2] [-2.048,2.048] f(1,…,1)=0 注:x·表示在搜索区域内最优位置不惟一
频度 ri 和脉冲音强 Ai; 6)对蝙蝠群体进行评估,找出当前最佳蝙蝠及 所处空间位置; 7)当满足搜索精度或达到最大搜索次数则转 入 8),否则转 3),进行下一次搜索; 8)输出全局极值点和最优个体值. 改进蝙蝠算法流程如图 3 所示. 图 3 改进蝙蝠算法流程 Fig.3 Procedure of improved bat algorithm 3 仿真实验 为验证本文提出的具有 Lévy 飞行特征的蝙蝠 算法性能,选取了 7 个标准测试函数进行仿真测试, 并与基本蝙蝠算法和粒子群算法[19]进行对比. 3.1 参数设置 蝙蝠算法中涉及的各种参数取值目前尚无确切 的理论依据,本文所设置的参数值是根据反复实验 获得的经验值来确定.具有 Lévy 飞行特征的蝙蝠算 法中:个体 i 最大脉冲频度 r 0 i = 0.75,最大脉冲音强 Ai =0.75,脉冲音强衰减系数 α = 0.99,脉冲频度增加系 数 γ=0.04,Lévy 飞行尺度参数 λ = 1.5.基本蝙蝠算法 中:搜索脉冲频率范围为[-1,1],其余参数同上.粒子 群算法中:采用线性递减的惯性权重 Wmax =0.9,Wmin = 0.4;学习因子 C1 =C2 = 1.496 2.以上 3 种算法最大搜索 次数均为 Nmax =300 0,群体数 m=40. 3.2 测试函数 测试函数如表 1 所示. 表 1 标准测试函数 Table 1 Standard test functions 函数名 函数表达式 搜索空间 理论最优解 Schaffer F6 f 1(x)= sin 2 x 2 1 +x 2 2 -0.5 [1+0.001(x 2 1 +x 2 2 )] 2 -0.5 [-100,100] f 1(0,0)= -1 Shubert f 2(x)= 5 i= 1 icos[(i+1)x1 +i] 5 i= 1 jcos[(j+1)x2 +j] [-10,10] f 2(x ∗ )= -186.730 9 Michalewicz f 3(x)= - D i= 1 sin(xi)[sin(ix 2 i / π] 2m ,m= 10 [0,π] D= 5,f 3(x ∗ )= -4.687 7 D= 10,f 3(x ∗ )= -9.660 2 Rastrigin f 4(x)= D i= 1 [x 2 i -10cos(2πxi)+10] [-5.12,5.12] f 4(0,…,0)= 0 Schwefel f 5(x)= 418.982 9×D- D i= 1 xi sin( | xi | ) [-500,500] f 5(420.96,…,420.96)= 0 Griewank f 6(x)= 1 400 0 D i= 1 (x 2 i )- D i= 1 cos( xi i )+1 [-600,600] f 6(0,…,0)= 0 Rosenbrock f 7(x)= D-1 i= 1 [(xi -1) 2+100(x 2 i -xi+1 ) 2 ] [-2.048,2.048] f 7(1,…,1)= 0 注:x ∗ 表示在搜索区域内最优位置不惟一 第 3 期 刘长平,等:具有 Lévy 飞行特征的蝙蝠算法 ·243·
·244- 智能系统学报 第8卷 函数∫~f。均是非线性多峰多极值函数,可以 多个极小值呈规律性分布:Rosenbrock函数是单峰 有效检验算法的全局搜索性能、保持群体多样性和 连续函数,在局部最优和全局最小之间有一个非常 避免早熟的收敛能力.Schaffer F6函数在搜索空间 狭窄的波谷,极小点所在的山谷易于找到,但极难收 内具有强烈振荡的特点:Shubert函数在搜索区域内 敛到全局最优点,是测试算法探索、开发能力的经典 约有760个局部极值和18个全局最优点: 函数. Michalewicz函数有n!个局部最小值,参数m定义 3.3测试结果及分析 了峰谷和边缘的“陡峭度”,m较大时,搜索会变得 实验规定当实际寻优值与理论最优值的相对误 很困难:Rastrigrin函数在解空间内存在大约l0n(n 差小于1%时,算作找到最优解,每种算法独立运行 为解空间维数)个局部极小点;Schwefel函数有一个 10次,测试结果如表2所示.表中LBA代表具有 非常“粗糙”的适应度表面,全局最优具有很大欺骗 Ley飞行特征的蝙蝠算法,BA代表基本蝙蝠算法, 性,种群极易陷入局部极值中,是测试算法全局收敛 PS0代表粒子群算法.限于篇幅,文中仅列出了部分 性能的极佳函数:Griewank函数有众多局部极值且 寻优效果图,分别如图4(a)~(f)所示 表2LBA、BA、PSO3种算法测试结果对比 Table 2 Experimental results comparison of LBA,BA,and PSO algorithm 实际找到最优值 平均寻优值 寻优成功率/% 函数 维数 LBA BA PSO LBA BA PSO LBA BA PSO f(x) 2 -1 -1 -1 -0.9968 -0.9884 -0.9977 86.9 14.7 81.7 (x) -186.7309-186.7309 -186.7309-186.6082-182.6566-185.4550 94.092.681.5 5 -4.6877 -4.3749 -4.6877 -4.6536 -4.1315 -4.5209 93.4 0.0 78.9 f3(x) 10 -9.6600 -6.3864 -7.7188 -9.2608 -6.2895 -7.2244 1.6 0.0 0.0 5 1.4566×103 2.9849 0.9949 0.6601 8.5559 1.8702 79.7 0.0 0.0 f(x) 10 2.6196×10 20.1046 6.9649 5.3026 20.9506 12.1834 20.1 0.0 0.0 5 6.3638×105 236.8767 118.4383 22.5173 382.2819 127.1291 72.6 0.0 0.0 (x) 10 0.0053 870.0786 238.3939 202.1774 1123.6937 296.2766 11.9 0.0 0.0 10 7.4889×104 1.5149 0.2024 1.0879 3.0541 0.9689 31.3 0.0 0.0 fo(x) 20 6.6457×105 0.0236 0.4951 5.8559 4.2766 2.5342 40.60.0 0.0 10 0.0026 0.4699 3.9141 5.4967 2.7931 10.0863 55.60.0 0.0 (x) 20 0.0058 14.4088 19.1400 25.3166 24.0294 39.5790 12.4 0.0 0.0 对于函数f,3种算法均收敛到了最优解,反映 度、寻优率和收敛速度方面均优于BA、PSO,表现出良 出3种算法在低维复杂环境下具有良好的进化机制和 好的全局寻优能力和较高的搜索精度,说明采用Léy 搜索能力.函数~。均是高维、多峰、含有大量局部极 飞行策略来模拟蝙蝠的捕食过程更为真实有效,验证 值的多模态函数,PS0仅在f(D=5)情况下找到了最 了所提算法的可行性和有效性 优解,其余状态下BA、PSO均未搜索到最优解对于上 -6.0m 述函数,LBA在不同维度的搜索空间均收敛到了最优 -6.5 解,而且寻优精度和收敛速度也远高于其他2种算法, -7.0 寻优性能如图4(a)~(d)所示.函数f)虽是单峰连续函 -7.5 数,但取值区间走势平坦只为算法提供少量信息,极难 9-8.0 收敛到全局最优点测试中LBA在f,(D=10)情况下仍 -8.5h …BA ---PS0 能以较高精度找到最优解,而BA、PSO则早熟收敛到 -9.0 LBA 局部极值,如图4(e)所示.在f,(D=20)情况下,LBA仍 -9.5 10 0 0.51.0 然可以以较高精度收敛到最优解,且精度远高于对比 1.52.02.5 30 迭代次数 算法,显示出改进算法具有良好的探索、开发能力,如 (a)Michalewicz函数(D=l0) 图4()所示.综合来看,在同等条件下,LBA在寻优精
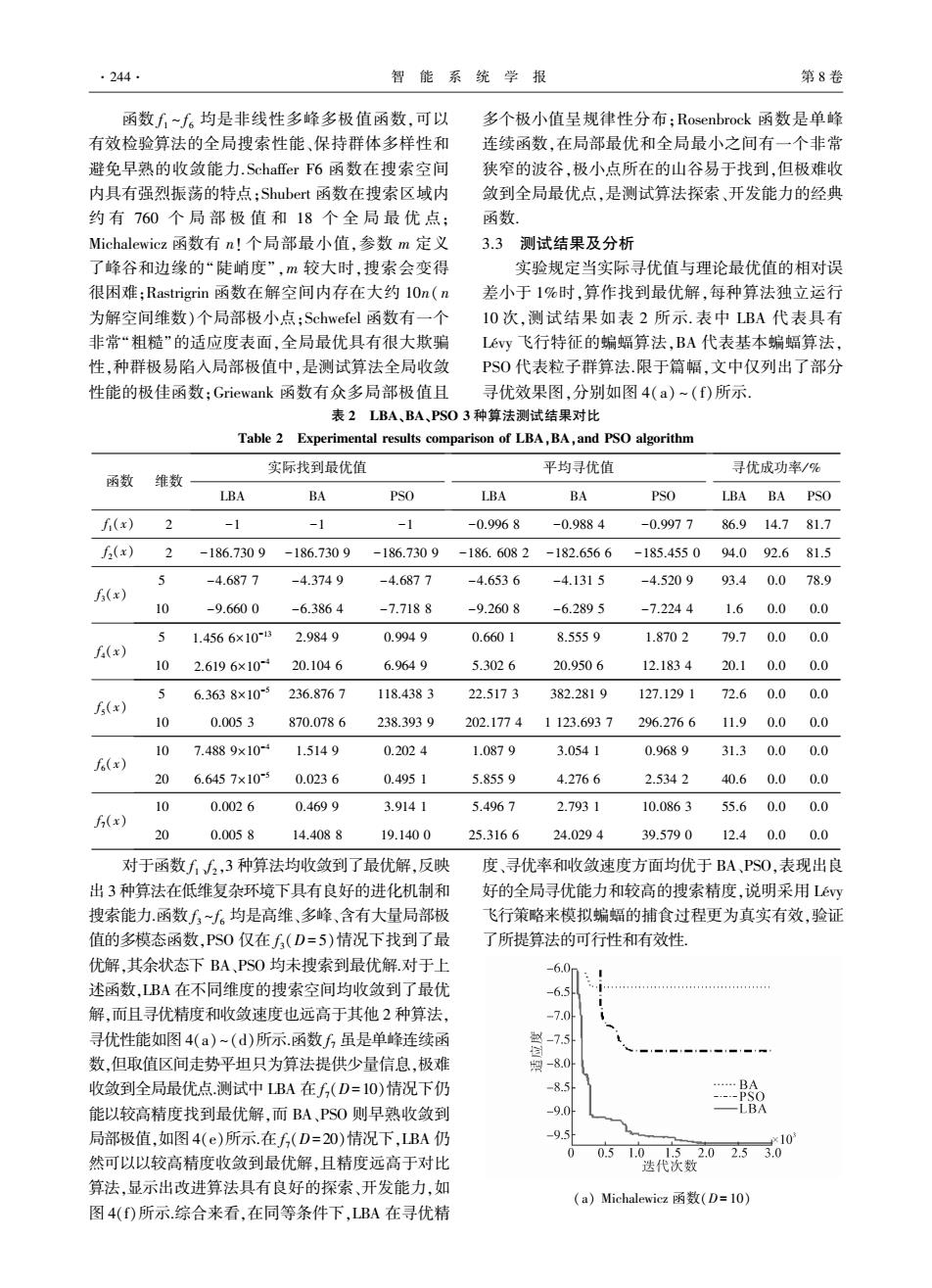
函数 f 1 ~ f 6 均是非线性多峰多极值函数,可以 有效检验算法的全局搜索性能、保持群体多样性和 避免早熟的收敛能力. Schaffer F6 函数在搜索空间 内具有强烈振荡的特点;Shubert 函数在搜索区域内 约 有 760 个 局 部 极 值 和 18 个 全 局 最 优 点; Michalewicz 函数有 n! 个局部最小值,参数 m 定义 了峰谷和边缘的“陡峭度”,m 较大时,搜索会变得 很困难;Rastrigrin 函数在解空间内存在大约 10n( n 为解空间维数)个局部极小点;Schwefel 函数有一个 非常“粗糙”的适应度表面,全局最优具有很大欺骗 性,种群极易陷入局部极值中,是测试算法全局收敛 性能的极佳函数;Griewank 函数有众多局部极值且 多个极小值呈规律性分布;Rosenbrock 函数是单峰 连续函数,在局部最优和全局最小之间有一个非常 狭窄的波谷,极小点所在的山谷易于找到,但极难收 敛到全局最优点,是测试算法探索、开发能力的经典 函数. 3.3 测试结果及分析 实验规定当实际寻优值与理论最优值的相对误 差小于 1%时,算作找到最优解,每种算法独立运行 10 次,测试结果如表 2 所示. 表中 LBA 代表具有 Lévy 飞行特征的蝙蝠算法,BA 代表基本蝙蝠算法, PSO 代表粒子群算法.限于篇幅,文中仅列出了部分 寻优效果图,分别如图 4(a) ~ (f)所示. 表 2 LBA、BA、PSO 3 种算法测试结果对比 Table 2 Experimental results comparison of LBA,BA,and PSO algorithm 函数 维数 实际找到最优值 LBA BA PSO 平均寻优值 LBA BA PSO 寻优成功率/ % LBA BA PSO f 1(x) 2 -1 -1 -1 -0.996 8 -0.988 4 -0.997 7 86.9 14.7 81.7 f 2(x) 2 -186.730 9 -186.730 9 -186.730 9 -186. 608 2 -182.656 6 -185.455 0 94.0 92.6 81.5 f 3(x) 5 -4.687 7 -4.374 9 -4.687 7 -4.653 6 -4.131 5 -4.520 9 93.4 0.0 78.9 10 -9.660 0 -6.386 4 -7.718 8 -9.260 8 -6.289 5 -7.224 4 1.6 0.0 0.0 f 4(x) 5 1.456 6×10 -13 2.984 9 0.994 9 0.660 1 8.555 9 1.870 2 79.7 0.0 0.0 10 2.619 6×10 -4 20.104 6 6.964 9 5.302 6 20.950 6 12.183 4 20.1 0.0 0.0 f 5(x) 5 6.363 8×10 -5 236.876 7 118.438 3 22.517 3 382.281 9 127.129 1 72.6 0.0 0.0 10 0.005 3 870.078 6 238.393 9 202.177 4 1 123.693 7 296.276 6 11.9 0.0 0.0 f 6(x) 10 7.488 9×10 -4 1.514 9 0.202 4 1.087 9 3.054 1 0.968 9 31.3 0.0 0.0 20 6.645 7×10 -5 0.023 6 0.495 1 5.855 9 4.276 6 2.534 2 40.6 0.0 0.0 f 7(x) 10 0.002 6 0.469 9 3.914 1 5.496 7 2.793 1 10.086 3 55.6 0.0 0.0 20 0.005 8 14.408 8 19.140 0 25.316 6 24.029 4 39.579 0 12.4 0.0 0.0 对于函数 f 1、f 2,3 种算法均收敛到了最优解,反映 出 3 种算法在低维复杂环境下具有良好的进化机制和 搜索能力.函数 f 3 ~f 6 均是高维、多峰、含有大量局部极 值的多模态函数,PSO 仅在 f 3(D= 5)情况下找到了最 优解,其余状态下 BA、PSO 均未搜索到最优解.对于上 述函数,LBA 在不同维度的搜索空间均收敛到了最优 解,而且寻优精度和收敛速度也远高于其他 2 种算法, 寻优性能如图 4(a) ~(d)所示.函数 f 7 虽是单峰连续函 数,但取值区间走势平坦只为算法提供少量信息,极难 收敛到全局最优点.测试中 LBA 在 f 7(D=10)情况下仍 能以较高精度找到最优解,而 BA、PSO 则早熟收敛到 局部极值,如图 4(e)所示.在 f 7(D=20)情况下,LBA 仍 然可以以较高精度收敛到最优解,且精度远高于对比 算法,显示出改进算法具有良好的探索、开发能力,如 图 4(f)所示.综合来看,在同等条件下,LBA 在寻优精 度、寻优率和收敛速度方面均优于 BA、PSO,表现出良 好的全局寻优能力和较高的搜索精度,说明采用 Lévy 飞行策略来模拟蝙蝠的捕食过程更为真实有效,验证 了所提算法的可行性和有效性. (a) Michalewicz 函数(D= 10) ·244· 智 能 系 统 学 报 第 8 卷
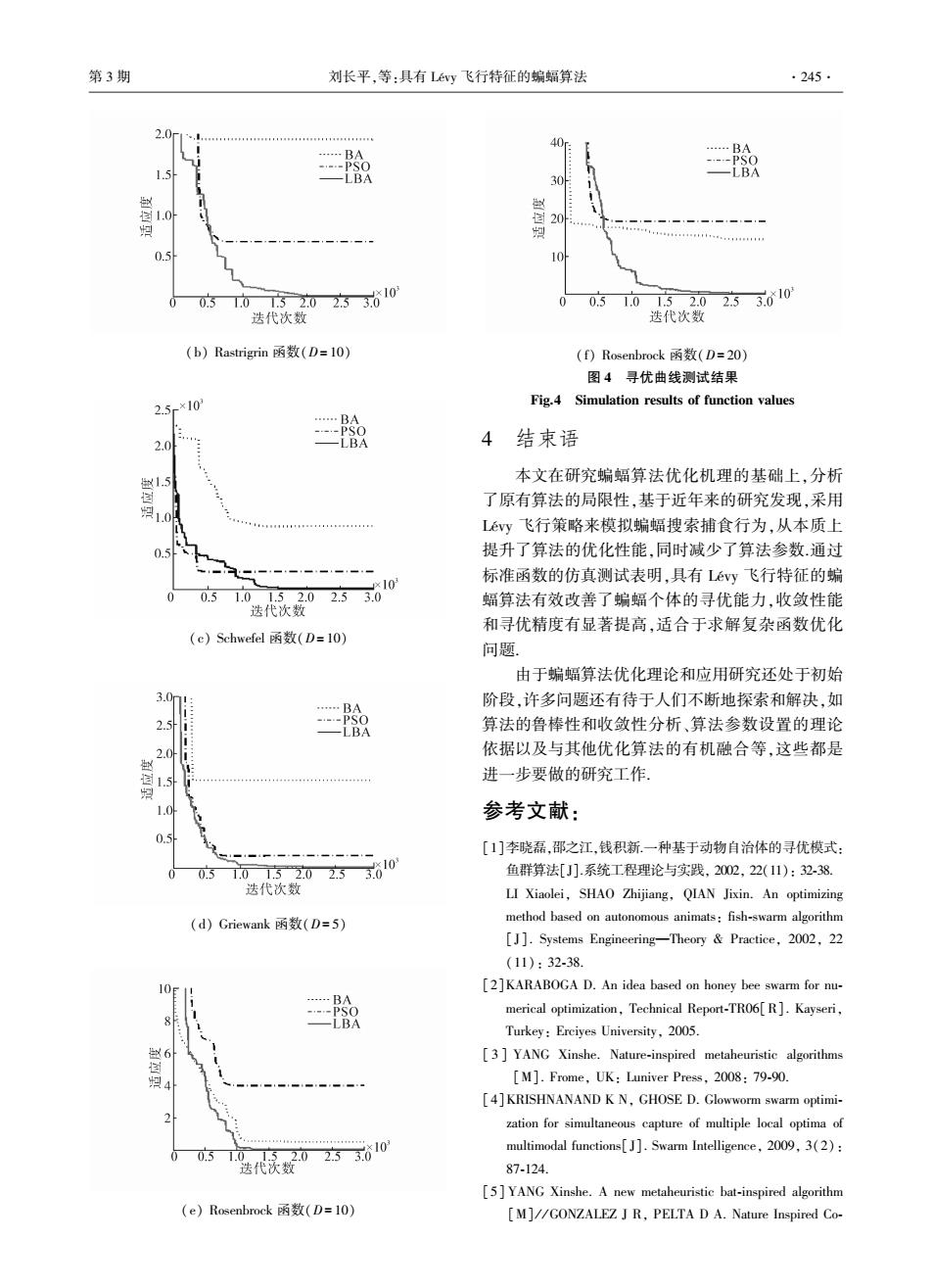
第3期 刘长平,等:具有Ly飞行特征的蝙蝠算法 ·245· 2.0l 40 …BA 1.5 --PS0 LBA 30 自1.0h 国 20 0.5 10 0.3 0202方610 00.31052.0253.ǒ10 迭代次数 迭代次数 (b)Rastrigrin函数(D=10) (f)Rosenbrock函数(D=20) 图4寻优曲线测试结果 2.5r×10 Fig.4 Simulation results of function values ......BA ---pS0 2.0 LBA 4结束语 1.5 本文在研究蝙蝠算法优化机理的基础上,分析 了原有算法的局限性,基于近年来的研究发现,采用 10 1t非0891目11非5ag444104g44111 Levy飞行策略来模拟蝙蝠搜索捕食行为,从本质上 0.5 提升了算法的优化性能,同时减少了算法参数通过 10 标准函数的仿真测试表明,具有Lévy飞行特征的蝙 00.51.01.52.02.53.0 蝠算法有效改善了蝙蝠个体的寻优能力,收敛性能 迭代次数 和寻优精度有显著提高,适合于求解复杂函数优化 (c)Schwefel函数(D=l0) 问题 由于蝙蝠算法优化理论和应用研究还处于初始 5. …BA 阶段,许多问题还有待于人们不断地探索和解决,如 2.5 ---PSO —LBA 算法的鲁棒性和收敛性分析、算法参数设置的理论 2.0h 依据以及与其他优化算法的有机融合等,这些都是 1.5 进一步要做的研究工作, 1.0 参考文献: 0.5 [1]李晓磊,邵之江,钱积新.一种基于动物自治体的寻优模式: 0.5 02023ǒ10 鱼群算法[J】.系统工程理论与实践,2002,22(11):32-38. 迭代次数 LI Xiaolei,SHAO Zhijiang,QIAN Jixin.An optimizing (d)Griewank函数(D=5) method based on autonomous animats:fish-swarm algorithm [J].Systems Engineering-Theory Practice,2002,22 (11):32-38. [2]KARABOGA D.An idea based on honey bee swarm for nu- PSO merical optimization,Technical Report-TR06[R].Kayseri, LBA Turkey:Erciyes University,2005. 6 [3]YANG Xinshe.Nature-inspired metaheuristic algorithms [M].Frome,UK:Luniver Press,2008:79-90. [4]KRISHNANAND K N,GHOSE D.Glowworm swarm optimi- zation for simultaneous capture of multiple local optima of multimodal functions[J].Swarm Intelligence,2009,3(2): 0.51.0 .0 代次数 87-124. [5]YANG Xinshe.A new metaheuristic bat-inspired algorithm (e)Rosenbrock函数(D=10) [M]//GONZALEZ J R,PELTA D A.Nature Inspired Co-
(b) Rastrigrin 函数(D= 10) (c) Schwefel 函数(D= 10) (d) Griewank 函数(D= 5) (e) Rosenbrock 函数(D= 10) (f) Rosenbrock 函数(D= 20) 图 4 寻优曲线测试结果 Fig.4 Simulation results of function values 4 结束语 本文在研究蝙蝠算法优化机理的基础上,分析 了原有算法的局限性,基于近年来的研究发现,采用 Lévy 飞行策略来模拟蝙蝠搜索捕食行为,从本质上 提升了算法的优化性能,同时减少了算法参数.通过 标准函数的仿真测试表明,具有 Lévy 飞行特征的蝙 蝠算法有效改善了蝙蝠个体的寻优能力,收敛性能 和寻优精度有显著提高,适合于求解复杂函数优化 问题. 由于蝙蝠算法优化理论和应用研究还处于初始 阶段,许多问题还有待于人们不断地探索和解决,如 算法的鲁棒性和收敛性分析、算法参数设置的理论 依据以及与其他优化算法的有机融合等,这些都是 进一步要做的研究工作. 参考文献: [1]李晓磊,邵之江,钱积新.一种基于动物自治体的寻优模式: 鱼群算法[J].系统工程理论与实践, 2002, 22(11): 32⁃38. LI Xiaolei, SHAO Zhijiang, QIAN Jixin. An optimizing method based on autonomous animats: fish⁃swarm algorithm [J]. Systems Engineering—Theory & Practice, 2002, 22 (11): 32⁃38. [2]KARABOGA D. An idea based on honey bee swarm for nu⁃ merical optimization, Technical Report⁃TR06[R]. Kayseri, Turkey: Erciyes University, 2005. [ 3 ] YANG Xinshe. Nature⁃inspired metaheuristic algorithms [M]. Frome, UK: Luniver Press, 2008: 79⁃90. [4]KRISHNANAND K N, GHOSE D. Glowworm swarm optimi⁃ zation for simultaneous capture of multiple local optima of multimodal functions[J]. Swarm Intelligence, 2009, 3(2): 87⁃124. [5] YANG Xinshe. A new metaheuristic bat⁃inspired algorithm [M] / / GONZALEZ J R, PELTA D A. Nature Inspired Co⁃ 第 3 期 刘长平,等:具有 Lévy 飞行特征的蝙蝠算法 ·245·

·246· 智能系统学报 第8卷 operative Strategies for Optimization.Berlin:Springer-Ver- [15]SCHREIER A L,GROVE M.Ranging patterns of hamadr- lag,2010:65-74. yas baboons:random walk analyses[J].Animal Behavior, [6]LEMMA T A,HASHIM B M.Use of fuzzy systems and bat 2010.80(1):75-87. algorithm for exergy modeling in a gas turbine generator [16]HUMPHRIES N E,QUEIROZ N,DYER J R,et al.Envi- [C]//Proceedings of IEEE Colloquium on Humanities,Sci- ronmental context explains Levy and Brownian movement ence and Engineering.Penang,Malaysia,2011:305-310. patterns of marine predators[J].Nature,2010,465: [7]BORA T C,COELHO L S,LEBENSZTAJN L.Bat-inspired 1066-1069. optimization approach for the brushless DC wheel motor [17]BERTRAND S,BERTRAND A,GUEVARA-CARRASCO problem[J].IEEE Transactions on Magnetics,2012,48 R,et al.Scale-invariant movements of fishermen:the (2):947-950. same foraging strategy as natural predators[J.Ecological [8]VISWANATHAN G M,AFANASYEV V,BULDYREV S Applications,2007,17(2):331-337. V,et al.Levy flight search patterns of wandering albatros- [18]REYNOLDS A M.Cooperative random Levy flight searches ses[J].Nature,.1996,381:413-415. and the flight patterns of honeybees[J].Physics Letters A, [9]EDWARDS A M,PHILLIPS R A,WATKINS N W,et al.Re- 2006,354(5/6):384-388. visiting Levy flight search patterns of wandering albatrosses, [19]SHI Y,EBERHART R.A modified particle swarm optimi- bumblebees and deer[J].Nature,2007,449:1044-1048. zer[C]//Proceedings of IEEE International Conference on [10]REYNOLDS A M,SMITH A D,REYNOLDS D R,et al. Evolutionary Computation.Anchorage,USA,1998:69-73. Honeybees perform optimal scale-free searching flights 作者简介: when attempting to locate a food source[J].The Journal of 刘长平,男.1974年生,讲师.博士 Experimental Biology,2007,210(21):3763-3770. 研究生,主要研究方向为智能优化、管 [11]REYNOLDS A M,FRYE M A.Free-flight odor tracking in 理工程 drosophila is consistent with an optimal intermittent scale- free search[J].PLoS One,2007,2(4):1-9. [12]MARELL.A,BALL J P,HOFGAARD A.Foraging and movement paths of female reindeer:insights from fractal a- nalysis,correlated random walks,and Levy flights [J]. 叶春明,男,1964年生,教授.博士 Canadian Journal of Zoology,2002.80(5):854-865. 生导师,主要研究方向为智能优化、工 [13]RAMOS F G,MATEOS JL,MIRAMONTES O.Levy walk 业工程.主持国家自然科学基金项目、 patterns in the foraging movements of spider monkeys 科技部重大专项合作课题、教育部高校 (Ateles geoffroyi)[].Behavioral Ecology and Sociobiolo- 博士学科点专项科研基金项目、教育部 g,2004,55(3):1743-1750. 人文社会科学规划基金项目、上海市教 [14]AUSTIN D,BOWEN W D,MCMILLAN J I.Intraspecific 委科研创新重点项目多项.发表学术论文160余篇,其中被 variation in movement pattems:modeling individual behavior SCI、EI、ISTP检索30余篇. in a large marine predator[.Oikos,2004,105(1):15-30
operative Strategies for Optimization. Berlin: Springer⁃Ver⁃ lag, 2010: 65⁃74. [6]LEMMA T A, HASHIM B M. Use of fuzzy systems and bat algorithm for exergy modeling in a gas turbine generator [C] / / Proceedings of IEEE Colloquium on Humanities, Sci⁃ ence and Engineering. Penang, Malaysia, 2011: 305⁃310. [7]BORA T C, COELHO L S, LEBENSZTAJN L. Bat⁃inspired optimization approach for the brushless DC wheel motor problem[ J]. IEEE Transactions on Magnetics, 2012, 48 (2): 947⁃950. [8] VISWANATHAN G M, AFANASYEV V, BULDYREV S V, et al. Lévy flight search patterns of wandering albatros⁃ ses[J]. Nature, 1996, 381: 413⁃415. [9]EDWARDS A M, PHILLIPS R A, WATKINS N W, et al. Re⁃ visiting Lévy flight search patterns of wandering albatrosses, bumblebees and deer[J]. Nature, 2007, 449: 1044⁃1048. [10]REYNOLDS A M, SMITH A D, REYNOLDS D R, et al. Honeybees perform optimal scale⁃free searching flights when attempting to locate a food source[J]. The Journal of Experimental Biology, 2007, 210(21): 3763⁃3770. [11]REYNOLDS A M, FRYE M A. Free⁃flight odor tracking in drosophila is consistent with an optimal intermittent scale⁃ free search[J]. PLoS One, 2007, 2(4): 1⁃9. [12] MARELL A, BALL J P, HOFGAARD A. Foraging and movement paths of female reindeer: insights from fractal a⁃ nalysis, correlated random walks, and Lévy flights [ J]. Canadian Journal of Zoology, 2002, 80(5): 854⁃865. [13]RAMOS F G, MATEOS J L, MIRAMONTES O. Lévy walk patterns in the foraging movements of spider monkeys (Ateles geoffroyi)[J]. Behavioral Ecology and Sociobiolo⁃ gy, 2004, 55(3): 1743⁃1750. [14] AUSTIN D, BOWEN W D, MCMILLAN J I. Intraspecific variation in movement patterns: modeling individual behavior in a large marine predator[J]. Oikos, 2004, 105(1): 15⁃30. [15]SCHREIER A L, GROVE M. Ranging patterns of hamadr⁃ yas baboons: random walk analyses[J]. Animal Behavior, 2010, 80(1): 75⁃87. [16]HUMPHRIES N E, QUEIROZ N, DYER J R, et al. Envi⁃ ronmental context explains Lévy and Brownian movement patterns of marine predators [ J ]. Nature, 2010, 465: 1066⁃1069. [17]BERTRAND S, BERTRAND A, GUEVARA⁃CARRASCO R, et al. Scale⁃invariant movements of fishermen: the same foraging strategy as natural predators[ J]. Ecological Applications, 2007, 17(2): 331⁃337. [18]REYNOLDS A M. Cooperative random Lévy flight searches and the flight patterns of honeybees[J]. Physics Letters A, 2006, 354(5 / 6): 384⁃388. [19]SHI Y, EBERHART R. A modified particle swarm optimi⁃ zer[C] / / Proceedings of IEEE International Conference on Evolutionary Computation. Anchorage, USA, 1998: 69⁃73. 作者简介: 刘长平,男,1974 年生,讲师,博士 研究生,主要研究方向为智能优化、管 理工程. 叶春明,男,1964 年生,教授,博士 生导师,主要研究方向为智能优化、工 业工程.主持国家自然科学基金项目、 科技部重大专项合作课题、教育部高校 博士学科点专项科研基金项目、教育部 人文社会科学规划基金项目、上海市教 委科研创新重点项目多项.发表学术论文 160 余篇,其中被 SCI、EI、ISTP 检索 30 余篇. ·246· 智 能 系 统 学 报 第 8 卷