
第8卷第3期 智能系统学报 Vol.8 No.3 2013年6月 CAAI Transactions on Intelligent Systems Jun.2013 D0I:10.3969/i.issn.1673-4785.201210019 网络出版地址:http://www.cnki.net/kcms/detail/23.1538.TP.20130515.0836.001.html 采用Leader-follower和模糊反馈机制的 机器鱼队形控制 单素素,纪志坚,翟海川 (青岛大学自动化工程学院,山东青岛266071) 摘要:在Leader-follower框架下的多机器鱼系统队形控制中,针对Leader和Follower相对独立及落后机器鱼离队等 问题,在传统的Leader--follower队形控制算法中引入模糊反馈控制器进行反馈调节,使得领航机器鱼Leader能定时 检查Follower的位置,将多机器鱼系统的队形控制问题转化为具有反馈调节的Follower跟踪Leader的位置和方向的 问题,以增强多机器鱼队形控制的稳定性,更好地协同作业完成任务.仿真试验验证了所提出的方法能较好地实现多 机器鱼系统的队形控制: 关键词:多机器鱼系统:队形控制:Leader-follower:模糊反馈控制器:反馈调节:协同作业 中图分类号:TP242.6文献标志码:A文章编号:1673-4785(2013)03-0247-07 中文引用格式:单素素,纪志坚,翟海川.采用Leader--follower和模糊反馈机制的机器鱼队形控制[J].智能系统学报,2013,8(3): 247-253. 英文引用格式:SHAN Susu,JI Zhijian,ZHAI Haichuan.The formation control of multi-robot fish based on leader-follower and fuzzy feedback mechanism[J].CAAI Transactions on Intelligent Systems,2013,8(3):247-253. The formation control of multi-robot fish based on leader-follower and fuzzy feedback mechanism SHAN Susu,JI Zhijian,ZHAI Haichuan (College of Automation Engineering,Qingdao University,Qingdao 266071,China) Abstract:In the formation control of multi-robot fish under the leader-follower framework,the fuzzy feedback con- troller was introduced to traditional leader-follower formation control algorithm in efforts to cope with the relative in- dependence of the leader and followers,as well as the desertion of the laggard robot fishes.The goal was to ensure that the pilot robotic fish could check the position of followers regularly.In order to enhance the stability of the for- mation control of multi-robot fish and complete the task of collaborative operation,the formation control problem of multi-robot fish system was transformed into the problem of followers'tracking the position and orientation of the leader with the addition of the feedback regulation.Simulations verify that the proposed method can better realize the formation control of the robotic fish system. Keywords:multi-robot fish system;formation control;leader-follower;fuzzy feedback controller;feedback regula- tion;collaborative operation 在多机器鱼系统中协作是必不可少的,而机器 问题,是多机器鱼协作的基础).无论是从提升机器 鱼的队形控制则是一个具有典型性和通用性的协作 鱼的智能化水平还是从加快其实用化进程来说,多 机器鱼队形控制研究都有着及其重要的意义和价 收稿日期:2012-10-12.网络出版日期:2013-05-15. 值2 基金项目:国家自然科学基金资助项目(61075114,41076062). 多条机器鱼通过队形控制策略,能在某种环境 通信作者:纪志坚.E-mail:jizhijian@pku.og.cn
第 8 卷第 3 期 智 能 系 统 学 报 Vol.8 №.3 2013 年 6 月 CAAI Transactions on Intelligent Systems Jun. 2013 DOI:10.3969 / j.issn.1673⁃4785.201210019 网络出版地址:http: / / www.cnki.net / kcms/ detail / 23.1538.TP.20130515.0836.001.html 采用 Leader⁃follower 和模糊反馈机制的 机器鱼队形控制 单素素,纪志坚,翟海川 (青岛大学 自动化工程学院,山东 青岛 266071) 摘 要:在 Leader⁃follower 框架下的多机器鱼系统队形控制中,针对 Leader 和 Follower 相对独立及落后机器鱼离队等 问题,在传统的 Leader⁃follower 队形控制算法中引入模糊反馈控制器进行反馈调节,使得领航机器鱼 Leader 能定时 检查 Follower 的位置,将多机器鱼系统的队形控制问题转化为具有反馈调节的 Follower 跟踪 Leader 的位置和方向的 问题,以增强多机器鱼队形控制的稳定性,更好地协同作业完成任务.仿真试验验证了所提出的方法能较好地实现多 机器鱼系统的队形控制. 关键词:多机器鱼系统;队形控制;Leader⁃follower;模糊反馈控制器;反馈调节;协同作业 中图分类号:TP242.6 文献标志码:A 文章编号:1673⁃4785(2013)03⁃0247⁃07 中文引用格式:单素素,纪志坚,翟海川.采用 Leader⁃follower 和模糊反馈机制的机器鱼队形控制[ J].智能系统学报, 2013, 8( 3): 247⁃253. 英文引用格式:SHAN Susu, JI Zhijian, ZHAI Haichuan.The formation control of multi⁃robot fish based on leader⁃follower and fuzzy feedback mechanism[J]. CAAI Transactions on Intelligent Systems, 2013, 8(3): 247⁃253. The formation control of multi⁃robot fish based on leader⁃follower and fuzzy feedback mechanism SHAN Susu, JI Zhijian, ZHAI Haichuan (College of Automation Engineering, Qingdao University, Qingdao 266071, China) Abstract:In the formation control of multi⁃robot fish under the leader⁃follower framework, the fuzzy feedback con⁃ troller was introduced to traditional leader⁃follower formation control algorithm in efforts to cope with the relative in⁃ dependence of the leader and followers, as well as the desertion of the laggard robot fishes. The goal was to ensure that the pilot robotic fish could check the position of followers regularly. In order to enhance the stability of the for⁃ mation control of multi⁃robot fish and complete the task of collaborative operation, the formation control problem of multi⁃robot fish system was transformed into the problem of followers’ tracking the position and orientation of the leader with the addition of the feedback regulation. Simulations verify that the proposed method can better realize the formation control of the robotic fish system. Keywords: multi⁃robot fish system; formation control; leader⁃follower; fuzzy feedback controller; feedback regula⁃ tion; collaborative operation 收稿日期:2012⁃10⁃12. 网络出版日期:2013⁃05⁃15. 基金项目:国家自然科学基金资助项目(61075114,41076062). 通信作者:纪志坚. E⁃mail: jizhijian@ pku.org.cn. 在多机器鱼系统中协作是必不可少的,而机器 鱼的队形控制则是一个具有典型性和通用性的协作 问题,是多机器鱼协作的基础[1] .无论是从提升机器 鱼的智能化水平还是从加快其实用化进程来说,多 机器鱼队形控制研究都有着及其重要的意义和价 值[2⁃3] . 多条机器鱼通过队形控制策略,能在某种环境

·248· 智能系统学报 第8卷 约束下,始终保持一定的队形4)前进.这种策略一 状态,确保它必须向目标位置行进.构建Leader的运 般包含2个步骤:1)依据所处环境,确定各机器鱼 动模型6,如图1所示。 的目标位置:2)再由控制策略得到控制命令,机器 鱼在控制命令的约束下便能以一定的队形运行到目 Goal 标位置目前,大致有3种方法可以应用于机器鱼队 形控制,即Leader--follower算法[8】、基于行为算法列 和虚拟结构法[o.其中,Leader--follower算法是将队 形中的机器鱼划分为Leader和Follower2个角色, Follower的运行状态由Leader决定,进而实现队形 控制.这种控制方法比较简单,但因Leader与Follo- ver之间没有信息反馈,相对独立,在复杂环境中 图1 Leader的运动模型 Follower在跟踪过程中容易丢失[).一些文献中给出 Fig.I Movement model of Leader 了针对该算法缺点的解决方法,文献[11]应用精确 设定O点为机器鱼的参考原点,根据Leader的 反馈线性化方法设计控制器来确保编队的渐近稳 运动模型,并考虑机器鱼有效旋转半径d的影响,可 定.本文则是在Leader-follower算法的基础上引入模 得式(1)【6: 糊反馈控制器,使得Follower能够实时地将队形信 息通过模糊控制器反馈给Leader,确保Leader及时 dw,sin o-v,cos 调整自身运行状态,使落后或离队的Follower可以 v,sin dw,cos o (1) 9= -10 通过反馈调节作用重新回归队伍,以更好地实现队 r r 形控制。 式中:r为机器鱼参考原点与目标点的距离,”为机 器鱼中心线与目标点的夹角, 1基本的Leader-follower队形控制策略 控制的最终目标是使Leader到达目标点,即r= 由多条机器鱼组成一个群体中,一条机器鱼为 0,p=0.可以将控制策略定义为: Leader,其他的鱼均为Follower,各个Follower与 =-&r; Leader都有一定的相对位置关系,并同时跟踪Lead- (2) er的位置及方向[].Leader可以控制整个系统的运 9=-2P 动趋势,其状态由所有Follower共享[)],由此实现 式中:a,、α2是给定的比例系数,二者均为正数.将式 多机器鱼的队形控制. (1)、(2)联立可以解得控制变量为: 基本的Leader--follower队形控制策略还衍生出 a sin o a,ocos 很多扩展形式,比如单一Leader的l-p算法、多个 -r; reos o-d Leader的l-l算法以及跟踪链算法等.目前,基于 a(r-dcos o)+doa sin Leader-follower队形控制中多采用l-p控制方法[) rcos o-d 而编队队形中按跟踪的拓扑结构,又可分为串联编 考虑到(vs,0)的限制,控制变量应为: 队和并联编队.在串联编队结构中,每个Follower根 据与它相邻近的机器鱼来确定自己的位置:并联编 0,=了0, 一10ms≤10,≤0mx; 队结构中,Follower则是根据Leader的位置去确定 -10 tmas 0,<一Wm 自身位置.文献[15]对比分析了这2种拓扑结构的 Vt Uimaxi 稳定性,在群体中只存在单一Leader时,并联编队 v,=301, 一Umx≤飞,≤Vms; 的稳定度要优于串联编队.在本文中,采用并联结构 来对机器鱼进行控制. -Vma,U <-Vimas" 1.2 队形保持 l.1 Leader向目标点运行 本文采用l-p控制的方法来保持队形.它是 在Leader-follower队形控制策略中,Leader作 通过控制2条机器鱼之间的相对距离!和相对角度 为这个队形的参照物,对整个队列能否准确运行到 p,使之达到一对理想值(L4,P),从而形成和保持一 目标位置起决定作用.在这里先分析Leader的运行 个良好的编队队形,如图2所示
约束下,始终保持一定的队形[4⁃7] 前进.这种策略一 般包含 2 个步骤:1) 依据所处环境,确定各机器鱼 的目标位置;2) 再由控制策略得到控制命令,机器 鱼在控制命令的约束下便能以一定的队形运行到目 标位置.目前,大致有 3 种方法可以应用于机器鱼队 形控制,即 Leader⁃follower 算法[8] 、基于行为算法[9] 和虚拟结构法[10] .其中,Leader⁃follower 算法是将队 形中的机器鱼划分为 Leader 和 Follower 2 个角色, Follower 的运行状态由 Leader 决定,进而实现队形 控制.这种控制方法比较简单,但因 Leader 与 Follo⁃ wer 之间没有信息反馈,相对独立,在复杂环境中 Follower 在跟踪过程中容易丢失[8] .一些文献中给出 了针对该算法缺点的解决方法,文献[11]应用精确 反馈线性化方法设计控制器来确保编队的渐近稳 定.本文则是在 Leader⁃follower 算法的基础上引入模 糊反馈控制器,使得 Follower 能够实时地将队形信 息通过模糊控制器反馈给 Leader,确保 Leader 及时 调整自身运行状态,使落后或离队的 Follower 可以 通过反馈调节作用重新回归队伍,以更好地实现队 形控制. 1 基本的 Leader⁃follower 队形控制策略 由多条机器鱼组成一个群体中,一条机器鱼为 Leader,其 他 的 鱼 均 为 Follower, 各 个 Follower 与 Leader 都有一定的相对位置关系,并同时跟踪 Lead⁃ er 的位置及方向[12] .Leader 可以控制整个系统的运 动趋势,其状态由所有 Follower 共享[13] ,由此实现 多机器鱼的队形控制. 基本的 Leader⁃follower 队形控制策略还衍生出 很多扩展形式,比如单一 Leader 的 l⁃φ 算法、多个 Leader 的 l⁃l 算法以及跟踪链算法等. 目前,基于 Leader⁃follower 队形控制中多采用 l⁃φ 控制方法[14] . 而编队队形中按跟踪的拓扑结构,又可分为串联编 队和并联编队.在串联编队结构中,每个 Follower 根 据与它相邻近的机器鱼来确定自己的位置;并联编 队结构中,Follower 则是根据 Leader 的位置去确定 自身位置.文献[15]对比分析了这 2 种拓扑结构的 稳定性,在群体中只存在单一 Leader 时,并联编队 的稳定度要优于串联编队.在本文中,采用并联结构 来对机器鱼进行控制. 1.1 Leader 向目标点运行 在 Leader⁃follower 队形控制策略中, Leader 作 为这个队形的参照物,对整个队列能否准确运行到 目标位置起决定作用.在这里先分析 Leader 的运行 状态,确保它必须向目标位置行进.构建 Leader 的运 动模型[16] ,如图 1 所示. 图 1 Leader 的运动模型 Fig.1 Movement model of Leader 设定 O 点为机器鱼的参考原点,根据 Leader 的 运动模型,并考虑机器鱼有效旋转半径 d 的影响,可 得式(1) [16] : r · = dwt sin φ - vt cos φ; φ · = vt sin φ r + dwt cos φ r - wt . ì î í ï ï ï ï (1) 式中:r 为机器鱼参考原点与目标点的距离,φ 为机 器鱼中心线与目标点的夹角. 控制的最终目标是使 Leader 到达目标点,即r = 0,φ= 0.可以将控制策略定义为: r · = - α1 r; φ · = - α2φ. ì î í ïï ïï (2) 式中:α1 、α2 是给定的比例系数,二者均为正数.将式 (1)、(2)联立可以解得控制变量为: wt = α1 sin φ + α2φcos φ rcos φ - d r; vt = α1 (r - dcos φ) + dφα2 sin φ rcos φ - d r. ì î í ï ïï ï ï 考虑到(vtmax,wtmax)的限制,控制变量应为: wt = wtmax, wt, - wtmax, ì î í ï ï ï ï wt > wtmax; - wtmax ≤ wt ≤ wtmax; wt < - wtmax . vt = vtmax, vt, - vtmax, ì î í ï ï ï ï vt > vtmax; - vtmax ≤ vt ≤ vtmax; vt < - vtmax . 1.2 队形保持 本文采用 l⁃φ 控制的方法[14] 来保持队形.它是 通过控制 2 条机器鱼之间的相对距离 l 和相对角度 φ,使之达到一对理想值(l d ,φd ),从而形成和保持一 个良好的编队队形,如图 2 所示. ·248· 智 能 系 统 学 报 第 8 卷

第3期 单素素,等:采用Leader-follower和模糊反馈机制的机器鱼队形控制 ·249· 一ma≤,≤t书ms; 1Umm; 高队形保持率.当个别机器鱼有离队现象时,Leader 10,= -0mx≤10,≤0mx; 开始低速前进,同时离队的Follower开始高速前进, 10,<一10mx 使得落后的机器鱼能够回归队伍,防止Follower掉
图 2 基于 l⁃φ 的队形保持 Fig.2 Formation keeping based on l⁃φ 下面以一个由 2 条机器鱼组成的系统为例,给 出该算法的详细说明.在控制过程中,领航机器鱼 Leader 的状态表示为 R0(x0 ,y0 ,v0 ,w0 ),跟随机器鱼 Follower 的状态表示为 Rt(xt,yt,vt,wt),机器鱼线速 度的正方向为机器鱼前行的方向,角速度的正方向 为逆时针方向.根据队形要求,Follower 相对于 Lead⁃ er 的 相 对 参 数 为 ( l, φ), 如 图 2 所 示, 可 得 式 (3) [16] : l · = vt cos r - dwt sin r - v0 cos φ + dw0 sin φ; φ · = 1 l (v0 sin φ + dw0 cos φ - vt sin r - dwt cos r - lw0). ì î í ï ï ï ï (3) 式中:w0 、wt 分别为 Leader 和 Follower 的角速度,θ0 、 θt 分别为 Leader 和 Follower 运动方向与正 x 轴的夹 角,由几何知识可知 r = φ+θ0 -θt,l d 、φd 分别为队形 要求中 Follower 相对于 Leader 的理想距离和方位 角.为使 2 条机器鱼保持一定的队形,控制的最终目 标为(l-l d )→0,(φ-φd )→0.将控制策略定义为: l · = β1(l d - l); φ · = β2(φd - φ). ì î í ïï ï (4) 将式(3)、(4)联立可解得控制变量为: wt = - cos r d [β2 l(φd - φ) - v0 sin φ - dw0 cos φ + lw0 + ρsin r]; vt = ρ + dwt tan r. ì î í ï ï ï ï 式中:ρ = β1(l d -l)+v0 cos φ-dw0 sin φ cos r . 同样,考虑到( vtmax,wtmax ) 的限制,控制变量应 变为: wt = wtmax, wt, - wtmax, ì î í ï ï ïï wt > wtmax; - wtmax ≤ wt ≤ wtmax; wt < - wtmax . vt = vtmax, vt, - vtmax, ì î í ï ï ïï vt > vtmax; - vtmax ≤ vt ≤ vtmax; vt < - vtmax . 由此可以看出,在 l⁃φ 算法中,只要给定领航机 器鱼的角速度、线速度、位置和航向,跟随者就可以 保证向着与领航机器鱼相对距离为 l 和相对方向为 φ 的位置移动,实现队形的保持. 2 基于 Leader⁃follower 算法引入反馈 调节的多机器鱼队形控制 2.1 基本思想 在传统的 Leader⁃follower 算法中,机器鱼系统 的队形控制简单且稳定,但 Leader 和 Follower 相对 独立,在复杂环境中易出现离队现象.本文在保留 Leader⁃follower 算法优点的基础上引入反馈环节,使 机器鱼队伍在复杂环境中能更好地保持队形并避开 障碍物,多机器鱼的队形控制更加有效.具有反馈调 节的队形控制结构如图 3 所示. 图 3 具有反馈调节的 Leader⁃follower 队形控制结构 Fig.3 Leader⁃follower formation control structure with feedback regulation 2.2 基本原理 本文设计的具有反馈调节的 Leader⁃follower 队 形控制的基本原理如下: 1)开始时 Leader 接受任务 T,然后根据外界环 境 E 规划运动路径,并将自身的运行状态 R0(x0 ,y0 , v0 ,w0 )发送给每个 Follower. 2)每个 Follower 根据接收到的信息计算自己在 队形中的相对位置 pi = (xi,yi)(i = 1,2,…,n),结合 外界环境 E,根据队形控制策略产生控制变量,即 (vi,wi). 3)队形信息 P = (p1 ,p2 ,…,pn )通过模糊控制器 反馈给 Leader,其中 p1 为 Follower(1) 的相对位置. 正常运行时 Leader 不将队形反馈信息作为自己运 行的依据,仅依靠 Follower 自身调整运行状态来提 高队形保持率.当个别机器鱼有离队现象时,Leader 开始低速前进,同时离队的 Follower 开始高速前进, 使得落后的机器鱼能够回归队伍,防止 Follower 掉 第 3 期 单素素,等:采用 Leader⁃follower 和模糊反馈机制的机器鱼队形控制 ·249·
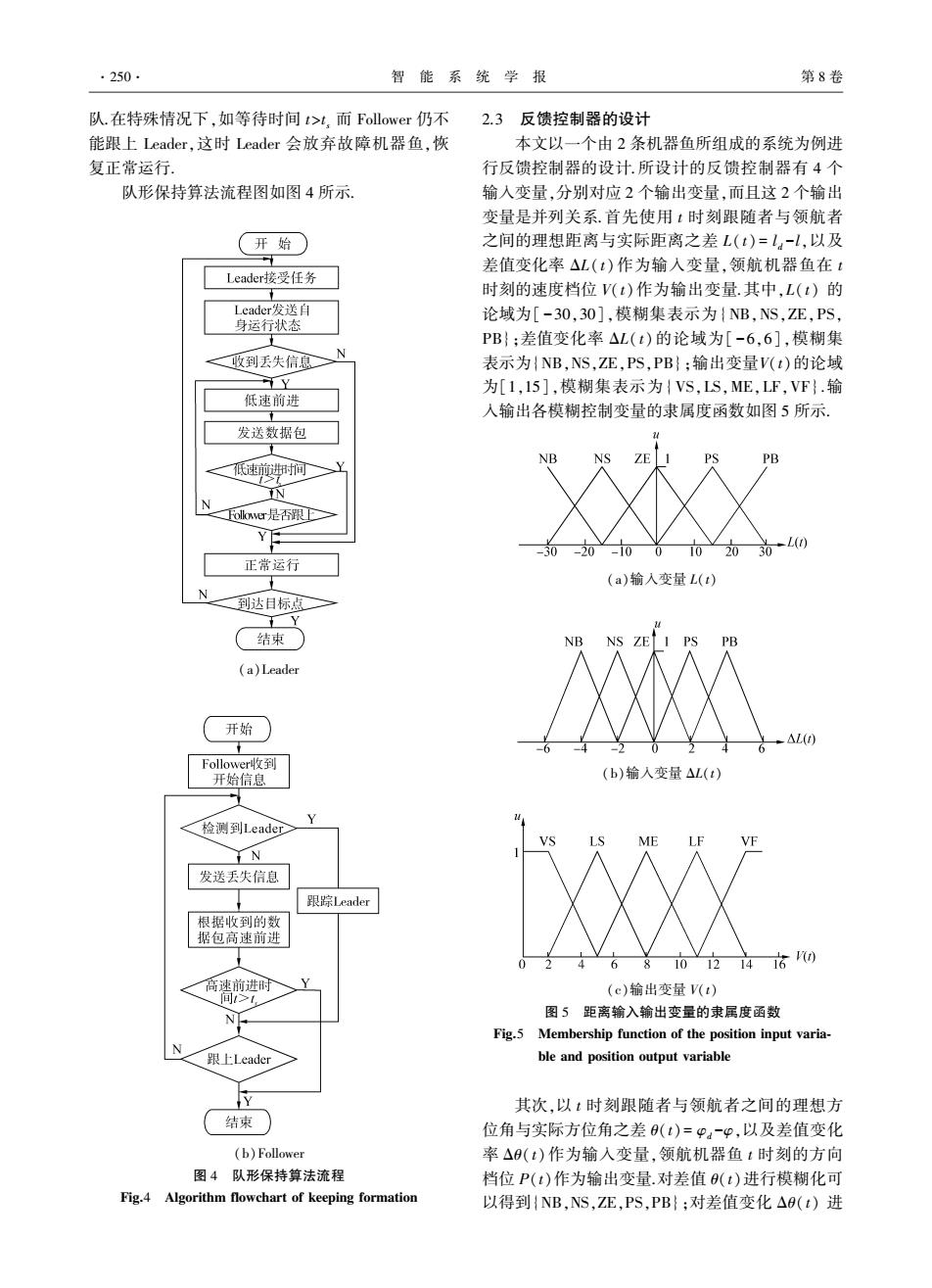
.250. 智能系统学报 第8卷 队.在特殊情况下,如等待时间t>t,而Follower仍不 2.3反馈控制器的设计 能跟上Leader,这时Leader会放弃故障机器鱼,恢 本文以一个由2条机器鱼所组成的系统为例进 复正常运行 行反馈控制器的设计.所设计的反馈控制器有4个 队形保持算法流程图如图4所示. 输入变量,分别对应2个输出变量,而且这2个输出 变量是并列关系.首先使用1时刻跟随者与领航者 (开始 之间的理想距离与实际距离之差L(t)=L-L,以及 差值变化率△L(t)作为输人变量,领航机器鱼在t Leader接受任务 时刻的速度档位V(t)作为输出变量.其中,L(t)的 Leader发送自 论域为[-30,30],模糊集表示为{NB,NS,ZE,PS, 身运行状态 PB}:差值变化率△L(t)的论域为[-6,6],模糊集 N 收到丢失信息 表示为{NB,NS,ZE,PS,PB};输出变量V(t)的论域 高Y 为[1,15],模糊集表示为{VS,LS,ME,LF,VF}.输 低速前进 入输出各模糊控制变量的隶属度函数如图5所示. 发送数据包 NB NS ze PB 低速前时间 N N Olwe是否跟E Y后 -30-20-100 102030L(0 正常运行 (a)输入变量L(t) N 到达日标点一 Y (结束) NB NS ZE1 PS PB (a)Leader 开始 △L(t) Followert收到 开始信息 (b)输入变量△L(t) 检测到Leader Y VS ME VE TN 发送丢失信息 跟踪Leader 根据收到的数 据包高速前进 6 81012460 高速前进时 (c)输出变量V(t) 间>1, 图5距离输入输出变量的隶属度函数 Fig.5 Membership function of the position input varia- N 跟上Leader ble and position output variable 其次,以t时刻跟随者与领航者之间的理想方 结束 位角与实际方位角之差(t)=P。-p,以及差值变化 (b)Follower 率△(t)作为输入变量,领航机器鱼t时刻的方向 图4队形保持算法流程 档位P(t)作为输出变量.对差值(t)进行模糊化可 Fig.4 Algorithm flowchart of keeping formation 以得到{NB,NS,ZE,PS,PB}:对差值变化△(t)进
队.在特殊情况下,如等待时间 t>t s 而 Follower 仍不 能跟上 Leader,这时 Leader 会放弃故障机器鱼,恢 复正常运行. 队形保持算法流程图如图 4 所示. (a)Leader (b)Follower 图 4 队形保持算法流程 Fig.4 Algorithm flowchart of keeping formation 2.3 反馈控制器的设计 本文以一个由 2 条机器鱼所组成的系统为例进 行反馈控制器的设计.所设计的反馈控制器有 4 个 输入变量,分别对应 2 个输出变量,而且这 2 个输出 变量是并列关系.首先使用 t 时刻跟随者与领航者 之间的理想距离与实际距离之差 L( t) = l d -l,以及 差值变化率 ΔL( t) 作为输入变量,领航机器鱼在 t 时刻的速度档位 V(t)作为输出变量.其中,L( t) 的 论域为[ -30,30],模糊集表示为{NB,NS,ZE,PS, PB};差值变化率 ΔL( t) 的论域为[ -6,6],模糊集 表示为{NB,NS,ZE,PS,PB};输出变量V(t)的论域 为[1,15],模糊集表示为{VS,LS,ME,LF,VF}.输 入输出各模糊控制变量的隶属度函数如图 5 所示. (a)输入变量 L(t) (b)输入变量 ΔL(t) (c)输出变量 V(t) 图 5 距离输入输出变量的隶属度函数 Fig.5 Membership function of the position input varia⁃ ble and position output variable 其次,以 t 时刻跟随者与领航者之间的理想方 位角与实际方位角之差 θ(t)= φd -φ,以及差值变化 率 Δθ( t)作为输入变量,领航机器鱼 t 时刻的方向 档位 P(t)作为输出变量.对差值 θ(t)进行模糊化可 以得到{NB,NS,ZE,PS,PB};对差值变化 Δθ(t) 进 ·250· 智 能 系 统 学 报 第 8 卷

第3期 单素素,等:采用Leader-follower和模糊反馈机制的机器鱼队形控制 ·251- 行模糊化可得{NB,NS,ZE,PS,PB}:输出变量P(t) 表1机器鱼速度档位控制规则表 的论域为[-7,7],其模糊集为{LB,LS,ME,S, Table 1 Speed stalls control rule table of multi-robot fish RB}.输入输出各模糊控制变量的隶属度函数如图6 V(1) 所示 AL(t)L(t)=L(t)=L(1)= L(t)=L(t)= NB NS ZE PS PB NB VS VS VS ME LF NB NS ZE PS PB NS VS VS LS ME LF ZE LS LS ME LF LF PS LS ME LF VE VF PB LS ME VE VE VE 表2机器鱼方向档位控制规则表 -60 -15 Table 2 Direction stalls control rule table of multi-robot fish (a)输入变量0(t) P(t) △0(t)0(t)=0(t)= (t)=0(t)=0(t)= nB NS ZE PS PB NB LB LB LS me RS NB ZE PS PB NS LB LB LS ME RS ZE LB LS ME RS RB PS LS ME RS RB RB PB LS ME RS RB RB -10-5 0 5 75440 3仿真实验与分析 (b)输入变量△9(t) 在实验仿真过程中,以2条机器鱼在复杂环境 中保持一定队形,并运动到指定位置为目标.首先 Leader根据环境信息自主规划运动路径,并将自身 LB LS 1ME RS RB 的状态信息传递给各个Follower.然后每个Follower 分别计算自己在队形中的位置并将自身的信息反馈 给Leader.最终在正常运行状态下,Leader不受队形 反馈信息的影响,队形仅依靠Follower自行调整速 度和方位角来保持. P(n 利用MATLAB工具,根据各控制变量的隶属度 (c)输出变量P(t) 函数及模糊规则建立模糊反馈控制器,并将其导入 图6方位角输入输出变量的隶属度函数 到Simulink工作区,搭建出反馈控制环节.实验中, Fig.6 Membership function of the orientation input 在5s时加入扰动,使Follower与Leader之间的距离 variable and orientation output variable 和方位角均偏离理想值:在10s时加入扰动仅使距 离偏离理想值:在12s时再次加入扰动仅使方位角 由于模糊控制器的2个输出变量是并列关系, 偏离理想值.得到Leader的速度档位和方向档位波 因此需要建立2个并列的规则库,其模糊推理规则 形图如图7所示. 可以分别表示为: 15 If L(t)and AL(t),then V(t) If 0(t)and 0(t)then P(t). 10 经过多次试验后,可以得到相应的模糊控制规 则表,如表1和2所示.在经过模糊化和模糊推理建 立模糊规则后,基于最大隶属度法,将得到的输出变 量进行清晰化.这样就可以得到精确的速度档位和 10 15 20 方向档位值,即领航机器鱼为了更好地保持队形即 t/s 将执行的2个游动指令. (a)速度档位
行模糊化可得{NB,NS,ZE,PS,PB};输出变量 P(t) 的论域为[ - 7,7],其模糊集为{ LB, LS,ME,RS, RB}.输入输出各模糊控制变量的隶属度函数如图 6 所示. (a)输入变量 θ(t) (b)输入变量 Δθ(t) (c)输出变量 P(t) 图 6 方位角输入输出变量的隶属度函数 Fig. 6 Membership function of the orientation input variable and orientation output variable 由于模糊控制器的 2 个输出变量是并列关系, 因此需要建立 2 个并列的规则库,其模糊推理规则 可以分别表示为: If L(t) and ΔL(t),then V(t) ; If θ(t) and Δθ(t),then P(t) . 经过多次试验后,可以得到相应的模糊控制规 则表,如表 1 和 2 所示.在经过模糊化和模糊推理建 立模糊规则后,基于最大隶属度法,将得到的输出变 量进行清晰化.这样就可以得到精确的速度档位和 方向档位值,即领航机器鱼为了更好地保持队形即 将执行的 2 个游动指令. 表 1 机器鱼速度档位控制规则表 Table 1 Speed stalls control rule table of multi⁃robot fish ΔL(t) V(t) L(t)= NB L(t)= NS L(t)= ZE L(t)= PS L(t)= PB NB VS VS VS ME LF NS VS VS LS ME LF ZE LS LS ME LF LF PS LS ME LF VF VF PB LS ME VF VF VF 表 2 机器鱼方向档位控制规则表 Table 2 Direction stalls control rule table of multi⁃robot fish Δθ(t) P(t) θ(t)= NB θ(t)= NS θ(t)= ZE θ(t)= PS θ(t)= PB NB LB LB LS ME RS NS LB LB LS ME RS ZE LB LS ME RS RB PS LS ME RS RB RB PB LS ME RS RB RB 3 仿真实验与分析 在实验仿真过程中,以 2 条机器鱼在复杂环境 中保持一定队形,并运动到指定位置为目标.首先 Leader 根据环境信息自主规划运动路径,并将自身 的状态信息传递给各个 Follower.然后每个 Follower 分别计算自己在队形中的位置并将自身的信息反馈 给 Leader.最终在正常运行状态下,Leader 不受队形 反馈信息的影响,队形仅依靠 Follower 自行调整速 度和方位角来保持. 利用 MATLAB 工具,根据各控制变量的隶属度 函数及模糊规则建立模糊反馈控制器,并将其导入 到 Simulink 工作区,搭建出反馈控制环节.实验中, 在5 s时加入扰动,使 Follower 与 Leader 之间的距离 和方位角均偏离理想值;在 10 s 时加入扰动仅使距 离偏离理想值;在 12 s 时再次加入扰动仅使方位角 偏离理想值.得到 Leader 的速度档位和方向档位波 形图如图 7 所示. (a)速度档位 第 3 期 单素素,等:采用 Leader⁃follower 和模糊反馈机制的机器鱼队形控制 ·251·

·252· 智能系统学报 第8卷 鱼实现编队控制,更好地完成协作任务具有非常重 要的意义。 参考文献: [1]谭民,范永,徐国华机器人群体协作与控制的研究[J刀 机器人,2001,23(2):178-182. TAN Min,FAN Yong,XU Guohua.Research on control 10 15 20 and cooperation for swarm robot systems[].Robot,2001, t/s 23(2):178-182 (b)方向档位 [2]SFAKIOTAKIS M,LANE D M,DAVIES J B C.Review of 图7 Leader的速度档位和方向档位 fish swimming modes for aquatic locomotion[].IEEE Jour- Fig.7 Speed and direction stalls of the leader nal of Oceanic Engineering,1999,24(2):237-252. 「3]刘军考,陈在礼,陈维山,等.水下机器人新型仿鱼鳍推 从仿真结果可以看出,当Follower与Leader之 进器[J].机器人,2000,22(5):427-432. 间的距离或方位角偏离理想值时,在反馈调节作用 LIU Junkao,CHEN Zaili,CHEN Weishan,et al.A new 下Leader在速度和方向档位上均能及时作出响应, type of underwater turbine imitating fish-fin for underwater 使整个队形尽快恢复到正常运行状态, obot[J].Robot,2000,22(5):427-432. [4]BEARD R W,LAWTON J,HADAEGH F Y.A coordina- 根据基于Leader-follower队形控制的基本原理及 tion architecture for spacecraft formation control[J].IEEE 算法流程图编写m文件,并在m文件中调用Simulink Transactions on Control Systems Technology,2001,9(6): 中搭建的反馈调节模块.多机器鱼系统加入反馈调节后 777-790. 的队形控制仿真结果如图8所示仿真结果表明多机器 [5]YAMAGUCHI H,BURDICK J W.Asymptotic stabilization 鱼系统在复杂环境下实现了队形控制,没有出现落后 of multiple nonholonomic mobile robots forming group forma- 机器鱼离队和死锁等问题 tions[C]//Proceedings of the 1998 IEEE International Con- ference on Robotics and Automation.Leuven,Belgium, 100 1998:3573-3580. [6]TANNER H G.PAPPAS G J.KUMAR V.Leader to forma- tion stability[J].IEEE Transactions on Robotics and Auto- mation,2004,20(3):443-455. Follower [7]DAS A K,FIERRO R,KUMAR V,et al.A vision-based eader formation control framework[J].IEEE Transactions on Ro- botics and Automation,2002,18(5):813-825. [8]WANG PK C.Navigation strategies for multiple autonomous -100 -50 0 50 100 mobile robots moving in formation[J].Journal of Robotic x/cm Systems,1991,8(2):177-195. 图8基于Leader-follower的多机器鱼系统队形控制仿真 [9]KUPPAN CHETTY R M.SINGAPERUMAL M,NAGARA- Fig.8 Formation control simulation figure of multi-robot JANT.Behavior based multi robot formations with active ob- fish system based on the leader-follower stacle avoidance based on switching control strategy[J].Ad- 4结束语 vanced Materials Research,2012,433-440:6630-6635. [10]任德华,卢桂章.对队形控制的思考[J].控制与决策, 本文以机器鱼系统为研究对象,在Leader-follo- 2005,20(6):601-606. wer算法的基础上引入模糊反馈控制器,使得领航 REN Dehua,LU Guizhang.Thinking in formation control 机器鱼Leader能定时检查Follower的位置,保证落 [J].Control and Decision,2005,20(6):601-606. [ll]张金学,掌明.非完整机器人Leader--follower编队控制器 后和离队的Follower相应地调整自身的运行状态顺 设计[J].智能计算机与应用,2011(4):20-22. 利归队.由仿真结果可以看出,采用Leader-follower ZHANG Jinxue,ZHANG Ming.Design of Leader-follower 和模糊反馈机制相结合的策略对机器鱼进行队形控 formation controller for nonholonomic mobile robots[].In- 制效果良好,既实现了多机器鱼系统的队形保持,又 telligent Computer and Applications,2011(4):20-22. 保证了队形运动的流畅性这些研究成果对于多机 「12]张磊.多智能体机器人系统设计与编队问题的研究 器鱼系统后续的研究起着积极的促进作用,对机器 [D].武汉:华中科技大学,2005:6-12
(b)方向档位 图 7 Leader 的速度档位和方向档位 Fig.7 Speed and direction stalls of the leader 从仿真结果可以看出,当 Follower 与 Leader 之 间的距离或方位角偏离理想值时,在反馈调节作用 下 Leader 在速度和方向档位上均能及时作出响应, 使整个队形尽快恢复到正常运行状态. 根据基于 Leader⁃follower 队形控制的基本原理及 算法流程图编写 m 文件,并在 m 文件中调用 Simulink 中搭建的反馈调节模块.多机器鱼系统加入反馈调节后 的队形控制仿真结果如图 8 所示.仿真结果表明多机器 鱼系统在复杂环境下实现了队形控制,没有出现落后 机器鱼离队和死锁等问题. 图 8 基于 Leader⁃follower 的多机器鱼系统队形控制仿真 Fig.8 Formation control simulation figure of multi⁃robot fish system based on the leader⁃follower 4 结束语 本文以机器鱼系统为研究对象,在 Leader⁃follo⁃ wer 算法的基础上引入模糊反馈控制器,使得领航 机器鱼 Leader 能定时检查 Follower 的位置,保证落 后和离队的 Follower 相应地调整自身的运行状态顺 利归队.由仿真结果可以看出,采用 Leader⁃follower 和模糊反馈机制相结合的策略对机器鱼进行队形控 制效果良好,既实现了多机器鱼系统的队形保持,又 保证了队形运动的流畅性.这些研究成果对于多机 器鱼系统后续的研究起着积极的促进作用,对机器 鱼实现编队控制,更好地完成协作任务具有非常重 要的意义. 参考文献: [1]谭民,范永,徐国华.机器人群体协作与控制的研究[ J]. 机器人, 2001, 23(2): 178⁃182. TAN Min, FAN Yong, XU Guohua. Research on control and cooperation for swarm robot systems[ J]. Robot, 2001, 23(2): 178⁃182. [2]SFAKIOTAKIS M, LANE D M, DAVIES J B C. Review of fish swimming modes for aquatic locomotion[J]. IEEE Jour⁃ nal of Oceanic Engineering, 1999, 24(2): 237⁃252. [3]刘军考,陈在礼,陈维山,等. 水下机器人新型仿鱼鳍推 进器[J].机器人, 2000, 22(5): 427⁃432. LIU Junkao, CHEN Zaili, CHEN Weishan, et al. A new type of underwater turbine imitating fish⁃fin for underwater robot[J]. Robot, 2000, 22(5): 427⁃432. [4]BEARD R W, LAWTON J, HADAEGH F Y. A coordina⁃ tion architecture for spacecraft formation control[ J]. IEEE Transactions on Control Systems Technology, 2001, 9(6): 777⁃790. [5]YAMAGUCHI H, BURDICK J W. Asymptotic stabilization of multiple nonholonomic mobile robots forming group forma⁃ tions[C] / / Proceedings of the 1998 IEEE International Con⁃ ference on Robotics and Automation. Leuven, Belgium, 1998: 3573⁃3580. [6]TANNER H G, PAPPAS G J, KUMAR V. Leader to forma⁃ tion stability[J]. IEEE Transactions on Robotics and Auto⁃ mation, 2004, 20(3): 443⁃455. [7]DAS A K, FIERRO R, KUMAR V, et al. A vision⁃based formation control framework[ J]. IEEE Transactions on Ro⁃ botics and Automation, 2002, 18(5): 813⁃825. [8]WANG P K C. Navigation strategies for multiple autonomous mobile robots moving in formation [ J]. Journal of Robotic Systems, 1991, 8(2): 177⁃195. [9]KUPPAN CHETTY R M, SINGAPERUMAL M, NAGARA⁃ JAN T. Behavior based multi robot formations with active ob⁃ stacle avoidance based on switching control strategy[J]. Ad⁃ vanced Materials Research, 2012, 433⁃440: 6630⁃6635. [10]任德华,卢桂章.对队形控制的思考[ J].控制与决策, 2005, 20(6): 601⁃606. REN Dehua, LU Guizhang. Thinking in formation control [J]. Control and Decision, 2005, 20(6): 601⁃606. [11]张金学,掌明.非完整机器人 Leader⁃follower 编队控制器 设计[J].智能计算机与应用, 2011(4): 20⁃22. ZHANG Jinxue, ZHANG Ming. Design of Leader⁃follower formation controller for nonholonomic mobile robots[J]. In⁃ telligent Computer and Applications, 2011(4): 20⁃22. [12]张磊. 多智能体机器人系统设计与编队问题的研究 [D].武汉: 华中科技大学, 2005: 6⁃12. ·252· 智 能 系 统 学 报 第 8 卷

第3期 单素素,等:采用Leader--follower和模糊反馈机制的机器鱼队形控制 ·253· ZHANG Lei.Research on multi-agent robots system and 作者简介: formation control[D].Wuhan:Huazhong University of 单素素,女,1988年生,硕士研究 Science and Technology,2005:6-12. 生,主要研究方向为多智能体系统 [l3]丁磊,郭戈.一种船队编队控制的backstepping方法[J]. 控制与决策,2009,27(2):299-303. DING Lei,GUO Ge.Formation control for ship fleet based on backstepping[J].Control and Decision,2009,27(2): 299-303. [14]DESAI J P,OSTROWSKI J,KUMAR V.Controlling for- 纪志坚,男,1973年生,教授,博土 mations of multiple mobile robots[C]//Proceedings of the 生导师,博士,主要研究方向为群体系 1998 IEEE International Conference on Robotics and Auto- 统动力学与协调控制、复杂网络、切换 mation.Leuven,Belgium,1998:2864-2869. 动力系统的分析与控制、系统生物以及 [15]程磊.多移动机器人协调控制系统的研究与实现[D]. 基于网络的控制系统等.先后主持国家 武汉:华中科技大学,2005:37-42. 自然科学基金2项,参与国家自然科学 CHENG Lei.Research and implementation on multiple mo- 基金及国家“973”和“863”计划项目多项.发表学术论文40 bile robots coordination control system[D].Wuhan:Hua- 余篇,其中被SCI检索16篇、I检索30余篇. zhong University of Science and Technology,2005:37-42. [16]董胜龙,陈卫东,席裕庚.多移动机器人编队的分布式控 翟海川,男,1988年生,硕士研究 制系统[J].机器人,2000.22(6):433-438 生,主要研究方向为多智能体系统 DONG Shenglong,CHEN Weidong,XI Yugeng.An dis- tributed control system for multi-mobile robots formation [J1].Robot,2000,22(6):433-438. 第14届EEE国际计算智能信息研讨会 14th IEEE International Symposium on Computational Intelligence and Informatics Authors are welcome to submit original and unpublished papers and attend the 14th IEEE International Symposium on Computational Intelligence and Informatics to be held on November 19-21,2013 in Budapest,Hungary. The Symposium is organized with the focus of bringing together scientists from any country working on computational intel- ligence and its applications with the aims at providing an opportunity for sharing and discussing the recent research devel- opments in this field.The idea is to have a small number of lecturers and participants in a relaxed and informal atmos- phere. Author's Schedule Full paper submission:August 12,2013 Notification:September 9,2013 Final manuscript submission:October 7,2013 Contact Secretary Aniko Szaka Obuda University E-mail:szakal@uni-obuda.hu Website:http://conf.uni-obuda.hu/cinti2013/index.html
ZHANG Lei. Research on multi⁃agent robots system and formation control [ D]. Wuhan: Huazhong University of Science and Technology, 2005: 6⁃12. [13]丁磊,郭戈.一种船队编队控制的 backstepping 方法[ J]. 控制与决策, 2009, 27(2): 299⁃303. DING Lei, GUO Ge. Formation control for ship fleet based on backstepping[J]. Control and Decision, 2009, 27(2): 299⁃303. [14]DESAI J P, OSTROWSKI J, KUMAR V. Controlling for⁃ mations of multiple mobile robots[C] / / Proceedings of the 1998 IEEE International Conference on Robotics and Auto⁃ mation. Leuven, Belgium, 1998: 2864⁃2869. [15]程磊.多移动机器人协调控制系统的研究与实现[D]. 武汉: 华中科技大学, 2005: 37⁃42. CHENG Lei. Research and implementation on multiple mo⁃ bile robots coordination control system[D]. Wuhan: Hua⁃ zhong University of Science and Technology, 2005: 37⁃42. [16]董胜龙,陈卫东,席裕庚.多移动机器人编队的分布式控 制系统[J].机器人, 2000, 22(6): 433⁃438. DONG Shenglong, CHEN Weidong, XI Yugeng. An dis⁃ tributed control system for multi⁃mobile robots formation [J]. Robot, 2000, 22(6): 433⁃438. 作者简介: 单素素,女,1988 年生,硕士研究 生,主要研究方向为多智能体系统. 纪志坚,男,1973 年生,教授,博士 生导师,博士,主要研究方向为群体系 统动力学与协调控制、复杂网络、切换 动力系统的分析与控制、系统生物以及 基于网络的控制系统等.先后主持国家 自然科学基金 2 项,参与国家自然科学 基金及国家“973”和“863”计划项目多项.发表学术论文 40 余篇,其中被 SCI 检索 16 篇、EI 检索 30 余篇. 翟海川,男,1988 年生,硕士研究 生,主要研究方向为多智能体系统. 第 14 届 IEEE 国际计算智能信息研讨会 14th IEEE International Symposium on Computational Intelligence and Informatics Authors are welcome to submit original and unpublished papers and attend the 14th IEEE International Symposium on Computational Intelligence and Informatics to be held on November 19—21, 2013 in Budapest, Hungary. The Symposium is organized with the focus of bringing together scientists from any country working on computational intel⁃ ligence and its applications with the aims at providing an opportunity for sharing and discussing the recent research devel⁃ opments in this field. The idea is to have a small number of lecturers and participants in a relaxed and informal atmos⁃ phere. Author’s Schedule Full paper submission: August 12, 2013 Notification: September 9, 2013 Final manuscript submission: October 7, 2013 Contact Secretary Anikó Szaká Óbuda University E⁃mail: szakal@ uni⁃obuda.hu Website: http: / / conf.uni⁃obuda.hu / cinti2013 / index.html 第 3 期 单素素,等:采用 Leader⁃follower 和模糊反馈机制的机器鱼队形控制 ·253·