智能系统：复杂网络上同时考虑感染延迟和非均匀传播的SIR模型

第8卷第2期 智能系统学报 Vol.8 No.2 2013年4月 CAAI Transactions on Intelligent Systems Apr.2013 D0I:10.3969/i.issn.16734785.201210027 网络出版t地址：htp://www.cnki.net/kcma/detail/23.1538.TP.20130419.1509.001.html 复杂网络上同时考虑感染延迟 和非均匀传播的SR模型 赵敬12，夏承遗12，孙世温2，王莉12 (1.天津理工大学天津市智能计算与软件新技术重，点实验室，天津300384；2.天津理工大学省部共建教育部计算 机视觉与系统重点实验室，天津300384) 摘要：为了能更有效地分析和理解传染性疾病的传播，提出了一个新颖的SR模型，在这个传播模型里同时考虑了 影响疾病传播行为的2个因素：感染延迟和非均匀传播.基于平均场理论和大量的数值仿真，给出了疾病传播临界 值的解析公式，并发现感染延迟和非均匀传播对临界值影响截然不同：感染延迟能够在很大程度上减小传播闽值， 促进疾病在人群中的传播；而非均匀传播能够增大传播临界值，阻碍疾病的大规模传播.当前的研究结果有助于深 人理解真实复杂系统中的疾病传播行为，充分考虑感染延迟、传播机制和实际人群的拓扑结构等因素在疾病传播中 的作用，从而为制定有效的传染病预防和控制措施提供理论依据， 关键词：感染延迟；非均匀传播；临界值；复杂网络；SR模型 中图分类号：TP18;0231.5文献标志码：A文章编号：16734785(2013)02012807 A novel SIR model with infection delay and nonuniform transmission in complex networks ZHAO Jing 2,XIA Chengyi2,SUN Shiwen2,WANG Li2 (1.Tianjin Key Laboratory of Intelligence Computing and Novel Software Technology;2.Key Laboratory of Computer Vision and Sys- tems (Ministry of Education),Tianjin University of Technology,Tianjin 300384,China) Abstract:In order to analyze and understand the spreading behavior of infectious diseases,the authors propose to examine susceptible-infected-removed (SIR)model.The researchers simultaneously introduce into the epidemic model the two factors:influencing disease spreading behavior,and infection delay and nonuniform transmission,u- tilizing the SIR model.Based on the mean-field approximation and large-scale numerical simulations,the analytical results of critical thresholds of disease spreading were derived,along with the infection delay and the nonuniform transmission having a distinct impact on the critical threshold.The infection delay can greatly decrease the critical threshold and facilitate the spread of epidemics,while the nonuniform transmission can augment the critical thresh- old and hinder the epidemic spreading in complex networks.Current results are conducive to further understand the epidemic spreading inside the complex real systems,as well as to fully consider the roles of infection delay,trans- mission factors and topological structure of population in the spreading of diseases.The results also provide a num- ber of theoretical evidence to design more effective epidemic prevention and containment measures. Keywords:infection delay;nonuniform transmission;critical threshold;complex networks;SIR model 近年来涌现了许多新兴的传染性疾病，例如SARS和禽流感等，这些传染病都曾经在全球的范 围内爆发，而每一次疾病的大规模爆发都会严重威 收稿日期：2012-10-16.网络出版日期：201304-19 基金项目：国家自然科学基金资助项目(60904063,61203138)；天津 胁人类的生命，造成经济财产的巨大损失，并在很长 市应用基础及前沿技术研究计划资助项目 一段时间里扰乱人们的正常生活13].因此，如何有 (11 JCYBJC06600);天津市高等学校科技发展基金资助项 目(20090813). 效地控制疾病传播等方面的课题已经引起了包括生 通信作者：夏承遗.E-mail:xialooking@163.com 物学、数学、统计物理、控制论和计算机科学等领域

第2期 赵敬，等：复杂网络上同时考虑感染延迟和非均匀传播的SR模型 ·129· 在内的诸多专家学者的关注[4].Kephart和 为NTD-SR模型)对传播阈值的影响，大量的仿真 White89]提出了基于传染病建模的均匀网络分析模 实验也证实了平均场解析的结果，表明了感染延迟 型，这个模型基于SIS(susceptible-infected-suscepti- 会减小传播阈值，增强疾病的传播；而非均匀传输增 ble)模型，并假设网络中的每个个体和其他任意一 大临界值，进而阻碍疾病的传播，这一结论有助于设 个个体接触的概率是相等的.Kermack和McKen- 计有效的疾病传播控制策略. drick研究了SR模型，他们的研究显示：在人口 1 NTD-SIR模型 密度低于某个特定值的时候，任何的疾病都不会在 网络上肆意地传播.非零传播阈值的发现是传染病 标准的SR模型将个体分为易感染者(S)、感 学研究史上的一个里程碑.然而，大量的证据显示现 染者(I)和康复者(R).易感染者是健康个体，但是 实世界中许多网络并不具备这种同质性，现实世界 以概率B∈[0,1]感染上疾病，感染者是已经感染疾 中网络往往兼具规则性和随机性，比如很多自然、社 病的患者并以概率γy∈[0,1]恢复成为康复者. 会和工程网络系统都被发现同时具有小世界特性 标准的SR模型可以用式(1)表示： (small--world,SW)和无标度(scale-free,SF)特 ds(t) 性2].人们把具有SW和SF等特性的真实网络 dt =-Bs(t)p(t), 称为复杂网络，复杂网络的研究为深入剖析现实世 dp(t) dt =Bs(t)p(t)-yp(t), (1) 界中网络拓扑结构对疾病或病毒的传播行为提供了 新的视角13].其中，Pastor-Satorras和Vespignani发 dr(t) dt =-yp(t). 表了一系列有影响的文章416，他们发现，在度分 布呈现幂律分布P(k)=k(P(k)表示一个节点度 式中：s(t)p(t)、(t)分别代表了健康个体、感染个 为k的概率)的网络（即无标度scale-free网络）中， 体和康复个体占总人数的百分比，且s()+p(t)+ 疾病传播临界值为入。=/.尽管这个假 (t)=1,有效传播率入=B/y,为不失一般性，取 设并不完全符合现实世界的情况，但是他们的研究 y=1. 隐含了一个重要的结论：若网络规模无限增大，当趋 本文所提出的NTD-SIR模型如图1表示，假设 于无限大时，无标度网络将不再有非零的传播阈值。 一个易感染个体(S),在t时刻被它的邻居感染，它 在文献[17]中，Moreno等使用SIR模型在SF网络 会保持已感染状态直到时间t+T+1(称T为感染 上做的实验也得到了相似的结论：在疾病传播期间， 延迟)，实际上，T是因人而异的，但是在这里假设T 当传播率大于某一个临界值的时候，疾病会大规模 对每个人都是相等的.，1，…，1表示不同时间阶 传播；否则，疾病会自发地消亡.因此，要想能够有效 段的状态为I的个体，在每个时间步，状态为S的个 地控制疾病在网络上的扩散，有必要找出传播阈值， 体将以概率入()被依次转换成为状态I。,然后依次 进而制定有效的抑制措施1825]」 进入I1,L2,…,Ir,只有状态为I,的个体能够以概率 经典的SIS和SIR模型假定感染个体不会被延 y被治愈成为状态为R的个体.在t时刻，一个已经 时治疗，并假定每个感染者试图感染其每一接触邻 感染的个体想要去感染它的所有状态为S的邻居， 居等，这些情况在现实条件下通常并不能满足.例 假设有效传播率入=B/Y是一个和度相关的函数 如，Wag等2基于SR模型考虑非均匀传输在疾 入(k),也就是说一个状态为I的个体的感染率不是 病传播中的作用，分析得到了相应的感染临界值公 简单地等于它的度. 式；Xu等研究了传播延时对SW和SF网络中疾 ⑧☑☑☑R 病传播的影响，实验结果证实了时间延迟能够极大 图1 NTD-SIR模型 地助长疾病的传播.在此基础上，文献[28]将时间 Fig.1 NTD-SIR epidemic model 延迟的概念引入到了S$模型中，并在局域世界网 1.1同质网络 络中做了仿真实验，结论证明了局域世界的大小和 在同质网络中，节点的度变化不大，度分布呈 感染延迟都能够促进疾病的传播.但是，文献[27- Poisson分布（如随机网络、小世界网络）或delta分 28]没有给出感染延时对感染临界值的影响，本文 布（如规则晶格），模型传播有如下特征， 同时将感染延迟和依赖于度的感染率的非均匀传输 定理1对于同质网络，NTD-SR模型的传播 引入到经典SR模型中，基于平均场理论研究改进 后的考虑非均匀传输和感染延迟的SR模型（简称 阔值为6(T+)当入<6时，疾病消亡

·130 智能系统学报 第8卷 系统稳定在无病平衡点；当入>A:时，系统稳定于 s(t)=e-Ao(k)"(T+)) 地方病状态平衡点. 又因为当t→∞时，p(∞)0，所以 证明在同质网络中每个节点的度近似等于它 s(o)=1-p(∞)-r(∞)=1-r(o)= 的平均度〈〉，利用平均场理论，系统演化可以用式 en倒(r1)以m) (2)表示： 可以推出： ds(t) =-A(k)(k)s(t)p(), r(0）=1-e4(+0〉=fr(0). dt 式中：函数f代r(∞)是关于r(∞)的严格递增函数， dpo(t) dt =-入(k)(k〉s(t)p(t)-po(t), (∞)=0是一个平凡解，代表疾病自发消亡，要使 疾病大规模传播则有 dpi(t) dt =-p1(t)+po(t), (2) dfr(∞)) >1. (5) dr()x)=0 1 dpr(t) dt =-pr(t)+pr-(t), 整理武(5)后得到5=(T+)从而，定 理1得证，并在特定条件（如不考虑感染延时）下， =pr(t). 可以得到下列结论： 推论1若不考虑时间延迟，即当T=0时，可 式中：入(k)代表一个健康个体通过一条边被感染的 概率，po(t),P1(t),…,Pr(t)表示状态分别为1，L1, 以得到A5=内转别地，当a=1时，A=卤与标 “,,的个体所占百分比.假设一个患病个体的感染 准的SIR模型结果一致[7 率与(k〉(0≤≤1)成比例，因此有入(k)= 推论2在α=0时，即个体被感染的概率与网 ,其中，是独立的感染因子.方程(2)可以 (居)a 络拓扑结构无关，不妨假设每个个体被感染的概率 改写成： 是常值，设为定值A,则临界阂值6=(T+1)A (as(t) =-(k〉s(t)p(t), 1.2异质网络 at 真实复杂系统（如社会网络和因特网）中，节点 po(t) dt =入(k)s(t)p(t)-P(t), 的度差异很大，度分布表现出强烈的重尾分布.在高 度异构无标度网络中，NTD-SIR传播模型的临界特 api(t) 性如定理2所述. ot =-p1(t)+po(t), (3) 定理2在异质不相关网络中，NTD-SR模型 apr(t) 上疾病爆发必须清足如下条件：古名A(), at =-pr(t)+pr-i(t), P(k)(T+1)>1,此时系统存在地方病状态平衡 ar(t) =p(t). 点，否则系统趋于无病平衡点，即疾病是否爆发由网 络的拓扑结构(P(k))、非均匀感染机制（入(k)以 在系统达到平衡点时，根据方程组(3)可以得 及感染延时共同决定， 到p,(_p,() 证明在异质网络中，系统的动态方程可以描述为 dt =0和p(t)= (as(t) P1(t)=…=pr(t).为了方便计算，不妨设p(t)= =-ks(t)⊙(t), ∑p(T),可以得到p()=p1(t)=…=pr= apk.o(t) =s(t)⊙(t)-Pk,o(t), = Ot 24在任意时刻：清足归一化条件()+p()+ aps.(t) dt =-p,(t)+p,o(t), (6) r(t)=1,根据方程组(3)得到： s(=-(k)s()p(0= ops.r(t) ar(t) Pr(t) at =-Pk,r（t)+pk,r-1(t), -A(k)(T+1)s(t). (4) ork(t) 将式(4)两边积分，得到 =pu.r(t)

第2期 赵敬，等：复杂网络上同时考虑感染延迟和非均匀传播的SR模型 ·131· 式中：P,o(t)Pk1(t),…,P,r(t)表示度为k且状态 1-3(o）=1-e(w10k） (11) 分别为1，，…，I的已感染个体所占的百分比， 当t→∞时，将式(11)带人式(10)可得 ⊙(t)表示一个健康的个体通过一条与其他个体相 连的边被感染的概率，因此⊙(t)可以表示为 (o)=高Ea(P(() .()=((() 高名M()P()I1-(0)】 式中：入(k)是每条边的平均感染率，P(t)是度数为 '的个体的相对密度，条件概率P(k'Ik)表示度数 有a()P[1-er] 为k的节点与度数为'的节点连接的概率。 g(Φ（∞）). 在度不相关的无标度网络里， 显然，g((∞))是关于中()的一个非负递 8.()=a(e)=A()P（pr( 增函数，很显然（∞）=0是它的一个平凡解，对应 ∑sP(s) 于无病平衡点；要使上述方程有一个非平凡解(01. 由方程组(6)的第1个方程左右两边积分可以得到 d[p(o)] () ()e 解上述方程，易得 d[g(Φ（∞）)] e2 P=e高A d[Φ(e)]pe)=0 (7) 否子KA()PE)[(T+1kea】 =0 在平衡态的时候有°P0=0,?=0,1, ∂t 杏2A(PE[T+1e灯- p(t)=∑P,r(T)表示度为k且状态为I的个体 T=0 高(A)P(T+D>1.(2) 的密度.平衡点的时候将p(t),Pk,o(t),…P,r（t), 定理2得证，并有如下推论： ⊙记为PPk,0,…,Pk,r,⊙因此在平衡点时，由式 推论3假定个体的感染率正比于它的度时， (6)得： 即a=1时，A(k)=Ak/k=入，代入式(12)，在网 ks(t)0(t)-Pk,o(t)=0, 络规模趋于无穷时，可以得到感染临界阈值为入6= -P,i(t)+p,o(t)=0, (8) 得十特别地，不考虑感染延时(T:0),结 -Pe,r（T)+p,r-1(t)=0. 果恢复为经典模型上的结论：G一器：另外。 由式(6)得到P,o(t)=p,1(t)=…=P,r(t)= 对于有限尺度的BA无标度网络，它的度分布满足 Pi(t) T+1 P(k)=20,平均度〈)=2m,最大度m= 由式(6)的最后1个方程两边积分可得 P(r)dr=(),因此式(7)可以改写为 m,(=广·2管k=hN.因此其临界 s(t)=eò2arrr*r0= 阈值表示为 1,〈k) 1 2 eBanrtro (9) 6=T+1‘)=T+1mnN 令 推论4假定个体的感染率完全独立于它的度 ()=否(P()(.(I0) 时，即α=0时，若一个个体的感染力为常值A,此时 将式(10)代入式(9)后得到s(t)=e(T+0.当 A()=,得到5=7中·六容易看出，此时疾 系统达到稳态时（即t→0时)，pk,o（∞）= 病传播阈值与网络拓扑结构无关特别地当T=0 pk,1()=…=pk,r（∞)=0，因此 时，A6= r(∞）=1-∑Px(∞)-s(∞）= 推论5一个个体的感染率与度成次线性关系

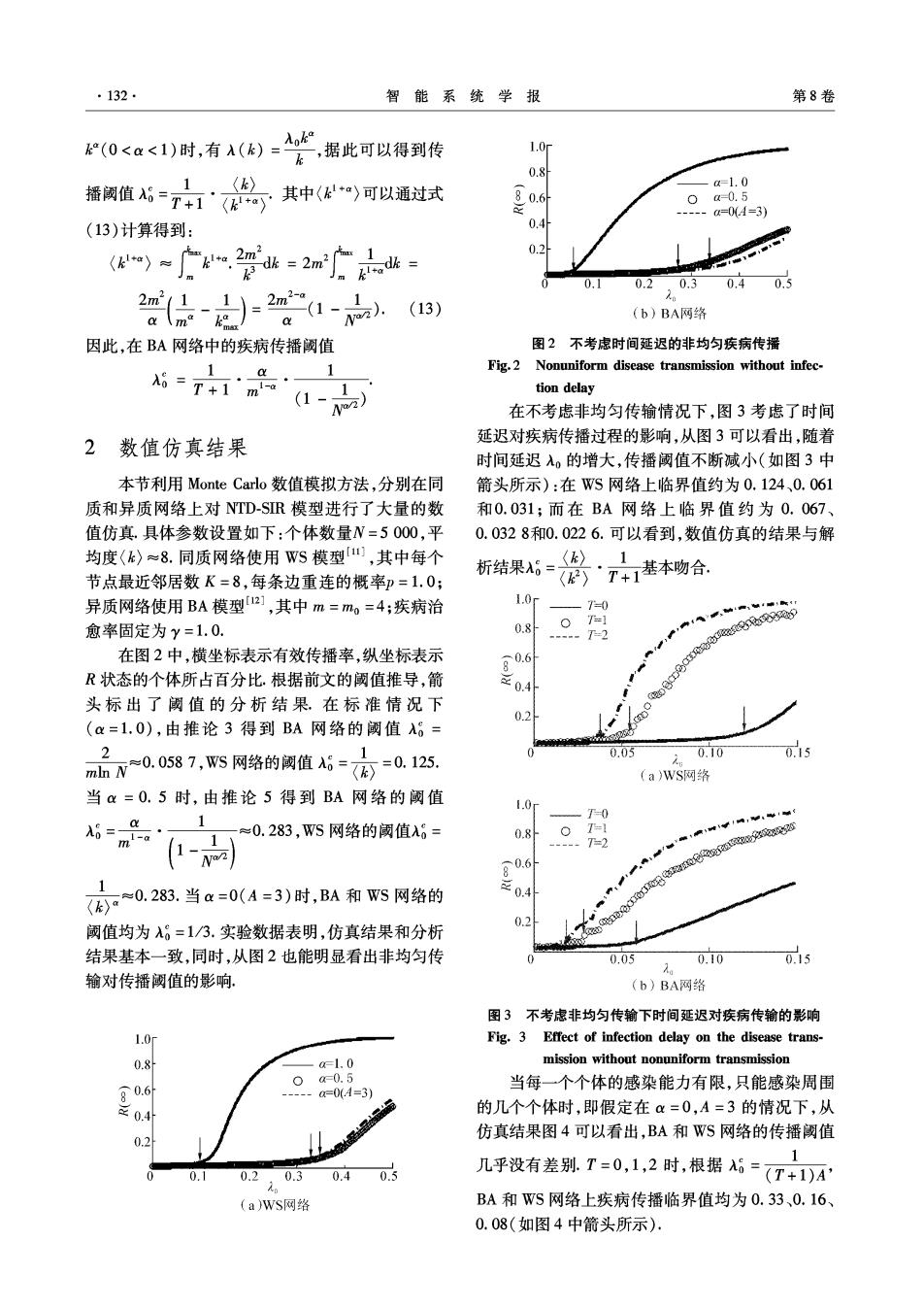
·132. 智能系统学报 第8卷 “(0<a<1)时，有A()然，据此可以得到传 1.0r 0.8 摇树值5=总其中似)可以通过试 a=1.0 80.6 0a-0.5 ---a=0A=3) (13)计算得到： 0.4 0.2 0 0.10.20.30.40.5 动2 1-a. (13) (b)BA网络 因此，在BA网络中的疾病传播阈值 图2不考虑时间延迟的非均匀疾病传播 Fig.2 Nonuniform disease transmission without infec- 6=T+1‘m。 1 tion delay 在不考虑非均匀传输情况下，图3考虑了时间 2数值仿真结果 延迟对疾病传播过程的影响，从图3可以看出，随着 时间延迟入。的增大，传播阈值不断减小（如图3中 本节利用Monte Carlo数值模拟方法，分别在同 箭头所示)：在WS网络上临界值约为0.124、0.061 质和异质网络上对NTD-SR模型进行了大量的数 和0.031；而在BA网络上临界值约为0.067、 值仿真.具体参数设置如下：个体数量N=5000,平 0.0328和0.0226.可以看到，数值仿真的结果与解 均度(k)≈8.同质网络使用WS模型，其中每个 析结果5= ()‘T+1基本吻合. 1 节点最近邻居数K=8,每条边重连的概率p=1.0; 异质网络使用BA模型2]，其中m=m=4;疾病治 1.0r T=0 愈率固定为y=1.0. 0.8 --。T-2 在图2中，横坐标表示有效传播率，纵坐标表示 80.6 R状态的个体所占百分比.根据前文的阈值推导，箭 0 头标出了阈值的分析结果.在标准情况下 0.2 (a=1.0),由推论3得到BA网络的阈值入6= 2 n品-0.0587，WS网络的阀值A5=高=0125， 0.05 。0.10 0.15 (a)WS网络 当a=0.5时，由推论5得到BA网络的阈值 1.0 T=0 A6 ml-a ≈0.283，WS网络的阈值入6= 0.8 ---.T=2 g0.6 a0.283.当Q=0(A=3)时，BA和WS网络的 三04 线2o流电Qe实宽6a文宽 阈值均为：=1/3.实验数据表明，仿真结果和分析 结果基本一致，同时，从图2也能明显看出非均匀传 0.05 .0.10 05 输对传播阈值的影响. (b)BA网路 图3不考虑非均匀传输下时间延迟对疾病传输的影响 1.0r Fig.3 Effect of infection delay on the disease trans- 0.81 -a1.0 mission without nonuniform transmission 0-0.5 a=0(A=3) 当每一个个体的感染能力有限，只能感染周围 0.4 的几个个体时，即假定在α=0，A=3的情况下，从 仿真结果图4可以看出，BA和WS网络的传播阚值 0.2 0.1 0.2 0.3 0.40.5 几乎没有差别T=0,1,2时，根据5=(T+)A (aWS网络 BA和WS网络上疾病传播临界值均为0.33、0.16、 0.08(如图4中箭头所示)

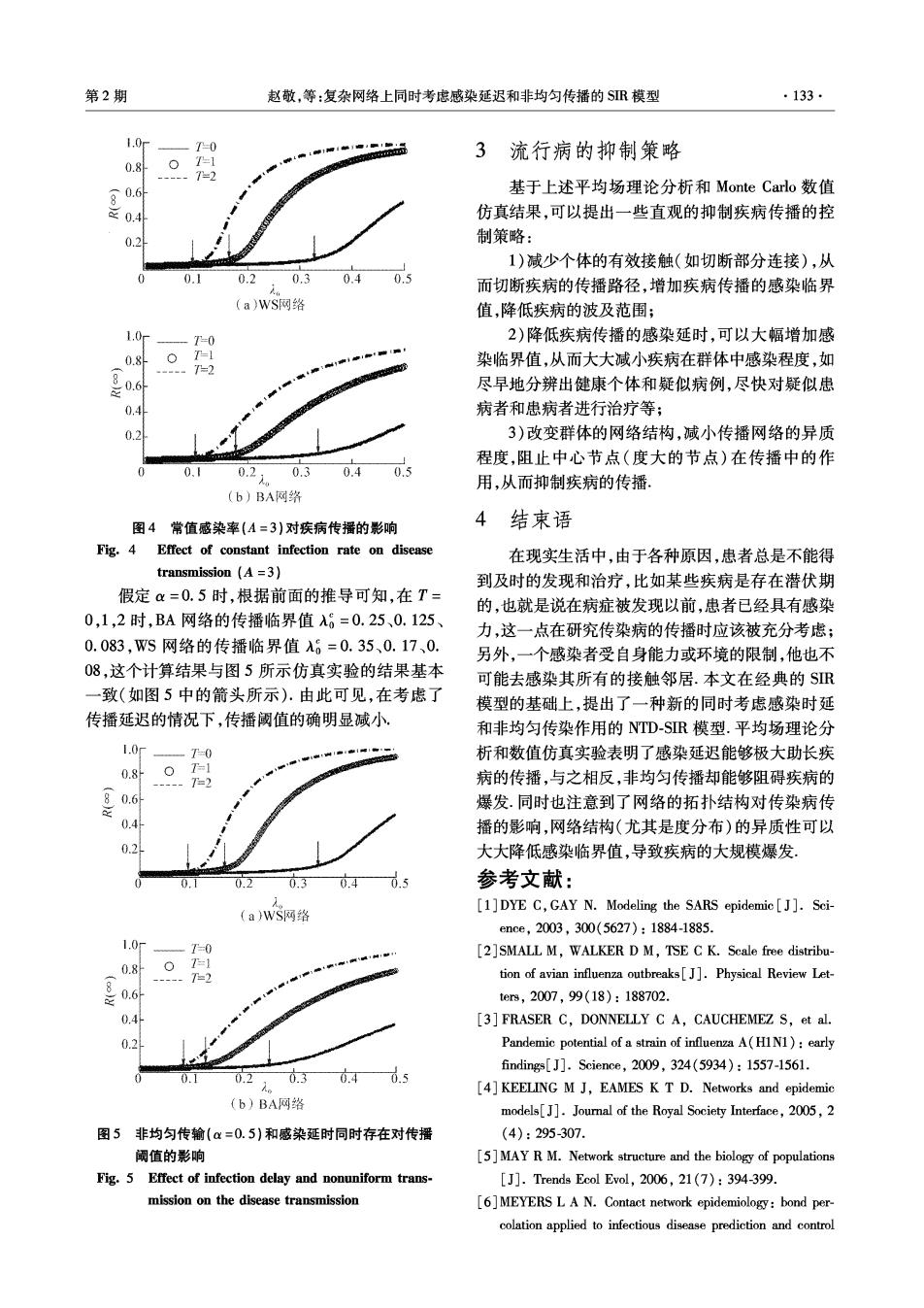
第2期 赵敬，等：复杂网络上同时考虑感染延迟和非均匀传播的SR模型 ·133· 1.0p -=0 3 01 流行病的抑制策略 0.8 -7=2 806 基于上述平均场理论分析和Monte Carlo数值 0.4 仿真结果，可以提出一些直观的抑制疾病传播的控 0.2 制策略： 1)减少个体的有效接触（如切断部分连接），从 0 0.1 0.2 0.3 0.4 0.5 而切断疾病的传播路径，增加疾病传播的感染临界 (a)WS网络 值，降低疾病的波及范围； 1.0 T-0 2)降低疾病传播的感染延时，可以大幅增加感 0.8 T=1 染临界值，从而大大减小疾病在群体中感染程度，如 --7-2 0.6 尽早地分辨出健康个体和疑似病例，尽快对疑似患 0.4 病者和患病者进行治疗等； 0.2 3)改变群体的网络结构，减小传播网络的异质 程度，阻止中心节点（度大的节点）在传播中的作 0. 0.2 0.3 0.4 0.5 用，从而抑制疾病的传播 (b)BA网络 图4常值感染率(A=3)对疾病传播的影响 4结束语 Fig.4 Effect of constant infection rate on disease 在现实生活中，由于各种原因，患者总是不能得 transmission（A=3)】 到及时的发现和治疗，比如某些疾病是存在潜伏期 假定α=0.5时，根据前面的推导可知，在T= 的，也就是说在病症被发现以前，患者已经具有感染 0,1,2时，BA网络的传播临界值A8=0.25、0.125、 力，这一点在研究传染病的传播时应该被充分考虑； 0.083,WS网络的传播临界值入6=0.35、0.17、0. 另外，一个感染者受自身能力或环境的限制，他也不 08,这个计算结果与图5所示仿真实验的结果基本 可能去感染其所有的接触邻居.本文在经典的SR 一致（如图5中的箭头所示）.由此可见，在考虑了 模型的基础上，提出了一种新的同时考虑感染时延 传播延迟的情况下，传播阈值的确明显减小. 和非均匀传染作用的NTD-SR模型.平均场理论分 1.0 T-0 析和数值仿真实验表明了感染延迟能够极大助长疾 0.8 T=1 病的传播，与之相反，非均匀传播却能够阻碍疾病的 0.6 爆发.同时也注意到了网络的拓扑结构对传染病传 0.4 播的影响，网络结构（尤其是度分布）的异质性可以 0.2 大大降低感染临界值，导致疾病的大规模爆发， 0.2 0.3 0.4 0.5 参考文献： [1]DYE C,GAY N.Modeling the SARS epidemic J].Sci- (a)WS网路 ence,2003,300(5627):1884-1885. 1.0 T=0 [2]SMALL M,WALKER D M,TSE C K.Scale free distribu- 0.8 -1 --T2 tion of avian influenza outbreaks[J].Physical Review Let- 0.6 tes,2007,99(18):188702. 0.4 [3]FRASER C,DONNELLY C A,CAUCHEMEZ S,et al. 0.2 Pandemic potential of a strain of influenza A(HIN1):early finding[J].Science,2009,324(5934):1557-1561. 0.1 0.2 0.40.5 [4]KEELING M J,EAMES K T D.Networks and epidemic (b)BA网路 models[J].Journal of the Royal Society Interface,2005,2 图5非均匀传输（α=0.5）和感染延时同时存在对传播 (4):295-307. 阈值的影响 [5]MAY R M.Network structure and the biology of populations Fig.5 Effect of infection delay and nonuniform trans- [J].Trends Ecol Evol,2006,21(7):394-399. mission on the disease transmission [6]MEYERS L A N.Contact network epidemiology:bond per- colation applied to infectious disease prediction and control

·134· 智能系统学报 第8卷 [J].Amercian Mathematical Society,2007,44(1):63- [21]LIU Zonghua,TANG Ming,LI Baowen.Epidemic sprea- 86. ding by objective traveling [J].Euro-Physics Letters, [7]夏承遗，刘忠信，陈增强，等.复杂网络上的传播动力学 2009,87(1):18005. 及其新进展[J].智能系统学报，2009,4(5)：392-397. [22]MELONI S,PERRA N,ARENAS A,et al.Modeling hu- XIA Chengyi,LIU Zhongxin,CHEN Zengqiang,et al. man mobility response to the large-scale spreading of infec- Transmission dynamics in complex networks [J].CAAI tious diseases[J].Scientific Reports,2011,1:62 Transactions on Intelligent Systems,2009,4(5):392-397. [23]GUO Weiping,LI Xiang,WANG Xiaofan.Epidemics and [8]KEPHART J O,WHITE S R.Directed-graph epidemiologi- immunization on education distance preferred small-world cal models of computer viruses [C]//Proceedings of the networks[J].Physica A,2007,380:684-690. IEEE Computer Society Symposium on Research in Security [24 ]SHI Hongjing,DUAN Zhisheng,CHEN Guanrong.An SIS and Privacy..[S.1.],UsA,1991:343-359. model with infective medium on complex networks J]. [9 KEPHART J O,WHITE S R.Measuring and modeling Phy9icaA,2008,387(8/9):2133-2144. computer virus prevalence[C]//Proceedings of the IEEE [25]GOMEZ S,ARENAS A,BORGE-HOLTHOEFER J,et Computer Society Symposium on Research in Security and al.Discrete-time Markovian chain approach to contact- Privacy.New York,USA,1993:2-15. based disease spreading in complex networks[J].Euro- [10]KERMACK W,MCKENDRICK A.A contribution to the physics Letters,2010,89(3):38009. mathematical theory of epidemics[J].Proceedings of the [26]WANG Jiazeng,LIU Zengrong,XU Jianhua.Epidemic Royal Society of Medicine,1927,115(772):700-721. spreading on uncorrelated heterogeneous networks with [11]WATTS D J,STRONGATZ S H.Collective dynamics of non-uniform transmission[J].Physica A,2007,382(3): small-world networks[J].Nature,1998,393:440-442. 715-721. [12]BARABASI A L,ALBERT R.Emergence of scaling ran- [27]XU Xinjian,PENG Haiou,WANG Xiaomei,et al.Epi- dom networks[J].Science,1999,286(5439):509-512. demic spreading with time delay in complex networks[J]. [13]BOCCALETTI S,LATORA V,MORENO Y,et al.Com- Physica A,2006,367:525530. plex networks structure and dynamics[J].Physics Re- [28 XIA Chengyi,LIU Zhongxin,CHEN Zengqiang,et al. p0rts,2006,424(4/5):175-308. Epidemic spreading behavior with time delay on local- [14 PASTOR-SATORRAS R,VESPIGNANI A.Epidemic world evolving networks[J].Front Electr Electron Eng spreading in scale-free networks J].Physical Review China,2008,3(2):129-135. Letters8,2001,86(14):3200-3203. 作者简介： [15]PASTOR-SATORRAS R,VESPIGNANI A.Epidemic dy- 赵敬，女，1986年生，硕士研究生， namics and endemic states in complex networks[J].Phys- 主要研究方向为复杂网络上病毒传播。 ical Review E,2001,63(6):066117. [16]PASTOR-SATORRAS R,VESPIGNANI A.Immunization of complex networks J].Physical Review E,2002,65 (3):036104. [17]MORENO Y,PASTOR-SATORRAS R,VESPIGNANI A. Epidemic outbreaks in complex heterogeneous networks 夏承遗，男，1976年生，副教授，博 [J].European Physical Joumal B-Condensed Matter and 士，主要研究方向为复杂系统与复杂网 Complex Systems,2002,4(26):521-529. 络建模分析、传播动力学、演化博奔动 [18]NEWMAN M E J.The spread of epidemic disease on net- 力学等.获天津市科技进步三等奖1 work [J].Physical Review E,2002,66:016128. 项，目前主持国家自然科学基金1项， [19]BOGUNA M,PASTOR-SATORRAS R,VESPIGNANI A. 省部级科研项目1项，其他科技计划1 Absence of epidemic threshold in scale-free networks with 项.发表学术论文30余篇，其中被SCI检索近20篇， degree correlations[J].Physical Review Letters,2003, 90(2):028701. 孙世温，女，1980年生，讲师，博士， [20]许丹，李翔，汪小帆.局域世界复杂网络中的病毒传播 主要研究方向为复杂动态网络、网络鲁 及其免疫控制[J].控制与决策，2006,21(7)：817- 棒性、软件工程.主持完成天津市高等学 820. 校科技发展基金1项、目前在研国家自 XU Dan,LI Xiang,WANG Xiaofan.On virus spreading 然科学基金1项.发表学术论文近10 in local-world complex networks and its immunization con- 篇，其中被SCI检索3篇，检索4篇. trol[J].Control and Decision,2006,21(7):817-820