
第7卷第6期 智能系统学报 Vol.7 No.6 2012年12月 CAAI Transactions on Intelligent Systems Dec.2012 D0I:10.3969/i.issn.16734785.201205011 网络出版t地址:htp://www.cnki.net/kcma/detail/23.1538.TP.20121116.1700.002.html 交互学习的粒子群优化算法 秦全德,李丽,程适23,李荣钩 (1.深圳大学管理学院,广东深圳518060;2.英利利物浦大学电气电子工程系,英国利物浦L693G;3.西交利 物浦大学电气电子工程系,江苏苏州215123:4.华南理工大学工商管理学院,广东广州510640) 摘要:分析基本的粒子群优化学习机制的缺陷,启发于人类社会不同群体之间可以交互学习的特点,提出了一种 改进粒子群优化算法一LPS0.在LPS0算法中,粒子由2个种群构成.当2个种群中最佳的全局最优位置在连续 一定的迭代次数内没有改善时,执行交互学习策略.依据每个种群的全局最优位置的适应值,运用模拟退火的机制 和轮盘赌的方法确定学习种群和被学习种群.提出了一个基于适应度排序的经验公式,计算学习种群中的每个粒子 向被学习种群学习的概率.为了摆脱选择压力,采用了一种速度变异的方法.多个测试函数的数值实验结果表明,L PS0具有较好的全局搜索能力,是一种求解复杂问题的有效方法. 关键词:粒子群优化算法;交互学习;学习策略;学习行为:群体多样性 中图分类号:TP18文献标志码:A文章编号:16734785(2012)06054707 Interactive learning particle swarm optimization algorithm QIN Quande',LI Li',CHENG Shi23,LI Rongjun (1.College of Management,Shenzhen University,Shenzhen 518060,China;2.Department of Electrical Engineering and Electron- ics,Liverpool University,Liverpool L69 3GJ,UK;3.Department of Electrical and Electronics Engineering,Xian Jiaotong-Liverpool University,Suzhou 215123,China;4.School of Business Administration,South China University of Technology,Guangzhou 510640, China) Abstract:Analyzing the drawbacks of learning mechanism in the basic particle swarm optimization(PSO),an in- teractive learning particle swarm optimization (ILPSO)is presented,which is inspired by the phenomenon in hu- man society that individuals in different groups can learn each other.Particles are composed of two populations in ILPSO.When the best particles fitness value of two populations does not improve within a certain number of suc- cessive iterations,interactive learning strategies are implemented.According to the best particle's fitness value of each population,a simulated annealing mechanism and roulette method are used to identify the learning population and the learned population.This paper proposes an empirical formula of sorting fitness value to calculate the proba- bility of each particle in the learning population learning from the learned population.In order to escape selection pressure,a speed mutation method is used.The numerical experimental results of some benchmark functions show that ILPSO has good global search capability and is an effective method for solving complicated problems. Keywords:particle swarm optimization algorithm;interactive learning;learning strategy;learning behavior;popu- lation diversity 粒子群优化(particle swarm optimization,PSO) 了鸟群觅食过程中的迁徙和群集行为.PS0算法 算法是一种基于种群搜索的随机优化技术,其模拟 具有概念简单、控制参数少、收敛速度快和易于编程 收稿日期:20120507.网络出版日期:2012-11-16 实现的优点21,自提出以来受到广大学者的关注 基金项目:国家自然科学基金资助项目(71071057,71001072);广东 但PS0算法同其他的随机搜索方法类似,在求解复 省自然科学基金资助项目(S2011010001337). 通信作者:秦全德.E-mail:qinquande@mail.com. 杂多峰函数时,容易陷入局部最优3].为了提高算

548 智能系统学报 第7卷 法性能,较多学者提出了基于不同思想的改进算法, 解.在D维的搜索空间中,粒子i在t次迭代时的状 可以简单归纳为以下几类:1)调节算法的参数451; 态属性由位置向量X=[x花2…n]和速度 2)群体拓扑结构的改进6]:3)与其他优化算法混 向量V=[,…o]进行描述.。e(l4, 合[891;4)嵌入生物行为机制01:5)设计新的学习 策略23 ua),∈(vin,vmm),其中la和uu分别为搜索空间 的下限和上限,d=1,2,…,D,a和vms是由用户设 在基本PS0算法中,粒子通过向个体最优位置 定的粒子飞行的最小和最大速度.粒子的好坏由一 和群体最优位置学习并不断调整其飞行速度和所在 个事先设定的适应度函数来确定.在算法的迭代过 位置,从而实现在搜索空间寻优.这样的学习策略使 程中,每一个粒子通过向个体最优位置和群体最优 得群体内的信息交流速度快,但由于学习方向的单 位置进行学习,按照式(1)和式(2)更新飞行速度和 一性,容易产生“趋同”现象,在算法性能上表现为 位置,从而在搜索空间内寻优 迭代后期搜索缓慢甚至停滞,容易陷入局部最 优4.因此,设计新的粒子学习策略是提高PS0算 i=w+c1(p4-x)+cn2(p4-x), 法性能的一个重要途径.目前,国内外学者已经在这 (1) 方面开展了一些研究.Liang等提出了广泛学习的 =太短+. (2) PS0算法,其每个粒子根据学习概率来决定向自身 式中:P=[p,p2…pa]表示粒子i的个体最 个体最优位置还是其他的个体最优位置进行学 优位置;P=[pgP2…Pn]是整个粒子群体 习].实验结果表明,采用广泛学习策略能够探索 的最优位置;1、2为均匀分布在[0,1]的随机数; 更大的搜索空间,保持了群体多样性,算法在搜索过 ℃1、c2为正的加速系数;w称为惯性权重,用于控制 程中不容易陷入局部最优,适合于多峰函数的求解. 先前速度对于当前速度的影响,从而协调粒子搜索 根据多精英比单精英更能够引导群体学习的社会现 的开发(exploration)和开采(exploitation).Shi等经 象,Huang等提出了基于榜样学习的改进PS0算 过多组实验,提出ω按照如式(3)线性递减变化4: 法1.文献[15]引入了超球坐标的方式来更新粒子 w=(ω,-w)×(tnm-t)/tns)+。.(3) 速度,设计了一种集成学习PS0算法.Wang等提出 式中:t.和t分别表示最大迭代次数和当前的迭代 了一种自适应学习的PS0算法,该算法依据搜索的 次数,ω,和①。分别表示算法初始和停止时的惯性 进程进行调整学习概率,在具有不同优点的4种学 权重.文献[4]的研究结果表明当ω,=0.9,w。=0.4 习策略中进行自适应选择l6],Peram等提出了适应 时,算法具有较好的性能.将文献[4]这种惯性权重 度值-距离-比例的S0算法,此算法中每个粒子 按照式(3)递减的PS0算法称为标准粒子群优化算 的每一维根据适应度值一距离-比例原则确定一个 法(SPSO) 新的学习对象 人类社会中不同群体之间存在资源和特质的差 2交互学习的粒子群优化算法 异性,个体不但会吸收所在群体的经验,而且还会同 2.1交互学习策略 其他群体进行信息交流.因此,人类社会的学习行为 在ILPS0中,粒子分成Swam,和Swam22个 可以发生在个体与个体、个体与群体以及群体与群 种群.算法初始运行时,2个种群均按照式(1)更新 体之间,启发于人类社会的学习行为特点,本文提出 速度.Swam,中粒子i在t次迭代的位置向量、速度 了一种由2个种群组成的交互学习的粒子群优化算 向量、个体最优位置和群体最优位置分别记为X,! (interactive learning particle swarm optimization, LPS0).当2个种群中最佳的全局最优位置在连续 ,1、P和P,.将上述4个向量的下标“1”改成 一定的迭代次数内没有改善时,开始实施交互学习 “2”就代表Swam,相对应的向量.设P,l、Pg.z的适 策略.交互学习的策略使得粒子学习的方向具有了 应度表示为P和P2,P表示t次迭代时2个种 多样性,为算法摆脱局部最优提供了新的额外动力. 群中最佳的全局最优位置,其适应度表示为P。= 仿真实验结果表明,LPS0在搜索的过程中能够较 min(fP,1fPg,2).当P在连续的k次迭代中如果没 好地保持群体的多样性,具有较好的全局寻优能力, 有改善时,即P-P*=0,表明算法陷人了局部 是一种求解复杂问题的有效方法, 最优,2个种群开始实施交互学习策略,其主要步骤 如下: 1粒子群优化算法框架 1)确定学习种群和被学习种群.启动交互学习 PS0算法中的每个粒子视为问题的一个可行 策略时,其中一个种群将仍然维持原有的方式进行

第6期 秦全德,等:交互学习的粒子群优化算法 ·549· 寻优,称之为被学习种群;改变原有的学习方式的种 在任意一个种群中随机选择一个粒子在任一维上的 群称为学习种群.根据P!和P2的值,采用模拟 速度按式(8)发生变异: 退火的方法确定Swarm,和Swarm2作为被学习种群 0.5×0mm×T4, T3<0.5; 的概率.这样的方式使得群体最优位置相对较差的 ,=1-0.5x0m×4,其他 (8) 种群将以一定的概率作为被学习种群,从而增加了 式中:m表示粒子飞行的最大速度,I3和T4表示均 算法的全局搜索能力.用ps表示Swam1被选择作 匀分布在[0,1]的随机数.由于只选择一个种群中 为被学习种群的概率,依据模拟退火算法的原理易 的一个粒子一维的速度发生变异,因此几乎不会破 有式(4): 坏群体的结构.但每一个种群、每一个粒子和其每一 匹-严2 e 维速度从统计意义上来说是以同样的概率被选择发 (4) 了。r2 生变异. e = 2.3LPS0主要步骤 式中:T表示模拟退火的温度.依据s的大小,采用 LPS0的主要步骤如下: 轮盘赌的抽样方法确定学习种群和被学习种群.抽 1)置t=0;初始化2个种群粒子的位置和速 取在[0,1]均匀分布的随机数,小于ps时,Swam1 度,并设定相应的参数; 为被学习种群,反之Swam2将作为被学习种群. 2)计算粒子适应度值,确定个体最优位置和群 2)确定学习种群中每个粒子向被学习种群学 体最优位置: 习的概率.在LPS0中,根据学习种群中单个粒子 3)P-P*=0&t≥k是否满足,若满足执行 适应度值的排序来决定学习概率的大小.学习种群 则4),否则直接转到6); 中适应度好的粒子向被学习种群学习的概率相对较 4)确定学习种群和被学习种群; 小,以尽量维持目前良好的搜索形态;反之学习种群 5)计算学习种群中每个粒子向被学习种群学 中适应度值较差的粒子,学习概率较大.依据经验公 习的概率; 式(5)确定学习种群中粒子i向被学习种群的学习 6)更新2个种群的粒子速度和位置; 概率pc 7)执行变异算子; pe:=0.1+0.5 x (order )3 (5) 8)t=t+1:计算粒子适应度,更新每个粒子的 m 个体最优位置和群体最优位置; 式中:oder:表示按粒子i在学习种群内适应度的排 9)判断程序终止条件是否满足,若满足则算法 序;m表示学习种群的规模. 终止,输出最优解,否则转到3) 3)更新每个种群的速度和位置.被学习种群的 粒子按照式(1)更新速度;在学习种群中,如果产生 3仿真实验 的随机数小于pc,粒子i同时向个体最优位置、群 3.1测试函数 体最优位置和被学习种群的群体最优位置学习更新 本文选取了11个常用的测试函数进行仿真实 速度;反之仍然根据式(1)更新速度.当Swam1是 验.其中基本测试函数包括2个单峰函数和f方、 学习种群时,向Swarm.2学习的粒子速度按照式(6) f。4个多峰函数f和f)1分别是偏移测试函数 更新.而当Swam2是学习种群时,向Swam学习的 和旋转测试函数.基本测试函数的局部极值点多沿 粒子速度按照式(7)更新: 着平行的坐标轴,且全局最优位于原点,不能较好地 va=ov curu(pia)+ 反映现实中优化问题的复杂性.Suganthan等对基本 Cur (Pal-)+cr(P2-),(6) 测试函数进行了偏移和旋转].是将基本测试 =om2+c1r2(p,2-2)+ 函数和f的全局最优点随机移动到每一维具有 carm(pa2-a2)+csrs(pgal-2).(7) 不同数值的新位置,并且加上了一个偏置值0.本文 式中:T(i=1,2,j=1,2,3)表示在[0,1]内均匀分 依据文献[18]的方法进行偏移.旋转测试函数f~ 布的随机数 f是通过将一个正交矩阵左乘f方乃和∫而得到的, 2.2变异算子 其各个变量之间变得都不可分.其中正交矩阵的产 如果Swam,和Swam2的群体最优位置的适应 生采用Salomon在1996年提出的方法191.表1给出 度值相差较大时,式(4)会给算法带来较大的选择 了每个函数的名称、数学表达式、搜索范围和最优值。 压力,不利于全局搜索.基于这样的考虑,本文采用
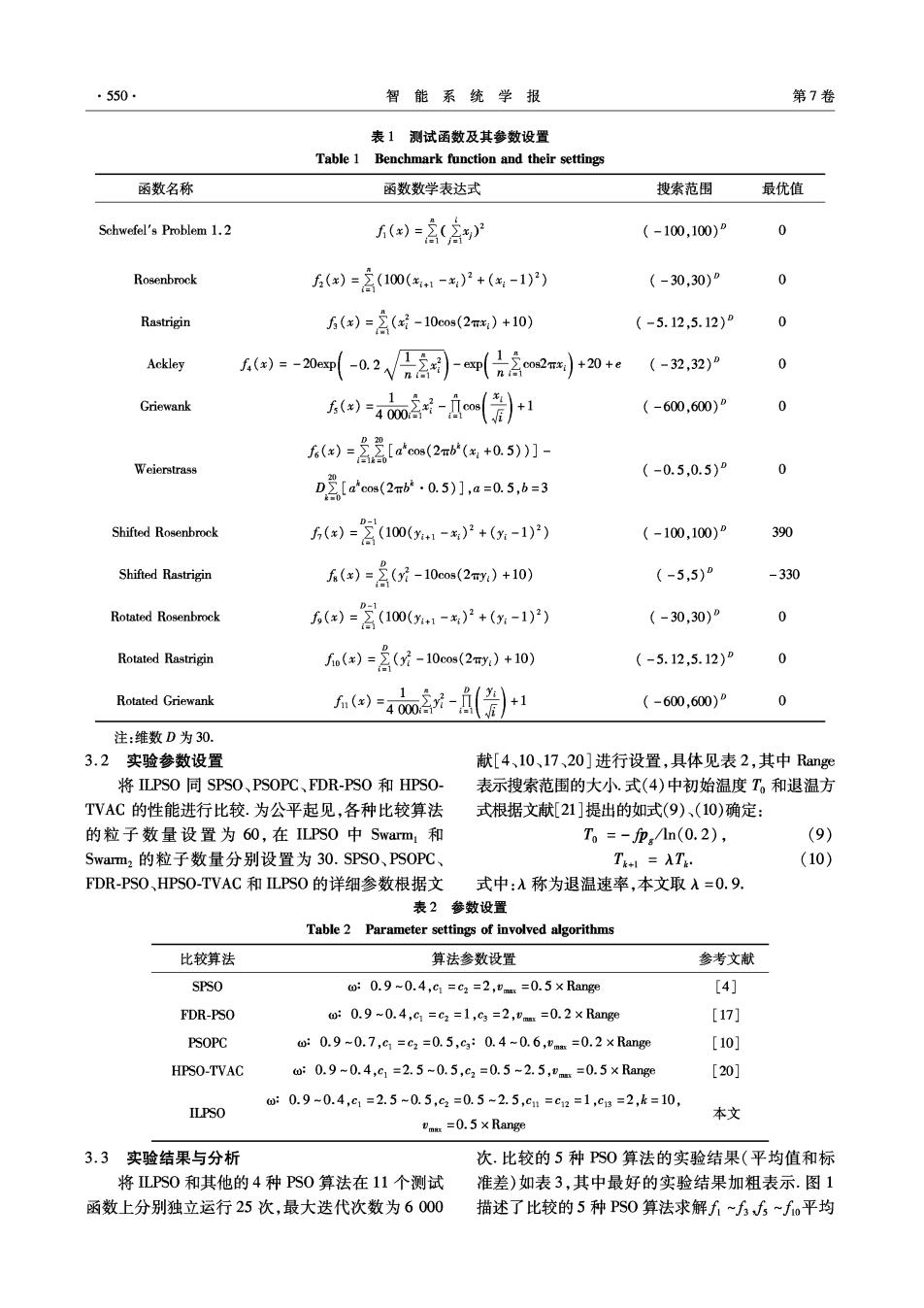
550. 智能系统学报 第7卷 表1测试函数及其参数设置 Table 1 Benchmark function and their settings 函数名称 函数数学表达式 搜索范围 最优值 Schwefel's Problem 1.2 ()=含(含 (-100,100)P 0 Rosenbrock 6()=含(100(1-)2+(属-1)) (-30,30)P Rastrigin 5()=含(-10eos(2m,)+10) (-5.12,5.12)D 0 Ackley i)=-20e(-02√日3-eh2m2m)+20+e (-32,32)D Griewank ()=40o8-ow()+1 (-600,600)° ())=含2[dcs(2ms(+05)]- Weierstrass (-0.5,0.5)P 0 D2[acos(2mb.0.5)],a=0.5,b=3 Shifted Rosenbrock 5(倒=含(10(31-)2+0-1)5 (-100,100)D 390 Shifted Rastrigin 无()=含(7-10cos(2m)+10) (-5,5)P -330 D-1 Rotated Rosenbrock 6()=含(100(1-)2+(-1)P) (-30,30)° 0 Rotated Rastrigin n()=2(-10cs(2m)+10) (-5.12,5.12)D 0 Rotated Griewank (-600,600)P 0 注:维数D为30. 3.2实验参数设置 献[4、10、17、20]进行设置,具体见表2,其中Range 将ILPSO同SPS0、PSOPC、FDR-PSO和HPSO- 表示搜索范围的大小.式(4)中初始温度T。和退温方 TVAC的性能进行比较.为公平起见,各种比较算法 式根据文献[21]提出的如式(9)、(10)确定: 的粒子数量设置为60,在ILPS0中Swarm1和 T。=-p小n(0.2), (9) Swam2的粒子数量分别设置为30.SPS0、PSOPC、 Tie ATy. (10) FDR-PS0、HPSO-TVAC和LPSO的详细参数根据文式中:入称为退温速率,本文取A=O.9. 表2参数设置 Table 2 Parameter settings of involved algorithms 比较算法 算法参数设置 参考文献 SPSO o:0.9-0.4,c1=c2=2,"m=0.5×Range [4] FDR-PSO w:0.9~0.4,c1=c2=1,c3=2,pm=0.2×Range [17] PSOPC w0.9~0.7,G1=c2=0.5,c:0.4-0.6,"nm=0.2×Rang0 [10] HPSO-TVAC w:0.9-0.4,c1=2.5-0.5,c2=0.5-2.5,mm=0.5×Range [20] w0.9-0.4,c1=2.5-0.5,c2=0.5~2.5,c1=c2=1,cg=2,k=10, ILPSO 本文 mr=0.5×Range 3.3实验结果与分析 次.比较的5种PS0算法的实验结果(平均值和标 将ILPS0和其他的4种PS0算法在11个测试 准差)如表3,其中最好的实验结果加粗表示.图1 函数上分别独立运行25次,最大迭代次数为6000 描述了比较的5种Ps0算法求解f~f方,5~fo平均

第6期 秦全德,等:交互学习的粒子群优化算法 ·551· 最优值的变化曲线, 表3各种算法的测试结果比较 Table 3 Comparisons of experimental results 比较的PS0算法 函数 指标 SPSO PSOPC FDR-PSO HPSO-TVAC ILPSO 平均值 5.88×10-14.37×10-21.03×10-81.79×10-72.50×10-0 标准差 4.45×10-18.37×10-22.28×10-82.23×10-72.37×10-0 平均值 3.07×10 2.01×101 2.19×104.22×10-17.64×10-1 标准差 2.61×101 1.78×103 2.95×101 8.29×10-16.57×10- 平均值 1.98×1012.00×101.83×10 6.92 1.99×10-1 6 标准差 5.35 9.11 6.04 4.23 2.19×101 平均值6.22×10-154.09×10-157.11×10-153.71×10-41.19×10-4 标准差5.41×10-151.84×10-52.51×10-51.27×10-43.01×10-5 平均值1.51×10-24.43×1031.41×1021.03×1027.11×104 标准差 2.21×10-25.92×10-31.66×10-21.02×10-22.33×10-3 平均值1.03×10-23.99×10-11.71×10-39.52×10-4 0 f后 标准差 9.83×10-35.42×10-12.73×10-38.19×10-14 0 平均值 5.01×102 4.15×102 4.02×1024.14×102 3.97×102 标准差 1.15×1022.73×101.11×102.71×10 6.41 平均值 -2.69×102-3.09×102-3.03×102-3.21×102-3.30×102 标准差 1.74×10 5.66 1.02×10 4.15 3.12×10-1 平均值 5.96×10 1.15×10 8.83 4.75×10 1.62 标准差 6.97×101 1.61 3.48 9.04×10 9.62×10-1 平均值 7.83×10 5.90×10 6.55×101 2.53×102 4.19×10 标准差 1.95×101 1.18×10 1.82×101 3.70×10 9.28 平均值1.62×10-21.23×10-22.15×10-21.38×10-24.42×10-3 标准差1.40×10-21.32×10-22.84×10-21.54×10-26.17×10-1 对于,ILPS0的求解结果都优于其他4种算 试函数f方和f,LPS0求解结果的平均值和标准差 法.在对“香蕉函数”方的优化中,相较于SPS0、 都明显好于其他算法.将函数的坐标轴进行旋转后, PSOPC和FDR-PS0,ILPS0和HPS0-TVAC在搜索 求解的难度将会提高.LPS0对旋转测试函数f)~ 过程中没有陷入局部最优.虽然LSO实验结果的 f:的实验结果仍表现出了好的搜索精度和鲁棒性, 平均值稍差于HPSO-TVAC,但标准差较小,表明 表明了其具有很好的适应性.综上分析,LPS0在对 ILPSO具有较好的鲁棒性.对于具有大量局部最优 基本测试函数、偏移测试函数和旋转测试函数的求 点的复杂多峰函数方和f6,LPS0体现了很好的优 解中都表现了搜索精度高和鲁棒性好的特点,特别 化效果,在搜索过程中一直没有陷入局部最优,说明 对复杂的函数,其优秀的搜索性能更加突出. 了交互学习策略能够摆脱局部最优的有效性.比较 在LPS0中,由于交互学习策略的作用,每个 的各算法在求解函数f的性能差别不大,都搜索到 粒子群体的多样性得到维护,从而提高了全局搜索 比较满意的结果.在求解f中,SPS0、PSO-FDR和 能力,不容易陷入局部最优.根据“没有免费午餐定 HPS0-TVAC的搜索精度只能达到10-2数量级, 理”,在维护粒子群体多样性的同时也带来了收敛 PSOPC的搜索精度为10-3数量级,而LPS0的搜索 速度相对不够快的成本.从图1中可以看出,ILPSO 精度达到了104数量级且标准差最小.对于偏移测 的收敛速度虽然快于SPS0和HPSO-TVAC,但在一

·552 智能系统学报 第7卷 些测试函数的优化上比PSOP℃和FDR-PSO的收敛 速度稍慢, 3.0r 7 2.5 2.0 1.5 1.0 0.5 0 0.5 34 迭代次数 迭代次数 迭代次数 (a)f (b)5 (c)f 60+ 5.6 5.2 4.8 -10 4.4 10 =4 23456 234 610 4.0 3.4610 迭代次数 达代次数 迭代次数 (d)f (e)f后 (f)f 2.5×10 3.0r -2.6 2.8 -2.7 2.6 2.4 -2.9 4 2.2 -3.0 -31 1.8 -3.2 1.6 -3. 0 10 0 1 3456 5 6 1 2 3456 逃代次数 迭代次数 达代次数 -SPSO--PSOP℃ PSO-FDR --HPSO-TVAC --ILPSO (g) (h)f. (j)fio 图1各种算法实验结果的平均最优值变化 Fig.1 The convergence curve of invdved algorithms 4 结束语 测试函数的实验结果表明LPS0具有较高的搜索 精度和鲁棒性,特别在求解复杂的问题中,体现的优 在分析基本PS0算法学习策略缺陷的基础上, 化性能更加突出.如何在保证LPS0搜索精度和鲁 启发于人类社会学习的特点,本文提出了一种交互 棒性的同时,并进一步提高收敛速度,以及将LPS0 学习的PS0算法—LPS0.交互学习策略中学习 应用到实际问题的求解中是未来研究的重点, 种群和被学习种群在搜索的过程中能够相互转换, 且改善了粒子学习方向“单一性”的缺陷,保证了群 参考文献: 体的多样性,从而提高了算法的全局搜索能力.多个 [1]EBERHART R C,KENNEDY J.Particle swarm optimiza-

第6期 秦全德,等:交互学习的粒子群优化算法 ·553· tion C]//IEEE International Conference on Neural Net- [12]LIANG J J,OIN K,SUGANTHAN P N.Comprehensive works.Perth,Australia,1995:1942-1948. leamning particle swarm optimization for global optimization [2]KENNEDY J,EBERHART R C.Empirical study of particle of multimodal functions[J].IEEE Transactions on Evolu- swarm optimization[C]//Proc of Congress on Evolutionary tionary Computation,2006,6(3):281-295. Computation.Washington,DC,USA,1999:1945-1949. [13]HUANG H,QIN H,HAO Z F,et al.Exampled-based [3]ANGELINE P J.Evolutionary optimization versus particle learning swarm optimization for continuous optimization swarm optimization and philosophy and performance differ- [J].Information Sciences,2011,182(1):125-138. ence[C]//Proc of 7th Annual Conference on Evolutionary [14]CLERC M,KENNEDY J.The particle swarm:explosion, Programming.San Diego,USA,1998:601-610. stability,and convergence in multi dimensional complex [4]SHI Y,EBERHART R C.A modified particle swarm opti- space[J].IEEE Transactions on Evolutionary Computa- mizer[C]//IEEE Congress on Evolutionary Computation tion,2002,6:58-73. Anchorage.AK,NJ,1998:69-73. [15]SABAT S L,UDGATA S K.Integrated leaming particle [5]FAN S K S,LIANG Y C.ZAHARA E.Hybrid simplex swarm optimizer for global optimization[].Applied Soft search and particle swarm optimization for the global optimi- Computing,2011,11(1):574-584. zation of multimodal functions[J].Engineering Optimiza- [16]WANG Y,LI B,WEISE T,et al.Self-adaptive leaming tion,2004,36:401418. based particle swarm optimization[J].Information Sci- 6]SUGANTHAN P N.Particle swarm optimizer with neighbor- ences,2011,182(20):4515-4538. hood operator[C]//Proc of the IEEE Congress of Evolution- [17]PERAM T,VEERAMACHANENI K,MOHAN C K.Fit- ary Computation.Washington DC,USA,1999:1958- ness-distance-ratio based particle swarm optimization 1961. C]//Proc of the Swarm Intelligence Symposium.Indian- [7]杨雪榕,染加红,陈凌,等.多邻域改进粒子群算法[J]. apolis,USA,2003:174-181. 系统工程与电子技术,2010,32(11):2453-2458. [18]SUGANTHAN P N,HANSEN N,LIANG J J,et al.Prob- YANG Xuerong,LIANG Jiahong,CHEN Ling,et al.Multi- lem definitions and evaluation criteria for the CEC 2005 neighbourhood improved particle swarm optimization algo- special session on real-parameter optimization[R/OL].ht- rithm[J].Systems Engineering and Electronics,2010,32 tp://www.ntu.edu.sg/home/EPNSugan. (11):24532558, [19]SALOMON R.Reevaluating genetic algorithm performance [8]杨帆,胡春平,颜学峰.基于蚁群系统的参数自适应粒子 under coordinate rotation of benchmark functions[J].Bio- 群算法及其应用[J].控制理论与应用,2010,27(11): 8y8tems,1996,39:263-278. 1479-1488. [20]RATNAWEERA A,HALGAMUGE S K,WATSON H C. YANG Fan,HU Chunping,YAN Xuefeng.Particle swarm Self-organizing hierarchical particle swarm optimizer with optimization algorithm of self-adaptive parameter based on time-varying acceleration coefficients[J].IEEE Transac- ant system and its application[J].Control Theory Appli- tions on Evolutionary Computation,2004,8 (3):240- cation9,2010,27(11):1479-1488. 255. [9]ZHANG W J,XIE X F.DEPSO:hybrid particle swarm [21]王凌,李令莱,郑大钟,非线性系统参数估计的一类有 with differential evolution operator[C]//Proc of IEEE In- 效搜索策略[J].自动化学报,2003,29:953-958. ternational Conference on System,Man and Cybernetic. WANG Ling,LI Lingtai,ZHENG Dazhong.A class of ef- Washington DC,USA,2003:3816-3821. fective search strategies for parameter estimation of nonlin- [10]HE S,WU Q H,WEN J Y,et al.A particle swarm opti- ear systems[J].Acta Automatica Sinica,2003,29:953. mizer with passive congregation[J].BioSystems,2004, 958. 78:135-147. 作者简介: [11]秦全德,李荣钩.基于生物寄生行为的双种群粒子群算 秦全德,男,1979年生,讲师,博士,主 法[J1.控制与决策,2011,26(4):548552. 要研究方向为智能计算及其应用、管理决 QIN Quande,LI Rongjun.Two-population particle swarm 策与优化等发表学术论文10余篇. optimization algorithm based bio-parasitic behaviour[J]. Control and Decision,2011,26(4):548-552