
第8卷第2期 智能系统学报 Vol.8 No.2 2013年4月 CAAI Transactions on Intelligent Systems Apr.2013 D0I:10.3969/i.issn.16734785.201202001 网络出版t地址:htp://www.cnki.net/kcma/detail/23.1538.TP.20121116.1701.006.html 基于粒子滤波的未知环境下机器人同时定位、 地图构建与目标跟踪 伍明,孙继银 (中国人民解放军第二地兵工程大学指挥信息系统工程系,陕西西安710025) 摘要:为了解决机器人在未知环境下的目标跟踪问题,提出了一种基于粒子滤波的机器人同时定位、地图构建与 目标跟踪方法.该方法采用Rao-Blackwellized粒子滤波器对机器人位姿状态、标志柱分布和目标位置同时进行估计. 该方法中,粒子群的总体分布情况表征机器人位姿状态,而每个粒子均包含2类EKF滤波器,其中一类用来完成对 标志柱分布的估计,另一类用来完成对目标状态的估计,粒子的权值则由粒子状态相对于标志柱和目标状态2类相 似度共同产生.通过仿真和实体机器人实验验证了该方法的有效性。 关键词:Rao-Blackwellized粒子滤波;同时定位与地图构建;目标跟踪 中图分类号:TP242.6文献标志码:A文章编号:16734785(2013)02016809 Simultaneous localization,mapping and object tracking in an unknown environment using particle filtering WU Ming,SUN Jiyin (The department of commander information system,The PLA Second Artillery Engineering College,Xi'an 710025,China) Abstract:The proposed research paper examines a simultaneous localization,mapping,and object tracking meth- od.The examination was in part based on a particle filter that allows a robot to track an object in an unknown envi- ronment.This method utilizies the Rao-Blackwellized particle filting to estimate the pose of robot,landmarks distri- bution,and object position simultaneously.The general distribution of a particle swarm represents the pose of a ro- bot,and each particle includes two kinds of Extended Kalman Filter(EKF).One EKF estimates distribution of landmarks,while the other EKF estimates the state of the object.The weight of particle is determined by the combi- nation of two likelihoods,one is the likelihood between particle state and landmarks,and the other is the likelihood between particle state and object state.The results of the research indicate the valid robot experimentation and sim- ulation,confirm the proposed research approach is very effective. Keywords:Rao-Blackwellized particle filter;simultaneous localization and mapping;object tracking 机器人同时定位与地图构建(simultaneous lo-法3];2)基于Bayesain估计的方法,而基于 calization and mapping,SLAM)是指机器人在未知环 Bayesain估计的方法又主要分成基于扩展式卡尔曼 境下,根据传感器信息的迭代完成环境地图构造,并 滤波的方法46和基于粒子滤波的方法79] 同时对机器人位姿状态进行估计的过程,SLAM的 对于某些实际任务单凭传统的SLAM方法是无 难度在于准确的地图构建依靠于准确的机器人位姿 法解决的,例如未知环境下目标的跟踪任务、未知环 估计,而准确的机器人位姿估计反过来又依靠于准 境下机器人的围捕任务.这些任务要求机器人在未知 确的环境地图.对于这个“鸡生蛋,蛋生鸡”的问题 环境条件下完成对目标的追踪,与传统目标跟踪问题 主要存在2类解决方法:1)基于扫描点匹配的方 不同,传统的目标跟踪问题往往假设系统准确知道传 感器的状态,并在此基础上,通过Bayesain方法对目 收稿日期:2012-0202.网络出版日期:2012-11-16 基金项目:国家“863”计划资助项目(2006AA04Z258): 标状态进行预测和更新.而本文所研究问题的特点 通信作者:伍明.E-mail:hyacinth531@163.com. 有:1)传感器的移动性和运行环境的未知性.在目标

第2期 伍明,等:基于粒子滤波的未知环境下机器人同时定位、地图构建与目标跟踪 ·169 追踪的过程中,机器人需要始终保持与目标的追随关 在此基础上给出基于Bayesian估计的机器人同 系,也就是说,机器人在跟踪过程中保持运动状态,因 时定位、地图构建和目标跟踪理论描述.为了递归式 此存在机器人状态估计问题,而由于机器人事先并不 地得到机器人状态S,目标状态t,以及地图状态L 了解其运动环境,所以还需对环境特征状态进行估 的后验概率,应用条件概率的定义将5k、…、的 计,实际上这就是传统的SLAM问题;2)机器人状态 联合概率以S、、LM的条件概率进行扩展可得 和目标状态相关性.目标的状态估计是在机器人状态 p(s,Ln,zu)= 估计的基础上完成的,如果将两者分开进行那么就不 p(,p(u). (2) 能有效表示两者的相关性,进而影响最终目标估计的 准确性.由此可见,本文研究的问题是SLAM问题和 目标跟踪问题的耦合,如何设计一种一体化的估计算 环境特征 法正是本文的目的.Wang等o川首先对该问题进行 环境特征 了研究并提出一种基于扫描点匹配的解决方法,由于 观测 该方法采用的是ICP(iterative closest point)匹配算 机器人状 法,因此无法描述机器人和目标的不确定性和相关 态序列 机器人控 性,并且存在累积误差2] 制序列 1同时定位、地图构建与目标跟踪问 且标观测 题描述 目标状态 序列 假设机器人R以一定轨迹s=[s1S2…5] 图1 SLAMTO的Bayesain网络关系 运动,其在k时刻的状态为5k=[y是],并 Fig.1 A dynamic Bayesian network of SLAMTO 且运动环境中包含若干个固定标志点Lw= 类似地,以z。的条件概率进行扩展可得: [m1n,…1nn],标志点i对应的坐标为1= p(S)= [xy:],i∈{1,2,…,m.同时目标轨迹为 p(a4ls,4,Lw2,tp(s4,y|t,).(3) t=[tt2…],其在k时刻的状态为= 变换式(2)并将式(3)代入得: xy].设z=[z12…],为从观测开 始一直到k时刻机器人对于环境的观测值,在很多 p(s,4Lwlt,)=p4Lw之1,) p(zu) 应用场合该观侧值可以是角度和深度信息.那么 p(a4ls,4,Lw2,t)p(s,4,Lwl2-,) SLAMTO(simultaneous localization and mapping with p(zu) tracking of objects)问题等同于求式(1): p(zst,Lv)p(s,Luu) p(S:,L,tI z,u). (1) p(zu) (4) 也就是说,要通过观测值z=[zz2…2.]和机 式(4)为SLAMT问题的Bayesian估计描述,其 器人的控制量4=[4142…k]来确定机器 中p(z.lsk,t,L)表示观测值的相似度(likehood), 人的状态S,标志点的位置LM以及目标的状态t. 用于对预测概率分布的矫正;p(zz-1,4)为归一 该过程实际上可以描述成为动态Bayesain网络,如 化系数,p(s,t,Luz-1,)是对机器人状态、目标 图1示.图1中节点表示动态系统中各部分在时间 状态和地图的预测概率分布, 序列中的状态,k代表时刻,箭头表示各状态的依赖 下面介绍式(4)分子部分第2项p(5k,t, 关系.从该图可知目标k时刻的观测值:依赖于机器 Lwz-1,)的推导.利用全概率公式用sk-1和tk- 人k时刻的状态S以及目标k时刻的状态k: 对该式变换可得: 因此利用该观测值可以估计机器人和目标的状 p(St,t,Lul,u)= 态;对于标志柱斥时刻的观测值依赖于标志柱的 p(ss14e,4a1,Lwlt-l,d)ds1d业1…(5) 位置1n(i=1,2,…,m)以及机器人k时刻的状态,因 此同样能够利用该值估计机器人状态和标志的位置。 利用条件概率定义,用sk-1,-1和Lw对式(5)进行

·170. 智能系统学报 第8卷 展开可得 p()=p()dsd= 2(2()dsd (6) 第项 第项 式(6)中已经体现出递归式估计过程,其中积 p(st,t,Lul z",u")= 分中第2项代表了k-1时刻得出的联合后验概率 p(sp(Ip(I). 密度.为了得出最终的预测概率密度还需计算式 (6)中第1项p(s,z-1,W,k-1,在-1,Lw),该项代表 (9) 了机器人状态和目标状态的联合概率密度从k-1到k 也就是说该问题能够分解成为一一个对机器人状 时刻发生的变换,以下分2种情况进行讨论。 态的后验概率估计问题,一个对目标状态的后验概 1)当机器人状态和目标状态不相关的情况,此 率估计问题以及对m个标志柱位置的估计问题,该 时有 结论是本文所用方法的基础, p(s,4lz-,d,-1,,Lw)= 重写式(9)如式(10)所示: p(SI S-,u)p(tt,u). (7) p(s,t,Lyzu)= 从式(7)可知,机器人和目标状态的联合概率 p(slt,)4ls大,)Πp(Is大,) -N(wT(-》:Q级 密度变化为机器人状态变化和目标状态变化的乘 -N(Im:i-i.k-1) 积,两者之间并没有相互作用. (10) 2)当机器人状态和目标状态相关时有 即目标和标志柱服从Gaussian分布,因此可以 p(st,tyl z,u,st-,tt-,Ln)= 用EKF对它们进行估计,本文利用粒子滤波完成对 p(s4lt-,t,-1,4-,4e,Lw)p(elz-1, 机器人状态p(sz,)的估计.为了完成标志柱和 目标的估计,算法对每一个粒子所对应的标志柱 u,Sg-l,t-l,Lw)d止-l= p(1ms,z,)和目标状态p(tlst,z,)运用 p(sls-1,W,l)p(al1,t)d此…(8) EKF进行估计,其中s表示第i个离子在k时刻所 式(8)由全概率公式得出,表示了机器人状态变化 代表的机器人状态,因此假设离子总数为N,观测 受到了k-1时刻目标状态的影响,这种情况体现在现 到标志点个数为L,目标个数为1,则算法总共包含 实中为机器人不光要跟踪目标同时还需要尾随目标的 N,×(L+1)个EKF. 情况.下面介绍解决SLAMTO问题的具体实现方法, 首先,构造粒子群如下: 2基于Rao-Blackwellised粒子滤波器 =,i222-指 式中:S表示k时刻第i个粒子的位置其表示的机 的SLAMTO实现 器人的状态,u2和,2分别表示第i个粒 2.1问题的因式化表示 子k时刻已发现的1|个标志点位置的均值和方 如图1所示,如果知道机器人的路径s“= 差,和表示k时刻第i个粒子对应的目标状 [s:2…S],那么时间序列上的观测值z”= 态均值和方差.那么最终构造出的k时刻粒子群结 [z2… ,]将是相互独立的.那么式(1)能够进 构如图2所示 行因式化,如式(9): 机器人状念 日标状态 路标1 路标L 粒子1: [xty:0:]T [4T LwE公 粒子2: [x贤]T Lu Lu L4421 粒子N: S [:]T LL [u L吃' 图2粒子结构示意 Fig.2 Structure of each particles

第2期 伍明,等:基于粒子滤波的未知环境下机器人同时定位、地图构建与目标跟踪 ·171· 2.2粒子权值的计算 阵,为式(12)对t的雅克比阵在s和t处的值,即 下面介绍粒子权值的计算,粒子权值相当于该 粒子对应观测值的相似度,即 w=p(zk|S2,k,乙g-1,4)= (-2+-y.-3-y 0 -x0 p(24乙n|52,4%,2k-1,4s)= 类似,可以计算出p(Is) p(1S,zk-1,)p(z|S,4,3k-1,) 2.3目标和标志柱均值和方差的计算 Mankoy p(zn,1S,乙-1,us)= 接下来介绍目标点状态的估计,基于单个粒子 p(zI s)p(zI si,t)p(zm I s) 目标点状态估计可表示为 p(I s)p(z). (11) p(41s,)g 式中:,之之,分别代表对已知标志柱、目标和新标 ap()p() 志柱的观测值,‘为预测阶段根据EKF得到的目标 p(as14,)p(1s,,w) 状态(参见下2.3节内容),而p(zm,Is)认为是均匀 p(a1,4)p(,l5克,,wm 分布的,因此最终权值可表示为标志柱观测值相似 度和目标观测值相似度之间的乘积.以下具体介绍 p(zs1si,4)p(e1t-1,s,z-l, 目标观测值相似度p(z,Is,)的计算, dp(4l,2,)1 假设机器人的观测值为距离和角度信息,则机 2(zs)p(1,4)p(l1之,)d出- 器人对目标的观测模型: 更新阶设 预碳阶没 √(x-x)2+(y-y)7 (15) z4=h(s,)= argtan( 式中:α为归一化系数,s为k时刻第i个粒子状态 -0 √(x-x)2 式(15)可以应用EKF进行估计,EKF分为预测和更 (12) 新2个阶段,分别介绍如下 式中:s=[xRyR0]T表示机器人的状态量,t= 2.3.1EKF预测阶段 [xy8]T表示目标的状态量,d和0分别为机器 本文假设目标以恒速u=[vw]T运动并且u 人的观测值. 上存在协方差为Q”的误差(这里假设目标的运动 假设观测值相似度服从正态分布p(z)~N(, 为单模态形式,多模态运动形式将是今后研究的目 ),则相似度函数p(z,Is,)(为了简洁表示省去上 标).并且目标运行遵循差动驱动模型,即非完整性 标和下标)如式(13): 约束模型: p(zI s,t)= ti=g(ti,uk)= 2mp(-2g-i))g-p》 -1 k·△t·co8(0k-1+△t·wx)7 yi-1 g·△t·sin(0k-l+△t·ws) (16) (13) 0k1 △t·①k 式中:为根据该粒子表示的机器人状态s和预测目 式中:△t为输人的间隔时间.从式(16)可见,目标在 标状态t由式(12)得到的预测观测值,乙:为实际的观测 k时刻的不确定性由2部分组成,1)是由k-1时刻 值,号为观测值的协方差矩阵,下面介绍的计算. 的不确定性传播而来,记作-1;2)是由输人量的 协方差阵反映对目标观测值的误差情况,这 不确定性Q传播而来,记作.则根据误差传播公式 种误差由三方面造成,首先是传感器本身的误差,设 可以得到k时刻的预测误差协方差阵为 其值为R“;其次是由目标状态不确定性引起的误 残=+”= 差,设其值为R;最后为机器人状态不确定性引起 H-1(H)T+HQ(). (17) 的误差,由于这里用粒子群来代表这种不确定性,因 式中:H"为式(16)对于输人4的雅克比阵在4s和 此对于单个粒子来说,认为机器人状态不存在误差。 -1处的值,H为式(16)对于机器人状态t的雅克 最终表示如式(14): 比阵在k和1-1处的值,即 =R+Rm=H()T+Rm.(14)》 H=08 式中:为预测阶段由EKF得到的目标状态协方差 d让,4-1三

·172· 智能系统学报 第8卷 「·cos(04+·)-·△2·sin(04+△·)门 13)F5.≠0 d·sin(0+·)4··cos(0:+·4) 14)ww =p(nIs)p()() 0 15)iJ=EKFCi =g. 16)ENDIF 17)0=0·0w T10-vk·△t·sin(0-1+△t·we)1 18)Fzm,≠☑ 01tk·△t·cos(0-4+△·) L00 1 I9)[i2-,'元2,.」=ADD_LANKMARK 2.3.2EKF更新阶段 ([iaa2i24]) 在每一次迭代过程中若机器人没有发现目标, 20)ENDIF 即目标的观测值为空时,那么EKF只进行预测,其 21ELSE 结果是目标的不确定性将不断增大.当机器人发现 22)[ui2-n2i2-a,]=[n2h12i2hn1 目标时,EKF将利用观测值对目标的均值和方差进 23)ENDELSE 行修正,而减少目标的不确定性, 24)ENDFOR 假设由预测阶段已经得到目标均值和方差为 25)ENDIF 和,而实际观测值为乙,则EKF对均值和方差 26)IF Resample_condition_satisfy 的更新为 27)[{,,2-,2a]=RESA- i=ui+Kkaiman (z Hui), MPLE[ 花=(I-Kkaim H') (18) 28)ENDIF 式中:Kkdman为卡尔曼系数其值,Kamn= 其中1)~5)是预测阶段(prediction step),首先 ()T(H()T+Rm)1,Rm为传感器误差 根据机器人状态转移方程对粒子进行预测撒点(粒子 协方差阵。 滤波形式),之后对该粒子中对应的目标状态均值和 单个粒子标志柱位置估计也同样能够用相似的 方差利用目标的状态转移方程进行预测(EKF预测 方式进行描述,不再赘述, 阶段式(16)和(17),此时的预测结果是存在误差的, 2.4 SLAMTO算法 算法主要思想是对整个粒子群应用粒子滤波进 当有观测值出现,算法进入修正阶段,即6)~24),主 行重要性采样及重采样,而在每个粒子中又应用 要包括:根据式(11)进行的粒子权值的更新,目标状 EKF对标志柱及目标的均值和方差进行预测和校 态和标志柱位置的更新.具体来讲,第8)行运用数据 正操作,具体算法如下。 关联方法将观测值2区分为江,2,(分别表示对 [{i,ui2-a,}]= 标志柱、目标、新标志柱的观测值),而Table则包含 PFSLAMT[-12山2a马a--格] ,和已知标志柱的对应关系,需要注意的是每个粒子 i均拥有自己的k时刻环境地图1,2,…,1m,并根据 1)F0Ri=1:N, 2)s是~p(sxls话-1,x), 该地图进行数据关联.9)~12)行利用z4,和式(11)对 3)=g(,4), 粒子权值进行更新,并根据式(18)用EKF对目标的 4)=-1(H)「+酽Q(H), 均值和方差进行修正,类似地13)~16)行利用对 5)ENDFOR 粒子权值进行更新,并用EKF对已知标志柱均值和 6)IFz%≠☑ 方差进行修正,需要注意的是当观测到多个已知标志 7)FOR i=1:N, 柱时粒子权值等于其对应的每一个相似度(likehood) 8)[Table =Data-association 的乘积.17)行根据式(11)生成最终的粒子权值.18) [n.2-h2i2.mh]) ~23)行完成对于标志柱地图的更新.26)~27)行利 用文献[13]介绍的方法对粒子群进行重采样。 9)Fz,≠0 10)wi=p() 3实验结果 11)[u]=EKFUPDATE() 下面首先通过仿真实验从定位准确性、粒子数 12)ENDIF 量和标志柱数量对定位的影响三方面来验证算法的

第2期 伍明,等:基于粒子滤波的未知环境下机器人同时定位、地图构建与目标跟踪 ·173· 有效性,仿真是在Matlab7.0环境下进行的,假设环 651 境中包含若于个标志柱、一个机器人以及一个目标. 650 为了减少问题的复杂性,假设环境中不存在障碍物, 6.49 机器人能够感知一定范围内的目标和标志柱,并且 获得以方向和深度为表征的观测值.另外,机器人会 =648 根据目标位置调整输入使其能够追踪目标,而目标 647 速度及角速度控制量为恒定值, 6.46 3.1实验1 假设环境为10×10m2,其中均匀分布着20个 645249咖5咖6927922妙909892 标志柱,算法采用的粒子数为200,并假设机器人速 (d)区域3标志柱粒子 度和角度控制噪声方差阵为diag(0.4m, 4.95m 0.0872rad).目标速度和角度控制噪声方差阵为: 494 diag(0.8m,0.6rad),观测的误差协方差阵为:diag 493 (0.12m,0.0082rad,仿真实验迭代320次并且假设 4.92 8次迭代发生1次观测,这样的实验共进行了20 4.91 次,其中一次实验结果场景如图3所示 4.90 7 区域 489 48 6 且标轨迹 6.806.82 6.846.866.886.90 ,父域1 域4 (e)区域4目标位置 图3.SLAMTO仿真结果 2日、标志柱 Fig.3 Simulation results of SLAMTO 机器人轨迹 图3中,星点代表标志点的实际位置,以下结论 1 区域2 是在多次仿真基础上得出的,运用一次仿真结论只 2 3 45678910 是为了说明方便.由于观测频率相对于环境更迭频 率较慢(1:8),运动噪声较大以及机器人定位误差 (a)仿其结果 的传播导致目标定位误差大于机器人定位的误差 5.35 (误差均值0.0393,误差均方差0.0136),尽管如 5.30 此,对目标的定位仍比较准确(误差均值0.0639, =.5.25 误差均方差0.0104).图3(b)~(e)是特定区域的 5.20 放大图,其中图3(b)、(e)中粒子群代表对机器人 5.18 8.2 8.3 8.4 8.58.6 和目标的位置估计,图3(c)、(d)中粒子群代表对 应标志柱的估计值,要注意的是图3(b)、(e)中和 (b)区域1机器人位置 图3(c)、(d)中的粒子是对的,即图3(b)、(e)中粒 0.125r 子是s,中对应的S和u分量,而图3(c)、(d)中 粒子是3:中对应第3个和第12个标志柱的均值分 0.1204 量.图3(b)、(e)中由于重采样的作用代表机器人 和目标位置的粒子群分布集中并且多数粒子分布重 .0.115 合,因此粒子群分布能够代表机器人和目标的位置, 对于图3(d)来说所有粒子均重合,这同样是重采样 0.1104 的结果,因为对于该标志点的观测早已发生,在跌代 的过程中误差较大的粒子逐步被误差小的粒子取 0.105 1.555 1.560 1.5651.5701.5751.580 代,最终只有早期单个离子对应的该标志点位置估 计保留下来.而图3(c)中对应标志点的粒子群较为 (c)区域2标志柱粒子 分散,这是因为该标志点刚刚发现,重采样过程还没
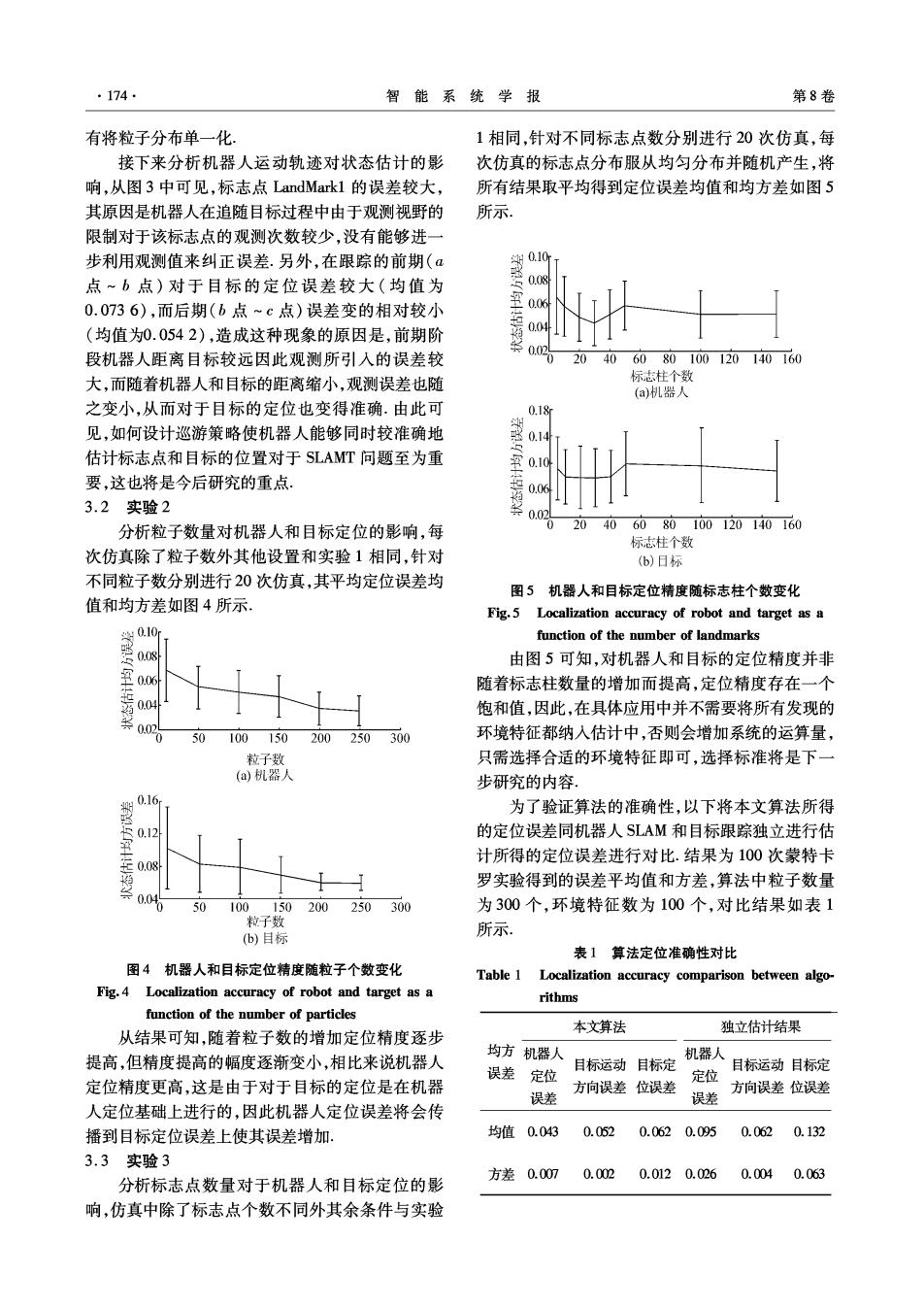
·174 智能系统学报 第8卷 有将粒子分布单一化 1相同,针对不同标志点数分别进行20次仿真,每 接下来分析机器人运动轨迹对状态估计的影 次仿真的标志点分布服从均匀分布并随机产生,将 响,从图3中可见,标志点LandMark1的误差较大, 所有结果取平均得到定位误差均值和均方差如图5 其原因是机器人在追随目标过程中由于观测视野的 所示 限制对于该标志点的观测次数较少,没有能够进一 步利用观侧值来纠正误差.另外,在跟踪的前期(α 点~b点)对于目标的定位误差较大(均值为 0.0736),而后期(b点~c点)误差变的相对较小 0.06 (均值为0.0542),造成这种现象的原因是,前期阶 0.04 段机器人距离目标较远因此观测所引人的误差较 20406080100120140160 大,而随着机器人和目标的距离缩小,观测误差也随 标志柱个数 (a)机器人 之变小,从而对于目标的定位也变得准确.由此可 0.18 见,如何设计巡游策略使机器人能够同时较准确地 0.14 估计标志点和目标的位置对于SLAMT问题至为重 0.10 要,这也将是今后研究的重点. 0.06 3.2实验2 分析粒子数量对机器人和目标定位的影响,每 020 406080100120140160 标志柱个数 次仿真除了粒子数外其他设置和实验1相同,针对 (b)日标 不同粒子数分别进行20次仿真,其平均定位误差均 图5机器人和目标定位精度随标志柱个数变化 值和均方差如图4所示, Fig.5 Localization accuracy of robot and target as a function of the number of landmarks 0.08 由图5可知,对机器人和目标的定位精度并非 随着标志柱数量的增加而提高,定位精度存在一个 0.04 饱和值,因此,在具体应用中并不需要将所有发现的 50100150 200250 300 环境特征都纳入估计中,否则会增加系统的运算量, 粒子数 只需选择合适的环境特征即可,选择标准将是下一 (a)机器人 步研究的内容 0.16 为了验证算法的准确性,以下将本文算法所得 0.12 的定位误差同机器人SLAM和目标跟踪独立进行估 计所得的定位误差进行对比.结果为100次蒙特卡 0.08 罗实验得到的误差平均值和方差,算法中粒子数量 0.04 50100150200250 300 为300个,环境特征数为100个,对比结果如表1 粒子数 (b)目标 所示 表1算法定位准确性对比 图4机器人和目标定位精度随粒子个数变化 Table 1 Localization accuracy comparison between algo- Fig.4 Localization accuracy of robot and target as a rithms function of the number of particles 本文算法 独立估计结果 从结果可知,随着粒子数的增加定位精度逐步 提高,但精度提高的幅度逐渐变小,相比来说机器人 均方机器人 机器人 误差定位 目标运动目标定 目标运动目标定 定位精度更高,这是由于对于目标的定位是在机器 方向误差 定位 位误差 误差 方向误差位误差 误差 人定位基础上进行的,因此机器人定位误差将会传 播到目标定位误差上使其误差增加, 均值0.043 0.052 0.0620.095 0.062 0.132 3.3实验3 方差0.007 0.002 0.0120.026 0.0040.063 分析标志点数量对于机器人和目标定位的影 响,仿真中除了标志点个数不同外其余条件与实验

第2期 伍明,等:基于粒子滤波的未知环境下机器人同时定位、地图构建与目标跟踪 ·175· 从表1可见,本文设计算法在机器人定位精度 上与独立估计结果基本相同,但在对目标的定位精 度上却明显高于后者,这是由于算法在进行状态估 计时,将机器人和目标状态作为估计整体,从而引入 了机器人和目标的相关性,使对目标的状态估计更 加准确。 最后将利用2台Pioneer3DX实体机器人验证 该方法的实用性.实验环境如图6(a)所示,机器人 R,和目标机器人R2均以直线轨迹穿过布满标志柱 的环境,为了检测到目标机器人(R2),对其用色块 进行标注.当R,检测到R2时将根据方向信息并利 -13.0-125-12.0-115-110-105-1009.5 用激光扫描仪返对R2的深度和角度观测值.图6 (b)显示了利用本文方法得到的R,和R2的运行轨 (d)轮盘编码器定位扫描点分布 迹以及扫描点的分布图. 图6实体机器人实验结果 Fig.6 Results of real robot experiment 图6(©)显示了得到的标志柱不确定性分布和 R,R2的轨迹图.图6(d)显示了只用轮盘编码器得到 的结果图,对比图6(b)和图6(d)可见,运用本文设 计方法得到的扫描点分布的一致性明显优于只用轮 盘编码器进行定位的结果. 4结束语 (a)实验环境 本文针对机器人同时定位、地图构建与目标跟 踪问题提出了一种基于粒子滤波的解决方法.该方 法的特点在于将机器人SLAM和目标状态估计作为 整体进行粒子滤波估计,从而在系统状态估计过程 中引入了机器人状态、环境特征状态以及目标状态之 间的相关性,进而提高了目标状态估计的准确性.该算 法为解决更为复杂的机动目标跟踪问题铺平了道路, 并拓宽了传统SLAM的应用范围,使之能够应用到诸 如未知环境下机器人围捕、入侵检测等实际任务中. 参考文献: -13.0-12.5-12.0-11.5-11.0-10.5-10.0-9.5 [1]BESL PJ,MCKAY N D.A method for registration of 3-D (b)扫描点分布以及目标、机器人轨迹 shapes[J].IEEE Transactions on Pattern Analysis and Ma- chine Intelligence,1992,14(2):239-256. [2]FU L,MILIOS E.Robot pose estimation in unknown envi- ronments by matching 2D range scans[J].Journal of Intelli- gent and Robotic Systems,1997,18:249-275. [3]MINGUEZ J,LAMIRAUX F,MONTESANO L.Metric- based scan matching algorithms for mobile robot displace- ment estimation[C]//Proceedings of IEEE International Conference on Robotics and Automation.Barcelona:IEEE -13.0-125-120-11.5-11.0-10.5-10.0-9.5 Computer Society,2005:563-570. [4]CHATILA R,LAUMOND J P.Position referencing and (c)标志柱不确定性分布 consistent world modeling for mobile robots[C]//Proceed-

·176: 智能系统学报 第8卷 ings of IEEE International Conference on Robotics and Au- 26(9):889-916. tomation.St Louis,USA:IEEE Computer Society,1985: [11]WANG CC,THORPE C,THRUN S.Online simultaneous 138-145, localization and mapping with detection and tracking of [5]SMITH R,SELF M,CHEESEMAN P.A stochastie map for moving objects:theory and results from a ground vehicle in uncertain spatial relationships[C]//Proceedings of Interna- crowded urban areas[C]//Proceedings of the IEEE Inter- tional Symposium of Robotics Research.Santa Cruz:Uni- national Conference on Robotics and Automation.Taipei, versity of California,1987:467-474. China:IEEE Computer Society,2003:842-849. [6]SMITH R,SELF M,CHEESEMAN P.Estimating uncer- [12]BORRMANN D,ELSEBERG J,LINGEMANN K.Global- tain spatial relationships in robotics.autonomous robot vehi- ly consistent 3D mapping with scan matching[J].Robotics cles[M].New York:Springer-Verlag,1990:167-193. and Autonomous Systems,2008,56:130-142. [7 MONTEMERLO M,THUN S,KOLLER D,et al. [13]SANJEEV A,SIMON M,GORDON N.A tutorial on par- FastSLAM:a factored solution to simultaneous mapping ticle filters for online nonlinear/non-Gaussian Bayesian and localization[C]//Proceedings of the National Confer- tracking[J].IEEE Transactions on Signal Processing, ence on Artificial Intelligence.[S.1.]The AAAI Press, 2002,50(2):174-188. 2002:593-598. 作者简介: [8]MONTEMERLO M,THUN S,KOLLER D,et al. 伍明,男,1981年生,讲师,博士,主 FastSLAM 2.0:an improved particle filtering algorithm 要研究方向为自主机器人控制、多机器 for simultaneous localization and mapping that provably 人协作、机器人环境构建。 converges[C]//Proceedings of International Joint Confer- ence on Artificial Intelligence.Acapulco:The AAAI Pre93,2003:1151-1157. [9]HAHNEL D,WEGBREIT B,FOX D,et al.An efficient FastSLAM algorithm for generating maps of large-scale cy- 孙继银,男,1952年生,教授、博士 clic environments from raw laser range measurements[C]/ 生导师,国家“863”计划评审专家,二炮 Proceedings of IEEE/RSJ Interational Conference on Intel- 导弹技术专家,中国计算机学会高级会 ligent Robots and Systems.Las Vegas:IEEE Computer So 员,中国计算机用户协会理事.全军先 ciety,2003:206-211. 进教育工作者,享受国务院特殊津贴, [10]WANG CC.THORPE C.Simultaneous localization and 多项科研成果获全军科技进步奖.发表 mapping with detection and tracking of moving objects 学术论文70余篇. [J].Interational Journal of Robotics Research,2007