
第7卷第6期 智能系统学报 Vol.7 No.6 2012年12月 CAAI Transactions on Intelligent Systems Dec.2012 D0I:10.3969/i.issn.16734785.201205025 网络出版t地址:htp://www.cnki.net/kcma/detail/23.1538.TP.20121116.1702.010.html 从Parzen窗核密度估计到 特征提取方法:新的研究视角 刘忠宝12,王士同 (1.江南大学数字媒体学院,江苏无锡214122:2.中北大学电子与计算机科学技术学院,山西太原030051) 摘要:当前主流特征提取方法大致有2种研究思路:1)从高维数据的几何性质出发,根据某种寻优准则得到基于 原始空间特征的一组特征数更少的新特征;2)从降维误差角度出发,保证降维前后数据所呈现的某种偏差达到最 小.试图从降维过程中数据分布特征的变化入手,基于广泛使用的Parzen窗核密度估计方法,来审视和揭示Parzen 窗估计与典型特征提取方法LPP、LDA和PCA之间的关系,从而说明这些特征提取方法可统一在Parzen窗框架下进 行研究,为特征提取方法的研究提供了一个新的视角. 关键词:特征提取;Parzen窗;密度估计;数据分布特征;新视角 中图分类号:TP392文献标志码:A文章编号:16734785(2012)060471-10 From Parzen window estimation to feature extraction:a new perspective LIU Zhongbao2,WANG Shitong' (1.School of Digital Media,Jiangnan University,Wuxi 214122,China;2.School of Electronics and Computer Science Technology, North University of China,Taiyuan 030051,China) Abstract:Researches on current feature extraction methods are mainly based on two ways.One originates from geo- metric properties of high-dimensional datasets and attempt to extract fewer features from the original data space ac- cording to a certain criterion.The other originates from dimension reduction deviation and try to make the deviation between data before and after dimension reduction be as small as possible.However,there exists almost no study a- bout them from the perspective of the scatter change of a dataset.Based on Parzen window density estimator,we thoroughly revisit the relevant feature extraction methods from a new perspective and the relationships between Parzen window and classical feature extraction methods,ie length of perpendiculars(LPP),linear discriminant analysis (LDA) and principal component analysis(PCA)are built in this paper.Therefore,these feature extraction methods can be re- searched in the same Parzen window,which provides a new perspective for the research of feature extraction. Keywords:feature extraction;Parzen window;density estimation;data distribution characteristics;new perspec- tive 在实际应用中常常遇到高维数据,如多媒体数 过将原始特征空间低秩近似,保证降维后的特征非 据、文本数据、生物数据等.尽管高维数据比低维数 负;主成分分析(principal component analysis, 据拥有更多的信息量,但在实际操作中非常不便.一 PCA)[21通过对原始特征空间方差的研究得到一组 种有效的解决方法就是对其进行特征提取.所谓特 正交的主成分;奇异值分解(singular value decompo- 征提取是指原始特征空间根据某种准则变换得到低 iion,SVD)[3]通过考察奇异值的贡献率实现降维; 维投影空间的过程.近年来,研究人员提出众多特征 独立成分分析(independent component analysis, 提取方法(feature extraction methods,FEM):非负矩 ICA)[4同时利用原始特征空间的二阶和高阶统计 阵分解(non-negative matrix factorization,NMF)l通 信息,进一步提高了PCA的降维效率;线性判别分 析((linear discriminant analysis,LDA)[5通过最大化 收稿日期:201205-14.网络出版日期:2012-11-16. 类间离散度和类内离散度的广义Rayleigh熵实现特 基金项目:国家自然科学基金资助项目(61170122,61272210). 通信作者:刘忠宝.E-mail:liu_zhongbao@hotmail.com. 征变换;多维缩放(multi-dimensional scaling

.472 智能系统学报 第7卷 MDS)[6通过保持数据点间的相似性实现降维;局 a≥0,i=1,2,…,W 部线性嵌入(locally linear embedding,LLE)[利用 式中:K(x,x:)为窗宽为8的核函数,a:(i=1,2, 稀疏矩阵算法实现降维;拉普拉斯特征映射(Lapla- …,N)为系数.其中,核函数K必须满足: cian eigenmap)[8]利用谱技术实现降维;典型相关分 1)K(t)≥0; 析(canonical correlation analysis,CCA)9]利用综合 变量对之间的关系来反映2组指标之间的整体相关 2)K,(t)dt=1. 性;局部保持投影(locally preserving projections,. 常用的核函数有: LPP)[10通过保持原始特征空间内在的局部几何结 1)Gaussian核函数K(x,y)=exp(-‖x 构实现降维, y‖2/282),参数6>0. 在实际应用中,针对不同的应用场合,本课题组 2)多项式核函数K(x,y)=(x'y+c),c和d 提出若干改进算法:皋军等I利用Fisher准则中的 为参数.当c=1且d=0时,K(x,y)=x「y.此时多项 类内散度重新构造势支撑向量机的目标函数,提出 式核为线性核 广义势支撑特征选择方法(generalized potential sup- 3)Sigmoid核函数.K(x,y))=tanh(b(ry)+c), port features selection method,GPSFM),该方法具有 b(xy)>0,且c<0. 冗余度低、选择速度快等优点;王晓明等2]针对监 督的局部保持投影算法在小样本情况下矩阵的奇异 4)Epancbnikov核函数K(x)=名(1- 性问题,提出广义的局部保留投影算法(generalized su- pervised locality preserving projection,GSLPP),该方法 ),1xl≤1,d为参数。 2 有效地解决了小样本问题;王超等)提出有局部保持 Sigmoid核函数在特定参数下与Gaussian核函 的最大间距准则特征提取方法,该方法能使投影后的 数具有近似性能;多项式核函数参数较多,不易确 样本具有最大类间散度和最小类内散度,在解决小样 定,且当阶数d较高时运算可能出现溢出.因此本文 本问题的同时更好地保持人脸图像的局部流形结构. 重点关注Gaussian核函数和Epanechnikov核函数, 上述特征降维方法主要从空间几何和降维误差 它们均为最小均方差意义下的最优核函数.通过合 角度进行研究.从空间几何角度看,特征提取实质上 理的参数选择,它们可用于任意分布的数据 是根据一定规则最优化缩小特征空间的过程;从降 维误差角度看,特征提取的目的是保证降维前后数 2 Parzen窗与LPP 据的偏差尽可能小.目前大多数特征提取方法重点 大多数特征提取方法主要从空间几何和降维误 关注几何性质和降维误差,而对于降维过程中数据 差角度进行研究,而对于降维过程中数据分布特征 分布特征的变化往往重视不够.鉴于此,本文引入 的变化则关注不够.本文从降维过程中数据分布特 Parzen窗核密度估计表征数据的分布特征,通过分 征的变化入手,基于广泛使用的Parzen窗核密度估 析降维过程中数据分布特征的变化,揭示Parzen窗 计方法,通过探讨Parzen窗估计与典型特征提取方 估计与典型特征提取方法LPP、LDA和PCA之间的 法LPP、LDA和PCA之间的关系,进而说明这些特 关系,从而说明这些特征提取方法可统一在Parzen 征提取方法可统一在Parzen窗框架下进行研究.本 窗框架下进行研究,为特征提取方法的研究提供了 节首先讨论Parzen窗与LPP之间的关系 一个新的视角 设有样本X=[x12…xw]ER"xW,其中 1 Parzen窗 x(i=1,2,…,N)eRw表示第i个样本,N表示样 本总数 在统计学和其他相关领域,核密度估计备受关 2.1 LPP 注.Parzen、Silverman、.Rosenble等是当前主流的核密 度估计方法4.Parzen窗法具有优良性能5,因而被 LPP16在保持样本局部流形结构不变的基础上 广泛使用.本文采用Parzen窗表征数据的分布形状. 实现特征提取,即在高维空间的邻近样本点在低维 Parzen窗定义为 空间的相对关系保持不变.算法流程如下: 1)创建邻接图.如果样本点x:和£满足 p(x)=∑aK(x,x), ‖x-x‖2<e,则将两点相连; 2)计算权值.权值计算公式为 8.t. ,a=1, S=exp(-‖x-x‖2/e)

第6期 刘忠宝,等:从Parzen窗核密度估计到特征提取方法:新的研究视角 ·473· 3)求解投影矩阵W.W可通过最小化如下目标 函数得到: 降维过程中散度的变化速度用需表示。对 m∑(Wx-w)2s 式(1)求导可得 对上式进行代数变换有 、1 1 6=NV2m exp(-‖lx- 1∑(wx:-Wx,)Sg= 2行 xyI2/28)(1x:-xg12/-1). (2) 于xD,W-于wSW 针对某类数据降维,6已知.为了表示方便,将 N表示为N,6表示为6,去掉式(2)中常数项有 WX(D-S)XW WXLXW. 式中:D为对角阵,且Da=Sg,L=D-S 器-启-am(-I-p 约束条件为 (3) WXDXW=1. 令式(3)中x∈{训练样本},则式(3)变为 上述优化问题可转化为求解如下广义特征值 问题: 器-盒em(--P) XLXW AXDXW. (4) 式中:前d个最小非零特征值对应的特征向量构成 为了使降维后的数据尽量保持原始空间的分布 的投影矩阵W=[0102·0a] 2.2 Parzen窗与LPP的关系 特征,因此投影方向W应满足散度的变化速度弧 06 从概率密度角度看,特征提取过程可以看作是 最小,可得目标函数: 数据分布特征保持的过程.用Parzen窗表征数据的 min IWTWI. (5) 分布特征并保证降维前后数据分布尽量保持一致. Parzen窗可定义为 式中:T=启1-与cm(wr(--与/ ,()=N合五2mex 1 。exp(-‖x-gI2/28). 282)W),I=[11…1].向量1保证式(4)投 影后仍为标量.由于exp(-‖x:-x‖2/282)可以 (1) 反映样本点x:和x之间关系,因此为了计算方便, 式中:方差6,表明各类样本偏离其类中心的程度, 式(5)中T可简化为 方差6,也称为散度.在降维过程中,方差6,的变化 速度越小,则数据的分布特征变化越小.若数据服从 T=x:2exp(W(-Ilx 22)W). 1 高斯分布,图1中的G1和G2表明降维前后数据分 式(5)可转化为 布的变化情况.降维后的数据在一定程度上进行了 min I'W'TWL. (6) 缩减,因此散度有变小的趋势 由于1与W无关,因此式(6)可表示为 G min W'X'LXW. -G. 式中:S,=em(-1出-128),D.=2,1 D-S. D反映样本点x:附近的局部密度.D越大,则 x:局部密度越大.因此对其约束有 WXDXW =1. 基于上述分析,上述最优化问题可归纳为 min W'X'LXW, s.t.W'X DXW =1. (7) 图1降维前后数据分布变化 为了表述方便,将上述优化问题称为基于 Fig.1 The transformation of data distribution before Parzen窗的特征提取方法(feature extraction method and after dimension reduction based on Parzen window,FEMPW)

474 智能系统学报 第7卷 由LPP算法不难看出:当样本点x:和x满足 N- ‖x:-x‖2<e时,将2点相连并计算相应权重.当 类的样本均值为(i=1,2,…,c),则有x=N x∈{训练样本}时,令LPP的权重函数为 LDA的最优化表达式为 s=exp(-1x-2)/28). WSeW J(W)=max (11) √/2T8 w WSW 且满足 由拉格朗日乘子法可得:求解式(11)等价于求 上含盒 解一般矩阵SSg的特征值问题. -exp(-lx2)dx =1. 3.1.2最小误差解释 (8) 以二分类问题为例,从最小误差角度解释 式中:C为常数, LDA. 求解式(8)可得 1)用Bhattacharyya系数确定二分类问题的错 C=1/N(2Φ(ε)-1). 误率上界。 式中:a)=∫2n(-r2 由文献[18]可知,为了使二分类问题错误率上 界尽可能小,必须保证Bhattacharyya系数尽可能 对于任意给定的ε值,通过查表可求得④(e), 大.用JB表示Bhattacharyya系数,有 进而得到C值.当B→∞时,C=1/N,此时FEMPW Jn =-Inp(xI 0)p(1 @2)dx. 等价于LPP.也就是说,LPP是FEMPW的特例. 假设2类样本服从正态分布:xly=0~N(1, 3 Parzen窗与LDA和PCA 1),xly=1~N(u2,2)则有 LDAS)和PCA]是特征提取中最为经典和广 g:-,3含)-a,+ 泛使用的方法.针对于LDA和PCA,科学家们进行 了广泛研究并取得了众多成果.与已有研究思路不 1(+2)/2 (12) 同,本文主要贡献在于:1)出发点不同,目前已有研 究主要从空间几何和最小误差角度展开,而本文从 当1=2=Σ时,式(12)可转化为 降维过程中数据分布特征的变化入手对其进行探 。=g:-u)2:u月 讨;2)解释模型不同,目前已有研究主要基于空间 几何和最小误差2种解释模型,而本文通过Parzen 特别地,当=E时, 窗建立概率密度估计与LDA和PCA的关系,从概 h=g-4:-a, 率密度角度对其进行解释. 2)样本的最大似然估计. 3.1 LDA 最大似然估计函数可表示为 3.1.1几何解释 从几何角度看,LDA的目的是将高维特征降到 L(中12,∑)= 低维空间,保证在低维空间异类样本尽量分开,同类 logp(x中142,∑)= 样本尽量紧密: = 样本的类间离散度矩阵和类内离散度矩阵分别 l1ogp(x1w12,∑)p), 定义为 求导并令导数为零可得 SB=∑N,(E-E)(x-)T, (9) ∑=∑(x-u)(x:-4)1+ S,=合(5-0(5,-)(10) ∑(x:-2)(x-) 式中:xg∈R(i=1,2,…,c=1,2,…,N)表示第i 类中的第j个样本,N:表示第i类样本个数,c表示 式中:Σ是样本特征方差均值, 样本类别总数所有样本的均值一含:设第: 为了使错误率的上界和样本散度尽可能小,投 影方向W应满足

第6期 刘忠宝,等:从Parzen窗核密度估计到特征提取方法:新的研究视角 ·475· WSW J(W)=m阳xwSW 21x-x2 N- 式中: 82 ≤1- SB=(u2-1)(2-u1)T, 可得 S=(-u)(x-u4)r+ ∑NIE-x:I2 台 Ps(x)≤1- (16) 82 ∑(x:-w2)(x-42)月 为了表示方便,取式(16)的上界并求导可得 上述最优化问题可转化为求解S需S:的特征值 问题.同理,对于c(c>2)类问题,类间离散度矩阵 需=后-,=12 和类内离散度矩阵的定义分别同式(9)和式(10). 为了使降维后的各类样本尽可能隔开,因此投 3.2 Parzen窗与LDA的关系 本节从概率密度角度讨论Parzen窗与LDA的 影方向W应满足使得各类需最大去掉与6有关 关系.Epanechnikov核函数[9是在最小均方差意义 的常数项,则有 下最优的核函数之一.受Epanechnikov核函数的启 max IW'S,WL. (17) 发,采用如下核函数进行密度估计: 式中:Sa=含Nx-I 2x)=1-合*-出2合x-41 由于式(17)中1与W无关,则有 ≤1. 8 6 max WiSeW, (18 (13) 综合式(15)和式(18)可得 为了计算散度的变化速度,对式(13)求导可得 W SeW 器=最1-,=12… J(W)=max ws.W 3.3 PCA 针对某类数据降维,则8已知.当x∈{训练样 3.3.1几何解释 1 本时,则=N,i=12,…6. 从几何角度看,PCA通过计算方差来衡量样本 包含信息量的大小.PCA称方差较大的分量为主成 为了保证降维前后数据分布的稳定性,因此投 分,主成分反映了原始变量的主要信息, 影方向W应满足使得职最小.去掉与ò有关的常 设投影方向为W,为了使投影后样本的总体离 08 散度最大,由方差的定义可得 数项,则有 1 ∑(x-)W)2= min Iw∑‖xg-x2wm. (14) J(w)=mxN 式中:向量1保证式(14)为标量.式(14)中1与W x1之w(x:-(x-E)W= mgxN 无关,并综合考虑各类样本,可得 min W'S,W. (15) gm(哈含红--用w 式中,=名- 令S=名(出-)x-到,则上式变为 下面求类间离散度矩阵Sg,对式(13)进行如下 J(W)=maxW'S,W. 数学变换: W可通过求解如下特征值问题得到: c Ni S,W =AW. Ps(x)=1-台台 82 3.3.2最小误差解释 设样本点:降维后变为x',希望降维后的样 ∑INe-xI2 1、 本点与原样本点之间的误差尽可能小,则引入最小 8 平方误差:

·476: 智能系统学报 第7卷 1-x 假设降维后的样本点x。代表所有降维后的样 P(x)=1-白 1,- 62 (22) 本点: 对式(22)求导可得 6x)-含6-P 0=2=1,2,…,N 0 82 含1%国-g国: 去掉与6有关的常数项有 线 =1-x12, 08 为了保证PCA提取出的主成分包含尽可能多 含-2含偶-+ 的信息,因此投影方向W应保正所有样本的职尽 d6 言--含+含k 可能大.基于上述分析可得: maxI严W"SWI.. (23) (19) 式(19)第2项与x。无关,可看作常数,因此最小化 式中:S=‖x-x‖2(i=1,2,…,N),向量1保证式 (23)为标量,I与W无关综合考虑各类样本,可得 J(x)有x0=x,即x为样本均值 设降维后的样本点可表示为 max W'S,W. (24) x'=aW +x. (20) 式中,=名1 式中:a是x'到x的距离. 式(24)可转化为求解特征值问题,则投影方向 将式(20)代入式(19)有 W由S,的特征向量组成。 N 1(a1,a2,…,aw,W)=∑x'-2= 4 实验分析 兰1aw+到-x2=言4w-(- 为了进一步考察Parzen窗与主流特征提取方 含1wT-2宫4w4-9+兰k- 法的关系,分别在人工数据集和人脸数据集上对算 法进行测试.实验的基本流程如图2所示。 由‖W‖2=1,对a:求导并令导数为零,有 a:=W(x-x). 数据集 固定a,对W求偏导,并将上式代入J1有 J1(a1,a2,…,aw,W)= 训练样本 测试样本 含1w1-2宫w·宫- 学习训练 FEM (w(-P+合1- 输出 - 输人 投影方向 投影 2(w-x-w+立-2 投影后的 测试样不 -wSw+∑Ix-x‖2. 式中:S=(-)(x-x) 最近邻分类器 由于‖W‖2=1,引入拉格朗日乘子法可得 识别结果 S,W =AW. (21) W可由式(21)求得. 3.4 Parzen窗与PCA的关系 图2实验流程 Fig.2 The process of experiments 针对某类数据降维,令x:=x.则式(13)可变为
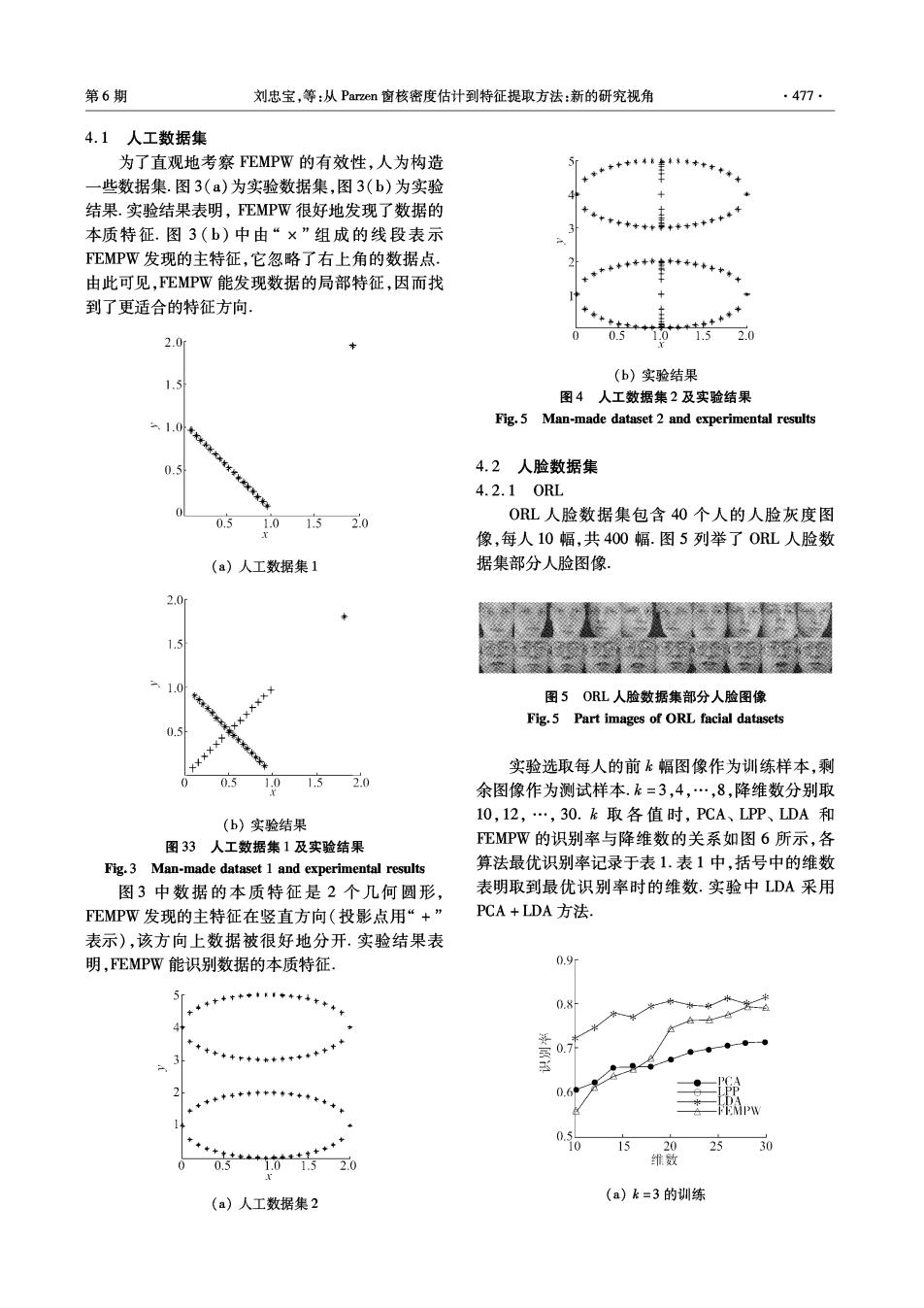
第6期 刘忠宝,等:从Parzen窗核密度估计到特征提取方法:新的研究视角 477. 4.1人工数据集 为了直观地考察FEMPW的有效性,人为构造 一些数据集.图3(a)为实验数据集,图3(b)为实验 结果.实验结果表明,FEMPW很好地发现了数据的 本质特征.图3(b)中由“×”组成的线段表示 FEMPW发现的主特征,它忽略了右上角的数据点. 由此可见,MPW能发现数据的局部特征,因而找 到了更适合的特征方向, 2.0 0.5 1.52.0 (b)实验结果 1.5 图4人工数据集2及实验结果 2.1.04 Fig.5 Man-made dataset 2 and experimental results 0.5 4.2人脸数据集 4.2.10RL 0.5 1.01.52.0 ORL人脸数据集包含40个人的人脸灰度图 像,每人10幅,共400幅.图5列举了0RL人脸数 (a)人工数据集1 据集部分人脸图像. 2.0 1.5 1.0 图5ORL人脸数据集部分人脸图像 Fig.5 Part images of ORL facial datasets 0.5 实验选取每人的前k幅图像作为训练样本,剩 0.5 1.0 1.52.0 余图像作为测试样本.k=3,4,…,8,降维数分别取 (b)实验结果 10,12,·,30.k取各值时,PCA、LPP、LDA和 图33人工数据集1及实验结果 EMPW的识别率与降维数的关系如图6所示,各 Fig.3 Man-made dataset 1 and experimental results 算法最优识别率记录于表1.表1中,括号中的维数 图3中数据的本质特征是2个几何圆形, 表明取到最优识别率时的维数.实验中LDA采用 FEMPW发现的主特征在竖直方向(投影点用“+” PCA+LDA方法, 表示),该方向上数据被很好地分开.实验结果表 明,FEMPW能识别数据的本质特征, 0.9r 5 08 0.7 2 0.5 0 1520 30 0.5 1.0+ 1.52.0 维 (a)k=3的训练 (a)人工数据集2

478. 智能系统学报 第7卷 1.0 0.9 0.91 0.8 0 0.7 0.6 *二FiPW 00 20 30 0.50 维数 15 20 2530 维数 (f)k=8的训练 (b)k=4的训练 图6ORL人脸数据集上各算法识别率与降维数的关系 Fig.6 Relation between recognition accuracy and re- duced dimension on ORL 表1ORL人脸数据集上各算法识别率 Table 1 Recognition accuracy of PCA,LPP,LDA and FEMPW on ORL 尺寸k PCA LPP LDA FEMPW 30.711(28)0.789(28) 0.814(30)0.789(28) 4 0.808(28) 0.867(30) 0.875(30) 0.867(30) 30 50.845(22) 0.890(24) 0.905(30) 0.890(24) 15 20 25 维数 6 0.863(22) 0.906(30) 0.950(30) 0.906(30) 70.892(20)0.917(22) 0.925(26) 0.900(22) (c)k=5的训练 80.873(20)0.925(30)0.938(26) 0.925(30) 平均0.8320.882 0.9010.882 1.0 由图6和表1可以看出:随着训练样本数的增加, 各算法的识别率基本呈上升趋势.当降维数较高时, 0.9 EPW具有优良的降维性能,甚至可以达到最优的识 别率.从平均性能看,EMPW的识别率明显高于PCA 且略低于DA,但亦能较好地完成降维任务.此外, FEMPW的降维效果等同于LPP,该实验现象与第2节 0.7 理论分析得到的“当&→∞时,FEMPW等价于LPP”结 0 论一致 10 15 20 2530 维数 4.2.2 Yale Yale人脸数据集共有15个人的人脸灰度图像, (d)k=6的训练 每人11幅,共165幅.图7列举了部分Yle人脸数 据集上的图像.Yale数据集中人脸的表情、光照等 1.0 变化比ORL数据集要快. 0.9 函0.8 图7Yale人脸数据集部分人脸图像 0.7 Fig.7 Part of Yale facial datasets 将Yale人脸数据集中每个人的前k幅图像作 00 20 25 30 为训练样本,剩下的图像作为测试样本.实验中= 维数 4,5,…,8,降维数分别取2,4,…,14.k取各值时, (e)k=7的训练 PCA、LPP、LDA和FEMPW的识别率与降维数的关
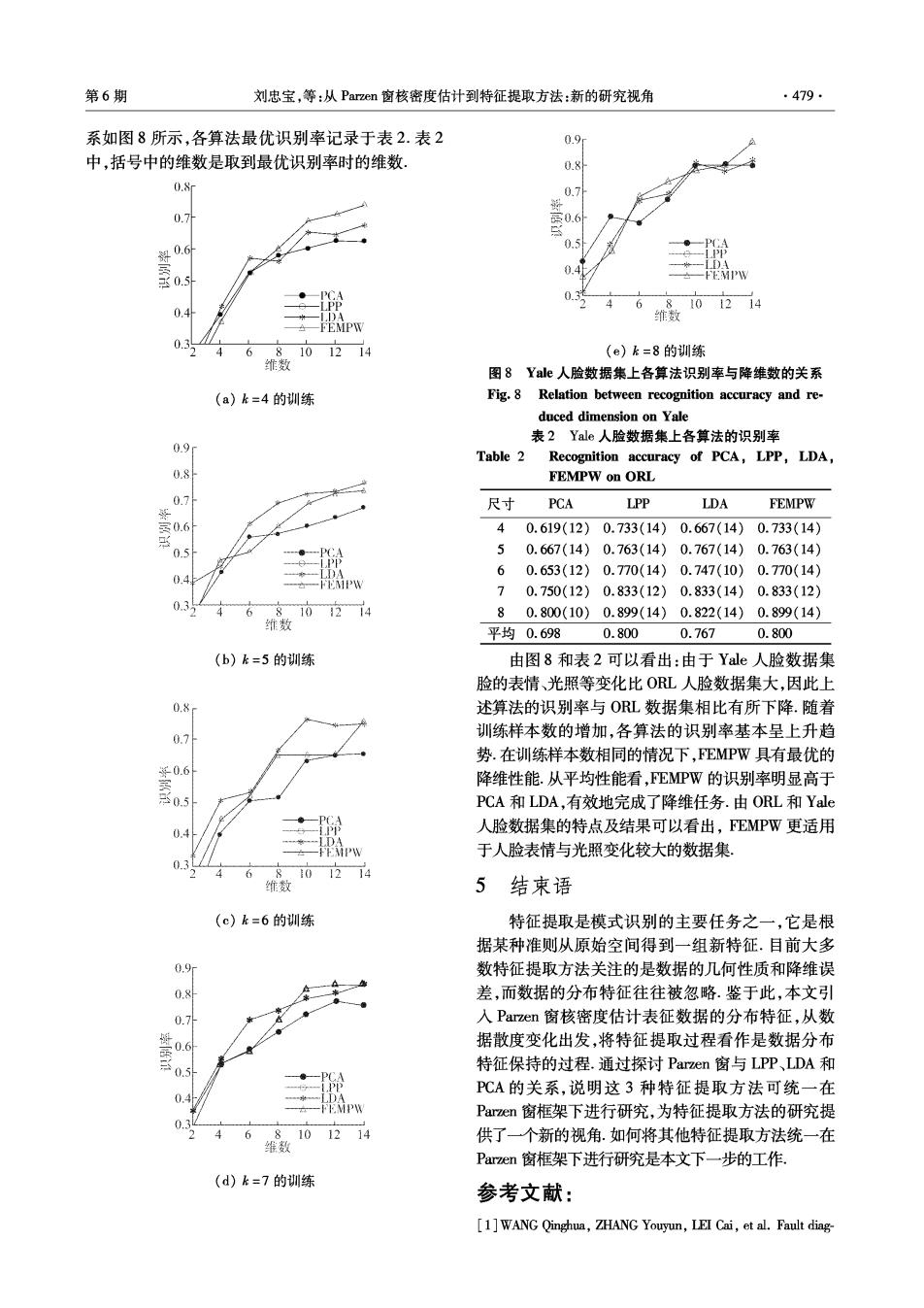
第6期 刘忠宝,等:从Parzen窗核密度估计到特征提取方法:新的研究视角 479 系如图8所示,各算法最优识别率记录于表2.表2 0.9 中,括号中的维数是取到最优识别率时的维数. 0.8 0.8 0.7 部06 宝a ●PCA -LPP 101214 0. *一LDA 维数 A—EMPW 6 ,810.1214 (e)k=8的训练 维数 图8Yle人脸数据集上各算法识别率与降维数的关系 (a)k=4的训练 Fig.8 Relation between recognition accuracy and re- duced dimension on Yale 表2Yale人脸数据集上各算法的识别率 0.9 Table 2 Recognition accuracy of PCA,LPP,LDA, 0.8 FEMPW on ORL 0.7 尺寸 PCA LPP LDA FEMPW 0.6 40.619(12)0.733(14)0.667(14)0.733(14) 8 0.5 50.667(14)0.763(14)0.767(14)0.763(14) 60.653(12)0.770(14) 0.747(10)0.770(14) 70.750(12)0.833(12)0.833(14)0.833(12) 6 802i4 80.800(10)0.899(14)0.822(14)0.899(14) 维数 平均0.698.0.800 0.7670.800 (b)k=5的训练 由图8和表2可以看出:由于Yale人脸数据集 脸的表情、光照等变化比OL人脸数据集大,因此上 0.8 述算法的识别率与OL数据集相比有所下降.随着 0.7 训练样本数的增加,各算法的识别率基本呈上升趋 势.在训练样本数相同的情况下,EMPW具有最优的 0.6 降维性能.从平均性能看,FEMPW的识别率明显高于 PCA和LDA,有效地完成了降维任务.由ORL和Yale 04 人脸数据集的特点及结果可以看出,FEMPW更适用 FEMPW 于人脸表情与光照变化较大的数据集。 8.0124 维数 5结束语 (c)k=6的训练 特征提取是模式识别的主要任务之一,它是根 据某种准则从原始空间得到一组新特征.目前大多 0.9 数特征提取方法关注的是数据的几何性质和降维误 0.8 差,而数据的分布特征往往被忽略.鉴于此,本文引 0.7 入Parzen窗核密度估计表征数据的分布特征,从数 0.6 据散度变化出发,将特征提取过程看作是数据分布 0.5 特征保持的过程.通过探讨Parzen窗与LPP、LDA和 P℃A的关系,说明这3种特征提取方法可统一在 0.4 Parzen窗框架下进行研究,为特征提取方法的研究提 0.3 6 8101214 供了一个新的视角.如何将其他特征提取方法统一在 维数 Parzen窗框架下进行研究是本文下一步的工作, (d)k=7的训练 参考文献: [1]WANG Qinghua,ZHANG Youyun,LEI Cai,et al.Fault diag-

·480. 智能系统学报 第7卷 nosis for diesel value trains based on non-negative matrix fac- WANG Chao,WANG Shitong.Maximum margin and lo- torization and neural network ensemble[J].Mechanical Sys- cality preserving feature selection method[J].Artificial In- tems and Signal Processing,2009,23(5):1683-1695. telligence and Pattern Recognition,2009,22(6):898- [2]CAMACHO J,PIC J,FERRER A.Data understanding with 902. PCA:structural and variance information plots[J].Chemomet- [14]ODIOWEI PP,YI Cao.Nonlinear dynamic process moni- rics and Intelligent Laboratory Systems,2010,100(1):48-56. toring using canonical variate analysis and kemel density [3]LIPOVETSKY S.PCA and SVD with nonnegative loadings estimations J].IEEE Trans on Industrial Informatics, [J].Pattern Recognition,2009,42(1):68-76. 2010,6(1):3645. [4]RADULOVIC J,RANKOVIC V.Feedforward neural net- [15]吴葛铭,霍剑青,王晓蒲.一种基于加权Parzen窗的聚 work and adaptive network-based fuzzy inference system in 类算法[J].中国科学技术大学学报,2002,32(5): study of power lines[J].Expert Systems with Applications, 546551. 2010,37(1):165-170. WU Geming,HUO Jianging,WANG Xiaopu.Weighted [5]PETER N B,JOAO P H,DAVID J K.Eigenfaces vs Parzen window based clustering[J].Journal of Chinease Uni- Fisherfaces:recognition using class specific linear projec- versity of Sciences and Technologies,2002,32(5):546-551. tion[J].IEEE Trans on Pattern Analysis and Machine In- [16]HE X F,YAN S C,HU Y X,et al.Face recognition u- telligence,1997,19(7):711-720. sing Laplacianfaces[J].IEEE Trans on Pattern Analysis [6]HU Y H,HE S H.Integrated evaluation method[M].Bei- and Machine Intelligence,2005,27(3):328-340. jing:Scientific Press,2000:27-31. [17]CAMACHO J,PIC J,FERRER A.Data understanding [7]ROWEIS S T,SAUL L K.Nonlinear dimensionality reduc- with PCA:structural and variance information plots[J]. tion by locally linear embedding[J].Science,2000(290): Chemometrics and Intelligent Laboratory Systems,2010, 2323-2326. 100(1):48-56. [8]BELKIN M,IYOGI P.Laplacian eigenmaps and spectral tech- [18]边肇祺,张学工.模式识别[M].2版.北京清华大学 niques for embedding and clustering[C]/Systems (NIPS). 出版社,2000:1-30. Cambridge:MIT NIYOGI P Press,2001:585-591. [19 ]GUO Q C,CHANG X J,CHU H X.Mean-shift of varia- [9]BORGA M,KNUTSSON H.Canonical correlation analysis ble window based on the Epanechnikov kemel[C]//Pro- in early vision[C]//Proceedings of the 9th European Sym- ceedings of IEEE Int Conf on Mechatronics and Automa- posium on Artificial Neural Networks.Bruges,Belgium, tion.Piscataway,USA,2007:2314-2319. 2001:309-314. 作者简介: [10]HE X F,NIYOGI P.Locality preserving projections[C]// 刘忠宝,男,1981年生,博士,主要 Advances in Neural Information Processing Systems 研究方向为模式识别、机器学习,发表 (NIPS).Vancouver,Canada,2003:153-160. 学术论文数十篇. [11]皋军,王士同,邓赵红.广义的势支撑特征选择GPS FM[J].计算机研究与发展,2009,46(1):41-51 GAO Jun,WANG Shitong,DENG Zhaohong.Generalized potential support vector machine for feature selection[]. Computer Research and Development,2009,46(1):41-51. [12]王晓明,王士同.广义的监督局部保留投影算法[J] 王士同,男,1964年生,教授,博士 电子与信息学报,2009,31(8):1840-1845. 生导师,主要研究方向为人工智能与机 WANG Xiaoming,WANG Shitong.Generalized supervised 器学习. locality preserving projection algorithm[].Electronics and Information,2009,31(8):1840-1845. [13]王超,王士同.有局部保持的最大间距准则特征提取 方法[J].模式识别与人工智能,2009,22(6):898- 902