智能系统：基于模糊控制与预测控制切换的翼伞系统航迹跟踪控制

第7卷第6期 智能系统学报 Vol.7 No.6 2012年12月 CAAI Transactions on Intelligent Systems Dec.2012 D0I:10.3969/i.issn.16734785.201205014 网络出版t地址：htp://www.cnki.net/kcma/detail/23.1538.TP.20121116.1701.008.html 基于模糊控制与预测控制切换的 翼伞系统航迹跟踪控制 李永新，陈增强，孙青林 (南开大学信息技术科学学院，天津300071) 摘要：以翼伞系统的六自由度模型为基础，针对翼伞系统的平面航迹跟踪问题，对已有的预测控制器进行改进，提 出模糊控制和广义预测控制相互切换的控制模式.利用横向轨迹误差法，在翼伞偏航角误差较大的情况下，采用模 糊控制，直至偏航角误差达到设定的较小范围内，切换为广义预测控制，对翼伞航迹进行精确的制导，在一定程度上 减少了处理器的运算量.采用真实的翼伞参数建立仿真模型，结果验证了这一控制方法的有效性。 关键词：翼伞；航迹跟踪；模糊控制；预测控制；切换 中图分类号：TP273.2文献标志码：A文章编号：1673-4785(2012)060481-08 Flight path tracking of a parafoil system based on the switching between fuzzy control and predictive control LI Yongxin,CHEN Zenggiang,SUN Qinglin (College of Information Technical Science,Nankai University,Tianjin 300071,China) Abstract:Based on the parafoil system model with six degrees of freedom,aim at the plane flight path tracking problem,the existing predictive controller is improved.A control mode is proposed,which switches between fuzzy control and generalized predictive control.According to the cross track error,when the yawing angle error of the parafoil is bigger,the fuzzy controller is applied until the error attains a small range that has been set.Then,the fuzzy control is switched to generalized predictive control,which can control and guide the parafoil in a higher pre- cise level.In this way,the operation of the processor can be reduced to a certain extent.A simulation model is built up based on an actual parafoil,and the final result demonstrates the validity of the control mode. Keywords:parafoil system;flight path tracking;fuzzy control;predictive control;switching 翼伞系统应用方式主要分为投放和回收.应用告等 领域包括3个方面：航空航天、军事领域和民用领 在自然灾害发生时，陆路交通被破坏、运输机无 域.在航空航天领域，翼伞系统可用于飞行器回收、 法着陆的情况下，翼伞系统用于物资投放，具有速度 无人驾驶机降落等过程，可降低对驾驶技巧的要求， 快、机动灵活的特性.以往使用的常规降落伞是无机 不必设计繁杂的着陆控制程序，并使飞行器在恶劣 动不可控的，执行飞行器回收和物资投放任务，伞体 的天气情况下同样能完成无损着陆.在军事领域，翼 飞行轨迹受风的影响，着陆偏差较大，实际系统偏差 伞系统可以用于物资、武器装备的精确投放，可以精 有时会达到几公里甚至是十几公里，使得搜救时间 确、高效、安全地将武力、物资投送到战场.在民用领 和回收成本大大增加).可控翼伞系统由于具有良 域，目前主要利用动力滑翔伞进行观光、航拍和广 好的滑翔性能和可操纵性23]，从而减少投放误差， 降低回收成本.美国著名的X-38计划将翼伞用于救 收稿日期：20120507.网络出版日期：2012-11-16. 基金项目：国家自然科学基金资助项目(61174094)：天津市科技支撑 生飞船在飞行最后阶段和着陆过程的自主归航，降 计划资助项目(09 ZCKFSF00500). 低了驾驶技术的要求4).经过多次试飞，验证了翼 通信作者：李永新.E-mail:new-liyx@gmail.com

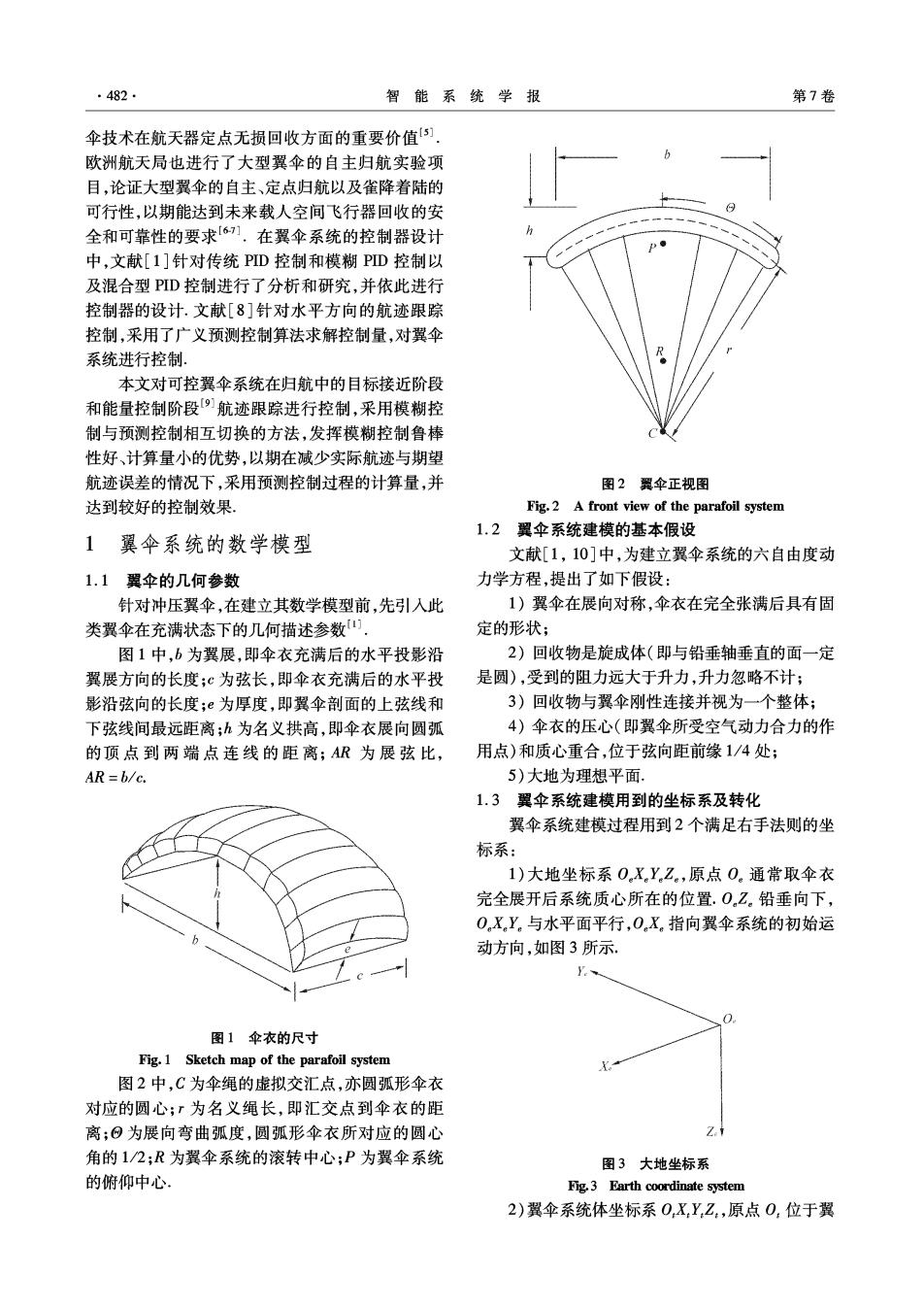
·482. 智能系统学报 第7卷 伞技术在航天器定点无损回收方面的重要价值例 欧洲航天局也进行了大型翼伞的自主归航实验项 目，论证大型翼伞的自主、定点归航以及雀降着陆的 可行性，以期能达到未来载人空间飞行器回收的安 全和可靠性的要求[6].在翼伞系统的控制器设计 中，文献[1]针对传统PID控制和模糊PD控制以 及混合型PID控制进行了分析和研究，并依此进行 控制器的设计.文献[8]针对水平方向的航迹跟踪 控制，采用了广义预测控制算法求解控制量，对翼伞 系统进行控制。 本文对可控翼伞系统在归航中的目标接近阶段 和能量控制阶段9)航迹跟踪进行控制，采用模糊控 制与预测控制相互切换的方法，发挥模糊控制鲁棒 性好、计算量小的优势，以期在减少实际航迹与期望 航迹误差的情况下，采用预测控制过程的计算量，并 图2翼伞正视图 达到较好的控制效果。 Fig.2 A front view of the parafoil system 1.2翼伞系统建模的基本假设 1翼伞系统的数学模型 文献[1,10]中，为建立翼伞系统的六自由度动 1.1翼伞的几何参数 力学方程，提出了如下假设： 针对冲压翼伞，在建立其数学模型前，先引入此 1)翼伞在展向对称，伞衣在完全张满后具有固 类翼伞在充满状态下的几何描述参数 定的形状； 图1中，b为翼展，即伞衣充满后的水平投影沿 2)回收物是旋成体（即与铅垂轴垂直的面一定 翼展方向的长度；℃为弦长，即伞衣充满后的水平投 是圆)，受到的阻力远大于升力，升力忽略不计； 影沿弦向的长度；为厚度，即翼伞剖面的上弦线和 3)回收物与翼伞刚性连接并视为一个整体； 下弦线间最远距离；h为名义拱高，即伞衣展向圆弧 4)伞衣的压心（即翼伞所受空气动力合力的作 的顶点到两端点连线的距离；AR为展弦比， 用点)和质心重合，位于弦向距前缘1/4处； AR =b/c. 5)大地为理想平面， 1.3翼伞系统建模用到的坐标系及转化 翼伞系统建模过程用到2个满足右手法则的坐 标系： 1)大地坐标系0.XY.Z。,原点0。通常取伞衣 完全展开后系统质心所在的位置.0.Z。铅垂向下， 0X。Y。与水平面平行，0X。指向翼伞系统的初始运 动方向，如图3所示. 图1伞衣的尺寸 Fig.1 Sketch map of the parafoil system X 图2中，C为伞绳的虚拟交汇点，亦圆弧形伞衣 对应的圆心；「为名义绳长，即汇交点到伞衣的距 离；⊙为展向弯曲弧度，圆弧形伞衣所对应的圆心 Z. 角的1/2；R为翼伞系统的滚转中心；P为翼伞系统 图3大地坐标系 的俯仰中心。 Fig.3 Earth coordinate system 2)翼伞系统体坐标系OXY,Z,原点O.位于翼

第6期 李永新，等：基于模糊控制与预测控制切换的翼伞系统航迹跟踪控制 ·483· 伞系统质心，OZ轴经过回收物质心，指向回收物. sin ytan cos ytan@ 0X,Z.为翼伞几何对称面，OX。指向伞衣前缘， 0 (3) 0Y,轴与其他两坐标轴构成右手系，如图4所示. -0 sin ycos cos ycos 式中：0.、0，、o:为翼伞系统在体坐标系下的角 速度， 0]r= [Au AB]F] LA2 A2M (4) 式中：F为翼伞系统所受力的总和，M为作用在翼 伞系统所有力矩总和，A:为真实质量和附加质量， A2为真实的转动惯量和附加转动惯量，A2=-A 为耦合项.可表示为 Au =m 13x3 ma, A2=L+Ln-Lǒ-pmLo-p, A2=-A21=-m.Lǒ-p 式中：I:为翼伞系统的真实转动惯量，I。为翼伞系统 的附加转动惯量，m,为翼伞系统的总质量（包括伞 图4翼伞系统体坐标系 衣、伞绳、吊带和空投物等)，m。为翼伞的附加质量， Fig.4 Coordinate system of the parafoil system I3x3为单位矩阵，L0-为旋转矩阵. 定义翼伞系统的3个姿态角：偏航角业、俯仰角 联立方程(1)~(4)求解，可得到翼伞系统的运 9、滚转角Y,分别指翼伞系统绕其体坐标系Z.轴、 动状态方程. Y.轴、X,轴转动所成的角度。 2翼伞系统航迹跟踪制导器 大地坐标系到体坐标系的转换矩阵可以表 示为 2.1航迹跟踪制导器的作用 T.-e=[t1t2t3]. (1) 翼伞系统的航迹跟踪可分为航向制导器和航向 式中： 控制器2部分. cos cos 航向制导器将翼伞系统的当前位置与期望的航 E1= sin ysin9cos业-cos ysin业 迹之间进行比较运算，计算出偏差，以调整翼伞系统 cos ysin cos sin ysin 的航向，从而消除航迹的偏差，使得翼伞系统的实际 cos sin 航向不断逼近期望航向。 2= sin ysin sin cos ycos, 2.2横向轨迹误差法 cos ysin Osin中-sin ycosψ 横向轨迹误差法，可根据自身位置误差不断调 sin 整，使受控对象达到期望的目标位置1.可做如下 t3= sin ycos 描述： cos ycos 定义(x,(),y,())与(x,(i-1),y,(i-1)分 1.4翼伞系统的运动方程 别为当前路径点和前一个路径点，(x(t),y(t)为 在文献[8]中，针对建立的翼伞系统运动方程， 翼伞系统当前位置.如图5所示. 有如下计算过程，当x、y、z为翼伞系统在大地坐标 风 系下的位置，、巴，巴：为翼伞系统在体坐标系下的速 △x=x,()-x,(i-1), 度，有 △y=y,()-y,(i-1), x=x,(i)-x(t), (2) y=y,(i)-y(t). 定义航迹线长度为第i-1到第i个路径点之间 并且 的距离，表达式如下：

·484 智能系统学报 第7卷 L:=√△x+△y. A(z)=1+a1z1+…+anz, (5) 轨迹跟踪误差△(t)为△(t)=（x△y-y△x)/ B(z1）=1+b1z1+…+bn2 L:;轨迹线航向角为也.(i)=tan-1(△y/△x);由轨迹 式中：n.和ns为翼伞系统需要辨识的阶数， 跟踪误差和轨迹线航向角得到期望输出航向角为 为得到y(k)的j步向前预测值y(k+),引入 中，(t)=△(t)+中(i);航向角跟踪轨迹误差表示为 式(6)的丢番图方程： 中.(t)=山，(t)-(),中(t)为翼伞系统当前航向 1=E(z1)A(z1)△+zE(z1), 角.这样把翼伞系统的轨迹跟踪问题转化为航向跟 j=1,2,…,N. (6) 踪问题 式中：E和F为待求多项式，并且有： aE;=j-1,oFj na, E,=e+eal+…+epr-w E=f力+2+…+fn&. 期望轨迹 严(x(i)y(i) 将式(5)两边同乘E,△z可得 E,A△y(k+j)= 实际轨迹 EB△u(k+j-1)+E(k+j). (7) (x(t)) 将式(7)代入式(6)得 (x(i-1)y(i-1) y(k +j)E BAu(k +j-1)+Fy(k)+ 图5翼伞系统实际轨迹与期望轨迹 E(k+). Fig.5 The actual and desired traces of the parafoil 得到未来输出y(k+)的预测值： y(k +jl k)E BAu(k +j-1)+Fy(k), 3翼伞系统航迹跟踪控制器 j=1,2,…,N. (8) 航向控制器用于控制翼伞系统的航向，使得翼 为将E,B△u(k+j-1)中已知信息和未知信息 伞系统在给定的航向指令下运动. 分离开来，引人式(9)丢番图方程： 3.1广义预测控制 EB=G+zH,j=1,2,…,N. (9)》 广义预测控制(generalized predictive control, 式中：G和H为待求多项式用递推算法可以解得E、 GP℃)是Clark等在1987年提出，采用了长时段的优 F、G、H,N为预测步长， 化性能指标，并结合辨识和自校正机制，表现出良好 目标函数为 的鲁棒性2]。 N 预测控制的主要特征是以受控自回归积分滑动 J=Σ[(k+j1)-ya(k+)]2+ 1 平均模型(controlled auto--regressive integrated mov- N。 A∑[△u(k+j-1)]2. (10) ing-average,CARIMA)为基础Ia),为了由k时刻的 输入、输出数据对（层+）时刻的系统进行预测，而引 式中：N。为控制步长，且N≤N.A≥0为控制加权因 入了Diophantine方程，并采用递推算法求解. 子.y(k+)是柔化后的设定值序列，满足： 由于CARIMA模型比较接近实际对象特性，且 rya(k)=y(k), 具有积分作用，因此它不仅能为自校正鲁棒控制器 ya(k+j)=aya(k+j-1)+(1-a)y,(k). 的设计奠定良好的基础，而且能有效地消除系统的 式中：0<α≤1为柔化因子，y,是当前设定值， 静态偏差。 将预测方程(8)代入式(10)，并优化求解得 用CARIMA模型将系统表示为如下形式： △u(k),由此可得到当前k时刻的控制量： A(:)y(k)=B(z1)u(k-1)+C(z1)(k)/△. u(k)=u(k-1)+△u(k). 式中：y(k)、u(k)、5(k)分别为系统输出、输入及干 依据广义预测控制的求解过程2,41，可以得 扰信号，A(z-1)、B(z-1)、C(z1)分别是n、m和n阶 到预测控制量u(k),u(k)即为翼伞的单侧下偏量， 的z的多项式，△=1-z u(k)的改变，可以使得式(4)中的力F和力矩M发 如果系统时滞大于零，则B(:)多项式开头的一项 生变化，进而使得式(4)中的变量[⊙.o,o.]改 或几项的系数等于零，为了简单起见，令C(z1)=1.x 变，即翼伞的航向产生偏转，从而实现对翼伞的航向 是：变换的逆算子，称为后移时间算子.有： 进行控制

第6期 李永新，等：基于模糊控制与预测控制切换的翼伞系统航迹跟踪控制 .485 3.2模糊控制 每个变量被划分为5个模糊等级，则需要求取 模糊逻辑在人类的思维和语言交流中普遍存 25条控制规则.具体步骤为： 在，经过几十年的发展和研究发现将模糊逻辑应用 1)根据((k-1),.(k-1),在表1中查找 于自动控制领域，能够体现良好的鲁棒性和控制 相应的△妙。. 性能3] 2)令△地。=△地，在表2中根据（中(k-1), 对系统做如图6的划分，横坐标为翼伞的偏航 .(k-1))查得相应的u(k).此时，有3种情况需要 角中、偏航角误差少。、偏航角误差的变换率△妙。以 考虑： 及u(k),为直观起见单位为度().每个变量均划分 ①根据((k-1),中.(k-1)可以得到惟一相 为5个模糊等级.如图6所示，NB为负大 对应u(k),此时，即为控制量； (negative big),NS为负小(negative small),ZE为零 ②根据((k-1),中.(k-1)可以得到多个相 (zero),PS为正小(positive small),PB为正大 对应的u(k),即u(k)不惟一，此时需选取最小的 positive big). u(k)值作为控制量，以减少电机等控制部件的能量 1.0 损耗； NS PB ③根据（山(k-1),中.(k-1)无法找到相对应 0.5 的u(k),此时需取u(k)的最接近解，如果有多个解 与之接近，则按情况②中所述，选取最小值为控 制量； y 依据上述规则，对控制量u(k)建立如表3中的 模糊规则 图6各变量的隶属度函数 表3控制量u(k)的模糊规则 Fig.6 Membership function of variables Table 3 Fuzzy rules of u(k) 建立如表1所示的期望的翼伞动力学规则表， 中(k-1)》 (k-1) 其中，(k-1)为前一时刻航向角值，.(k-1)为前 NB NS ZE PS PB 一时刻航向角跟踪轨迹误差值，△妙。为期望的偏航 NB Ze ZE ZE ZE NB 角误差变化率. NS PS PS ZE E NB ZE PB PS ZE NS NB 表1期望的翼伞系统动力学规则 PS PB ZE ZE NS NS Table 1 Desired dynamic rules of the parafoil system PB PB Ze E Ze ZE 中.(k-1) 山(k-1) 3.3翼伞系统航迹跟踪控制策略 NB NS ZE PS PB 预测控制能够有效地克服系统滞后、可应用于 NB PB PB PB PB NS NS PB PB PS PS NS 开环不稳定非最小相位系统.但预测控制在运算过 ZE PB PS Ze NS NB 程中需要解Diophantine方程、矩阵求逆以及最小二 PS PS NS NS NB NB PB NB NB NB NB 乘法的递推求解，从而使得计算量较大[16] 建立如表2所示的翼伞动力学规则表，其中， 在翼伞航迹追踪控制的过程中，设计控制器采 中.(k-1)为前一时刻航向角跟踪轨迹误差值，△妙。 用模糊控制与预测控制控制两者相互切换.在偏航 为航向角跟踪轨迹误差的变化率， 角误差较大时使用模糊控制，利用模糊控制运算速 表2翼伞系统动力学规则 度快、鲁棒性好的特点，将航迹误差迅速调整至较小 Table 2 Dynamic rules of the parafoil system 的范围.以此减少单纯使用预测作为控制器在跟踪 中.(k-1) (k-1) 过程中的计算量. NB NS ZE PS PB 图7为控制模式切换流程.在翼伞充满后，系统 NB ZE PS PB PB PB 完成初始化，对翼伞航迹开始定位跟踪.判断偏航角 NS NS ZE PS PB PB ZE NB NS ZE PS PB 误差大于设定值后，控制器切换至运算速度较快的 PS NB NB NS ZE PS PB NB NB NB NS ZE 模糊控制器.在偏航角误差相对较小的时候，控制器 根据翼伞系统的动力学模型以及期望的动力学 切换至预测控制，对翼伞航迹进行精确控制，在翼伞 规则表，计算控制量的模糊规则，即 偏航角误差较大的阶段，不必再进行繁杂的计算，从 (k-1)×.(k-1)→u(k). 而节省运算器的运算时间，提高控制效率

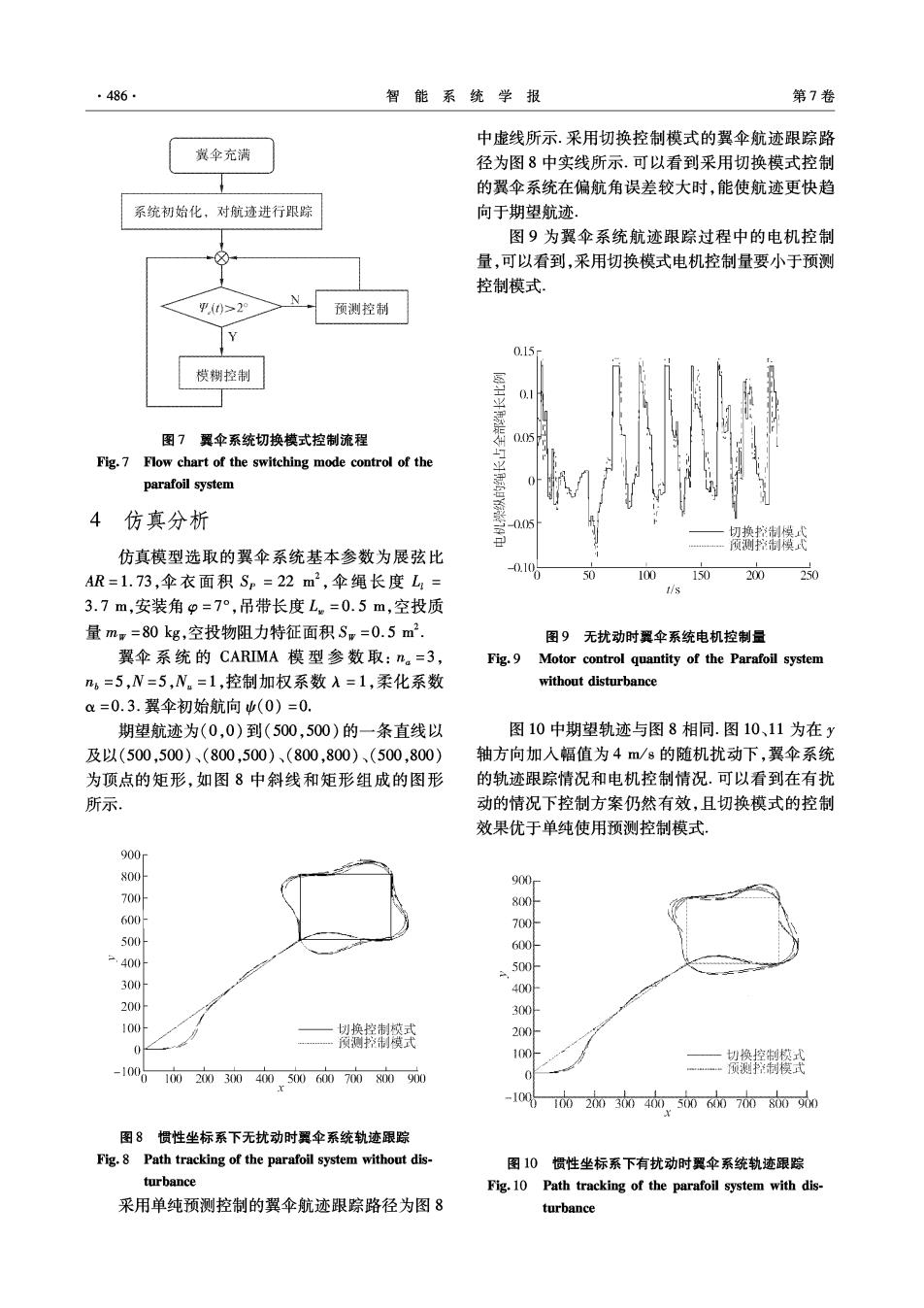
·486 智能系统学报 第7卷 中虚线所示.采用切换控制模式的翼伞航迹跟踪路 翼伞充满 径为图8中实线所示.可以看到采用切换模式控制 的翼伞系统在偏航角误差较大时，能使航迹更快趋 系统初始化，对航迹进行跟踪 向于期望航迹. 图9为翼伞系统航迹跟踪过程中的电机控制 量，可以看到，采用切换模式电机控制量要小于预测 控制模式 N 平(t0>2 预测控制 0.15 模糊控制 图7翼伞系统切换模式控制流程 0.05 Fig.7 Flow chart of the switching mode control of the parafoil system 4仿真分析 风热 仿真模型选取的翼伞系统基本参数为展弦比 -0.10 AR=1.73,伞衣面积Sp=22m2,伞绳长度L= 50 100 150 200 250 t/s 3.7m,安装角p=7°，吊带长度Lw=0.5m,空投质 量mm=80kg,空投物阻力特征面积Sm=0.5m2. 图9无扰动时翼伞系统电机控制量 翼伞系统的CARIMA模型参数取：na=3, Fig.9 Motor control quantity of the Parafoil system n=5,N=5,N.=1,控制加权系数A=1,柔化系数 without disturbance a=0.3.翼伞初始航向(0)=0. 期望航迹为(0,0)到(500,500)的一条直线以 图10中期望轨迹与图8相同.图10、11为在y 及以(500,500)、(800,500)、(800,800)、(500,800) 轴方向加入幅值为4m/s的随机扰动下，翼伞系统 为顶点的矩形，如图8中斜线和矩形组成的图形 的轨迹跟踪情况和电机控制情况.可以看到在有扰 所示。 动的情况下控制方案仍然有效，且切换模式的控制 效果优于单纯使用预测控制模式. 900r 800 900 700 80 600 700叶 500 600 2.400 300 400 200 300 100 投热接餐 200H 0 100 -1006 100200300400.500600700800900 -100 10020300400500600700800g00 图8惯性坐标系下无扰动时翼伞系统轨迹跟踪 Fig.8 Path tracking of the parafoil system without dis- 图10惯性坐标系下有扰动时翼伞系统轨迹跟踪 turbance Fig.10 Path tracking of the parafoil system with dis- 采用单纯预测控制的翼伞航迹跟踪路径为图8 turbance

第6期 李永新，等：基于模糊控制与预测控制切换的翼伞系统航迹跟踪控制 ·487… 0.15 [4]吴兆元.美国X38计划于翼伞返回系统[J】.航天返回 与遥感，2000,21(4)：7-13 WU Zhaoyuan.X-38 CRV and parachute recovery system 005 [J].Spacecraft Recovery Remote Sensing,2000,21 (4):7-13 [5]STEIN J M,MADSEN C M,STRAHAN A L.An overview of the guided parafoil system derived from X-38 experience 投擦接制餐〉 [C]//18th AIAA Aerodynamic Decelerator Systems Tech- 至0.15 nology Conference and Seminar Arlington.Munich,Germa- 50 100 150 200 250 t/s y,2005:516-529. [6]PETRY G,BEHR R.The parafoil technology demonstration 图11 有扰动时翼伞系统电机控制量 project:lessons learned and future visions[C]//14th AIAA Fig.11 Motor control quantity of the parafoil system Aerodynamic Decelerator Systems Technology Conference. with disturbance Munich,Germany,1999:AIAA-99-1755. 5结束语 [7]SOPPA U,STRAUCH H.GNC concept for automated land- ing of a large parafoil[C]//14th Aerodynamic Decelerator 对切换控制摸式下翼伞系统航迹跟踪控制进行 Systems Technology Conference and Seminar.San Francis- 建模和仿真之后，分别比较了无扰动和有扰动情况 c0,USA,1997:AIAA-97-1464. 下，切换模式和单一预测控制方式下翼伞跟踪给定 [8]焦亮.基于翼伞空投机器人系统的自主归航研究[D]. 航迹的情况， 天津：南开大学，2011：3440. 可以看到，在无扰动的情况下，翼伞系统能较好 JIAO Liang.Research on autonomous homing based on 地跟踪给定的轨迹，并且电机的控制量相对于单一 parafoil and air-dropped robot system[D].Tianjin:Nankai University,2011:34-40. 使用预测控制时要小.在增加了随机干扰之后，采用 [9]蒲志刚，李良春，唐波.翼伞系统分段归航方向控制方法 切换模式的翼伞系统仍能对轨迹进行较好地跟踪，电 [J].四川兵工学报，2009,30(10)：117-119. 机控制量也相对要小一些，提高了系统的快速响应，也 PU Zhigang,LI Liangchun,TANG Bo.The direction con- 缩短了调节时间，显示出较好的稳定性和鲁棒性。 trol of the parafoil system's multiphase trajectory[J].Jour- 在偏航角误差较大时，运用模糊控制比使用预 nal of Sichuan Ordnance,2009,30(10):117-119. 测控制更快地趋向于期望轨迹.同时，采用模糊控制 [10]郭叔伟，董杨彪，秦子增.物伞系统动力学模型和讨论 阶段，无需进行Diophantine方程计算、矩阵求逆以 [J].航天返回与遥感，2008,29(3)：3844. 及最小二乘法的递推求解，在一定程度上减少了运 GUO Shuwei,DONG Yangbiao,QIN Zizeng.Dynamic 算器的计算量： model and discussion of the parachute and payload system [J].Spacecraft Recovery Remote Sensing,2008,29 参考文献： (3):3844. [11]KANG Y,HEDRICK J K.Linear tracking for a fixed-wing [1]熊菁.翼伞系统动力学与归航方案研究[D].长沙：国 UAV using nonlinear model predictive control[J].IEEE 防科技大学，2005：1-7. Transactions on Control Systems Technology,2009,17 XIONG Jing.Research on the dynamics and homing project (5):1202-1210. of parafoil system[D].Changsha:National University of [12]CLARKE D W,MOHTADI C,TUFFS P S.Generalized Defense Technology,2005:1-7. predictive control-part I:the basic algorithm[J].Auto- [2]秦子增，葛玉君.可控翼伞飞行转弯控制性能仿真初步 matica,1987,23(2):137-148. 研究[J].宇航学报，1993(1)：89-96. [13]李国勇.智能控制及其Matlab实现[M].2版.北京：电 QIN Zizeng,GE Yujun.Preliminary simulation of flight turn 子工业出版社，2010：163-165,216-219. performance of controllable parafoil systems[J].Joural of [14]王伟.广义预测控制理论及其应用[M].北京：科学出 Astronautics,1993(1):89-96. 版杜，1998：205-233. [3]史献林，余莉.翼伞空中回收系统的研究及其进展[J]. [15]李少远.工业过程系统的预测控制[J].控制工程， 航天返回与遥感，2008,29(1)：1-5 2010,17(4):407415 SHI Xianlin,YU Li.The study and development of the LI Shaoyuan.Model-based predictive control for industrial parafoil mid-air retrieval system[J].Spacecraft Recovery& process-a survey[J].Control Engineering,2010,17(4): Remote Sensing,2008,29(1):1-5. 407415

·488 智能系统学报 第7卷 [16]李桂秋，陈志旺.基于跟踪误差调节的模糊直接广义 陈增强，男，1964年生，教授，博士 预测控制[J].计算机应用研究，2012,27(3)：1009- 生导师，教育部新世纪人才，中国系统 1011,1014 仿真学会理事，中国自动化学会控制理 LI Guiqiu,CHEN Zhiwang.Fuzzy direct generalized pre 论专业委员会委员和过程控制专业委 dictive control based on tracking error adjustment[J].Ap- 员会委员.主要研究方向为智能预测控 plication Research of Computers,2012,27(3):1009- 制、智能优化计算、多智能体系统控制 1011,1014. 等.曾获得省部级科技进步奖4次，发表学术论文150余篇， 作者简介： 被SCI检索100余篇。 李永新，男，1979年生，博士研究 孙青林，男，1963年生，教授，博士 生，主要研究方向为复杂系统建模与控 生导师，中国人工智能学会智能空天专 业委员会委员.主要研究方向为智能预 测控制、嵌入式控制、翼伞自主归航控 制等，发表学术论文60余篇，被SCI、EI 检紫10余篇. 可拓学与创新方法国际研讨会 The International Symposium on Extenics and Innovation Methods 为了交流与总结可拓学30年的研究成果与应用推广经验，以便更好地开展可拓学研究，为国内外从事理论研究和应用研究的专 家、学者和专业技术人员提供一个了解学习可拓学、交流可拓学研究成果的机会，促进和推动各种创新理论与方法的发展，定于2013 年8月16一18日在北京召开“可拓学与创新方法国际研讨会”.会议期间，同时举办“可拓学创立30周年庆典”. 本次会议将为国内外学者提供一个交流最新成果的平台.我们热诚欢迎国内外从事创新研究的高校及科研院所的学者 和企业界代表参加本次研讨会， 会议主题：总结和交流可拓学以及各种创新方法的最新理论和应用研究成果 本次会议欢迎可拓论、可拓工程、可拓创新方法及其它创新理论与方法等领域的论文投稿，主要范围包括（但不限于）： 1)各种创新理论与方法的理论及其应用成果、发明和专利； 2)可拓论：包括可拓集理论、可拓数学、基元理论、可拓逻辑和可拓学的哲学基础及可拓论的应用研究成果； 3)可拓创新方法：包括可拓策略生成方法、转换桥方法、拓展分析方法、共轭分析方法和可拓变换方法等可拓创新方法的 应用研究成果； 4)可拓学与其他学科交叉融合的研究，包括与各专业领域（如信息、设计、机械与电工、自动化、管理与经济等）相结合产 生的可拓工程理论、方法以及它们在各领域的应用研究论文等。 论文发表：所有录用论文将由国际著名的一流科技出版社CRC Press的丛书序列“Communications in Cybernetics,Systems Science and Engineering”出版，并由该出版社提交EI、ISTP及其他科学文库全文检索.部分优秀论文将由会议组委会推荐KY- BERNETES等SC正检索期刊发表.热忱欢迎广大专家、学者、专业技术人员和企业人士踊跃投稿并参加大会. 征文要求：会议语言为汉语和英语.论文必须用英语撰写.所投论文应在国内外未曾公开发表过，在理论、技术、方法或应 用方面有创见的成果.论文须严格按要求撰写（论文模板将在2013年1月前提供，请各位学者关注）.投稿时请同时提交论文 的WORD版本和PDF版本，届时由会议论文集出版商提供模板， 网t址：htp:/web.gdut.edu.cn/~extenics/ISEIM/ISEIMindex.html 重要日期： 论文全文提交截止日期：2013年3月31日 论文录用通知日期：2013年4月30日 最终论文提交：2013年5月10日 会议时间：2013年8月16-18日 联系地址及联系人：(1)广州：东风东路729号中国人工智能学会可拓工程专业委员会办公室（广东工业大学可拓学与创 新方法研究所)（邮编：510090）李剑明老师；(2)北京：海淀区清华东路17号（邮编：100083）中国农业大学理学院陈薇教授 电话：0086-20-37626179传真：0086-20-37626276 电子邮件：extenics(@vip.163.com