
第8卷第6期 智能系统学报 Vol.8 No.6 2013年12月 CAAI Transactions on Intelligent Systems Dee.2013 D0:10.3969/j.issn.1673-4785.201301022 网络出版地址:http://www.cnki.net/kcms/detail/23.1538.TP.20131101.1719.003.html 基于鱼群算法的仿人机器人步态优化 卢嘉敏,杨宜民,付根平 (广东工业大学自动化学院,广东广州510090) 摘要:针对现有步态优化方法中存在的缺点和不足,分析了仿人机器人腿部各关节对步态稳定性的影响,在径向和侧向平 面内以机器人步态的ZMP稳定裕度和整体能耗为参数构造目标函数,利用鱼群算法对基于样条插值方法规划的仿人机器人 步态进行优化.仿真实验表明,该方法不仅能够获得ZMP稳定裕度大、能耗小的仿人机器人平滑步态,而且相对采用遗传算法 对仿人机器人步态优化具有更好的全局搜索能力和更快的寻优速度 关键词:仿人机器人:步态优化:鱼群算法;能耗:ZMP稳定裕度 中图分类号:TP242.6文献标志码:A文章编号:1673-4785(2013)06-0526-06 中文引用格式:卢嘉敏,杨宜民,付根平.基于鱼群算法的仿人机器人步态优化[J].智能系统学报,2013,8(6):526-531, 英文引用格式:LU Jiamin,YANG Yimin,FU Genping.Research on the gait optimization of humanoid robots based on the fish swarm algo- rithm [J].CAAI Transactions on Intelligent Systems,2013,8(6):526-531. Research on the gait optimization of humanoid robots based on the fish swarm algorithm LU Jiamin,YANG Yimin,FU Genping (School of Automation,Guangdong University of Technology,Guangzhou 510090,China) Abstract:This paper focuses on the shortcomings and deficiencies existing in the present gait optimization method. The influence caused by the leg joints of a humanoid robot on the gait stability is analyzed.In the radial and lateral plane,the ZMP stability margin of the gait of a robot and the integral energy consumption are taken as parameters to form a target function,the fish swarm algorithm is applied to optimize the gait of the humanoid robot programmed on the basis of the spline interpolation method.The simulation experiment shows that,by the use of this method,not on- ly may the smooth gait of a humanoid robot with a large ZMP stability margin and small energy consumption be ob- tained,but also the global search capability has been found to be better and the optimization speed is faster,in com- parison to the optimization of the inheritance algorithm used for the gait optimization of a humanoid robot. Keywords:humanoid robot;gait optimization;fish swarm algorithm;energy consumption;ZMP stability margin 双足步行是仿人机器人实现其他功能的前提和 力矩最优的步行和跑步步态.文献[2]不考虑侧向运 基础,是仿人机器人基本的特征和研究的热点.因为 动的影响,通过一种力矩最优的步态优化方法得到 仿人机器人具有结构复杂、高阶数、非线性、强耦合 能量最优的步态.而文献[3]在文献[2]的基础上通 等特点,故采用传统方法难以对其进行良好的控制, 过增加稳定性约束,得到了能耗最小的优化步态,但 所以必须对步态进行优化.文献[1]假设步态的切换 仍在二维平面内研究机器人的步态,不适合仿人机 是瞬时进行的,用被动冲击方程对切换过程进行建 器人在三维空间的步态优化.文献[4]以关节力矩变 模,实现了五连杆无足平面双足机器人的能量最优、 化最小为目标,优化出稳定的步态,但该方法过程较 复杂,只是得到了力矩最小而不是ZMP稳定裕度最 收稿日期:2013-01-14.网络出版日期:2013-11-01. 通信作者:卢嘉敏.E-mail:jia_min_unique2007@163.com 大的步态
第 8 卷第 6 期 智 能 系 统 学 报 Vol.8 №.6 2013 年 12 月 CAAI Transactions on Intelligent Systems Dec. 2013 DOI:10.3969 / j.issn.1673⁃4785.201301022 网络出版地址:http: / / www.cnki.net / kcms/ detail / 23.1538.TP.20131101.1719.003.html 基于鱼群算法的仿人机器人步态优化 卢嘉敏,杨宜民,付根平 (广东工业大学 自动化学院,广东 广州 510090) 摘 要:针对现有步态优化方法中存在的缺点和不足,分析了仿人机器人腿部各关节对步态稳定性的影响,在径向和侧向平 面内以机器人步态的 ZMP 稳定裕度和整体能耗为参数构造目标函数,利用鱼群算法对基于样条插值方法规划的仿人机器人 步态进行优化.仿真实验表明,该方法不仅能够获得 ZMP 稳定裕度大、能耗小的仿人机器人平滑步态,而且相对采用遗传算法 对仿人机器人步态优化具有更好的全局搜索能力和更快的寻优速度. 关键词:仿人机器人;步态优化;鱼群算法;能耗;ZMP 稳定裕度 中图分类号: TP242.6 文献标志码:A 文章编号:1673⁃4785(2013)06⁃0526⁃06 中文引用格式:卢嘉敏,杨宜民,付根平. 基于鱼群算法的仿人机器人步态优化[J]. 智能系统学报, 2013, 8(6): 526⁃531. 英文引用格式:LU Jiamin, YANG Yimin, FU Genping. Research on the gait optimization of humanoid robots based on the fish swarm algo⁃ rithm [J]. CAAI Transactions on Intelligent Systems, 2013, 8(6): 526⁃531. Research on the gait optimization of humanoid robots based on the fish swarm algorithm LU Jiamin, YANG Yimin, FU Genping (School of Automation, Guangdong University of Technology, Guangzhou 510090, China) Abstract:This paper focuses on the shortcomings and deficiencies existing in the present gait optimization method. The influence caused by the leg joints of a humanoid robot on the gait stability is analyzed. In the radial and lateral plane, the ZMP stability margin of the gait of a robot and the integral energy consumption are taken as parameters to form a target function, the fish swarm algorithm is applied to optimize the gait of the humanoid robot programmed on the basis of the spline interpolation method. The simulation experiment shows that, by the use of this method, not on⁃ ly may the smooth gait of a humanoid robot with a large ZMP stability margin and small energy consumption be ob⁃ tained, but also the global search capability has been found to be better and the optimization speed is faster, in com⁃ parison to the optimization of the inheritance algorithm used for the gait optimization of a humanoid robot. Keywords:humanoid robot; gait optimization; fish swarm algorithm; energy consumption; ZMP stability margin 收稿日期:2013⁃01⁃14. 网络出版日期:2013⁃11⁃01. 通信作者:卢嘉敏. E⁃mail:jia_min_unique2007@ 163.com. 双足步行是仿人机器人实现其他功能的前提和 基础,是仿人机器人基本的特征和研究的热点.因为 仿人机器人具有结构复杂、高阶数、非线性、强耦合 等特点,故采用传统方法难以对其进行良好的控制, 所以必须对步态进行优化.文献[1]假设步态的切换 是瞬时进行的,用被动冲击方程对切换过程进行建 模,实现了五连杆无足平面双足机器人的能量最优、 力矩最优的步行和跑步步态.文献[2]不考虑侧向运 动的影响,通过一种力矩最优的步态优化方法得到 能量最优的步态.而文献[3]在文献[2]的基础上通 过增加稳定性约束,得到了能耗最小的优化步态,但 仍在二维平面内研究机器人的步态,不适合仿人机 器人在三维空间的步态优化.文献[4]以关节力矩变 化最小为目标,优化出稳定的步态,但该方法过程较 复杂,只是得到了力矩最小而不是 ZMP 稳定裕度最 大的步态.

第6期 卢嘉敏,等:基于鱼群算法的仿人机器人步态优化 .527· 1步态规划及其稳定性分析 =1 i=1 1.1基于样条插值的步态规划 X ZMP 仿人机器人步态可以分为起步、周期步行和止 喜a低+d (1) 步3个阶段.3个阶段都要满足无奇异位姿、ZMP稳 定性约束、运动协调性和关节角度范围限制等约束 m(+g)y.- n 条件[s),故在起步阶段需先让仿人机器人的膝关 节弯曲再执行起步,起步完成后进入周期步行阶段, 多豆m后+g 在进入止步阶段后需在双足合拢时把双膝伸直,恢 式中:m为连杆i的质量,x、为:、二为连杆i的质心 复仿人机器人起步前的直立状态,以此完成止步.在 位置,g为重力加速度.由于ZMP的x分量和y分量 径向和侧向平面内把仿人机器人简化成图1所示的 类似,为了避免重复,下文只分析ZMP的x分量.把 连杆模型,采用三次样条插值方法[1o规划出步态中 各连杆位姿与关节角度的关系代入式(1)后,得到 的肩关节、踝关节和髋关节的运动轨迹,即9m= 式(2)所示的ZMP的x分量表达式: f(0。,l),xne=fx.,l),x仰=f代d,de,t)和 &ZMIP A/B, yp=f八dn.,d,m,de,t)(其中9nm为手臂的肩关节摆 动角,x。为踝关节的位置,x,和:,为各关键时刻 A=含224amg-4)- i=1k=1j=1 踝关节的位置,xp、yp为髋关节的径向、侧向位 是2acs(g-%)+ 置,d.、d分别为摆动脚落地时和离地时髋关节 到支撑腿踝关节的距离,d、d,m、d分别为摆动 42g,-)(%-9)-42+ j= i=1 脚落地、离地和抬到最高点时髋关节中心在y轴方 i-1 向上的坐标),然后利用几何关系由踝关节和髋关 g.)cos(q;-q:)+losin g; 节的轨迹计算出膝关节的轨迹,最后通过逆运动学 方程求得各关节的角度轨迹. lod qisin q:-d:q:-lo 芝lg cos g+ i-1 gsin-4 dincos+g公ing,小 B=G-】 15 m∑iesg++ sin dgsi (2) 8.9.10 式中:l:、d:分别为连杆i的长度和连杆质心到相应 关节的距离,q:为连杆i与z方向的夹角 由于仿人机器人的质量主要集中在躯干,而髋关 P6. 12.13 节是控制上半身躯干位姿的主要关节,所以髋关节对 ZP轨迹和机器人的步态稳定性的影响很大.踝关节 图1仿人机器人的连杆模型 位姿是规划仿人机器人落脚点、摆动脚高度和调节机 Fig.I Link model of humanoid robot 器人步速的关键关节,摆动脚高度会影响到机器人的 1.2腿部各关节对步态稳定性的影响分析 双脚力矩和能耗,步速的快慢会直接影响到ZMP的 仿人机器人的步态稳定性由ZMP的稳定裕度 变化速率,从而影响机器人的稳定性膝关节是根据 决定.ZMP的稳定裕度是指机器人步行的ZMP值离 踝关节和髋关节轨迹通过几何关系计算出的,故其对 有效稳定区域边缘的最小距离,ZMP的稳定裕度越 步态稳定性的影响没踝关节和髋关节大.图2为根据 大,机器人的稳定性能越好,即ZMP点越接近有效 式(2)计算所得的踝关节、髋关节以及膝关节对仿人 稳定区域中间时机器人的步态越稳定: 机器人步态ZMP的影响图,由图可验证,踝关节和髋 跟据ZMP的计算公式: 关节对ZMP的影响较大,对仿人机器人的ZMP稳定
1 步态规划及其稳定性分析 1.1 基于样条插值的步态规划 仿人机器人步态可以分为起步、周期步行和止 步 3 个阶段.3 个阶段都要满足无奇异位姿、ZMP 稳 定性约束、运动协调性和关节角度范围限制等约束 条件[5⁃9] ,故在起步阶段需先让仿人机器人的膝关 节弯曲再执行起步,起步完成后进入周期步行阶段, 在进入止步阶段后需在双足合拢时把双膝伸直,恢 复仿人机器人起步前的直立状态,以此完成止步.在 径向和侧向平面内把仿人机器人简化成图 1 所示的 连杆模型,采用三次样条插值方法[10] 规划出步态中 的肩关节、踝关节和髋关节的运动轨迹,即 θarm = f(θa,t) , xankle = f(xa,za,t) , xhip = f(dxs,dxe,t) 和 yhip = f(dys,dym ,dye,t) (其中 θarm 为手臂的肩关节摆 动角, xankle 为踝关节的位置, xa 和 za 为各关键时刻 踝关节的位置, xhip 、 yhip 为髋关节的径向、侧向位 置, dxs 、 dxe 分别为摆动脚落地时和离地时髋关节 到支撑腿踝关节的距离, dys 、 dym 、 dye 分别为摆动 脚落地、离地和抬到最高点时髋关节中心在 y 轴方 向上的坐标),然后利用几何关系由踝关节和髋关 节的轨迹计算出膝关节的轨迹,最后通过逆运动学 方程求得各关节的角度轨迹. 图 1 仿人机器人的连杆模型 Fig.1 Link model of humanoid robot 1.2 腿部各关节对步态稳定性的影响分析 仿人机器人的步态稳定性由 ZMP 的稳定裕度 决定.ZMP 的稳定裕度是指机器人步行的 ZMP 值离 有效稳定区域边缘的最小距离,ZMP 的稳定裕度越 大,机器人的稳定性能越好,即 ZMP 点越接近有效 稳定区域中间时机器人的步态越稳定. 跟据 ZMP 的计算公式[11] : xZMP = ∑ n i = 1 mi z ¨ i ( + g) xi - ∑ n i = 1 mi x ¨ i zi ∑ n i = 1 mi(z ¨ i + g) , yZMP = ∑ n i = 1 mi z ¨ i ( + g) yi - ∑ n i = 1 mi y ¨ i zi ∑ n i = 1 mi(z ¨ i + g) . ì î í ï ï ï ï ïï ï ï ï ï ï (1) 式中: mi 为连杆 i 的质量, xi 、 yi 、 zi 为连杆 i 的质心 位置, g 为重力加速度.由于 ZMP 的 x 分量和 y 分量 类似,为了避免重复,下文只分析 ZMP 的 x 分量.把 各连杆位姿与关节角度的关系代入式(1) 后,得到 式(2)所示的 ZMP 的 x 分量表达式: xZMP = A / B, A = ∑ n i = 1 [∑ i-1 k = 1∑ i-1 j = 1 l k l j q · j sin(qj - qk) - ∑ i-1 k = 1∑ i-1 j = 1 l k l j q ¨ j cos(qj - qk) + di∑ i-1 j = 1 l j(q ·2 j - q ·2 i )sin(qj - qi) - di∑ i-1 j = 1 l j(q ¨ j + q ¨ i)cos(qj - qi) + l 0∑ i-1 j = 1 l j q ·2 j sin qj + l 0 di q · 2 i sin qi - d 2 i q ¨ i - l 0∑ i-1 j = 1 l j q ¨ j cos qj + gdi sin qi - l 0 di q ¨ i cos qi + g∑ i-1 j = 1 l j sin qj], B = G - ∑ n i = 1 mi[∑ i-1 j = 1 l j q ·2 j cos qj + di q ·2 j cos qj + ∑ i-1 j = 1 l j q ¨ j sin qj + di q ¨ j sin qj]. (2) 式中: l i 、 di 分别为连杆 i 的长度和连杆质心到相应 关节的距离, qi 为连杆 i 与 z 方向的夹角. 由于仿人机器人的质量主要集中在躯干,而髋关 节是控制上半身躯干位姿的主要关节,所以髋关节对 ZMP 轨迹和机器人的步态稳定性的影响很大.踝关节 位姿是规划仿人机器人落脚点、摆动脚高度和调节机 器人步速的关键关节,摆动脚高度会影响到机器人的 双脚力矩和能耗,步速的快慢会直接影响到 ZMP 的 变化速率,从而影响机器人的稳定性.膝关节是根据 踝关节和髋关节轨迹通过几何关系计算出的,故其对 步态稳定性的影响没踝关节和髋关节大.图 2 为根据 式(2)计算所得的踝关节、髋关节以及膝关节对仿人 机器人步态 ZMP 的影响图,由图可验证,踝关节和髋 关节对 ZMP 的影响较大,对仿人机器人的 ZMP 稳定 第 6 期 卢嘉敏,等:基于鱼群算法的仿人机器人步态优化 ·527·

.528. 智能系统学报 第8卷 裕度有较大影响,其中踝关节和髋关节在起步步行阶 的距离,Visual为人工鱼的感知距离)的伙伴数目 段对仿人机器人步态的稳定性影响最为明显,该影响 n及中心位置X(k)= 随着机器人步态进入周期步行阶段和止步步行阶段 ∑X)n,k=1,2,,n, i= 逐渐减少,而膝关节在步态的起步步行、周期步行和 如果Y/m>8Yy(8为拥挤度),则表明伙伴中心有 止步步行阶段对仿人机器人步态的稳定性影响都较 较多的食物并且不太拥挤,X,应朝伙伴的中心位置 小,可忽略不计,因此,对髋关节和踝关节进行优化可 方向前进一步:否则执行觅食算子 以获得ZMP稳定裕度更大的仿人机器步态, 3)追尾算子, 一髋关节 当人工鱼当前状态为X,,探索当前邻域内 …踝关节 +膝关节 d,8Y:,则表明伙伴X的状态具有较高的食物 0.51.01.52.02.53.03.54.0 浓度并且其周围不太拥挤,则朝伙伴X,的方向前进 t/s 一步,否则执行觅食算子 图2髋、踝和膝关节对机器人步态稳定性的影响 4)行为选择 Fig.2 Influence of hip,ankle and knee joints on 根据所要解决的问题性质,对人工鱼当前所处 robot's gait stability 的环境进行评价,从而选择一种行为.如对于求取极 基于鱼群算法的步态优化设计 大值的问题,最简单的评估方法可以用试探法,就是 模拟执行聚群、追尾等行为,然后评价行动后的值, 鱼群算法是一种基于模拟鱼群行为来寻找全局 选择其中的最大者来实际执行,默认的行为方式为 优化的群智能算法[.该算法对比传统的优化模式 觅食算子 具有分布处理、寻优速度较快、适应能力强的特点, 2.2目标函数的构造 因此,特别适合用于文中具有多约束条件、多参数的 仿人机器人要实现长久稳定的步行,首先要求 步态寻优 其步态具有较大的稳定裕度和较小的能耗,故本文 2.1鱼群算法 以ZMP稳定裕度和整体能耗为参数共同构造目标 鱼群算法中,人工鱼状态表示为向量X,= 函数.假设ZMP稳定裕度的目标函数为J2,整体能 [x4x2…xD],i=1,2,…,N(N为人工鱼群 耗的目标函数为J,则目标函数J=αJ2-BJA(其 个体大小).xD为第i条人工鱼的第D维向量,每条 中α、B∈[0,1],是根据两者对仿人机器人步行 人工鱼状态就是一个潜在的解,将X,带入被优化的 时的比重而设定,由于在J2不变的情况下,能量消 函数,根据函数值的大小衡量X的优劣.人工鱼通 耗越小J越大,故J前为减号). 过随机解进行初始化,然后通过觅食、聚群及追尾等 对于J2,由于仿人机器人步态是由单脚支撑和 算子来更新自己,迭代搜寻最优解,从而实现寻优 双脚支撑交替作用实现的,故要对J2进行分段讨 其中觅食、聚群、追尾算子和行为选择具体如下 论.在步行的单脚支撑期,ZMP必须在支撑脚内才能 1)觅食算子 保证其步态的稳定性.假设在第i个采样时刻,ZMP 当人工鱼当前状态为X:,在其感知范围内随机 到脚内有效稳定区域的x、y方向边界的最小距离 选择一个状态X,如果发现X对应的函数值Y,(目 分别为d,、d,: 标函数)更优,则向该方向前进一步:反之,再重新 f(d,,d,)=ad +bd;. (3) 随机选择状态X,判断是否满足前进条件.这样反 式中:a+b=1,且a/b=L/Wa(La、Wa分别 复尝试try_munber次(觅食行为最大尝试次数)后, 为机器人脚掌的长和宽),则单脚支撑期内ZMP的 如果仍不满足前进条件,则随机移动每步步长。 目标值函数为 2)聚群算子 当人工鱼当前状态为X,探索当前邻域内 Js=∑fd,d,)=a∑+b∑d(4) d=‖lX;-X,‖<Visual(dg为人工鱼个体之间 在双脚支撑期,ZMP的稳定区域为双脚足底所
裕度有较大影响,其中踝关节和髋关节在起步步行阶 段对仿人机器人步态的稳定性影响最为明显,该影响 随着机器人步态进入周期步行阶段和止步步行阶段 逐渐减少,而膝关节在步态的起步步行、周期步行和 止步步行阶段对仿人机器人步态的稳定性影响都较 小,可忽略不计,因此,对髋关节和踝关节进行优化可 以获得 ZMP 稳定裕度更大的仿人机器步态. 图 2 髋、踝和膝关节对机器人步态稳定性的影响 Fig.2 Influence of hip, ankle and knee joints on robot's gait stability 2 基于鱼群算法的步态优化设计 鱼群算法是一种基于模拟鱼群行为来寻找全局 优化的群智能算法[12] .该算法对比传统的优化模式 具有分布处理、寻优速度较快、适应能力强的特点, 因此,特别适合用于文中具有多约束条件、多参数的 步态寻优. 2.1 鱼群算法 鱼群 算 法 中, 人 工 鱼 状 态 表 示 为 向 量 Xi = [xi1 xi2 … xiD ] , i = 1,2,…,N ( N 为人工鱼群 个体大小). xiD 为第 i 条人工鱼的第 D 维向量,每条 人工鱼状态就是一个潜在的解,将 Xi 带入被优化的 函数,根据函数值的大小衡量 Xi 的优劣.人工鱼通 过随机解进行初始化,然后通过觅食、聚群及追尾等 算子来更新自己,迭代搜寻最优解,从而实现寻优. 其中觅食、聚群、追尾算子和行为选择具体如下. 1)觅食算子. 当人工鱼当前状态为 Xi ,在其感知范围内随机 选择一个状态 Xi ,如果发现 Xi 对应的函数值 Yj (目 标函数) 更优,则向该方向前进一步;反之,再重新 随机选择状态 Xi ,判断是否满足前进条件.这样反 复尝试 try_munber 次(觅食行为最大尝试次数)后, 如果仍不满足前进条件,则随机移动每步步长. 2)聚群算子. 当人工鱼当前状态为 Xi , 探索当前邻域内 di,j =‖Xi - Xj‖ < Visual ( di,j 为人工鱼个体之间 的距离, Visual 为人工鱼的感知距离) 的伙伴数目 nf 及中心位置 Xc (k) =∑ m i = 1 Xi (k) / n , k = 1,2,…,n , 如果 Yc / nf > δYi ( δ 为拥挤度),则表明伙伴中心有 较多的食物并且不太拥挤, Xi 应朝伙伴的中心位置 方向前进一步;否则执行觅食算子. 3)追尾算子. 当人工鱼当前状态为 Xi , 探索当前邻域内 di,j < Visual 的伙伴数目 nf ,发现伙伴中 Xi 是伙伴 中最优的(即 Xi 对应的 Yj 为领域内最优解),如果 Yc / nf > δYi ,则表明伙伴 Xi 的状态具有较高的食物 浓度并且其周围不太拥挤,则朝伙伴 Xi 的方向前进 一步,否则执行觅食算子. 4)行为选择 根据所要解决的问题性质,对人工鱼当前所处 的环境进行评价,从而选择一种行为.如对于求取极 大值的问题,最简单的评估方法可以用试探法,就是 模拟执行聚群、追尾等行为,然后评价行动后的值, 选择其中的最大者来实际执行,默认的行为方式为 觅食算子. 2.2 目标函数的构造 仿人机器人要实现长久稳定的步行,首先要求 其步态具有较大的稳定裕度和较小的能耗,故本文 以 ZMP 稳定裕度和整体能耗为参数共同构造目标 函数.假设 ZMP 稳定裕度的目标函数为 JZ ,整体能 耗的目标函数为 JA ,则目标函数 J = αJZ - βJA (其 中 α 、 β ∈ [0,1] ,是根据两者对仿人机器人步行 时的比重而设定,由于在 JZ 不变的情况下,能量消 耗越小 J 越大,故 JA 前为减号). 对于 JZ ,由于仿人机器人步态是由单脚支撑和 双脚支撑交替作用实现的,故要对 JZ 进行分段讨 论.在步行的单脚支撑期,ZMP 必须在支撑脚内才能 保证其步态的稳定性.假设在第 i 个采样时刻,ZMP 到脚内有效稳定区域的 x 、 y 方向边界的最小距离 分别为 dx 、 dy : f dx,dy ( ) = ad 2 x + bd 2 y . (3) 式中: a + b = 1,且 a / b = Lfoot / Wfoot ( Lfoot 、 Wfoot 分别 为机器人脚掌的长和宽),则单脚支撑期内 ZMP 的 目标值函数为 JZS = ∑ n i = 1 f dx,dy ( ) = a∑ n i = 1 d 2 xi + b∑ n i = 1 d 2 yi . (4) 在双脚支撑期,ZMP 的稳定区域为双脚足底所 ·528· 智 能 系 统 学 报 第 8 卷

第6期 卢嘉敏,等:基于鱼群算法的仿人机器人步态优化 .529. 构成的六边形,如图3所示. 式(7)计算出各人工鱼的食物浓度J,取最大者 支撑多边 Jmx,并保存其状态: 有效稳定区域 3)各人工鱼分别执行追尾、聚群和觅食算子, 并分别评价对应的J值,取聚群和追尾算子中的最 ZMP 优J值与Jm比较,如果J优于Jm状态,便取代之; (XZMF-J'2MP)】 4)判断结束条件:根据迭代次数maxgen是否 满足条件,若满足条件则结束迭代,输出最优解,否 则gen自增1,并转3)继续. 图3双足支撑期稳定区域 3仿真实验及结果分析 Fig.3 The diagram of stability region for double phase 本文在MATLAB7.1环境下,以直立状态的仿 设在第j个采样时刻ZMP点到区域边界的最小 人机器人弯膝起步,接着周期步行直至停止步行并 距离为d,,则双脚支撑期内ZP的目标值函数为 恢复身体直立状态的步态仿真,以验证本文利用鱼 Jn=dir 群算法对步态参数优化结果的有效性,同时将基于 (5) 鱼群算法的仿人机器人步态优化(FSASP)与基于遗 而在能耗方面,为保证目标函数值的光滑性,考虑到 传算法的仿人机器人步态优化(GASP)的寻优结果 仿人机器人的能耗主要来源于驱动力的损耗,所以 进行比较,说明本文方法的优越性仿人机器人的结 采用驱动力矩的函数来描述J4,即 构参数如表1所示. 表1仿人机器人各部分参数 r(t)ω,(t),t∈Ts; i=l Table 1 Configuration parameters of humanoid robot (6) ,(r(t)ω,(t)+u(t)d(t)),t∈To 参数 躯干 手臂 大腿 小腿 脚掌 质量/kg 2.1180.368 0.533 0.423 0.158 式中:r为关节驱动力矩,w,为关节角速度,u为双 脚支撑期双脚受到的总力矩,d.为双脚支撑期双脚 长度/m 0.28 0.25 0.14 0.11 0.16 受到的总力矩作用于机器人的力臂长,T、为单脚支 步态规划方法如前文所述,相应参数为:仿人机 撑期,T。为双脚支撑期终上所述,用于优化的最终 器人双臂距离0.20m,两髋关节距离0.10m,脚掌宽 总目标函数为 度0.08m,脚掌高度0.045m,下蹲高度0.03m,抬脚 高度0.01m,步长0.10m,步行周期1.2s,其中单脚 aa+b)-Br)w,(), 支撑期为0.96s,双脚支撑期为0.24s,采样周期为 =1 i=1 0.01s.鱼群算法的相关参数为:V=4,Step=1, t∈Ts; (7) Visual 2,try_munber =50,delta 2,maxgen P2-eg0a0+0d0 100,a=0.8,B=0.2.由于鱼群算法采用随机方式初 始化鱼群,在重复运行30次鱼群算法,求得的参数 t∈To 平均值如下:d=0.041m,de=0.33m,d.= 2.3基于鱼群算法的步态优化流程 0.039m,d,m=0.031m,de=0.009m,把本文优化 根据待优化的步态参数和优化目标,取人工鱼 后的参数值代入步态得到的ZMP轨迹如图4所示, 群个体X=[d.dcd.dmd,e】,以目标函数 三维步态棍状图如图5所示,稳定裕度结果如图6 J计算食物浓度,通过聚群和追尾迭代更新自己,寻 所示,能耗结果如图7所示。 0.10r 找最优解,即ZMP稳定裕度最大及能耗最小的步态 0.06 参数值.采用鱼群算法优化步态参数的流程如下: 0.02 1)初始化各参数值,设定人工鱼群规模N、步 .-0.02 长Step、拥挤度8、最多尝试数ry_munber、delta、 -0.06 最大迭代次数maxgen,并设置迭代次数gen=1; -0.10 00.10.20.30.40.50.60.7 2)在待优化步态参数的取值范围内初始化鱼 x/m 群,随机得到{X,X2,…,Xx},并由其计算出鱼群 图4步态优化后的ZMP轨迹 中各鱼之间的平均距离作为感知距离Visual,根据 Fig.4 The ZMP trajectory after gait optimization
构成的六边形,如图 3 所示. 图 3 双足支撑期稳定区域 Fig.3 The diagram of stability region for double phase 设在第 j 个采样时刻 ZMP 点到区域边界的最小 距离为 ds ,则双脚支撑期内 ZMP 的目标值函数为 JZD = ∑ n j = 1 d 2 sj . (5) 而在能耗方面,为保证目标函数值的光滑性,考虑到 仿人机器人的能耗主要来源于驱动力的损耗,所以 采用驱动力矩的函数来描述 JA ,即 JA = ∑ n i = 1 τ(t)ωτ(t),t ∈ TS; ∑ n i = 1 (τ(t)ωτ(t) + u(t)du(t)),t ∈ TD . ì î í ï ï ï ï (6) 式中: τ 为关节驱动力矩, ωτ 为关节角速度, u 为双 脚支撑期双脚受到的总力矩, du 为双脚支撑期双脚 受到的总力矩作用于机器人的力臂长, TS 为单脚支 撑期, TD 为双脚支撑期.终上所述,用于优化的最终 总目标函数为 J = α(a∑ n i = 1 d 2 xi + b∑ n i = 1 d 2 yi) - β∑ n i = 1 τ(t)ωτ(t), t ∈ TS; α∑ n j = 1 d 2 sj - β∑ n j = 1 τ(t)ωτ(t) + u(t)du(t)), t ∈ TD . ì î í ï ï ï ï ï ï ï ï (7) 2.3 基于鱼群算法的步态优化流程 根据待优化的步态参数和优化目标,取人工鱼 群个体 Xi = [dxs dxe dys dym dye ] , 以目标函数 J 计算食物浓度,通过聚群和追尾迭代更新自己,寻 找最优解,即 ZMP 稳定裕度最大及能耗最小的步态 参数值.采用鱼群算法优化步态参数的流程如下: 1)初始化各参数值,设定人工鱼群规模 N 、步 长 Step、拥挤度 δ 、最多尝试数 try_munber 、 delta 、 最大迭代次数 maxgen ,并设置迭代次数 gen = 1; 2)在待优化步态参数的取值范围内初始化鱼 群,随机得到 X1 ,X2 ,…,XN { } , 并由其计算出鱼群 中各鱼之间的平均距离作为感知距离 Visual, 根据 式( 7) 计算出各人工鱼的食物浓度 J ,取最大者 Jmax ,并保存其状态; 3)各人工鱼分别执行追尾、聚群和觅食算子, 并分别评价对应的 J 值,取聚群和追尾算子中的最 优 J 值与 Jmax 比较,如果 J 优于 Jmax 状态,便取代之; 4)判断结束条件:根据迭代次数 maxgen 是否 满足条件,若满足条件则结束迭代,输出最优解,否 则 gen 自增 1,并转 3)继续. 3 仿真实验及结果分析 本文在 MATLAB 7.1 环境下,以直立状态的仿 人机器人弯膝起步,接着周期步行直至停止步行并 恢复身体直立状态的步态仿真,以验证本文利用鱼 群算法对步态参数优化结果的有效性,同时将基于 鱼群算法的仿人机器人步态优化(FSASP)与基于遗 传算法的仿人机器人步态优化(GASP)的寻优结果 进行比较,说明本文方法的优越性.仿人机器人的结 构参数如表 1 所示. 表 1 仿人机器人各部分参数 Table 1 Configuration parameters of humanoid robot 参数 躯干 手臂 大腿 小腿 脚掌 质量/ kg 2.118 0.368 0.533 0.423 0.158 长度/ m 0.28 0.25 0.14 0.11 0.16 步态规划方法如前文所述,相应参数为:仿人机 器人双臂距离 0.20 m,两髋关节距离 0.10 m,脚掌宽 度 0.08 m,脚掌高度 0.045 m,下蹲高度 0.03 m,抬脚 高度 0.01 m,步长 0.10 m,步行周期 1.2 s,其中单脚 支撑期为 0.96 s,双脚支撑期为 0.24 s,采样周期为 0.01 s.鱼群算法的相关参数为: N = 4, Step = 1, Visual = 2, try_munber = 50, delta = 2, maxgen = 100, α = 0.8, β = 0.2.由于鱼群算法采用随机方式初 始化鱼群,在重复运行 30 次鱼群算法,求得的参数 平均值如下: dxs = 0.041 m , dxe = 0.33 m , dys = 0.039 m , dym = 0.031 m , dye = 0.009 m, 把本文优化 后的参数值代入步态得到的 ZMP 轨迹如图 4 所示, 三维步态棍状图如图 5 所示,稳定裕度结果如图 6 所示,能耗结果如图 7 所示. 图 4 步态优化后的 ZMP 轨迹 Fig.4 The ZMP trajectory after gait optimization 第 6 期 卢嘉敏,等:基于鱼群算法的仿人机器人步态优化 ·529·
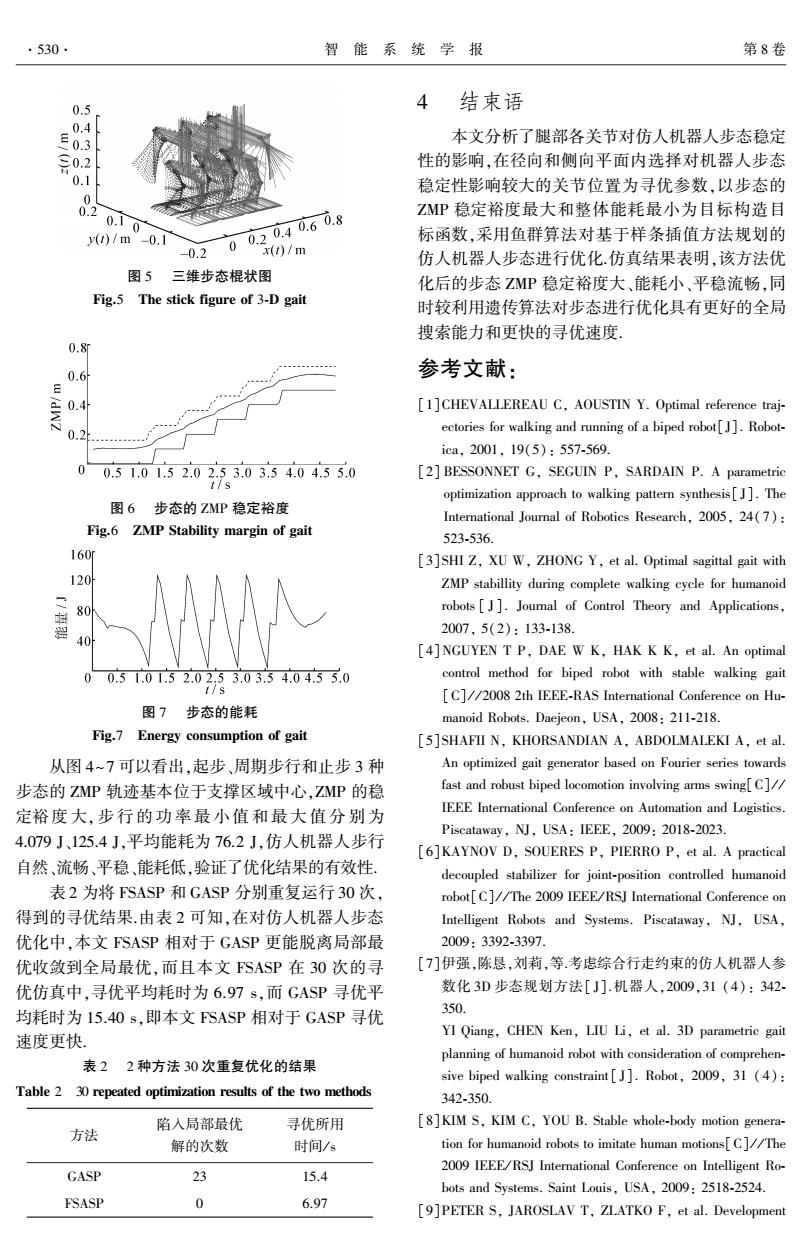
530. 智能系统学报 第8卷 0.5 4 结束语 .0.4 0.3 本文分析了腿部各关节对仿人机器人步态稳定 0.2 性的影响,在径向和侧向平面内选择对机器人步态 0.1 稳定性影响较大的关节位置为寻优参数,以步态的 0 . ZMP稳定裕度最大和整体能耗最小为目标构造目 0.1 0 y(t)/m -01 标函数,采用鱼群算法对基于样条插值方法规划的 -0.2 00.20.40.608 x(t)/m 仿人机器人步态进行优化仿真结果表明,该方法优 图5 三维步态棍状图 化后的步态ZMP稳定裕度大、能耗小、平稳流畅,同 Fig.5 The stick figure of 3-D gait 时较利用遗传算法对步态进行优化具有更好的全局 搜索能力和更快的寻优速度, 0.8 0.6 参考文献: E [1]CHEVALLEREAU C,AOUSTIN Y.Optimal reference traj- ectories for walking and running of a biped robot[J].Robot- 0. ica,2001,19(5):557-569. 00.51.01.52.02.53.03.54.04.55.0 [2]BESSONNET G,SEGUIN P,SARDAIN P.A parametric 1/9 optimization approach to walking pattern synthesis[J].The 图6步态的ZMP稳定裕度 International Journal of Robotics Research,2005,24(7): Fig.6 ZMP Stability margin of gait 523-536. 160 [3]SHI Z,XU W,ZHONG Y,et al.Optimal sagittal gait with 120 ZMP stabillity during complete walking cycle for humanoid 80 robots[J].Joumal of Control Theory and Applications, 2007,5(2):133-138. 40 [4]NGUYEN T P,DAE W K,HAK KK,et al.An optimal 00.51.01.52.02.53.03.54.04.55.0 control method for biped robot with stable walking gait t/s [C]//2008 2th IEEE-RAS International Conference on Hu- 图7步态的能耗 manoid Robots.Daejeon,USA,2008:211-218. Fig.7 Energy consumption of gait [5]SHAFII N,KHORSANDIAN A,ABDOLMALEKI A,et al. 从图4~7可以看出,起步、周期步行和止步3种 An optimized gait generator based on Fourier series towards 步态的ZP轨迹基本位于支撑区域中心,ZMP的稳 fast and robust biped locomotion involving arms swing[C]// 定裕度大,步行的功率最小值和最大值分别为 IEEE International Conference on Automation and Logistics. 4.079J、125.4J平均能耗为76.2J,仿人机器人步行 Piscataway,NJ,USA:IEEE,2009:2018-2023. [6]KAYNOV D,SOUERES P,PIERRO P,et al.A practical 自然、流畅、平稳、能耗低,验证了优化结果的有效性 decoupled stabilizer for joint-position controlled humanoid 表2为将FSASP和GASP分别重复运行30次, robot[C]//The 2009 IEEE/RSJ International Conference on 得到的寻优结果由表2可知,在对仿人机器人步态 Intelligent Robots and Systems.Piscataway,NJ,USA, 优化中,本文FSASP相对于GASP更能脱离局部最 2009:3392-3397. 优收敛到全局最优,而且本文FSASP在30次的寻 [7]伊强,陈恳,刘莉,等.考虑综合行走约束的仿人机器人参 优仿真中,寻优平均耗时为6.97s,而GASP寻优平 数化3D步态规划方法[J].机器人,2009,31(4):342- 均耗时为15.40s,即本文FSASP相对于GASP寻优 350 速度更快。 YI Qiang,CHEN Ken,LIU Li,et al.3D parametric gait planning of humanoid robot with consideration of comprehen- 表22种方法30次重复优化的结果 sive biped walking constraint[J].Robot,2009,31 (4): Table 2 30 repeated optimization results of the two methods 342.350. 陷入局部最优 寻优所用 [8]KIM S,KIM C,YOU B.Stable whole-body motion genera- 方法 解的次数 时间/s tion for humanoid robots to imitate human motions[C//The 2009 IEEE/RSJ International Conference on Intelligent Ro- GASP 23 15.4 bots and Systems.Saint Louis,USA,2009:2518-2524. FSASP 0 6.97 [9]PETER S,JAROSLAV T,ZLATKO F,et al.Development
图 5 三维步态棍状图 Fig.5 The stick figure of 3⁃D gait 图 6 步态的 ZMP 稳定裕度 Fig.6 ZMP Stability margin of gait 图 7 步态的能耗 Fig.7 Energy consumption of gait 从图 4~7 可以看出,起步、周期步行和止步 3 种 步态的 ZMP 轨迹基本位于支撑区域中心,ZMP 的稳 定裕 度 大,步 行 的 功 率 最 小 值 和 最 大 值 分 别 为 4.079 J、125.4 J,平均能耗为 76.2 J,仿人机器人步行 自然、流畅、平稳、能耗低,验证了优化结果的有效性. 表 2 为将 FSASP 和 GASP 分别重复运行 30 次, 得到的寻优结果.由表 2 可知,在对仿人机器人步态 优化中,本文 FSASP 相对于 GASP 更能脱离局部最 优收敛到全局最优,而且本文 FSASP 在 30 次的寻 优仿真中,寻优平均耗时为 6.97 s,而 GASP 寻优平 均耗时为 15.40 s,即本文 FSASP 相对于 GASP 寻优 速度更快. 表 2 2 种方法 30 次重复优化的结果 Table 2 30 repeated optimization results of the two methods 方法 陷入局部最优 解的次数 寻优所用 时间/ s GASP 23 15.4 FSASP 0 6.97 4 结束语 本文分析了腿部各关节对仿人机器人步态稳定 性的影响,在径向和侧向平面内选择对机器人步态 稳定性影响较大的关节位置为寻优参数,以步态的 ZMP 稳定裕度最大和整体能耗最小为目标构造目 标函数,采用鱼群算法对基于样条插值方法规划的 仿人机器人步态进行优化.仿真结果表明,该方法优 化后的步态 ZMP 稳定裕度大、能耗小、平稳流畅,同 时较利用遗传算法对步态进行优化具有更好的全局 搜索能力和更快的寻优速度. 参考文献: [1]CHEVALLEREAU C, AOUSTIN Y. Optimal reference traj⁃ ectories for walking and running of a biped robot[J]. Robot⁃ ica, 2001, 19(5): 557⁃569. [2] BESSONNET G, SEGUIN P, SARDAIN P. A parametric optimization approach to walking pattern synthesis[ J]. The International Journal of Robotics Research, 2005, 24(7): 523⁃536. [3]SHI Z, XU W, ZHONG Y, et al. Optimal sagittal gait with ZMP stabillity during complete walking cycle for humanoid robots [ J ]. Journal of Control Theory and Applications, 2007, 5(2): 133⁃138. [4]NGUYEN T P, DAE W K, HAK K K, et al. An optimal control method for biped robot with stable walking gait [C] / / 2008 2th IEEE⁃RAS International Conference on Hu⁃ manoid Robots. Daejeon, USA, 2008: 211⁃218. [5]SHAFII N, KHORSANDIAN A, ABDOLMALEKI A, et al. An optimized gait generator based on Fourier series towards fast and robust biped locomotion involving arms swing[C] / / IEEE International Conference on Automation and Logistics. Piscataway, NJ, USA: IEEE, 2009: 2018⁃2023. [6]KAYNOV D, SOUERES P, PIERRO P, et al. A practical decoupled stabilizer for joint⁃position controlled humanoid robot[C] / / The 2009 IEEE/ RSJ International Conference on Intelligent Robots and Systems. Piscataway, NJ, USA, 2009: 3392⁃3397. [7]伊强,陈恳,刘莉,等.考虑综合行走约束的仿人机器人参 数化 3D 步态规划方法[ J].机器人,2009,31 ( 4): 342⁃ 350. YI Qiang, CHEN Ken, LIU Li, et al. 3D parametric gait planning of humanoid robot with consideration of comprehen⁃ sive biped walking constraint[ J]. Robot, 2009, 31 ( 4): 342⁃350. [8]KIM S, KIM C, YOU B. Stable whole⁃body motion genera⁃ tion for humanoid robots to imitate human motions[C] / / The 2009 IEEE/ RSJ International Conference on Intelligent Ro⁃ bots and Systems. Saint Louis, USA, 2009: 2518⁃2524. [9]PETER S, JAROSLAV T, ZLATKO F, et al. Development ·530· 智 能 系 统 学 报 第 8 卷

第6期 卢嘉敏,等:基于鱼群算法的仿人机器人步态优化 ·531· of cognitive capabilities for robot Nao in center for intelligent 作者简介: technologies in Kosice C//2011 2nd International Confer- 卢嘉敏,女,1987年生,硕士研究 ence on Cognitive Info-communications.Piscataway,NJ, 生.主要研究方向为机器人技术、智能 USA,2011:1-5. 控制 [10]HUANG Qiang,YOKOI K,KAJITA S,et al.Planning walking patterns for a biped robot[.IEEE Transactions on Robotics and Automation,2001,3(17):280-289. [11]棍田秀司.仿人机器人[M].北京:清华大学出版社, 2007:87-91. 杨宜民,男,1945年生,教授,博士 [12]JIANG Mingyan,WANG Yong.Spread spectrum code esti- 生导师.主要研究方向为机器视觉,多 mation by artificial fish swarm algorithm[C]//IEEE Inter. 机器人技术,人工智能等.发表学术论 national Symposium on Intelligent Signal Processing, 文300余篇,出版著作6部,获国家专 2007,2007:1-6. 利6项. 第5届中国数据挖掘会议 The 5th China Conference on Date Mining(CCDM2014) 数据挖掘与知识发现是是人工智能、机器学习、数据库、统计、模式识别等多个交叉学科的热点研究领 域,其研究成果已应用到多个研究领域,包括机器学习、模式识别、数据库、统计、知识获取、数据可视化、生物 信息学等.中国数据挖掘会议(CCDM,China Conference Data Mining)由中国计算机学会和中国人工智能学会 联合主办、中国计算机学会人工智能与模式识别专委会和中国人工智能学会机器学习专业委员会协办,现已 成为国内数据挖掘、人工智能最主要的学术活动.前4届中国数据挖掘学术会议分别在北京、郑州、烟台和广 州成功举办,为学术和工业界的广大研究人员提供一个交流、合作平台,使得研究人员之间分享数据挖掘与 知识发现领域的创新思想、研究成果、最新研究进展以及系统开发经验.第五届中国数据挖掘会议 (CCDM2014)将于2014年5月24日至26日在浙江省金华市举行,由浙江师范大学数理与信息工程学院 浙江省计算机科学与技术学科联合承办.本次会议将为人工智能、数据挖掘、智能信息处理等相关领域的研 究学者和工程实践人员,开展广泛的学术交流、交流最新研究成果、研讨发展战略,并且将邀请国内机器学习 领域的著名学者做精彩报告,共同促进我国人工智能和数据挖掘理论与技术的发展和应用. 论文出版:会议录用论文将被推荐到《软件学报》、《模式识别与人工智能》、《计算机科学与探索》、《计 算机科学》、《南京大学学报》(自然科学版)、《山东大学学报》(工学版)、《智能系统学报》、《数据采集与处 理》等期刊的正刊发表, 重要日期: 论文提交截止日期:2013年12月31日: 论文录用通知日期:2014年3月31日: 终稿提交截止日期:2014年4月10日: 提前注册截止日期:2014年4月15日: 会议日期:2014年5月24-26日. 联系方式: 通信地址:中国浙江省金华市迎宾大道688号浙江师范大学数理与信息工程学院 邮编:321004 邮箱:ccdm2014@gmail..com,备用邮箱:hwliu(@zjnu.edu.cn(请尽量以E-mail方式联系我们,我们会及 时处理您的邮件!) 电话:0579-82298188 联系人:刘华文(15067999773),胡哲峰(15906898616)
of cognitive capabilities for robot Nao in center for intelligent technologies in Kosice[C] / / 2011 2nd International Confer⁃ ence on Cognitive Info⁃communications. Piscataway, NJ, USA, 2011: 1⁃5. [10] HUANG Qiang, YOKOI K, KAJITA S, et al. Planning walking patterns for a biped robot[ J]. IEEE Transactions on Robotics and Automation, 2001, 3(17): 280⁃289. [11]棍田秀司. 仿人机器人[ M]. 北京:清华大学出版社, 2007: 87⁃91. [12]JIANG Mingyan, WANG Yong. Spread spectrum code esti⁃ mation by artificial fish swarm algorithm[C] / / IEEE Inter⁃ national Symposium on Intelligent Signal Processing, 2007, 2007: 1⁃6. 作者简介: 卢嘉敏,女,1987 年生,硕士研究 生.主要研究方向为机器人技术、智能 控制. 杨宜民,男,1945 年生,教授,博士 生导师.主要研究方向为机器视觉,多 机器人技术,人工智能等.发表学术论 文 300 余篇,出版著作 6 部,获国家专 利 6 项. 第 5 届中国数据挖掘会议 The 5th China Conference on Date Mining(CCDM2014) 数据挖掘与知识发现是是人工智能、机器学习、数据库、统计、模式识别等多个交叉学科的热点研究领 域,其研究成果已应用到多个研究领域,包括机器学习、模式识别、数据库、统计、知识获取、数据可视化、生物 信息学等.中国数据挖掘会议(CCDM,China Conference Data Mining)由中国计算机学会和中国人工智能学会 联合主办、中国计算机学会人工智能与模式识别专委会和中国人工智能学会机器学习专业委员会协办,现已 成为国内数据挖掘、人工智能最主要的学术活动.前 4 届中国数据挖掘学术会议分别在北京、郑州、烟台和广 州成功举办,为学术和工业界的广大研究人员提供一个交流、合作平台,使得研究人员之间分享数据挖掘与 知识发现领域的创新思想、 研究成果、 最新研究进展以及系统开发经验. 第五届中国数据挖掘会议 (CCDM2014)将于 2014 年 5 月 24 日至 26 日在浙江省金华市举行,由浙江师范大学数理与信息工程学院、 浙江省计算机科学与技术学科联合承办.本次会议将为人工智能、数据挖掘、智能信息处理等相关领域的研 究学者和工程实践人员,开展广泛的学术交流、交流最新研究成果、研讨发展战略,并且将邀请国内机器学习 领域的著名学者做精彩报告,共同促进我国人工智能和数据挖掘理论与技术的发展和应用. 论文出版:会议录用论文将被推荐到《软件学报》、《模式识别与人工智能》、《计算机科学与探索》、《计 算机科学》、《南京大学学报》(自然科学版)、《山东大学学报》 (工学版)、《智能系统学报》、《数据采集与处 理》等期刊的正刊发表. 重要日期: 论文提交截止日期:2013 年 12 月 31 日; 论文录用通知日期:2014 年 3 月 31 日; 终稿提交截止日期:2014 年 4 月 10 日; 提前注册截止日期:2014 年 4 月 15 日; 会议日期:2014 年 5 月 24 -26 日. 联系方式: 通信地址:中国浙江省金华市迎宾大道 688 号浙江师范大学数理与信息工程学院 邮 编:321004 邮 箱:ccdm2014@ gmail.com,备用邮箱:hwliu@ zjnu.edu.cn(请尽量以 E⁃mail 方式联系我们,我们会及 时处理您的邮件!) 电 话:0579⁃82298188 联 系 人: 刘华文(15067999773),胡哲峰(15906898616) 第 6 期 卢嘉敏,等:基于鱼群算法的仿人机器人步态优化 ·531·