
第8卷第1期 智能系统学报 Vol.8 No.1 2013年2月 CAAI Transactions on Intelligent Systems Feh.2013 D0I:10.3969/j.issn.1673-4785.201208035 网络出版地址:http://ww.cnki.net/kems/detail/23.1538.TP.20130125.1440.004.html 组合分布估计和差分进化的多目标优化算法 陶新民,徐鹏,刘福荣2,张冬雪 (1.哈尔滨工程大学信息与通信工程学院,黑龙江哈尔滨150001;2.黑龙江省电力有限公司科信处,黑龙江哈尔 滨150090) 摘要:为了提高多目标优化算法的收敛能力及求解精度,提出了一种组合分布估计和差分进化的多目标优化算 法.该方法用分布估计算法和差分进化算法共同生成种群中的粒子,利用选择因子来控制每个粒子的产生方式,并 且根据迭代次数的增加来改变2种算法的使用比例,搜索初期利用分布估计算法进行快速定位,然后用差分进化算 法进行精确搜索,并对差分进化算法的变异因子进行了改进,定义了一个可变的变异因子,来控制不同搜索时期中 差分进化算法的变异范围.用4个测试函数对算法进行了仿真测试,并同NSGA-Ⅱ和RM-MEDA进行了比较.实验结 果表明,该算法具有良好的收敛性和分布性,并且效果稳定. 关键词:多目标优化;分布估计算法;差分进化算法 中图分类号:TP18文献标志码:A文章编号:16734785(2013)01-0039-07 Multi-objective optimization algorithm composed of estimation of distribution and differential evolution TAO Xinmin',XU Peng',LIU Furong2,ZHANG Dongxue (1.College of Information and Communication Engineering,Harbin Engineering University,Harbin 150001,China;2.Science and Information Department,Heilongjiang Electric Power Company Limited,Harbin 150090,China) Abstract:In order to improve the ability of convergence and accuracy of a multi-objective optimization algorithm,a multi-objective optimization algorithm composed of estimation of distribution and differential evolution has been pro- posed.Both estimation of distribution algorithm and differential evolution algorithm will be used to generate parti- cles of population.The generation method of each particle has been decided by using a selective factor,and propor- tion of the use of two algorithms according to the frequency of iterations.Utilizing an estimation of distribution algo- rithm to quickly locate in the initial search,and then differential evolution algorithm was used for accurately con- ducting searches.The variation factor of differential evolution algorithm was improved,and a variable variation fac- tor also was defined and used to control the range of variation of differential evolution algorithm in different search periods.Four test functions were used to evaluate the performance of the proposed algorithm,and next the proposed algorithm was compared with nondominated sorting genetic algorithm II(NSGA-II)and regularity model-based mul- tiobjective estimation of distribution algorithm(RM-MEDA).The experimental results show that the proposed algo- rithm displayed a good convergence,diversity performance,and the stable effects. Keywords:multi-objective optimization;estimation of distribution algorithm;differential evolution algorithm 分布估计算法(estimation of distribution algo-rithm,EDA)是一类新的基于群体搜索的进化算法, 最初在1996年被提出,在2000年前后迅速发展,成 收稿日期:201208-27.网络出版日期:201301-25. 为当前进化计算领域的研究热点).分布估计算法 基金项目:国家自然科学基金资助项目(61074076);中国博土后科学 与传统进化算法不同,算法中没有交叉和变异操作, 基金资助项目(20090450119):中国博士点新教师基金资 助项目(20092304120017). 取而代之的是建立解空间的概率模型,直接描述整 通信作者:徐鹏.E-mail:newadress@126.com

·40 智能系统学报 第8卷 个群体的进化趋势,然后由概率模型采样生成新的 2 群体.文献[24]首先利用EDA求解多目标优化问 组合多目标优化算法 题.2008年,Zhang等提出了基于规则模型的分布估 本文定义了一个选择因子,通过选择因子来控 计多目标算法(regularity model--based multiobjective 制每个新粒子的生成方式,选择用分布估计算法或 estimation of distribution algorithm,RM-MEDA), 差分进化算法生成新粒子,并以概率的方式控制2 法很好地利用了Pareto最优解集的规律性,与基于 种算法在每一次迭代中的使用比例,使得比例随着 父代中心重组的非劣排序遗传算法(parent--centric 搜索时期进行变化,以适应不同搜索时期的搜索需 recombination-based nondominated sorting genetic al- 求.采用从整个群体中选优的种群更新策略,来更好 gorithmⅡ,PCX-NSGA-Ⅱ)及第3代通用差异演化 地符合多目标优化的Pareto最优解的特性, (the third evolution step of generalized differential 2.1分布估计算法 evolution,GDE3)相比,其在多样性上显示了卓越的 分布估计算法首先要建立概率模型,来描述求 性能51。 得的解在空间的分布,然后对概率模型进行随机采 分布估计算法具有良好的全局搜索能力,但局 样,产生新的种群山.本文算法采用固定高度的直 部优化能力较差,对于高维的优化问题常常陷入局 方图(marginal fixed--height histogram,FHH)概率模 部最优解,出现早熟收敛的现象6.差分进化(df 型31,设决策空间的维数为几,固定高度的直方图 ferential evolution,DE)算法是由Stom等[7)于l997 概率模型即是将决策变量第)=1,2,…,n)维的搜 年提出的,文献[8-10]将其应用于多目标优化问题 索空间[4,b]分为若于个子区间,并使每一个子区 的求解.差分进化算法具有高效性、鲁棒性好、易于 间内包含的粒子在第j维分量的个数相同. 与其他算法混合等特点.因此本文将分布估计算 本文算法根据种群中的非劣解来建立分布模 法与差分进化算法相结合,来求解多目标优化问题. 型,因为多目标优化中每一次迭代求得的非劣解数 在求解时,每一次迭代中都同时使用这2种算法来 量不同,如果令子区间包含的样本个数大于1,会产 产生新粒子,并根据搜索时期的不同,对2种算法的 生分配不均匀的现象,所以令每一个子区间包含的 样本数为1,即区间高度为1,这样每一维划分出的 使用比例进行调节,充分发挥了分布估计算法的全 局搜索能力,并且利用差分进化算法来弥补分布估 子区间数都等于算法求得的非劣解的数量 计算法局部优化能力差的不足,以便求得更好的优 设非劣解的个数为P,则建立模型的具体方法 化结果 为:对非劣解第G=1,2,…,n)维的分量进行由小 到大的排序,然后令每个子区间包含1个分量,划分 1多目标优化问题的数学描述 出卫个子区间,相邻分量的中点作为相应子区间的 多目标优化问题是普遍存在的一类问题21,以 边界,搜索空间的边界4、b分别作为第1个子区间 的左边界和最后一个子区间的右边界,这样就建立 最小化为例,无约束多目标优化问题可表示为 了一个由p×n个区间组成的分布模型.生成新粒子 min F(x)=[fi(x)f (x)..f (x)] 的操作方法为:对第G=1,2,…,n)维,在搜索空间 式中:m为目标函数个数,x=[1x2…x.]∈ 第j维划分出的子区间中随机选1个子区间,每个 D为决策向量,D表示决策向量所在的决策空间. 子区间的选择概率都为1/P,在这个区间中随机生 对决策空间D中的任意2个决策向量x1和x2, 成1个值,作为新粒子在第j维的分量,这样就得到 如果满足条件: 1个新的粒子. Hie{1,2,…,m}f(x)≤f(2); 排序后相邻分量间的距离越小,相应区间宽度 3je1,2,…,m(x)<f(2) 就越小,则在这个区间产生的值越密集,故在该区间 则称x1支配x2,记为x1<x2, 范围的解的密度和精度都得到了提高.这样对于非 对决策空间D中的任意一个决策向量x,如果 劣解分布越密集的区域搜索强度就越大,使得算法 满足条件: 可以快速定位到最优解所在的区域.但是在进化后 3x*∈D,x◆<x 期,非劣解数量增多,而本文使用的模型每一维划分 则称x为非劣解或Pareto最优解,D中的Pareto最 的子区间数等于非劣解数量,这样划分出的区间数 优解构成的集合Z称为非劣解集或Pareto最优解 就会增多,在生成新粒子的时候有些区间可能不被 集,相应的集合f(Z)称为Pareto最优前端. 使用到,导致生成粒子不能准确反映出非劣解的分

第1期 陶新民,等:组合分布估计和差分进化的多目标优化算法 41· 布情况 选择因子℃,随着进化代数的增加而逐渐变小, 2.2选择因子 使得α:也随着进化代数的增加而变小,这样差分进 令t为当前迭代次数,则选择因子c,的计算公 化算法在初期的变异范围相对较大,能够辅助分布 式为 估计算法进行全局搜索,而在进化后期,差分进化算 t 法的变异因子比较小,可以在非劣解的分布区域内 (1)》 进行精确的搜索,提高算法的求解精度, 式中:co为常数,t为最大迭代次数.设种群中的粒 2.4种群更新策略 子个数为q,第t-1代种群中的第i(i=1,2,…,q) 多目标优化需要求得的是多个非劣解,往往不 个粒子为x,则在生成第i个新粒子的时候,首先 能单独比较新粒子和原粒子的优劣性,所以本文选 产生一个[0,1]内的随机数P:,如果P:小于c,则用 用从群体中选优的方法选择个体进入下一代5).设 分布估计方法产生一个新粒子;否则,用差分进化算 第t-1代的种群为P-,通过P-生成的新粒子 法对x1进行交叉、变异生成一个新粒子. ,,…,x,组成的种群为P',则令Q=P1U 从式(1)中可以看出,选择因子随着进化代数 P',从Q中选出q个粒子形成种群P 的增加而逐渐变小,这使得在寻优过程中,用分布估 设集合S=x1,x2,…,x1s,则定义S中点 计算法生成新粒子的概率逐渐变小,而用差分进化 :(i=1,2,…,1S1)的拥挤距离d(x:,S)为: 算法生成新粒子的概率逐渐变大,可以实现在寻优 19 初期,主要利用分布估计算法进行搜索,快速地找到 d(,S)=∑1/d(x,), 非劣解的分布区域,而在寻优后期,主要用差分进化 算法进行精确搜索.另外,由于种群中粒子的数量比 dr(,)=(((f(:)-f(x))2+(f(x)- 较多,按概率选择每个新粒子的生成方式,可以使2 f(x)2+…+(f(x)-f()2)n.(5) 种算法在每一次迭代中的使用比例都很好地符合统 式中:m为目标函数的个数, 计规律,使得算法能抵抗随机性的影响,寻优结果更 选择粒子的具体步骤为: 稳定 1)用NSGA-Ⅱ的非劣排序方法[4将集合Q划 2.3差分进化算法 分为F1,F2,…,F,g为划分出集合的数量; 差分进化算法通过类似于遗传算法的变异、交 2)令k=0,P=0; 叉等操作来生成新的个体「),其变异是通过扰动参 3)如果1P1q,则执行5),否则计算结束 [0,1]内的随机数s,则交叉操作公式为: 2.5算法的步骤 y= rC可,s<Pe; 本文算法的流程如图1所示,其具体步骤为: (2) 其他. 1)初始化种群,随机产生q个粒子x,x,…,x 式中:P。为交叉概率,是一个常数.通过交叉、变异 作为初始解,放入集合p中,令t=1; 就可得到一个新粒子 2)计算P-1中粒子的目标函数值; 变异因子α决定了粒子变异范围的大小,因此 3)确定P-1中的非劣解集,按2.1中的方法,根 本文定义了一个可变的变异因子,其计算公式为 据非劣解集对搜索空间的每一维进行区间划分,建 0:=C:+0o: (3) 立分布模型: 式中:t为当前迭代次数,c,为第t次迭代中的选择 4)根据式(1)计算选择因子c,根据式(3)计算 因子,α为一个常数.则第i个粒子的扰动参数向量 差分进化算法的变异因子a,令i=1; 的计算公式变为 5)产生一个[0,1]内的随机数P,如果P:小于 C:=x,1+a,(x2-x3: (4) c,则用分布估计方法产生一个粒子作为新粒子

·42 智能系统学报 第8卷 否则,用差分进化算法根据式(4)和式(2)对x-1进 行变异、交叉操作,生成新粒子; 3仿真实验 6)如果i等于q,则令P'={,,…,},执行 为了验证本文算法的有效性,选取文献[15]中 7),否则,令i=i+1,执行5); Zitzler等提出的测试函数ZDT1、ZDT2、ZDT3、ZDT6 7)令Q=PUP',根据2.4中的方法从Q中选出 对算法进行测试,使用文献[14]中的收敛性指标y和 q个粒子,记为,x吃,…,令P={,吃,…,}; 多样性指标△对算法求得的非劣解集进行评价,并将 8)如果达到最大迭代次数,停止计算,否则,令 本文算法与文献[14]中基于实数编码的非劣排序多目 t=t+1,执行2) 标遗传算法(nondominated sorting genetic algorithmⅡ, NSGA-Ⅱ),文献[5]的RM-MEDA算法进行比较.其中, 初始化种群 NSGA-Ⅱ的实验结果来自文献[14],RM-MEDA和本文 算法的实验结果是用Matlab7.0编程运行获得。 建立分布模型 NSGA-Ⅱ的参数设置为:种群大小为100,进化 代数为250代,交叉概率P。=0.9,n。=20,mm=20, 通过分布估计算法 或差分进化算法生 变异概率pm=1/n,其中n为粒子的维数.RM-ME- 成一个新粒子 DA和本文算法的种群大小为100,进化代数为250 代,RM-MEDA的分类数为5,簇扩展系数是0.25, N 生成了n个新粒子 最大训练次数为50,本文算法中,co=1,P。=0.3, =0.2.本文算法的参数设置是根据其对测试函数 Y 的求解效果选取出来的,具体应用时可以根据实际 更新种群 问题进行调节.RM-MEDA和本文算法都是运行30 次,统计结果的均值和方差.3种算法所得的y的均 满足终止条件 值和方差如表1所示,△的均值和方差如表2所示, RM-MEDA和本文算法运行30次的平均时间如表3 TY 优化结果 所示.图2为RM-MEDA和本文算法某一次运行求 得的4个测试函数的Pareto最优前端.图3为RM 图1本文算法的流程图 MEDA和本文算法在某一次运行中对4个测试函数 Fig.1 Flow chart of the proposed algorithm 所求得的y指标的变化情况. 表1Y的均值和方差 Table 1 The mean and variance of y ZDT1 ZDT2 ZDT3 ZDT6 算法 均值 方差 均值 方差 均值 方差 均值 方差 NSGA-Ⅱ0.03348 0.00475 0.07239 0.03169 0.11450 0.00794 0.29656 0.01314 RM-MEDA 0.030 63 0.00035 0.05672 0.00223 0.07956 0.00116 0.82136 0.00854 本文算法0.001324.0864×10-90.000781.3963×10-90.004814.4532×10-80.009613.5813×10-6 表24的均值和方差 Table 2 The mean and variance of A ZDT1 ZDT2 ZDT3 ZDT6 算法 均值 方差 均值 方差 均值 方差 均值 方差 NSGA-Ⅱ 0.390310.00188 0.43078 0.004720.73854 0.019710.66803 0.00992 RM-MEDA 0.24815 0.00063 0.39492 0.006140.56287 0.000840.73693 0.01157 本文算法 0.15409 0.00013 0.15060 0.00017 0.43107 0.00003 0.57036 0.00174
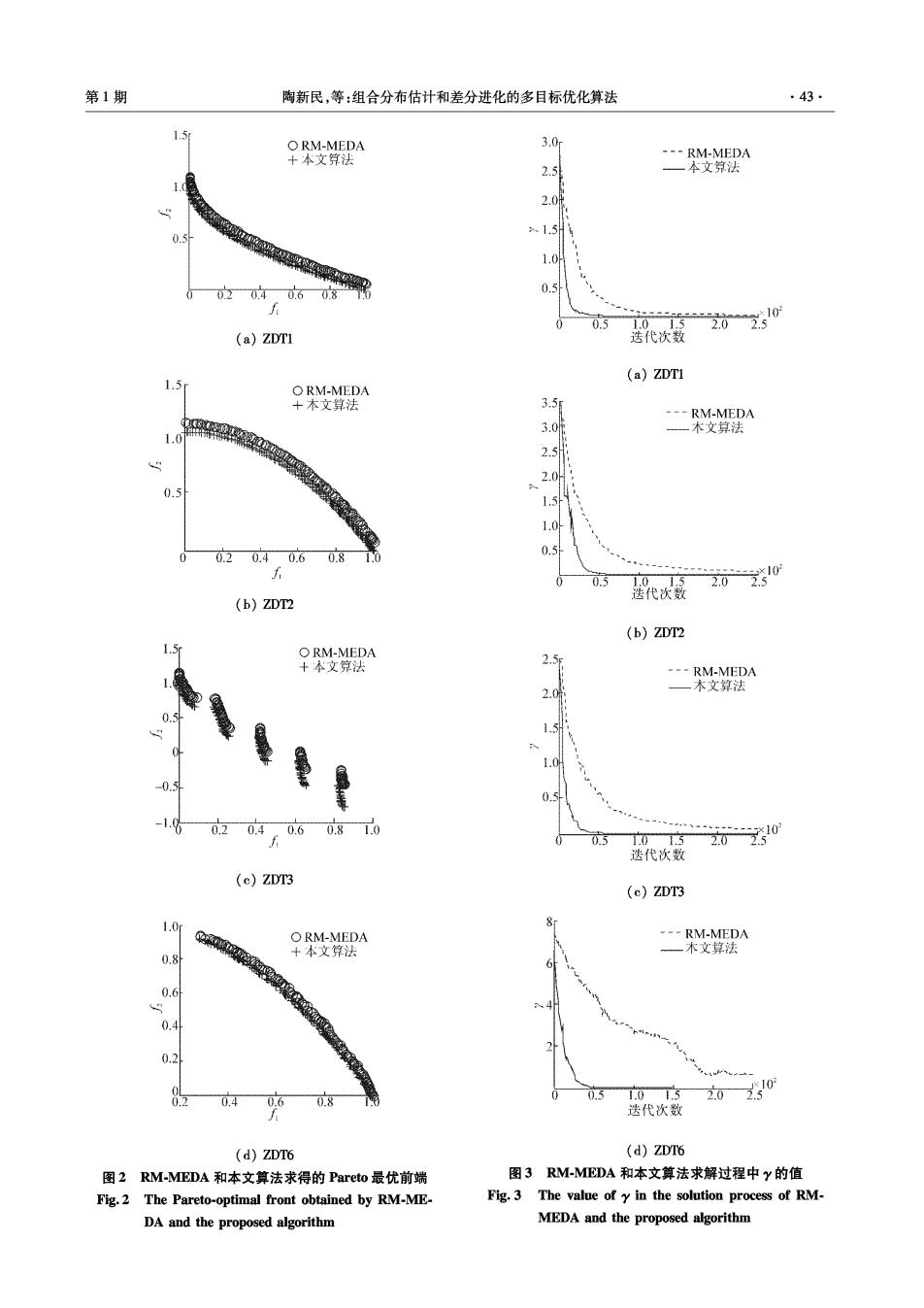
第1期 陶新民,等:组合分布估计和差分进化的多目标优化算法 43· 1.5 ORM-MEDA 3.0m ---RM-MEDA 十本文算 2.5 一本文算法 2.0 1.5 0.5 1.0 020.40.608 77 0.5 f 0.5 1.015 202310 (a)ZDTI 迭代次数 (a)ZDTI 1.5 O RM-MEDA +木文算法 3.5 ---RM-MEDA 3.0 木文算法 1.0 2.0h 0.5 片+5 1.5 1.04 0.2 0.5 0.40.6 0.8 1.0 0.5 法代次 2.0 210 (b)ZDT2 (b)ZDT2 ORM-MEDA 2.5 十本文算法 ---RM-MEDA 2.0 —本文算法 1.0H -0.5 0.5 15 0.20.40.60.81.0 :---×10 0.5 1.01.5 2.0 5 迭代次数 (c)ZDT3 (e)ZDT3 1.0r 8r ORM-MEDA ---RM-MEDA +本文算法 一木文算法 0.8 0.6 4 0.4 0.2 0.2 0.40.60.8 03 T.01.5 2010 迭代次数 (d)ZDT6 (d)ZDT6 图2RM-MEDA和本文算法求得的Pareto最优前端 图3RM-MEDA和本文算法求解过程中y的值 Fig.2 The Pareto-optimal front obtained by RM-ME- Fig.3 The value of y in the solution process of RM- DA and the proposed algorithm MEDA and the proposed algorithm

·44 智能系统学报 第8卷 表3平均运行时间 过分布估计算法使种群快速地收敛,然后利用差分 Table 3 The average running time 进化算法精细搜索的特性来提高求解精度,并在更 算法 ZDTI ZDT2 ZDT3 ZDT6 新种群时进行严密的筛选,以保证新种群的分布性。 RM-MEDA 44.657 8 45.927633.258848.5473 而且该算法根据统计规律来控制每一次迭代中2种 算法的使用比例,使得收敛性和分布性指标的统计 本文算法 8.5531 8.7901 6.6854 9.1746 方差比较小,算法的效果稳定, 从表1可以看出,本文算法对4个测试函数求 得的y的均值和方差都小于前2种算法.对于Pare 4 结束语 to前端为凸的ZDT1函数,3种算法求得的Pareto最 本文提出了一种组合分布估计和差分进化的多 优解集收敛性都比较好,而本文算法求得的Pareto 目标优化算法,根据分布估计算法和差分进化算法 最优解集收敛性好于前2种算法.对于Pareto前端 各自的寻优特性,将2种算法相结合,来弥补各自的 为凹的ZDT2函数,NSGA-I和RM-MEDA求得的 不足.首先充分利用分布估计算法加快了收敛速度, Pareto最优解集的收敛性都有所下降,而本文算法 然后通过差分进化算使得求解精度有所提高,并令 所求得的y的均值和方差与ZDT1函数相比有所减 差分进化算法的变异因子逐渐变化,使得差分进化 小,说明本文算法并没有受到ZDT2函数的凹形Pa- 算法在不同的搜索时期起到不同的作用.通过仿真 reto前端的影响,收敛性更好,更加稳定.对于Pareto 实验,证明了该算法的有效性和稳定性.但固定高度 前端非连续的ZDT3函数,3种算法求得的Pareto最 的分布估计算法只能通过对粒子每一维进行单独建 优解集的收敛性都有所下降,但本文算法好于前2 模来合成整体的模型,这种方法虽然操作简单,却降 种算法.ZDT6的Pareto前端是凹形并且分布不均 低了建模的准确性,如何快速准确地建立模型来提 匀,3种算法求得的y的均值和方差都有所增加,且 高搜索效率是下一步要研究的内容, 本文算法好于前2种算法, 从表2可以看出,本文算法对4个测试函数求 参考文献: 得的△的均值和方差都小于前2种算法.对于ZDT1 [1]周树德,孙增圻.分布估计算法综述[J].自动化学报, 函数,RM-MEDA求得的Pareto最优解集的分布性 2007,33(2):113-124 好于NSGA-Ⅱ,本文算法求得的Pareto最优解集的 ZHOU Shude,SUN Zenggi.A survey on estimation of dis- 分布性优于前2种算法.对于ZDT2函数,RM-ME tribution algorithms[J].Acta Automatica Sinica,2007,33 DA求得的△的均值小于NSGA-Ⅱ,但A的方差大 (2):113-124 于NSGA-Ⅱ,说明RM-MEDA求得的Pareto最优解 [2]KHAN N,GOLDBERG D E,PELIKAN M.Multi-objective 集在分布性上不如NSGA-Ⅱ稳定,而本文算法求得 Bayesian optimization algorithm[R].Urbana,USA:Uni- versity of Illinois at Urbana-Champaign,2002. 的Pareto最优解集的分布性更好,更加稳定.对于 [3]OKABE T,JIN Y,SENDHOFF B,et al.Voronoi-based es- ZDT3函数,本文算法求得的Pareto最优解集的分布 timation of distribution algorithm for multi-objective optimi- 性好于前2种算法,并且分布性更加稳定.对于 zation[C]//Proceedings of the 2004 Congress on Evolution- ZDT6函数,NSGA-Ⅱ求得的Pareto最优解集的分布 ary Computation.Piscataway,USA,2004:1594-1601. 性好于RM-MEDA,本文算法好于前2种算法, [4]SASTRY K,PELIKAN M,GOLDBERG D E.Decompos- 从图3可以看出,本文算法对4个测试函数的 able problems,niching,and scalability of multiobjective es- 求解过程中,Y值在初期的下降速度比RM-MEDA timation of distribution algorithms[R].Urbana,USA:Uni- 快,说明本文算法的收敛速度快于RM-MEDA.可见 versity of Illinois at Urbana-Champaign,2005. 本文算法在初期利用分布估计算法,通过种群中非 [5 ]ZHANG Qingfu,ZHOU Aimin,JIN Yaochu.RM-MEDA:a 劣解的分布情况,快速定位到了最优解区域,并且随 regularity model-based multiobjective estimation of distribu- 着差分进化算法使用比例的逐渐增加,有利于算法 tion algorithm[J].IEEE Transactions on Evolutionary Com- putation,2008,12(1):41-63. 在寻优后期进行精确搜索,从而求得更好的解.从表 [6]程玉虎,王雪松,郝名林.一种多样性保持的分布估计算 3中可以看出,本文算法对4个测试函数运行30次 法[J].电子学报,2010,38(3):591-597 的平均运行时间小于RM-MEDA,说明本文算法的 CHENG Yuhu,WANG Xuesong,HAO Minglin.An estima- 操作和运算相对简单,运行速度快于RM-MEDA. tion of distribution algorithm with diversity preservation[J]. 通过对实验结果的分析可见,本文算法首先通 Acta Electronica Sinica,2010,38(3):591-597

第1期 陶新民,等:组合分布估计和差分进化的多目标优化算法 ·45· [7]STORN R,PRICE K.Differential evolution-a simple and International Conference on Knowledge Based Intelligent efficient adaptive scheme for global optimization over contin- Information Engineering Systems and Allied Technology. uous spaces[J].Joural of Global Optimization,1997,11 Amsterdam,The Netherlands,2001:112-121. (4):341-359. [14]DEB K,PRATAP A,AGARWAL S,et al.A fast and e- [8 ROBIC T,FILIPIC B.DEMO:differential evolution for litist multiobjective genetic algorithm:NSGA-II[J].IEEE multiobjective optimization[C]//Proceedings of the 3rd In- Transactions on Evolutionary Computation,2002,6(2): ternational Conference on Evolutionary Multi-Criterion Opti- 182-197. mization.Berlin,Germany:Springer,2005:520-533. [15 ]ZITZLER E,DEB K,THIELE L.Comparison of multiob- [9]牛大鹏,王福利,何大阔,等.多目标混沌差分进化算法 jective evolutionary algorithms:empirical results[J.Evo- [J].控制与决策,2009,24(3):361-370. lutionary Computation,2000,8(2):173-195. NIU Dapeng,WANG Fuli,HE Dakuo,et al.Chaotic dif- 作者简介: ferential evolution for multiobjective optimization[J].Con- 陶新民,男,1973年生,副教授,硕 trol and Decision,2009,24(3):361-370. 士生导师,博士,主要研究方向为自然 [10 ZHAO Mengling,LIU Ruochen,LI Wenfeng,et al. 计算、数据简约、故障诊断.发表学术论 Multi-objective optimization based differential evolution 文20余篇,其中被I检索8篇, constrained optimization algorithm[C]//Proceedings of 2010 Second WRI Global Congress on Intelligent Sys- tems.Piscataway,USA,2010:320-326. [11]李丽蓉,高卫峰.混合差分进化算法[J小.计算机工程与 徐鹏,男,1987年生,硕士研究生, 设计,2012,33(6):2446-2450. 主要研究方向为自然计算、信号处理. LI Lirong,GAO Weifeng.Hybrid differential evolution al- gorithm[J].Computer Engineering and Design,2012,33 (6):2446-2450. [12]陶新民,刘玉,付丹丹,等.混合变异克隆选择多目标优 化算法[J].计算机仿真,2011,28(10):199-203. TAO Xinmin,LIU Yu,FU Dandan,et al.Hybrid muta- 刘福荣,女,1970年生,副教授,博 tion clonal selection multiobjective optimization algorithm 士,主要研究方向为故障诊断、群智能 [J].Computer Simulation,2011,28(10):199-203. 计算、人工智能. [13]TSUTSUI S,PELIKAN M,GOLDBERG D E.Probabilis- tic model-building genetic algorithms using marginal histo- grams in continuous domain[C]//Proceedings of the 5th