
第7卷第6期 智能系统学报 Vol.7 No.6 2012年12月 CAAI Transactions on Intelligent Systems Dec.2012 D0I:10.3969/i.issn.16734785.201112016 网络出版t地址:htp://www.cnki.net/kcma/detail/23.1538.TP.20120712.1018.002.html 考虑时变时滞的多移动智能体分布式编队控制 雷明,周超,周绍磊,张文广 (海军航空工程学院控制工程系,山东烟台264001) 摘要:考虑到多移动智能体编队控制中的时变时滞问题,在所设计的编队框架下,基于一致性算法设计了具有不 对称时变时滞的分布式编队控制律.该控制律仅使用全局速度导引信息和邻居状态反馈信息;在固定通信拓扑条件 下,推导了具有时变时滞的闭环系统状态方程,应用改进的自由权矩阵方法获得了保守性更小的系统稳定条件,并 在时变通信拓扑条件下,将拓扑变化处理为系统结构的不确定性,同样获得了时变通信拓扑下的系统稳定条件:进 行了6个智能体在平面内编队运动的仿真,实例证明,理论结果是正确的. 关键词:时变时滞;多智能体;编队控制;自由权矩阵;一致性 中图分类号:TP273文献标志码:A文章编号:16734785(2012)06053606 Decentralized formation control of multiple mobile agents considering time-varying delay LEI Ming,ZHOU Chao,ZHOU Shaolei,ZHANG Wenguang (Department of Automatic Control,Navy Aeronautical Engineering Institute,Yantai 264001,China) Abstract:In consideration of the time-varying delay problem in the formation control of multiple mobile agents,we will first examine this area in the study.The defined formation framework,a decentralized formation control law with asymmetric time-varying delay is designed based on a consensus algorithm,which only uses the global velocity guidance and neighbor state feedback information systems.Secondly,under a fixed communication topology condi- tion,the closed-loop system state equation with time-varying delay is induced and a less conservative stability con- dition of the system is obtained using the improved method of free-weight matrix.Further,under the time-varying communication topology condition,stability condition of the system is also obtained by processing topology's varia- tion as a structured model uncertainty.Finally,a simulation example of six agents'formation movement in-plane proves the accuracy of the theory. Keywords:time-varying delay;multiple mobile agents;formation control;free-weight matrix;consensus 以无人机、无人车、无人水下航行器为典型代表为法3]、领航一跟随法46]和基于一致性的方 的移动智能体,能够通过自载的通信设备实时交互 法山虚拟结构法属于集中式控制,控制指令解算 信息、相互协作,实现单一个体无法完成的复杂任 依赖计算中心且随个体数量增多计算量迅速增大; 务,极大地提高了执行任务的可靠性和灵活性.编队 行为法根据预置信息和触发条件形成控制指令,缺 是多移动智能体面临的最基本任务,其目的是使处 乏灵活性和适应性;领航一跟随法过于依赖领航者 于任意初始状态的智能体形成期望的队形并保持队 的状态,一旦领航者故障,编队难以保持;基于一致 形,按照期望的速度运动并能快速变换队形.例如,性的方法属于分布式控制,该方法仅仅需要邻居信 为提高目标搜索效率,多无人机执行宽广区域目标 息,算法简单、计算量小,不受个体数量规模限制,特别 搜索任务时,需要形成特定的编队队形和速度, 是无线自组织网络的迅猛发展,促进了该方法的工程 常见的编队控制方法包括虚拟结构法2]、行 应用研究.文献[7,10-11]基于一致性研究了多智能体 编队控制问题,分别将理论成果应用到多移动机器人、 收稿日期:2011-12-20.网络出版日期:201207-12. 通信作者:雷明.E-mail:Lming999@126.com 多无人机和多智能小车的编队控制中,取得了较好的

第6期 雷明,等:考虑时变时滞的多移动智能体分布式编队控制 ·537 效果,但是均未考虑时滞问题.时滞是造成系统不稳定 过远程网络将编队信息发送给网关智能体,网关智 的一个重要原因,由于通信带宽限制和环境干扰,智能 能体通过局域通信网将编队信息分发到所有智能 体间的通信时滞是不容忽视的,研究具有时滞的多智 体,同时,网关智能体通过局域通信网络汇总所有在 能体一致性编队控制,更加符合实际需要. 网智能体的状态信息,定时上传给控制中心, 时滞一致性算法主要分为2类:一种是对称性 假定智能体具有相同的动态特性,第个智能 算法,即智能体检测自身信息和接收信息都有时滞; 体的动态方程为 另一种是不对称性算法,即仅接收信息有时滞.在实 [x:=, (1) 际系统中,一般只有接收信息有时滞(或检测自身 ly,up 信息的时滞非常小),因此不对称性算法更加贴近 式中:i=1,2,…,N为智能体个数;x:∈R"、:∈R"、 实际.文献[12]研究了具有固定耦合时滞的2种二 4:∈R”分别表示n维欧氏空间中智能体的位置向 阶一致性算法,基于Lyapunov-Krasovskii方法分析 量、速度向量和控制输入向量. 了系统稳定性问题,但是2种二阶一致性算法均属 编队包括编队队形和编队速度2个方面,编队 于对称性算法;文献[13-14]研究了具有固定时滞的 队形是多智能体的空间几何位置关系,编队速度是 二阶平均一致性协议,分别使用频域分析法和LMI 多智能体在空间中的整体运动速度, 的方法获得了保证系统稳定的条件,但是实际中的 定义1在n维欧氏空间中,智能体i期望的空 时滞通常不是固定的;文献[15-16]研究了具有时变 间位置可用向量h:表示,任意2个智能体的相对距 时滯的leader-following一致性协议,使用LMI的方 离向量定义为hg,hg=h:-h,hg在各个坐标轴上的 法获得了系统稳定条件,其编队稳定性与领航者的 投影记为h,k=1,2,…,n,编队向量定义为 状态密切相关,一旦领航者故障,编队难以保持. h=[h:h2…hwhm…hw]T. 本文研究了具有时变时滞的无领航者多智能体编 易证:编队向量与编队队形一一对应,但编队在 队控制问题,提出了多移动智能体的编队控制框架,应 空间中的位置不惟一, 用一致性算法设计了不对称时滞编队控制律,基于自 定义2设定"4为期望的编队速度,当t→∞ 由权矩阵的方法获得了保守性更小的系统稳定条件 时,如果对于Vi,jeN均有x:-=h且v:==。 成立,则称编队形成并保持, 1 多智能体编队框架与预备知识 1.2预备知识 1.1多智能体编队框架 设G=(V,E,A)表示具有n个节点的图,其中 在n维欧氏空间中,每个智能体装配相同的近 V={V,V2,…,Vn}为节点集合,ECV×V为边集 程无线收发设备且具有惟一的标识号,多智能体编 合,A=(ag)为邻接矩阵,如果节点V:和节点V间 队框架如图1所示, 存在信息交互,则a=1,否则,a=0.G的度矩阵D 为对角矩阵,d:= 控制中心 ∑a1:G的拉普拉斯矩阵L- 编队信息 全局状卷信息反馈 D-A,归一化拉普拉斯矩阵L=D-L, 远程通信网络 引理1 Schur补于给定的对称矩阵S=ST= 编队信总 伦局状态信息反馈 r Su 编队信 状态信息反锁 局域 ],其中S和S是方阵,S0使得H+8PP+εQ'Q<0成立. 图1编队框架示意 假定1智能体的通信时滞均相等,时滯和时 Fig.1 Sketch map of formation framework 滞变化率分别为d(t)、d(t)且存在常数d、u,使得 智能体依赖自身通信设备形成局域通信网络, 0≤d(t)≤d,d(t)≤成立. 用于智能体间交互信息;除此之外,网关智能体还具 2 编队控制律设计及稳定性分析 备远程通信能力,用于与控制中心通信.根据任务需 要,控制中心解算出最优的编队队形和编队速度,通 编队控制的目的是使处于任意初始状态的智能

·538 智能系统学报 第7卷 体形成期望的队形和编队速度,因此,编队控制律 rIn☒L1 4:(t)由编队速度控制项4(t)和编队队形控制项 E L☒L2 4(t)2部分组成,其中“g(t)使用全局导引速度信 息和邻居速度反馈信息,其作用是使每个智能体的 1n⑧L 速度均趋近于期望的编队速度;4(t)使用邻居位置反 令(t)=[x(t)v(t)],则闭环系统状态方程 馈信息,其作用是使智能体形成期望的编队队形. 为 u:(t)=ue(t)+ue(t), ui(t)ava-B(vi(t)-v2)- (t)=A5(t)+B(t-d(t))+C. 式中: 最2.a@--” As「0 N 1-(B+1)1 (0=- a0--o》- (2) 式中:"a∈R“、aeR是期望的编队速度和加速度, 0 a是信息权重系数,a、B是控制参数,N:是智能体i C=[a+a,@)+a,@动l 当前时刻的邻居个数。 定理1如果网络拓扑为固定强连通,对于期 将编队控制律写为矩阵形式,则多智能体系统 望的编队向量h、编队速度'a、a和给定的标量d、 的控制律为 u、α、B,若存在正定对称矩阵P、Q、R、Z1、Z2以及任 4。=a(In☒a)+B(Iw☒va)-(B+1)v(t)- 意合适维数的矩阵N1、N2、N3、S、S2、S3、M1、M2、 x(t)+E+(IN-LI)v(t-d(t))+ M3,使得三=宫<0,则编队运动能够形成并保持 (Iw-L☒In)x(t-d(t)), (3) 其中: 重u P2 F3 dN ds, dM dA(Z1+Z2)1 米 中2重23 dN, dS, dM, dB"(Z +Z2) Φ33 dN, ds dM 0 且= dz 0 0 0 dz 0 0 dZ 0 L米常 米 -d(Z1+Z2)J 则 u=PA+A P+Q+R+N+M +N+M, Φ2=-(1-u)2-N2+S2-N+S2, 专()-(A+B)(e)-Bo5(s)ds=0. ④3=-R-M3-S3-Mg-Sg, 对于任意适合维数的矩阵N1、N2N3、S1、S2、S、 中2=p=PB-N1+S1+N+M, M1M2M3,令 电3=p1=-M1-S1+N5+Mg, i(t)=[5(t)5(t-d(t))专(t-d)], Φg=Φ=-M2-S2-Ng+Sg 有 证明如果网络拓扑固定强连通,则工为常值 2gt)W[5e)-5t-d()-o)d]=0, 矩阵,对于期望的编队向量h、编队速度'a和给定 的控制参数aB,E+B(Iw⊙Pa)+ax(Iw⑧Pa)能够惟 2gios6-de)-:-0-”e1-0, 一确定,因此,C为有界常值向量,系统的收敛性与 其自治系统(t)=A转(t)+B形(t-d(t)相同. 2g(t)M[5(t)-5(t-d)-(s)ds]=0. 根据牛顿莱布尼茨公式: 选取Lyapunov--Krasovskii函数 B时(t-d(e))=B5(t)-Bo5o)d, )=5@50+手oZ+Z0+

第6期 雷明,等:考虑时变时滞的多移动智能体分布式编队控制 ·539· o5()05(s)山,+5()R5(s)ds r0182831 0=⊙ 式中:P=p>0,2=Q≥0,R=R≥0,Z1=Z≥0, L**⊙33 Z2=Z≥0.计算V(t)沿着系统的导数 (t)=25(t)P(t)- =PA +AP+2+R N +M +N+M+ (1-d(t)5(t-d())(t-d(t)+ dA (Z +Z)A dNN N+dS ZS +dMZM, (t)(Z+Z2)t)+(e)Q(t)+(t)R5t)- ⊙2=-(1-u)0-N2+S2-N5+dB(Z+Z2)B+ 5(e-d)t-d-[()(Z+z,)o)山≤ dN,NN:+dSZS dM2ZM2, 33 =-R-M3 -S3-M3-S3 dNNN3+ 25(t)P(t)-专(t-d)R传(t-d)+ ds3ZS3 +dMZM3, d传(t)(Z1+Z2)(t)+(t)Q+R)5(t)- 2=PB-N +S2+N+M+dA"(Z -Z)A+ ()(()()) dN NN:+dS ZS+dMZ M:, ez-o2灿+ 03 =-M-S +N M3 dN N'N:+ ds ZS3+dM ZM3, 2giaM5o-u-da)-e]+ =-M2 -S2 -N3 +S3 dN2N N3 dS2ZS3 dMZ M3. 2g0s5-d0)-5:-0-od]+ 如果⊙0,使得三=会<0成立,则编队运动 式中: 能够形成并保持,其中: u23 dN ds, dM dA:(Z +Z2) PD 22市23 dN, ds2 dM, dB.(Z1+Z2) 0 米 3 dN ds dM, 0 0 含= dz 0 0 0 0 米 dz 0 0 0 dZ, 0 0 米 米 -dz2-d(Z1+Z2) d(Z+Z)D 米 -λI ,=中u,市a==中,。=中2+l, 重13=31=中13,3=p2=中3,8=中3 证明如果网络拓扑为动态拓扑,将通信拓扑 0 的变化看做系统的结构不确定性,则闭环系统状态 △B()=-i(®L.-L()⑧L, 方程为 (t)=(A。+△4(t))(t)+ C.=(1.©)+1,©) (B。+△B(t))5(t-r())+C。+△C(t). 式中: ac 时变结构不确定性项△B()用于表示拓扑结构的 变化,易知‖△B(c)I是有界的.令△A(c)=DF()E
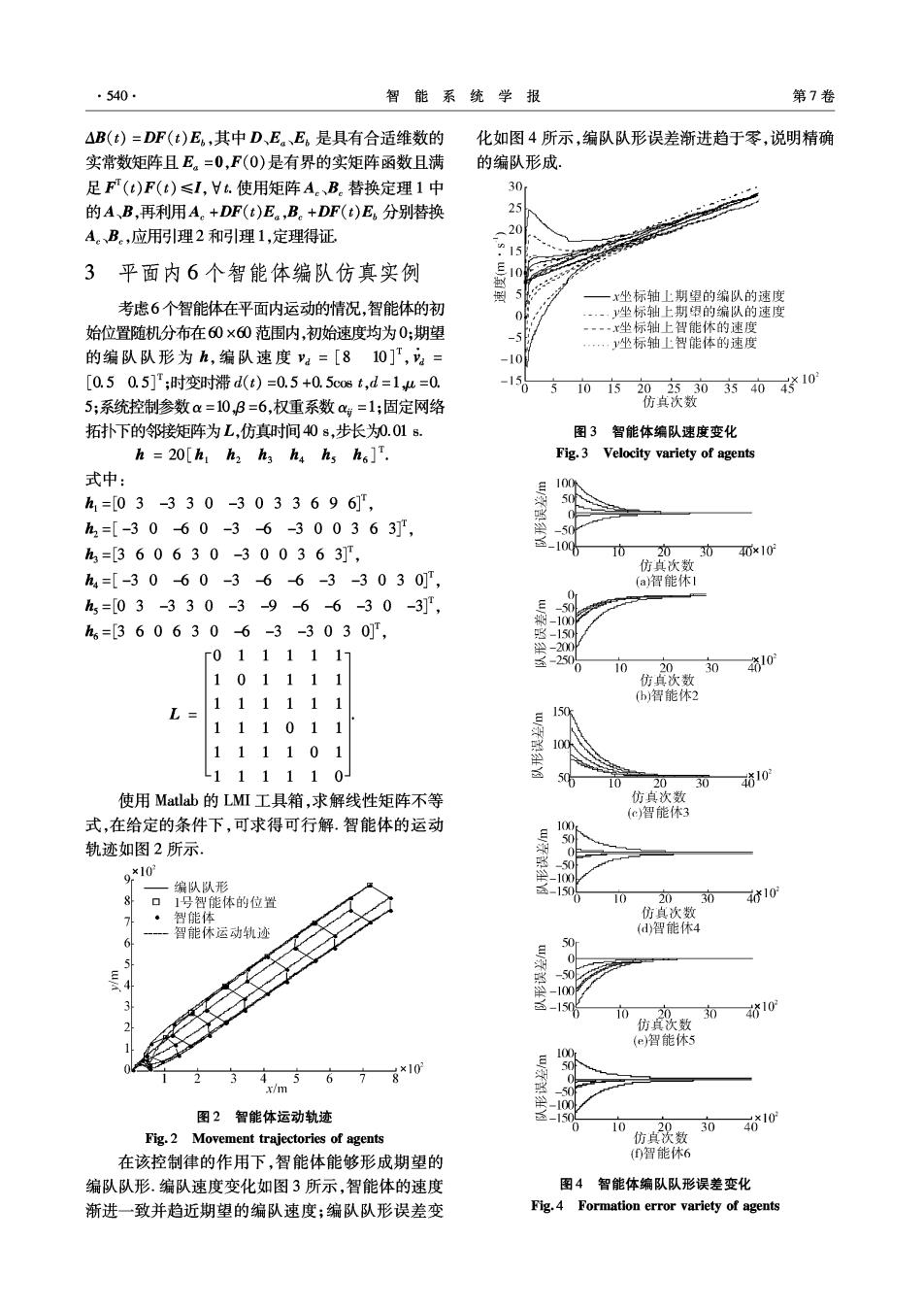
·540 智能系统学报 第7卷 △B(t)=DF(t)E6,其中D、Ea、E。是具有合适维数的 化如图4所示,编队队形误差渐进趋于零,说明精确 实常数矩阵且E。=0,F(0)是有界的实矩阵函数且满 的编队形成。 足FT(t)F(t)≤I,Hk.使用矩阵A。、B。替换定理1中 30 的A、B,再利用A。+DF(t)E。,B。+DF(t)E。分别替换 25 A。B。,应用引理2和引理1,定理得证 、206 h15 3平面内6个智能体编队仿真实例 E x坐标轴上期望的编队的速度 考虑6个智能体在平面内运动的情况,智能体的初 0 …坐标轴上期跟的编队的速度 始位置随机分布在60×60范围内,初始速度均为0;期望 -.-x坐标轴上智能休的速度 坐标轴上智能体的速度 的编队队形为h,编队速度ya=[810]T, -10 [0.50.5];时变时滞d(t)=0.5+0.5c0st,d=14=0. 0 5 0b202克303药40410 5;系统控制参数α=10,B=6,权重系数c=1;固定网络 仿其次数 拓扑下的邻接矩阵为L,仿真时间408,步长为0.018. 图3智能体编队速度变化 h =20[h h2 haha hs ho]". Fig.3 Velocity variety of agents 式中: 100 h=[03-330-3033696], 50i h2=[-3060-36-300363, -50 =[360630-300363], 203040×10 仿真次数 h4=[-3060-366-3-3030], (a)智能休1 =[03-330-3-9-66-30-3], -50 -100 h=[3606306-3-3030], -150 Γ0111117 -200 -250 10 20.304ǒ101 101111 仿真次数 111111 ()智能休2 L 150 111011 1 11101 100 111110 10 20 30 访1o 使用Matlab的LMI工具箱,求解线性矩阵不等 仿真次数 (c)智能体3 式,在给定的条件下,可求得可行解.智能体的运动 100 轨迹如图2所示. 50 9*10 -50 -100 编队队形 益-150 8 1号智能体的位置 10 20 30 410 智能体 仿真次数 智能休运动轨迹 (d智能体4 6 艺 -50 ≥4 -100 3 -1506 10 仿盛数 30 4ǒ10 (e)智能体5 100r 4 5 x/m 678*10 50f -50f 100 图2智能体运动轨迹 10 仿真头数 30 46X10 Fig.2 Movement trajectories of agents 在该控制律的作用下,智能体能够形成期望的 ()智能休6 编队队形.编队速度变化如图3所示,智能体的速度 图4智能体编队队形误差变化 渐进一致并趋近期望的编队速度;编队队形误差变 Fig.4 Formation error variety of agents

第6期 雷明,等:考虑时变时滞的多移动智能体分布式编队控制 ·541· [10 WEI Ren.Leaderless formation control for multiple autono- 4 结束语 mous vehicles C]//AIAA Guidance,Navigation,and 编队控制中,时滞是无法回避的问题.本文以二 Control Conference.Keystone,USA,2006:1-10. 阶智能体为研究对象,考虑到时变时滞的影响,提出 [11]WEI Ren.Distributed coordination architecture for multi- robot formation control[J].Robotics and Autonomous Sys- 了一种分布式编队控制律,并对系统进行了稳定性 tems,2008(56):324-333. 分析,理论推导和仿真结果表明,该控制律能够使处 [12]SU Housheng,ZHANG Wei.Second-order consensus of 于任意初始位置的多智能体形成期望的编队队形, multiple agents with coupling delay[].Communications 在编队机动的过程中保持队形,并能快速进行队形 in Theoretical Physics,2009 (51):101-109 变换, [13]LIU Chenglin,LIU Fei.Consensus problem of coupled dy- namic agents with communication delay[C]//Proceedings 参考文献: of the 29th Chinese Control Conference.Beijing,China, [1]LEWIS M A,TAN K H.High precision formation control of 2010:4501-4505. mobile robots using virtual structures[J].Autonomous Ro- [14]LIN Peng,JIA Yingmin.Consensus of a class of second- bots,1997,4(4):387-403. order multi-agent systems with time-delay and jointly-con- [2]REN W.A decentralized scheme for spacecraft formation nected topologies [J].IEEE Transactions on Automatic flying via the virtual structure approach J].Journal of Control,2010,55(3):778-784. Guidance,Control and Dynamics,2004,27(1):73-82. [15]LIU Chenglin,LIU Fei.Consensus of second-order multi- [3]R.M.Kuppan Chetty,M.Singaperumal,T.Nagarajan.Be- agent systems under communication delay[C]//2010 Chi- havior based multi robot formations with active obstacle avoid- nese Control and Decision Conference.Beijing,China, ance based on switching control strategy[].Journal Advanced 2010:739-744. Materials Research,2012:433-440. [16]ZHU Wei,CHENG Daizhan.Leader-following consensus [4]SHI H,WANG L.Virtual leader approach to coordinated of second-order agents with multiple time-varying delays control of multiple mobile agents with asymmetric interac- [J].Automatica,2010(46):1994-1999. tions[J].Phy8icaD,2006,213(1):51-65. [17]PETERSEN I R,HOLLOT C V.A Riceati equation ap- [5]HU Jiangping,HONG Yiguang.Leader-following coordina- proach to the stabilization of uncertain linear system[J]. tion of multi-agent systems with coupling time delays[J]. Automatica,1986,22(4):397-411 Physica A,2007,374(2):853-863. 作者简介: [6]宗令蓓,谢凡,秦世引.基于MAS的无人机编队飞行智 雷明,男,1983年生,博士研究生, 能优化控制[J].航空学报,2008,29(5):1326-1377. 主要研究方向为无人飞行器编队、多智 GONG Lingbei,XIE Fan,QIN Shiyin.Intelligent optimi- 能体协同控制、无线自组织网络。 zing control of formation flight for UAVs based on MAS[J]. Acta Aeronautica et Astronautica Sinica,2008,29(5): 1326-1377. [7]WEI Ren,ATKINS E.Distributed multi-vehicle coordinated control via local information exchange[J].Int J Robust 周超,男,1982年生,博士研究生, Nonlinear Control,2007,17(10):1002-1033. 主要研究方向为无人飞行器编队协同 [8]吴正平,关治洪,吴先用。基于一致性理论的多机器人系统 控制、预测控制: 队形控制[J].控制与决策,2007,22(11):1241-1244. WU Zhengping,GUAN Zhihong,WU Xianyong.Consensus based formation control of multi-robot system[J].Control and Decision,2007,22(11):1241-1244. [9]吴俊,陆宇平.基于网络通信的多机器人系统的稳定性 周绍磊,男,1963年生,教授,博士 分析[J刃.自动化学报,2010,36(12):1706-1710. 生导师,博土.主要研究方向为先进飞 WU Jun,LU Yuping.Stability analysis of multi-robot sys 行器设计、非线性滤波、自动测试技术、 tem based on network communication[J].Acta Automatica 分布式控制,发表学术论文60余篇,承 Sinica,2010,36(12):1706-1710. 担省部级项目6项,出版专著2部