
第8卷第1期 智能系统学报 Vol.8 No.1 2013年2月 CAAI Transactions on Intelligent Systems Feh.2013 D0I:10.3969/j.issn.1673-4785.201204012 网络出版地址:htp:/nw.cmki.net/kcms/detail/23.1538.TP.20130115.1743.001.html 带执行器饱和的柔性关节机器人位置反馈动态面控制 郭一,刘金琨 (北京航空航天大学自动化科学与电气工程学院,北京100191) 摘要:针对带有执行器饱和的柔性关节机器人系统,提出一种位置反馈动态面控制,以实现机器人连杆的角位置 跟踪.在一般动态面控制的设计框架下,设计观测器重构系统未知速度状态,利用径向基函数神经网络学习饱和非 线性特性,结合“最小参数学习”算法减轻计算负担.通过Lyapunov方法证明得出闭环系统所有信号半全局一致有 界,跟踪误差可以通过调节控制器参数达到任意小.仿真结果表明,控制系统能够克服外界干扰,有效补偿系统存在 的执行器饱和,实现柔性关节机器人的准确跟踪控制.该方法避免了传统反演设计存在的“微分爆炸”现象,简化了 设计过程. 关键词:柔性关节机器人;动态面控制;执行器饱和;神经网络;观测器 中图分类号:TP24文献标志码:A文章编号:16734785(2013)01002107 Position feedback dynamic surface control for flexible-joint robots with actuator saturation GUO Yi,LIU Jinkun (School of Automation Science and Electrical Engineering,Beihang University,Beijing 100191,China) Abstract:The research explored the compensation of flexible-joint robot's actuator saturation using a dynamic sur- face controller for tracking control of link position.Under the design of a general dynamic surface control,an ob- server was designed to aid in the estimation of unknown velocity states.Radical basis function (RBF)neural net- work was used to examine saturation nonlinearity and "minimal learning parameter"technique for the reduction of computational burden.Based on the Lyapunov stability analysis,it was shown that the control strategy could guar- antee the semi-global stability of the closed-loop system and arbitrarily small tracking error by adjusting the control- ler parameters.The simulation results indicated that the proposed control system may overcome the external disturb- ances,compensate for the existing actuator saturation of systems effectively,and realize more accurate tracking con- trol for flexible-joint robots.The proposal eliminates the problem of"explosion of complexity"existing in traditional backstepping approaches and simplifies controller design procedures plainly. Keywords:flexible-joint robots;dynamic surface control;actuator saturation;neural network;observer 随着科技的进步,机器人被广泛应用于机械加 方法遍及反馈线性化法31、奇异摄动法14]、智能控 工、航天、太空探测等多种行业.由于谐波减速器和 制56]、变结构控制等. 关节力矩传感器的使用,实际机器人系统通常带有 实际工程中的机器人系统通常带有不同程度的 关节柔性.研究与实践表明,如果在控制设计时 非匹配不确定性,而反演设计(backstepping)恰恰为 忽略关节柔性,那么机器人执行高频率和高精度任 非匹配不确定非线性系统控制提供了一种有效方 务的能力将会受到很大的限制2.因此,国内外许 法.文献[8-9]用反演控制完成了柔性关节机器人的 多学者对柔性关节机器人的控制方法展开了研究, 连杆位置跟踪.然而,反演控制的设计存在“微分爆 炸”现象,由于需要对非线性函数重复求导,因此复 收稿日期:201204-18.网络出版日期:201301-15. 基金项目:教育部高等学校博士学科点专项科研基金资助项目 杂程度会随着系统阶数的增加而剧增.为了克服这 (20121102110008). 通信作者:郭一,E-mail:guoyiandy@yahoo..cm. 个缺点,Swaroop等o1提出了动态面控制,通过引入

·22 智能系统学报 第8卷 一阶低通滤波器大大简化了设计过程. 小值限制.这说明,假如控制输入超出限制范围,则 本文针对柔性关节机器人系统,考虑两大实际 控制指令不能被执行机构完全执行.将控制输入超 问题:1)执行器饱和,即控制输入受执行器上下界 出执行器范围的部分定义为δ,即 限制;2)位置反馈,即速度信号不可测时仅利用位 置信号设计控制律.采用动态面控制避免反演设计 6=u-u0={0, umin0为高斯基函数的宽度. 业m,l0>认max; 引理1)】对于紧集2CR”上的任意连续函 u=8at(o)= 40, umin0,通过选择合适的中间层 uain,ho≤Umin' 神经元数量N以及合适的参数b和d:(i=1,2,…, 式中:wm>0,umn<0分别是执行器的最大值和最 N),总存在理想权向量0°∈R“使得神经网络

第1期 郭一,等:带执行器饱和的柔性关节机器人位置反馈动态面控制 ·23· 0·(x)可以足够逼近给定函数f,并且逼近误差绝 导,得 对值不大于σM,即 S=2-x1d=2+x2-x1d (5) fx)=0T(x)+o·,x∈2 设计虚拟控制x2: 式中:σ·为逼近误差且满足Iσ·I≤ow: %2=-c1S1+%1 由于0·未知,故需要设计自适应律在线估计. 式中:c1为正数.将2输入到如下时间常数为T2的 仿照文献[14],假设存在已知正数0w使得 低通滤波器,得到新的状态变量x2a: I0*‖≤0w T2x2a+x2u=x2,x2u(0)=x2(0) 2.2观测器设计 2)定义第2个误差表面S2=2-xd,并对其求 由于速度状态不可测,需要设计观测器对状态 导,得 进行重构.设计观测器如式(3): S2=a1x3+fi(x1)+1x2+D2x1-x2d,(6) 九1=入2+1(1-入1)+D(x1-入), 设计虚拟控制3: i2=a3+f(x1)+D2(x1-入), (3) 西=[-()-D,41+4-cS2]. a11 入3=入4+12(x3-入3)+D3(x3-入3), 式中:c2为正数.将x3输人到如下时间常数为T3的 入4=a2u+(1,)+D4(x-3). 低通滤波器,得到新的状态变量x: 式中:l1、l2、D、D2、D3、D4均为待设计的正数,设计 T33u+x3u=x3,3u(0)=x3(0) 方法将在稳定性分析部分给出.利用式(4)重构系 3)定义第3个误差表面S3=:-x3,并对其求 统状态: 导,得 rx1=入1, $3=x4-xu=无4+4-3r (7) 2=2+1(x1-A1), (4) 设计虚拟控制4: 名=入: %4=-C3S3 +%3 金4=九4+4(-3). 式中:c3为正数.将x4输人到如下时间常数为T4的 式中::(i=1,2,3,4)为状态估计值.定义估计误差 低通滤波器,得到新的状态变量x4: x=x-x,由式(3)~(4)得到 T4x4u+x4=x4,x4(0)=x4(0) 名=2+1(x1-入)+D(x1-入)=+D, 4)定义最后一个误差表面S4=x4-xd,并对其 =a+f(x)+D2(x1-入1)+l1(x2-名-D)= 求导,得 a1为+f()+l+(D2-lD), S4=a2u+f(x1,x3)+2x4+D43-x4d= 病=+l2(-)+D(的-3)=店+D5, a24+a26+f(x1,x3)+l2x4+D43-xu.(8) 由于6是连续函数,可以用RBF神经网络逼近 =4山+()+D,(两-)+,(4--D5) 6=0T5(xN)+o a2u+f(x1,x3)+2x4+(D4-2D3)3 式中:|o·1≤oM,‖0°‖≤0M·神经网络补偿器的 记D2=D2-1D1,D4=D4-12D3,则 输入选为xw=[出12西4]T5.定义 在=东+D,, ‖0*‖2=中,中为中的估计值,设计实际的控制器: 2=a13+f(x1)+112+D21, 山=[-6(1,)-D,病+-c4]- d2 名=4+D, 25.455 (9) 4=山+(,)+hd+D,. 式中:c4为正数设计参数估计的自适应律: 2.3控制器设计 针对单连杆柔性关节机器人系统,仿照反演控 市=rS65-nr, 制的“递进式”设计方法,将整个复杂系统分解成4 式中:T、n为正设计参数 个子系统,逐层设计虚拟控制量,并一直后退到整个系 这种控制器设计方法采用了“最小参数学习” 统,进而得到最终的控制量.控制器的设计步骤如下. 算法[16,定义‖0°‖2=中并估计中.如此便无需在 1)定义第1个误差表面S,=x-x,并对其求 线估计每个权值,大大减小了计算量;并且待设计量

·24 智能系统学报 第8卷 T是常数而非矩阵,减轻了调参负担.需要指出的 是,在利用神经网络学习饱和非线性特性时,虽然 0={∑s+行+买+a,r6≤2p1 =2 “最小参数学习”算法的引入减轻了计算负担,但是 式中:P是任意正数.注意到,2×22也是紧集,并 由于自适应律估计的不是权向量,所以无法得到神 且B(i=2,3,4)在2×22上有最大值,记为M.考 经网络学习的动态过程.第3部分将从理论角度论 虑Lyapunov函数: 证神经网络学习结果可以代表饱和非线性特性. V=1+V2+V3+V4 3稳定性分析 式中:=含.=分含=分含, 动态面控制设计过程简单并且具有一定规律 20T-8 性,但是由于低通滤波器的引入,稳定性证明较复 定理1考虑由对象(2)、观测器(3)与实际控 杂文献[10]给出了一般动态面控制的稳定性证明过 制器(9)组成的闭环系统.如果满足假设1并且初 程,在此基础上,给出本文控制系统的稳定性证明。 始条件满足V(0)≤P,其中p是任意正数,则存在可 定义边界层误差: 调参数c(i=1,2,3,4)、T:(i=2,3,4)、1、2、T、7、 y=xa-x4,i=2,3,4. D:(i=1,2,3,4)使得闭环系统所有信号半全局一致 结合低通滤波器表达式得到 有界,系统跟踪误差可以收敛到任意小残集内。 =-年i=2,34 证明首先对V,求导,得 定义=中一中,将设计的虚拟控制和实际控制 V,≤S,(S2+y2+x2-cS1)+S2[a1(S3+y3)+ 1x2-c2S2]+S3(S4+y4+x4-c3S3)+ 代入式(5)~(8)得到: S1=S2+y2+龙+为-xu=S2+2+龙-cS1, S4(-705+a,0*"5+a40+4-6). 2=a(S3+y⅓+为)+f(x1)+l1名+D2x-xu 由于 a1(S3+y3)+1-c2zS2, 2s55+分≥s,05. $=S4+y4++-=S4+y4+-CS3, 1 $=-2,5转若+a,0专+%0+4-c 4sag5+a805≤-7sg5+z 、 对边界层误差求导,得 则 ,≤S(S2+y2+x2-cS)+S2[a(S3+y3)+ 方=-药=-上+c3-u, lx2-c2S2]+S3(S4+y4+4-c3S3) 1 1 为=4-名=-为-1(-方-几,转+4-, 2S85专+20+S,(a0'+4-cS,). T31 (13) 方=4-花=-业+6的-花心 T4 对V2、V3分别求导,得 可知,存在非负连续函数B:(i=2,3,4)使得 6≤(-安+B1, (14) Ti +≤, (10) 3=(x2-2-Dx)+x2(41-12-D2)+ +≤B(S及网⅓4西uu,,(1I)) 3(x4-元4-D33)+x4(△2-l24-D43)= 73 元2-D-l1好-D2+x4-D3号- 9≤ l2-D4x34+△12+△2x4 选取D2=D4=1并利用p/2+安/2≥p:lxI≥△*,得 B4(S1,S2,S3,S4y2y3y4,元,五,4,xu,1d,xd).((12) 由不等式(10)~(12)容易得到如下不等式: ≤-0暖-候-唱-候++ 2+2 城≤-立+B,1yl,i=2,3,4 (15) Ti 对V求导,得 考虑如下紧集: 2:={(xd,xa,xa):xid+d+xid≤X}, 么=abd=7s5-4nd.(16)

第1期 郭一,等:带执行器饱和的柔性关节机器人位置反馈动态面控制 ·25· 综合式(13)~(16),利用Young不等式得到 显然,闭环系统所有信号半全局有界,并且有 ≤2(S+s)+2(S+)+2(S+)+ 恤)≤号 2(S+s)+2(+)+,(+)+ 这意味着可以通过调节参数c:(i=1,2,3,4)、r:(i= 2,3,4)、l1、2、D1、D2、D3、D4、7、使得r任意大,即 (S+s》+(+》+(+》+ 跟踪误差任意小,证明完毕. 稳定性分析中利用李雅普诺夫稳定条件实现观 受+受(+)+(+》-合+ 测器参数设计,并且证明了观测误差可以达到任意 含-号+学+》-5-)-n 小,这说明观测结果能够满足原系统状态的物理意 义.此外,中能够达到任意小,理论上验证了神经网 络学习的有效性, 居-阔-4坛+营鸟,等 4仿真实验与结果 整理得 仿真实验中,理想轨迹设定为xa=sin(t),设定 ≤号-6+++经-6+侵+受- 执行器的最大输出范围为-2~2N·m.假设外部 干扰力矩为△1=0.5sin(2t)和△2=0.4cos(2t).取 系统物理参数:Mgl=5N·m,K=20N·m/ad,I= 信号++受4暖- 4kg·m2,J=1kg·m2,初始状态设为x(0)= [0.100.050].用于估计连续函数8的神经 贼+1-)房+1-2g-2+ 网络采用4-18-1的结构.控制参数选取如下:1= 2=5,D1=D3=4,D2=D4=1,T2=T3=T4=0.01, ++是++ c1=3,c2=8,c3=5,c4=5,n=0.01,T=100. 仿真结果如图3~6.图3反映连杆角位置跟踪效 控制参数选取如下: 果,点线表示理想轨迹,实线表示实际输出.图4反映 11≥2(1+r),l2≥2(1+r),D1≥r,D3≥r, 控制转矩,由于执行器饱和的影响,控制转矩保持在 6≥2+,%≥2+a+ L1 +r, -2~2N·m的范围内.图5和6分别反映了系统2个 速度状态的估计效果,点线表示实际状态,实线表示估 c3≥ ++r≥ 1a22 +2+2+ 计状态.仿真结果说明,在执行器存在饱和的情况下, 连杆角位置也能快速从初始状态跟踪上目标轨迹,克 1 1,M,1 a M 22+2+,≥2+2 +r, 服了饱和非线性特性,神经网络补偿器起到了补偿效 T3 果;估计状态与实际状态几乎重合,观测效果良好,观 ≥分+竖7产2r 测器起到了状态估计作用.总之,所提出的策略保证了 闭环系统半全局稳定,对外界干扰具备一定的鲁棒性 式中:r为待设计正数.则 1.5 -2+0+含袋-) 2 1.0 式中:Q=3/2+(p1+p2)/2+a2(1+σ)/2+ a29/2,选取r≥Q/(2p).由于当V=p时,B:≤M :i 成立,所以当V=p时,V≤-2p+Q≤0.由此可知 V≤P是一个不变集,即如果V(0)≤P,则对所有t>0 0.5 均有V(t)≤p.由于有条件V(0)≤P,所以有 -1.0 V≤-2rV+Q. (17) 12 解式(17),得 t/s v≤是+[vo-是1e 图3跟踪效果 Fig.3 Tracking performance
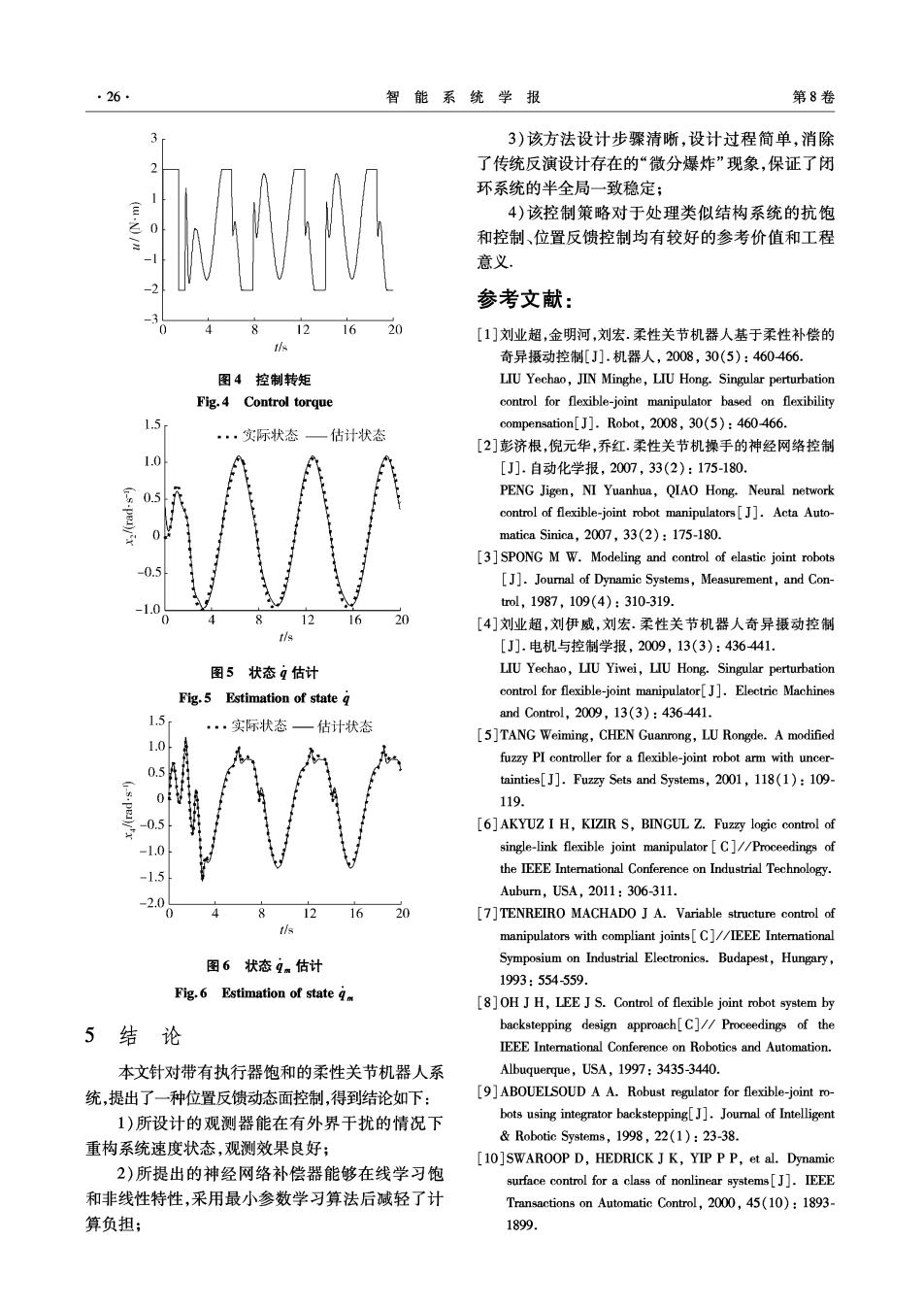
·26 智能系统学报 第8卷 3)该方法设计步骤清晰,设计过程简单,消除 了传统反演设计存在的“微分爆炸”现象,保证了闭 非 环系统的半全局一致稳定; 4)该控制策略对于处理类似结构系统的抗饱 和控制、位置反馈控制均有较好的参考价值和工程 意义 参考文献: 12 16 20 [1]刘业超,金明河,刘宏.柔性关节机器人基于柔性补偿的 tis 奇异摄动控制[J].机器人,2008,30(5):460466. 图4控制转矩 LIU Yechao,JIN Minghe,LIU Hong.Singular perturbation Fig.4 Control torque control for flexible-joint manipulator based on flexibility 1.5 ·实际状态一估计状态 compensation[J].Robot,2008,30(5):460-466. [2]彭济根,倪元华,乔红.柔性关节机操手的神经网络控制 1.0 [J].自动化学报,2007,33(2):175-180. 0.5 PENG Jigen,NI Yuanhua,QIAO Hong.Neural network control of flexible-joint robot manipulators[J].Acta Auto- matica Sinica,2007,33(2):175-180. [3]SPONG M W.Modeling and control of elastic joint robots 0.5 [J].Journal of Dynamic Systems,Measurement,and Con- 1.0 tol,1987,109(4):310-319. 12 16 20 [4]刘业超,刘伊威,刘宏.柔性关节机器人奇异摄动控制 t/s [J].电机与控制学报,2009,13(3):436441. 图5状态g估计 LIU Yechao,LIU Yiwei,LIU Hong.Singular perturbation Fig.5 Estimation of state g control for flexible-joint manipulator[J].Electric Machines 1.5 and Control,2009,13(3):436441. .·实际状态一估计状态 [5]TANG Weiming,CHEN Guanrong,LU Rongde.A modified 1.0 fuzzy PI controller for a flexible-joint robot arm with uncer- 05 tainties[J].Fuzzy Sets and Systems,2001,118(1):109- 119. -0.5 [6]AKYUZ I H,KIZIR S,BINGUL Z.Fuzzy logic control of single-link flexible joint manipulator[C]//Proceedings of the IEEE Interational Conference on Industrial Technology Auburn,USA,2011:306-311. 2.0 16 20 [7]TENREIRO MACHADO J A.Variable structure control of manipulators with compliant joints[C]//IEEE Interational 图6状态9m估计 Symposium on Industrial Electronics.Budapest,Hungary, 1993:554-559. Fig.6 Estimation of state gm [8]OH J H,LEE J S.Control of flexible joint robot system by 5结论 backstepping design approach[C]//Proceedings of the IEEE Interational Conference on Robotics and Automation. 本文针对带有执行器饱和的柔性关节机器人系 Albuquerque,USA,1997:3435-3440. 统,提出了一种位置反馈动态面控制,得到结论如下: [9]ABOUELSOUD AA.Robust regulator for flexible-joint ro- 1)所设计的观测器能在有外界干扰的情况下 bots using integrator backstepping[J].Joumal of Intelligent Robotic Systems,1998,22(1):23-38. 重构系统速度状态,观测效果良好; [10]SWAROOP D,HEDRICK J K,YIP PP,et al.Dynamic 2)所提出的神经网络补偿器能够在线学习饱 surface control for a class of nonlinear systems[J].IEEE 和非线性特性,采用最小参数学习算法后减轻了计 Transactions on Automatic Control,2000,45(10):1893- 算负担; 1899

第1期 郭一,等:带执行器饱和的柔性关节机器人位置反馈动态面控制 ·27 [11]OH J H,LEE J S.Backstepping control design of flexible [16]CHEN Bing,LIU Xiaoping,LIU Kefu,et al.Direct adap- joint manipulator using only position measurements [C] tive fuzzy control of nonlinear strict-feedback systems[J]. Proceedings of the 37th IEEE Conference on Decision and Automatica,2009,45(6):1530-1535 Control.Tampa,USA,1998:931-936. 作者简介: [12]NICOSIA S,TOMEI P.A tracking controller for flexible 郭一,男,1988年生,硕士研究生, joint robots using only link position feedback[J].IEEE 主要研究方向为动态面控制与智能 Transactions on Automatic Control,1995,40(5):885- 控制. 890. [13]PARK I,SANDBERG I W.Universal approximation using radial-basis-function networks J].Neural Computation, 1991,3(2):246-257. [14]WANG Dan.Neural network-based adaptive dynamic sur- 刘金琨,男,1965年生,教授,博士 face control of uncertain nonlinear pure-feedback systems 生导师.主要研究方向为智能控制、机 [J].International Journal of Robust and Nonlinear Con 器人控制和电机控制等.曾主持国家自 tol,2011,21(5):527-541. 然科学基金、航空基金等项目12项.发 [15]GAO W Z,SELMIC RR.Neural network control of a class 表学术论文90余篇,其中被I检索20 of nonlinear systems with actuator saturation[J].IEEE 余篇,出版专著4部. Transactions on Neural Networks,2006,17(1):147-156. 可拓学与创新方法国际研讨会 International Symposium on Extenics and Innovation Methods 为了交流与总结可拓学30年的研究成果与应用推广经验,以便更好地开展可拓学研究,为国内外从事理论 研究和应用研究的专家、学者和专业技术人员提供一个了解学习可拓学、交流可拓学研究成果的机会,促进和推 动各种创新理论与方法的发展,定于2013年8月16一18日在北京召开“可拓学与创新方法国际研讨会”.会议期 间,同时举办“可拓学创立30周年庆典”.本次会议将为国内外学者提供一个交流最新成果的平台.我们热诚欢迎 国内外从事创新研究的高校及科研院所的学者和企业界代表参加本次研讨会· 本次会议欢迎可拓论、可拓工程、可拓创新方法及其他创新理论与方法等领域的论文投稿,主要范围包括(但 不限于): 1)各种创新理论与方法的理论及其应用成果、发明和专利; 2)可拓论:包括可拓集理论、可拓数学、基元理论、可拓逻辑和可拓学的哲学基础及可拓论的应用研究成果; 3)可拓创新方法:包括可拓策略生成方法、转换桥方法、拓展分析方法、共轭分析方法和可拓变换方法等及可 拓创新方法的应用研究成果; 4)可拓学与其他学科交叉融合的研究,包括与各专业领域(如信息、设计、机械与电工、自动化、管理与经济 等)相结合产生的可拓工程理论、方法以及它们在各领域的应用研究论文等 重要日期 论文全文提交截止日期:2013年3月31日 论文录用通知日期:2013年4月30日 最终论文提交:2013年5月10日 会议时间:2013年8月16一18日 联系地址及联系人 (1)广州:番禺区广州大学城外环西路100号中国人工智能学会可拓工程专业委员会办公室(广东工业大学 可拓学与创新方法研究所)(邮编:510006)李剑明老师; (2)北京:海淀区清华东路17号(邮编:100083)中国农业大学理学院陈薇教授. 电话:0086-20-39322973