
第8卷第1期 智能系统学报 Vol.8 No.1 2013年2月 CAAI Transactions on Intelligent Systems Feh.2013 D0I:10.3969/j.issn.1673-4785.201205012 网络出版地址:htp:/nw.cmki.net/kcms/detail/23.1538.TP.20130125.1427.001.html 改进的萤火虫算法求解阻塞流水线调度问题 郭丽萍,李向涛,谷文祥2,殷明浩 (1.东北师范大学计算机科学与信息技术学院,吉林长春130117;2.长春建筑学院基础教学部,吉林长春130607) 摘要:为了提高阻塞流水线调度问题的求解性能,提出了一种改进的萤火虫算法来求解阻塞流水线调度问题。首 先,提出一种离散机制把个体的实数编码形式转换成离散的作业序列,从而使算法能够应用于离散问题求解;其次, 设计一种双重初始化方法,并将NEH启发式方法应用到初始化中来,使算法有一个较优的初始化环境,提高初始种 群的解的质量:此外,重新设计了算法中个体的移动方式来增大搜索域:最后,以一定概率对种群中的个体进行局部 搜索,加强算法的局部搜索性能.通过对Taillard数据集中部分实例进行求解,实验结果验证了新算法的有救性。 关键词:阻塞流水线调度问题;萤火虫算法;离散机制;NEH启发式;局部搜索 中图分类号:TP301.6文献标志码:A文章编号:1673-4785(2013)01003306 An improved firefly algorithm for the blocking flow shop scheduling problem GUO Liping',LI Xiangtao',GU Wenxiang2,YIN Minghao' (1.Department of Computer Science and Information Technology,Northeast Normal University,Changchun 130117,China;2.De- partment of Basic Subjects Teaching,Changchun Architecture Civil Engineering College,Changchun 130607,China) Abstract:In order to improve the solving performance of the blocking flow shop scheduling problem,the researcher proposes to examine an improved firefly algorithm.Firstly,a discrete mechanism was proposed to convert the real coded form of individuals to discrete job sequences,so that the algorithm could be used to deal with discrete prob- lems.Secondly,a double-initialization method was designed and the NEH (Nawaz-Enscore-Ham)heuristic method was applied to the initialization,which provided a superior initial environment and improved the quality of the solu- tion of the initial population.In addition,the research paper focused on redesigning the movement pattern of indi- viduals to enhance the search space.Finally,a local search algorithm was applied to individuals with a certain probability,for the purpose of enhancing the ability to search locally.The improved firefly algorithm was then test- ed utilizing the Taillard datasets,and the results verified the effectiveness of the new algorithm. Keywords:blocking flow shop scheduling problem;firefly algorithm;discrete mechanism;NEH heuristic method; local search 流水线调度问题是一类重要的组合优化问题, hard.该问题的解决方法主要分为构造性启发式 阻塞流水线调度问题作为其中的一个重要分支,由 方法23和元启发式方法4].萤火虫算法8是由剑 于具有很强的工程背景和实际意义,而得到了越来 桥大学的Yang在2008年提出来的一个模拟自然界 越多学者的关注,目前人们已经证明包含2台机器 中萤火虫发光行为的仿生算法,目前该算法在函数 以上的阻塞流水线调度问题的计算复杂性为NP 优化方面表现出较优的性能].为了使萤火虫算法 适用于求解阻塞流水线调度问题,本文对萤火虫算 收稿日期:2012-0507.网络出版日期:201301-25 法进行了一些改进,加强了算法的搜索性能,且避免 基金项目:国家自然科学基金资助项目(60803102,61070084). 通信作者:郭丽萍.E-mail:guolp281@nenu.edu.cm 了萤火虫算法早熟的问题

·34 智能系统学报 第8卷 阻塞流水线调度问题 时间的最小值e3.3为21,对应的作业执行顺序为 1 {J3,J2,J1},如图1所示。 阻塞流水线调度问题可以描述为:n个作业J1, M J2,…,Jn要在m台机器M1,M2,…,Mm上运行,每 M 个作业包含m道工序,每个作业的工序必须按照统 M 一顺序在m台机器上执行,每个作业在每台机器上 的运行时间是固定的,要求协调不同作业的执行顺 4 序,使得某种生产性能指标达到最优.阻塞流水线调 812 162024 度问题的约束条件包括如下: 图1问题的甘特图表示 1)每个作业在每台机器上只能加工1次; Fig.1 The Gantt chart of the example 2)每台机器每次最多只能加工1道工序; 2萤火虫算法 3)每台机器上的作业加工顺序相同; 4)作业的某道工序在某台机器上的加工一旦 萤火虫算法是一种通过模拟自然界中萤火虫发 开始,便不能终止; 光行为的仿生算法.目前,人们对自然界中萤火虫的 5)一个作业完成某道工序后,该作业将在当前 发光行为的意义还存在很多争议,不过有2点是确 机器上滞留直到下游机器变为可用为止。 定的:吸引配偶和吸引潜在的猎物. 在该问题中,用π={π1,π2,…,πn}表示一个 般情况下,可见光的强度随着当前位置到光 调度序列,00=1,2,…,n;k=1,2,…,m)表示作 源距离的增大而减小,另外,空气还要吸收一部分光 业j在机器k上执行一个无间断的工序,其所需时 源.因此,董火虫发出光只在一定的距离范围内可以 间为P.k=1,2,…,n;k=1,2,…,m),e,(=1,2, 被其他萤火虫看见.萤火虫算法约定9):1)萤火虫 …,;k=0,1,…,m)表示第j个作业在第k台机器 之间不存在性别之分,每只萤火虫都可以吸引其他 上的离开时间.则有: 的萤火虫,也可以被其他的萤火虫吸引;2)萤火虫 e1,0=0, (1) 的吸引力和它们发出的光的亮度成正比,因此,对于 e1,k=e1,k-1+p1,k,k=1,2,…,m-1,(2) 任意2只萤火虫来说,亮度较弱的萤火虫会朝着亮 e.0=e-11,j=2,3,…,n, (3) 度较强的萤火虫飞行;如果当前可见光距离范围内, ek=max{,k-1+P.k,e-l,k1},j=2,3,…,n, 没有比自己更亮的萤火虫时,则该萤火虫实行随机 k=1,2,…,m-1, (4) 飞行策略:3)光的亮度一般由求解问题的目标函数 em=e,m-1+Dm,j=1,2,…,n. (5) 决定. 本文选取最大完工时间最小为优化指标,那么 在萤火虫算法中,每只萤火虫称为一个“个 最大完工时间C=(π)=em,m,且它的计算复杂性为 体”,每个个体包含亮度、吸引力、位置等属性.在该 0(mn). 算法中,个体在某个固定位置的亮度I是固定的,该 以3个作业J1、J2、J为例,下面举例说明如何 变量的设定取决于具体问题的目标函数.其他个体 求解阻塞流水线调度问题,3个作业在3台机器上 看到该个体的亮度则随着它们之间距离的增大而减 运行所需时间如表1所示.第1个作业在第1台机 小,此外,传播介质也会吸收一部分光线,因此,个体 器上运行所需要的时间为3,第1个作业在第2台 在距离当前位置「处的亮度还和介质的吸收率有 机器上运行所需要的时间为4,依此类推, 关9].一般把一个个体在距离该个体r处的亮度表 表1时间矩阵 示为 Table 1 Time matrix of an example I(r)=1oer2. (6) 机器 式中:1,为个体在当前所处位置的亮度,y为介质的 作业 M M M 吸收率.有时,为了减小个体亮度变弱的速率,式 (6)也可用如下公式代替: J 3 3 2 6 5 1()=1+7 7 每个个体对其他个体的吸引力B也是相对的, 由式(1)~(5)可以计算出该问题的最大完工 它随着2个个体之间距离的增大而减小;此外,吸引

第1期 郭丽萍,等:改进的萤火虫算法求解阻塞流水线调度问题 ·35 力还和介质的吸收率有关9),因此把个体在距离该 个体的最小完工时间.让2个种群中的个体按序号 个体为r的位置对其他个体的吸引力定义为 两两进行比较:种群1中的第1个个体和种群2中 B(r)=Boer2. 的第1个个体进行比较,选择其中最小完工时间较 式中:B,表示2个个体距离为0时,当前个体对另 小的个体,作为新种群的第1个个体;种群1中的第 外1个个体的吸引力,y为介质的吸收率。 2个个体和种群2中的第2个个体进行比较,选择 在该算法中,2个个体之间的距离r采用欧式 其中最小完工时间较小的一个,作为新种群的第2 距离.个体i向着比它更亮的个体j进行更新的公式 个个体;依此类推,新种群作为初始化种群.此外,由 定义为 于NEH(Nawaz-Enscore-Ham)[o启发式算法是目前 女=+Be(g-x)+a(R-2. (7) 求解流水线调度最有效的启发式方法之一,因此,在 初始化种群时还引入了NEH的思想.种群的第1个 式中:x:和分别表示个体i和个体j在整个种群 个体由NEH启发式方法生成,其他个体由双重初始 更新之前的位置,x表示个体i朝着比自己更亮的 化方式生成,从而使得算法有一个较好的初始化 个体j更新之后的位置,"代表个体i和个体j之间 环境 的距离,Be表示个体j对个体i的吸引力,a是 目前,人们已经发现很多昆虫存在莱维飞行 一个[0,1]内的随机数,R为一个随机数生成函数, (L6 yflights)a,且莱维飞行已经应用于优化领 生成[0,1]内的随机数 域,并取得了预期的良好效果.为了增强算法的全局 3 改进的萤火虫算法求解阻塞流水线 搜索性能,避免种群陷入局部最优,在萤火虫算法的 搜索过程中,如果当前个体找不到比自己更优的个 调度问题 体时,选择莱维飞行代替原算法中的随机飞行.此 虽然萤火虫算法在函数优化方面表现出了较好 外,对于那些种群中非最优的个体,对它们的飞行公 的计算性能,但是,它在求解阻塞流水线调度问题中 式进行改进:当它们发现比自己更亮的个体时,首先 仍然存在早熟现象,为了提高算法的寻优性能,本文 由系统产生一个随机数q,如果q小于0.5,则按照 对萤火虫算法进行了一些改进, 式(8)进行更新:否则,仍采用式(7)对个体的位置 萤火虫算法应用于求解阻塞流水线调度问题 进行更新 时,首先调到的问题就是如何将实数编码离散化.本 文提出一种最小排序方法,这种方法可以将个体的 对=对+Be(与-对)+a(R-2》.(8) 实数编码形式转化成离散的调度序列.该方法对初 式中:x仍然表示个体j在整个种群更新之前的位 始化后的实数序列从小到大进行排序,它们的排序 置,x表示的是第i个个体朝着前j-1个体中比自 序号构成一个离散序列,将这个序列作为该实数序 己亮的个体更新之后的新位置,x表示x朝着比自 列对应的离散调度序列.如表2所示,0.43是实数 己亮的个体j更新之后的位置,「代表个体i和个体 编码序列中最小的实数,从小到大排序后,它的序号应 j之间的距离,Be表示个体j对个体i的吸引力. 该为1;同理,0.91是实数序列中最大的,因此其序号为 可以看出,式(8)是实时更新的,式(7)仅仅依赖于 5.新生产的序列{4,2,5,1,3}作为实数序列{0.85, 整个种群移动之前的个体位置.这样的飞行更新方 0.56,0.91,0.43,0.76}对应的离散调度序列. 式能够增加飞行的随机性,有利于保持种群的多样 表2个体表示形式 性,增大种群搜索空间. Table 2 The presentation of an object 为了加速种群的收敛,本文还提出了一种α的 维数 X 更新方式,使得α随着迭代次数逐渐减小,更新公 1 0.85 4 式为 2 0.56 0 式中:o选用0.9,t为迭代次数. 0.91 对于一个调度序列而言,目前主要有3种产生 0.43 新序列的方法:插入、交换和逆序6.其中,插人方 J 0.76 法被证明为最适合产生一个新序列的方法.为了加 其次,在种群初始化时,本文设计了一种双重初 强萤火虫算法的局部搜索能力,本文引入了一个局 始化方法:分别生成2个种群,计算2个种群中每个 部搜索算法.局部搜索算法可以描述如下):

·36 智能系统学报 第8卷 1)选定调度序列π={,m2,…,n},i=0j=1. 4.1数据集 2)i=i+1,如果i>n,则i=i-n 本文采用著名的Taillard数据集作为测试实 3)把π赋给中间序列U,把序列U中的第i个 例,该数据集包含12个子集,每个子集包含10个测 作业π:从U中去除,将π:插入U中所有可以插入 试实例.为了检验算法的有效性,从这些子集中选取 的位置,选取其中最好的调度序列π. 了部分具有代表性的实例作为测试数据,所选实例 4)分别求解序列π和序列U的最小完工时 涵盖了从20个作业5台机器到200个作业10台机 间f(π)和f(U),如果f(π)<f(U),则U= 器不同难度的测试实例,具有很好的代表性.所选实 xj=0;否则j=j+1. 例的规模如表3所示.例如在T04实例中,20×5 5)如果j≤n,转步骤2);否则,算法结束,m'=U. 表示20个作业在5台机器上运行. 在这个算法中,i和j用来控制循环次数,没有 实际意义,是作业的数目,也是解的维数 表3实例规模 这种局部搜索算法的好处在于:首先,局部搜索 Table 3 The size of instances 策略并没有直接对所选序列进行修改,而是应用于 实 例 规模 实例 规模 一个中间序列U,避免算法陷入局部最优;其次,在 Ta04 20×5 Ta54 50×20 每次搜索过程中,只有找到更好的解时,才对中间序 Tal4 20×10 Ta64 100×5 列进行更新,有利于算法逐步向更优的解靠近.因 Ta24 20×20 Ta74 100×10 此,局部搜索算法在一定程度上加强了萤火虫算法 Ta34 50×5 Ta84 100×20 的局部搜索能力, 改进后的萤火虫算法和原算法相比,初始化部 Ta44 50×10 Ta94 200×10 分使得算法有一个较好的搜索域,局部搜索算法又 进一步提高了算法的搜索性能.改进后的萤火虫算 4.2 实验结果及分析 法求解阻塞流水线调度问题的步骤如下: 实验中,种群大小为10,最大迭代次数tm为 1)初始化种群,包括迭代次数t=0、最大迭代 100,、B、Y的设置参考了萤火虫算法相关文献 次数t、随机参数、个体吸引力B,、介质吸收率 [9,13-14]中的参数设置,a6设置为0.9,B。设置为 Y、局部搜索概率p. 1.0,y设置为0.9,局部搜索概率p设置为0.2.对 2)按照式(1)~(5)计算每个个体的最小完工 于前6个实例,每个实例进行10次独立实验;对于 时间. 后4个实例,由于数据量较大,每个个体进行5次独 3)萤火虫算法 立实验.为了测试改进后的萤火虫算法在阻塞流水 ①更新; 线调度问题中的性能,还对同等条件下的未改进的 ②对当前个体,如果有比自己更亮的个体,则按 萤火虫算法和标准的粒子群算法进行了测试.表4 照改进后的更新方式,利用式(7)或(8)对当前个体 为未改进的萤火虫算法的测试结果,表5为标准粒 的位置进行更新;否则,采用莱维飞行对个体位置进 子群算法的测试结果,改进的萤火虫算法的测试结 行更新 果列于表6中.其中,在标准的粒子群算法中, 4)按照式(1)~(5)计算每个个体的最小完工 2个学习因子c1和c2取值为2,惯性权重w设置 时间. 为0.7 5)系统产生一个随机数,如果这个随机数小于 由表4、5可以看出,无论是最小值、最大值,还 局部搜索概率P,则对种群个体进行局部搜索,并更 是平均值,萤火虫算法的求解结果普遍优于标淮粒 新种群。 子群算法.对比表4和表6,可以发现,改进的萤火 6)t=t+1,如果t≥tmm或算法达到其他标准,则 虫算法在求解效果上要远远优于基本的萤火虫算 算法终止;否则,转步骤3) 法,而且求解结果更加稳定.综合表4~6,改进后的 4仿真实验 萤火虫算法的求解效果明显优于基本的萤火虫算法 和标准的粒子群算法.并且随着种群的增大,这种差 实验所用PC机的处理器为AMD Athlon64X2 距更加明显,充分体现了算法的有效性,而且新算法 3600+1.91GHz,内存为960MB,编程工具采用 的求解效果更加稳定. Matlab 7.0
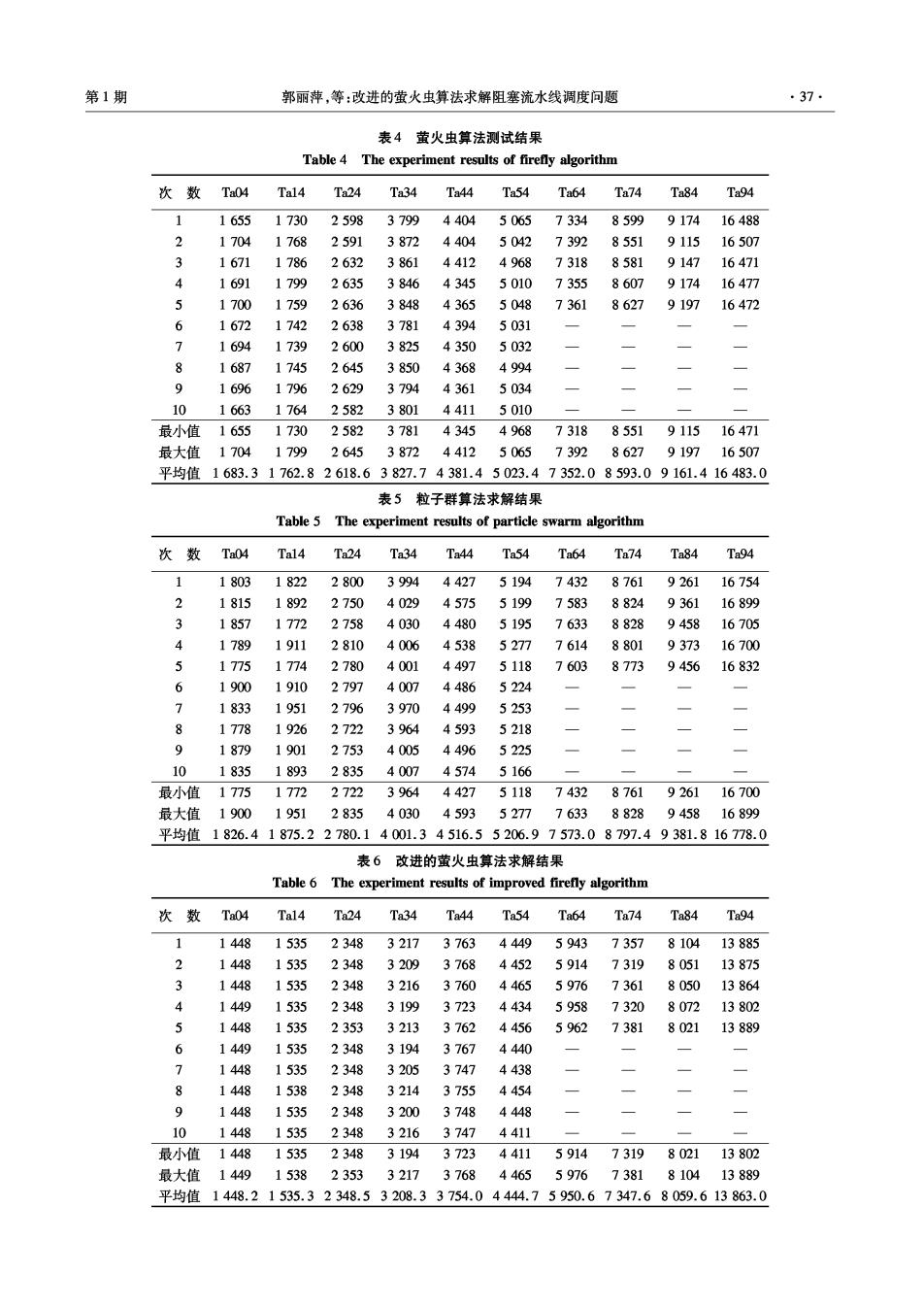
第1期 郭丽萍,等:改进的萤火虫算法求解阻塞流水线调度问题 ·37 表4萤火虫算法测试结果 Table 4 The experiment results of firefly algorithm 次数 Ta04 Tal4 Ta24 Ta34 Ta44 Ta54 Ta64 Ta74 Ta84 Ta94 1655 1730 2598 37994404 5065 7334 8599 9174 16488 1704 1768 2591 3872 4404 5042 7392 8551 9115 16507 3 16711786 2632 38614412 4968 7318 8581 9147 16471 16911799 2635 38464345 5010 7355 8607 9174 16477 1700 1759 2636 38484365 5048 7361 8627 9197 16472 6 1672 1742 2638 3781 4394 5031 1694 1739 2600 3825 4350 5032 8 16871745 2645 385043684994 9 169617962629379443615034 10 166317642582380144115010 最小值1655 1730258237814345496873188551 911516471 最大值1704 1799264538724412506573928627919716507 平均值1683.31762.82618.63827.74381.45023.47352.08593.09161.416483.0 表5粒子群算法求解结果 Table 5 The experiment results of particle swarm algorithm 次数Ta04 Tal4 Ta24 Ta34 Ta44 Ta54 Ta64 Ta74 Ta84 Ta94 1803 1822 2800 3994 4427 5194 7432 8761 9261 16754 2 1815 1892 2750 4029 4575 5199 7583 8824 9361 16899 1857 1772 2758 4030 4480 5195 7633 8828 9458 16705 1789 1911 2810 40064538 5277 7614 8801 9373 16700 J 1775 17742780 40014497 51187603 8773 9456 16832 6 1900 19102797 40074486 5224 18331951 279639704499 5253 8 177819262722 39644593 5218 1879 19012753 4005 4496 5225 10 1835 18932835400745745166 最小值1775177227223964442751187432 8761 926116700 最大值 1900195128354030459352777633 8828 9458 16899 平均值1826.41875.22780.14001.34516.55206.97573.08797.49381.816778.0 表6改进的萤火虫算法求解结果 Table 6 The experiment results of improved firefly algorithm 次数 Ta04 Tal4 Ta24 Ta34 Ta44 Ta54 Ta64 Ta74 Ta84 Ta94 1 14481535 23483217376344495943 7357 8104 13885 2 14481535 2348 32093768 4452 59147319 8051 13875 3 14481535 2348321637604465 5976 7361 8050 13864 4 1449 1535 2348 3199 37234434 59587320 8072 13802 5 14481535 235332133762 4456 5962 7381 8021 13889 6 14491535 2348319437674440 > 14481535 23483205 3747.4438 P 14481538234832143755 4454 9 144815352348320037484448 10 144815352348 321637474411 最小值1448 1535 23483194 3723 4411 5914 7319 802113802 最大值1449 15382353 3217 37684465 5976 73818104 13889 平均值1448.21535.32348.53208.33754.04444.75950.67347.68059.613863.0

·38 智能系统学报 第8卷 flow shop scheduling problems[J].Computers &Operations 5 结束语 Research,2010,37(3):509-520. 本文提出了一种改进的萤火虫算法,设计了双 [8]YANG Xinshe.Nature-inspired metaheuristic algorithms 重初始化方法,引入了EH启发式方法,重新设计 [M].Frome,UK:Luniver Press,2008:81-96 了算法中个体位置的更新方式,并引入了莱维飞行 [9]YANG Xinshe.Firefly algorithms for multimodal optimiza- tion[C]//Proceedings of the 5th Intemational Conference 来增大种群的搜索域.在求解阻塞流水线调度问题 on Stochastic Algorithms:Foundations and Applications. 时,设计了一种将实数编码离散化的机制,实现了实 Berlin/Heidelberg,Germany:Springer-Verlag,2009:169- 数编码算法对离散化问题的求解.此外,本文还引入 178. 了一种局部搜索算法来加强算法的局部搜索能力. [10]NAWAZ M,ENSCORE EE J,HAM I.A heuristic algo- 实验结果表明,改进后的萤火虫算法在求解阻塞流 rithm for the m-machine,n-job flow shop sequencing prob- 水线调度问题时,性能有了明显提高,而且随着问题 1em[J].0meg,1983,11(1):91-95. 规模的增大,这种提高更加明显,体现了算法的有效 [11]BROWN C T,LIEBOVITCH L S,GLENDON R.Levy 性和鲁棒性。 flights in Dobe Ju/'hoansi foraging patterns[J].Human 由于阻塞流水线调度问题具有很重要的实际应 Ecology,2007,35(1):129-138. 用价值,因此将来的工作会考虑把其他优秀的算法 [12]PAVLYUKEVICH I.Levy flights,non-local search and simulated annealing[J].Joumal of Computational Phys- 引入到这个问题中进行求解.另外,由于元启发式算 ic8,2007,226(2):1830-1844. 法普遍存在计算量大的问题,将来的工作还应该考 [13 ]YANG Xinshe.Firefly algorithm,Levy flights and global 虑如何提高求解效率。 optimization[C]//Research and Development in Intelligent 参考文献: Systems XXVI.London,UK:Springer,2010:209-218. [14]YANG Xinshe.Firefly algorithm,stochastic test functions [1]ALLAHYERDI A,NG C T,CHENG T C E,et al.A sur- and design optimization[J].International Joural of Bio- vey of scheduling problems with setup times or costs[J]. Inspired Computation,2010,2(2):78-84. European Journal of Operational Research,2008,187(3): 作者简介: 985-1032, 郭丽萍,女,1989年生,硕士研究 [2]MCCORMICK S T,PINEDO M L,SHENKER S,et al.Se- 生,主要研究方向为智能规划、智能信 quencing in an assembly line with blocking to minimize cy- 息处理. cle time J].Operations Research,1989,37(6):925- 935. [3]RONCONI D P.A note on constructive heuristics for the flowshop problem with blocking[J].International Joumal of Production Economics,2004,87(1):39-48. 李向涛,男,1987年生,博士研究 [4]CARAFFA V,IANES S,BAGCHI T P,et al.Minimizing 生,主要研究方向为智能规划、智能信 makespan in a blocking flowshop using genetic algorithms 息处理,发表学术论文多篇。 [J].International Journal of Production Economics,2001, 70(2):101-115. [5]RONCONI D P.A branch-and-bound algorithm to minimize the makespan in a flowshop with blocking[J].Annals of Operations Research,2005,138(1):53-65. 谷文祥,男,1947年生,教授,博士 [6]GRABOWSKI J,PEMPERA J.The permutation flow shop 生导师,主要研究方向为智能规划与规 problem with blocking.A tabu search approach[J].Ome 划识别、形式语言与自动机理论、模糊 g,2007,35(3):302311. 数学及其应用.主持国家自然科学基金 [7]WANG Ling,PAN Quanke,SUGANTHAN P N,et al.A no- 项目3项,发表学术论文100余篇. vel hybrid discrete differential evolution algorithm for blocking