
第8卷第6期 智能系统学报 Vol.8 No.6 2013年12月 CAAI Transactions on Intelligent Systems Dec.2013 D0:10.3969/j.issn.1673-4785.201211017 网s络出版地址:http:/www.cnki.net/kcms/detail/23.1538.TP.20131012.1814.005.html 基于压缩感知的监控视频重构 李昂,马强2,岑翼刚,赵瑞珍,岑丽辉 (1.北京交通大学信息科学研究所,北京100044;2.宜昌供电公司电能计量中心,湖北宜昌443000:3.中南大学信 息科学与工程学院,湖南长沙410083) 摘要:传统对视频先采样再压缩的方法极大地浪费了硬件资源,针对这一问题,基于压缩感知理论提出了一种对 监控视频采样及重构的方法该方法先获得帧间差值,再将差值投影到小波稀疏域后进行压缩采样选取每一分组中 的中间帧作为关键帧,对关键帧不进行处理,完全保留所有采样点.恢复时利用关键帧和差值可以得到初步重构的视 频序列,最后通过运动估计和运动补偿得到优化实验结果表明,与仅使用压缩感知对差分帧进行重构的方法相比, 该方法对监控视频重构帧序列图像的平均峰值信噪比有较大的提升,且受采样点数影响较小,具有很好的鲁棒性 关键词:压缩感知:监控视频;关键帧;帧间差值;运动补偿 中图分类号:TP18:TN911.72文献标志码:A文章编号:1673-4785(2013)06-0512-05 中文引用格式:李昂,马强,岑翼刚,等.基于压缩感知的监控视频重构[J].智能系统学报,2013,8(6):512-516. 英文引用格式:LI Ang,MA Qiang,CEN Yigang,etal.Reconstruction of surveillance video based on compression sensing[J]. CAAI Transactions on Intelligent Systems,2013,8(6):512-516. Reconstruction of surveillance video based on compressed sensing LI Ang',MA Qiang?,CEN Yigang',ZHAO Ruizhen',CEN Lihui? (1.Institute of Information Science,Beijing Jiaotong University,Beijing 100044,China;2.Electric Energy Measurement Center, Yichang Power Supply Company,Yichang 443000,China;3.Institute of Information Science and Engineering,Central South Universi- ty,Changsha 410083,China) Abstract:The traditional first-compression-then-sampling method used for video greatly wastes hardware resources.In order to solve this problem,a sampling and reconstruction method used for the surveillance video is proposed based on compressed sensing.With this method,first,the interframe difference is calculated and projected to the sparse do- main of the wavelet,then the wavelet coefficients are sensed by the sensing matrix.The middle frame in every group is taken as the key frame,which is not processed,and all sampling points are completely preserved.In the stage of re- covery,the preliminary reconstruction of the video sequence can be obtained by using the key frames and interframe difference.Finally,the optimization is realized by motion estimation and motion compensation.The experimental re- sults show that,compared with the reconstruction for difference frames by only using compressed sensing,this method can greatly lift the mean peak signal-noise ratio of the sequence image on the reconstruction frames of a surveillance video.In addition,the influence caused by the quantity of the sampling points is small,and the robustness is excel- lent. Keywords:compressed sensing;surveillance video;key frame;interframe difference;motion compensation 随着社会的进步和通信技术的不断发展,人与人之间的视频传输变得越来越频繁,这就对通信过 程中的数据存储和传输设备提出了更高的要求.传 收稿日期:2012-11-12.网络出版日期:2013-10-12. 基金项目:国家自然科学基金资助项目(61272028,61104078, 统的奈奎斯特采样定理指出,信号的采样频率必须 61073079);中央高校基本科研业务费资助项目 大于或等于信号带宽的2倍,才能准确地恢复和重 (2013BZ003):上海交通大学系统控制与信息处理教育 部重点实验室开放基金资助项目(SCP20110O9);高等学 构出原信号.显然,对于视频信号的传输,奈奎斯特 校博士学科点专项科研基金资助项目(20110162120045, 20120009110008). 采样定理具有很大的局限性。 近年来,由Donoho、Candes)及Tao等[2提出 通信作者:岑翼刚.E-mail:yen@bjtu.edu,cem
第 8 卷第 6 期 智 能 系 统 学 报 Vol.8 №.6 2013 年 12 月 CAAI Transactions on Intelligent Systems Dec. 2013 DOI:10.3969 / j.issn.1673⁃4785.201211017 网络出版地址:http: / / www.cnki.net / kcms/ detail / 23.1538.TP.20131012.1814.005.html 基于压缩感知的监控视频重构 李昂1 ,马强2 ,岑翼刚1 ,赵瑞珍1 ,岑丽辉3 (1.北京交通大学 信息科学研究所,北京 100044; 2.宜昌供电公司 电能计量中心,湖北 宜昌 443000; 3.中南大学 信 息科学与工程学院,湖南 长沙 410083) 摘 要:传统对视频先采样再压缩的方法极大地浪费了硬件资源,针对这一问题,基于压缩感知理论提出了一种对 监控视频采样及重构的方法.该方法先获得帧间差值,再将差值投影到小波稀疏域后进行压缩采样.选取每一分组中 的中间帧作为关键帧,对关键帧不进行处理,完全保留所有采样点.恢复时利用关键帧和差值可以得到初步重构的视 频序列,最后通过运动估计和运动补偿得到优化.实验结果表明,与仅使用压缩感知对差分帧进行重构的方法相比, 该方法对监控视频重构帧序列图像的平均峰值信噪比有较大的提升,且受采样点数影响较小,具有很好的鲁棒性. 关键词:压缩感知;监控视频;关键帧;帧间差值;运动补偿 中图分类号: TP18;TN911.72 文献标志码:A 文章编号:1673⁃4785(2013)06⁃0512⁃05 中文引用格式:李昂,马强,岑翼刚,等. 基于压缩感知的监控视频重构[J]. 智能系统学报, 2013, 8(6): 512⁃516. 英文引用格式:LI Ang, MA Qiang, CEN Yigang, et al. Reconstruction of surveillance video based on compression sensing[ J]. CAAI Transactions on Intelligent Systems, 2013, 8(6): 512⁃516. Reconstruction of surveillance video based on compressed sensing LI Ang 1 , MA Qiang 2 , CEN Yigang 1 , ZHAO Ruizhen 1 , CEN Lihui 3 (1. Institute of Information Science, Beijing Jiaotong University, Beijing 100044, China; 2. Electric Energy Measurement Center, Yichang Power Supply Company, Yichang 443000, China; 3. Institute of Information Science and Engineering, Central South Universi⁃ ty, Changsha 410083, China) Abstract:The traditional first⁃compression⁃then⁃sampling method used for video greatly wastes hardware resources. In order to solve this problem, a sampling and reconstruction method used for the surveillance video is proposed based on compressed sensing. With this method, first, the interframe difference is calculated and projected to the sparse do⁃ main of the wavelet,then the wavelet coefficients are sensed by the sensing matrix.The middle frame in every group is taken as the key frame, which is not processed, and all sampling points are completely preserved. In the stage of re⁃ covery, the preliminary reconstruction of the video sequence can be obtained by using the key frames and interframe difference. Finally, the optimization is realized by motion estimation and motion compensation. The experimental re⁃ sults show that, compared with the reconstruction for difference frames by only using compressed sensing, this method can greatly lift the mean peak signal⁃noise ratio of the sequence image on the reconstruction frames of a surveillance video. In addition, the influence caused by the quantity of the sampling points is small, and the robustness is excel⁃ lent. Keywords:compressed sensing; surveillance video; key frame; interframe difference; motion compensation 收稿日期:2012⁃11⁃12. 网络出版日期:2013⁃10⁃12. 基金项 目: 国 家 自 然 科 学 基 金 资 助 项 目 ( 61272028, 61104078, 61073079); 中 央 高 校 基 本 科 研 业 务 费 资 助 项 目 (2013JBZ003);上海交通大学系统控制与信息处理教育 部重点实验室开放基金资助项目( SCIP2011009);高等学 校博士学科点专项科研基金资助项目(20110162120045, 通信作者:岑翼刚. E⁃mail:ygcen@ bjtu.edu.cn 20120009110008). . 随着社会的进步和通信技术的不断发展,人与 人之间的视频传输变得越来越频繁,这就对通信过 程中的数据存储和传输设备提出了更高的要求.传 统的奈奎斯特采样定理指出,信号的采样频率必须 大于或等于信号带宽的 2 倍,才能准确地恢复和重 构出原信号.显然,对于视频信号的传输,奈奎斯特 采样定理具有很大的局限性. 近年来,由 Donoho、Candes [1] 及 Tao 等[2] 提出

第6期 李昂,等:基于压缩感知的监控视频重构 ·513· 了一种新的信息获取理论称作压缩感知(com- 当矩阵中满足RP准则时,重构K-稀疏系数 pressed sensing或compressive sampling,CS).这一理 a:最直接的方法是通过在l。范数下求解式(2)的最 论的着眼点放在了信号的稀疏性,即信号在合适的 优化问题: 稀疏基下可以变换到相应的稀疏域,从而呈现出信 min‖awlo,s.t.y=Φ乎a, (3) 号的稀疏性.另外,对于如何将信号在稀疏域进行压 从而得到稀疏系数:的估计.由于式(3)求解时,方 缩感知处理,很多算法被提出,例如利用峰值变 程个数远小于未知数的个数,即。范数下的求解是 换)、利用单层小波变换[等. NP-Hard问题.Donoho等t)指出,当Φ和亚不相关 在处理监控视频信号时,还要充分考虑到视频中 时,求解一个更加简单的,范数优化问题会产生相 帧与帧之间的相关性.对相邻2帧做差,得到的差值 同的解.即。极小化问题可转化为L,范数下的最小 图像本身就具有一定的稀疏性.另外,在帧图像重构 化问题: 的过程中,可以通过参考帧图像对当前帧图像进行运 min la‖,s.ty=ΦΨae (4) 动估计和运动补偿,从而进一步提高视频重构质量 通过求解式(4),可以得到稀疏域重建的结果 1压缩感知理论 求解(,范数下极小化问题常用算法有3类:贪婪追 踪法、凸松弛法和组合算法,例如匹配追踪法(matc- 考虑一个可压缩实值信号f(∫∈Rx1),信号 hing pursuit,MP)s)]、正交匹配追踪法(orthogonal 长度为N,则该信号可以由一组正交基展开亚= matching pursuit,OMP)[9)、梯度投影法(gradient [1中2…中w],如式(1): projection,GP)【uo、链式追踪法[u等 N f=∑,a,或f=a (1) =1 2基于压缩感知的监控视频恢复 式(1)为正交变换的反变换,正变换为α=∫ 监控视频的特点是背景基本不变,视频图像数 其中,=亚=L,亚∈Cxw,I为单位阵,a是 据有着极大的相关性,也就是有大量的冗余信息.对 信号f在亚下的稀疏表示.若式(1)中的α只有K 于监控视频,背景不是重要信息,压缩感知主要是针 个非零元素(N≥K),其余的元素为0或者接近于 对监控视频中的运动物体进行处理的. 0,则认为该信号是稀疏的: 对于YUV视频数据来说,本文研究的是对其Y 信号可稀疏表示是压缩感知的先验条件.在已知 分量所构成的部分进行处理首先,将视频序列进行 信号是可压缩的前提下,压缩感知过程可分为如下2 分组,每组包含相同的帧数.为了达到更好的恢复效 步[1: 果,在关键帧的选取上,选取一组帧图像(奇数个)的 1)设计一个大小为M×N(MW)的测量矩阵Φ 中间帧作为关键帧帧与帧之间差值的获取比较简 对稀疏信号进行观测,得到M维的测量向量, 单,即后一帧减去前一帧的结果作为差分的结果对 测量值y是一个M维向量,这样使测量对象从 差值图像运用压缩感知技术进行采样,而关键帧不进 N维降为M维.观测过程是非自适应的,即测量矩阵 行压缩感知处理,完全保留所有采样点.另外也可先 的选择不依赖于信号∫测量矩阵的设计要求信号从 对帧图像先感知,再做差分,此时则应该对2帧图像 ∫转换为y的过程不会破坏原始信号的信息,否则, 采用相同的测量矩阵,即应有式(5)成立: 重构是不可能的[).由于信号∫是可稀疏表示的,测 (f1-∫2)=f-时2: (5) 量过程可以表示为 式中:∫,和∫2是相邻的2帧.由式(5)可知,对2帧 y=Φf=Φa=O. (2) 图像的差值采样等效于分别对2帧图像先采样再进 式中:O是一个M×N矩阵.若④满足有限等距性质 行差分[2」 (restricted isometry property,RIP),即对于任意K-稀 由于监控视频中每一帧图像的背景总是基本不 疏信号∫和常数6∈(0,1),矩阵④满足: 变的,当场景中的物体运动比较缓慢或者运动物体尺 寸比较小时,帧与帧的差值在空域就具备稀疏的性 1-δ4≤ f3 ≤1+8, 质.但当场景中物体运动比较迅速或者运动的物体尺 则K个系数能够从M个测量值中准确地被重构. 寸比较大时,空域的稀疏性将急剧下降因此,为了使 RP性质的等价条件是测量矩阵Φ和稀疏基亚不 差值都具有稀疏的性质,本论文对差值进行进一步处 相关 理,即利用二维小波变换,将差值图像投影到比较稀 2)由M维的测量向量重构信号. 疏的域
了一种新的信息 获 取 理 论 称 作 压 缩 感 知 ( com⁃ pressed sensing 或 compressive sampling, CS).这一理 论的着眼点放在了信号的稀疏性,即信号在合适的 稀疏基下可以变换到相应的稀疏域,从而呈现出信 号的稀疏性.另外,对于如何将信号在稀疏域进行压 缩感知处理, 很多算法被提出, 例如利用峰值变 换[3] 、利用单层小波变换[4]等. 在处理监控视频信号时,还要充分考虑到视频中 帧与帧之间的相关性.对相邻 2 帧做差,得到的差值 图像本身就具有一定的稀疏性.另外,在帧图像重构 的过程中,可以通过参考帧图像对当前帧图像进行运 动估计和运动补偿,从而进一步提高视频重构质量. 1 压缩感知理论 考虑一个可压缩实值信号 f( f ∈ R N×1 ) ,信号 长度为 N ,则该信号可以由一组正交基展开 Ψ = ψ1 ψ2 … ψN [ ] ,如式(1): f = ∑ N i = 1 ψiαi 或 f = Ψα. (1) 式(1)为正交变换的反变换,正变换为 α= Ψ H f. 其中,ΨΨ H = Ψ HΨ= Ι,Ψ∈C N×N , Ι 为单位阵,α 是 信号 f 在 Ψ 下的稀疏表示.若式(1)中的 α 只有 K 个非零元素(N≫K),其余的元素为 0 或者接近于 0,则认为该信号是稀疏的. 信号可稀疏表示是压缩感知的先验条件.在已知 信号是可压缩的前提下,压缩感知过程可分为如下 2 步[5] : 1)设计一个大小为 M×N(M≪N) 的测量矩阵 Φ 对稀疏信号进行观测,得到 M 维的测量向量. 测量值 y 是一个 M 维向量,这样使测量对象从 N 维降为 M 维.观测过程是非自适应的,即测量矩阵 的选择不依赖于信号 f.测量矩阵的设计要求信号从 f 转换为 y 的过程不会破坏原始信号的信息,否则, 重构是不可能的[6] .由于信号 f 是可稀疏表示的,测 量过程可以表示为 y = Φf = ΦΨα = Θα. (2) 式中:Θ 是一个 M×N 矩阵.若 Φ 满足有限等距性质 (restricted isometry property,RIP),即对于任意 K⁃稀 疏信号 f 和常数 δk∈(0,1),矩阵 Φ 满足: 1 - δk ≤ ‖Φf‖2 2 ‖f‖2 2 ≤ 1 + δk, 则 K 个系数能够从 M 个测量值中准确地被重构. RIP 性质的等价条件是测量矩阵 Φ 和稀疏基 Ψ 不 相关. 2)由 M 维的测量向量重构信号. 当矩阵 Φ 满足 RIP 准则时,重构 K ⁃稀疏系数 α 最直接的方法是通过在 l 0 范数下求解式(2)的最 优化问题: min α ‖α‖l0 ,s.t. y = ΦΨα, (3) 从而得到稀疏系数 α 的估计.由于式(3)求解时,方 程个数远小于未知数的个数,即 l 0 范数下的求解是 NP⁃Hard 问题.Donoho 等[7] 指出,当 Φ 和 Ψ 不相关 时,求解一个更加简单的 l 1 范数优化问题会产生相 同的解.即 l 0 极小化问题可转化为 l 1 范数下的最小 化问题: min α ‖α‖l1 ,s.t. y = ΦΨα. (4) 通过求解式(4),可以得到稀疏域重建的结果. 求解 l 1 范数下极小化问题常用算法有 3 类:贪婪追 踪法、凸松弛法和组合算法,例如匹配追踪法(matc⁃ hing pursuit, MP ) [8] 、正交匹配追踪法( orthogonal matching pursuit, OMP ) [9] 、 梯 度 投 影 法 ( gradient projection, GP) [10] 、链式追踪法[11]等. 2 基于压缩感知的监控视频恢复 监控视频的特点是背景基本不变,视频图像数 据有着极大的相关性,也就是有大量的冗余信息.对 于监控视频,背景不是重要信息,压缩感知主要是针 对监控视频中的运动物体进行处理的. 对于 YUV 视频数据来说,本文研究的是对其 Y 分量所构成的部分进行处理.首先,将视频序列进行 分组,每组包含相同的帧数.为了达到更好的恢复效 果,在关键帧的选取上,选取一组帧图像(奇数个)的 中间帧作为关键帧.帧与帧之间差值的获取比较简 单,即后一帧减去前一帧的结果作为差分的结果.对 差值图像运用压缩感知技术进行采样,而关键帧不进 行压缩感知处理,完全保留所有采样点.另外也可先 对帧图像先感知,再做差分,此时则应该对 2 帧图像 采用相同的测量矩阵,即应有式(5)成立: Φ(f1 - f2 ) = Φf1 - Φf2 . (5) 式中:f1 和 f2 是相邻的 2 帧.由式(5) 可知,对 2 帧 图像的差值采样等效于分别对 2 帧图像先采样再进 行差分[12] . 由于监控视频中每一帧图像的背景总是基本不 变的,当场景中的物体运动比较缓慢或者运动物体尺 寸比较小时,帧与帧的差值在空域就具备稀疏的性 质.但当场景中物体运动比较迅速或者运动的物体尺 寸比较大时,空域的稀疏性将急剧下降.因此,为了使 差值都具有稀疏的性质,本论文对差值进行进一步处 理,即利用二维小波变换,将差值图像投影到比较稀 疏的域. 第 6 期 李昂,等:基于压缩感知的监控视频重构 ·513·
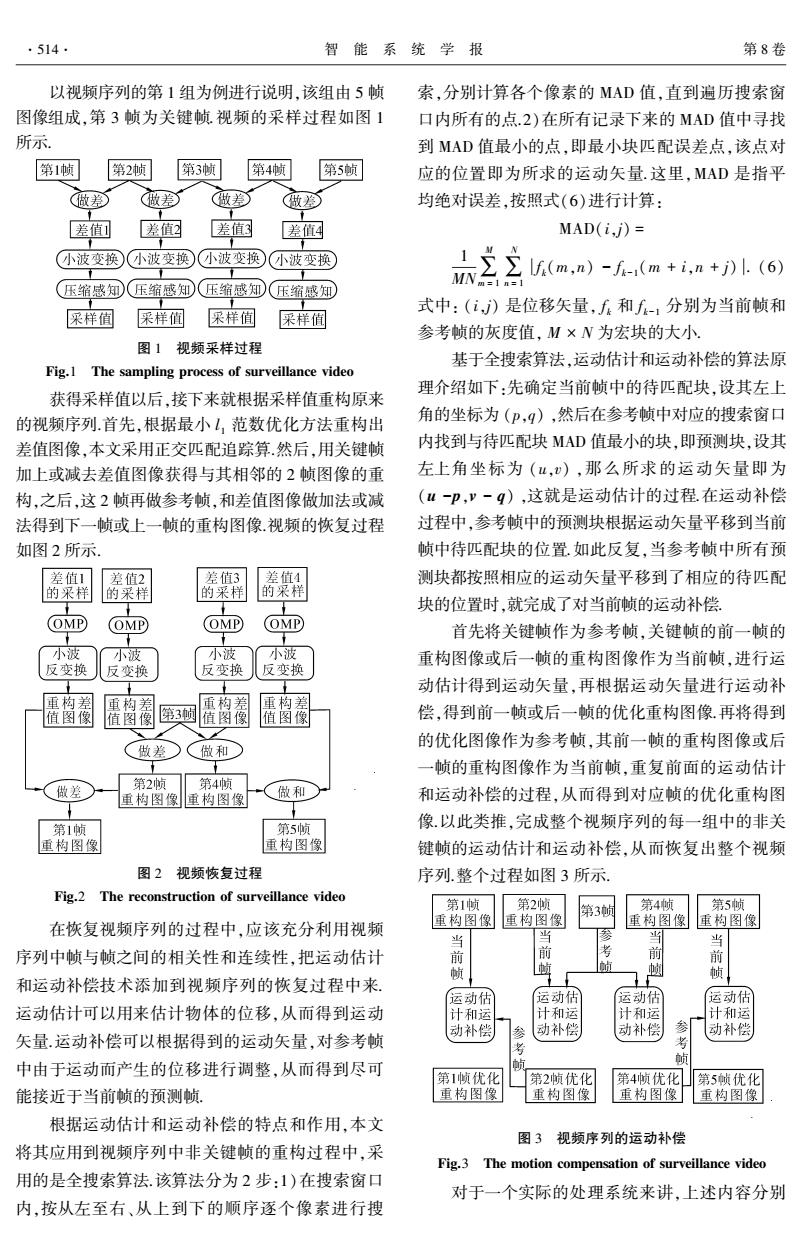
·514 智能系统学报 第8卷 以视频序列的第1组为例进行说明,该组由5帧 索,分别计算各个像素的MAD值,直到遍历搜索窗 图像组成,第3帧为关键帧视频的采样过程如图1 口内所有的点.2)在所有记录下来的MAD值中寻找 所示. 到MAD值最小的,点,即最小块匹配误差点,该点对 第1帧 第2帧 第3帧 第4帧 第5帧 应的位置即为所求的运动矢量.这里,MAD是指平 做差 (做差) 做) (做 均绝对误差,按照式(6)进行计算: 差值1 差值配 差值3 差值✉ MAD(i,j)= 小波变换)小波变换小波变换(小波变换 三(m,)-i-,(m+i,a+》l(6) 压缩感知(压缩感知(压缩感知(压缩感知 式中:(i,》是位移矢量,f和f-1分别为当前帧和 采样值 采样阎 采样囿 采样值 参考帧的灰度值,M×N为宏块的大小 图1视频采样过程 基于全搜索算法,运动估计和运动补偿的算法原 Fig.1 The sampling process of surveillance video 理介绍如下:先确定当前帧中的待匹配块,设其左上 获得采样值以后,接下来就根据采样值重构原来 的视频序列首先,根据最小(,范数优化方法重构出 角的坐标为(P,9),然后在参考帧中对应的搜索窗口 差值图像,本文采用正交匹配追踪算.然后,用关键帧 内找到与待匹配块MAD值最小的块,即预测块,设其 加上或减去差值图像获得与其相邻的2帧图像的重 左上角坐标为(u,),那么所求的运动矢量即为 构,之后,这2帧再做参考帧,和差值图像做加法或减 (u-p,’-q),这就是运动估计的过程在运动补偿 法得到下一帧或上一帧的重构图像视频的恢复过程 过程中,参考帧中的预测块根据运动矢量平移到当前 如图2所示. 帧中待匹配块的位置.如此反复,当参考帧中所有预 差值1 差值2 差值3 差情4 测块都按照相应的运动矢量平移到了相应的待匹配 的采样 的采样 的采样 的采样 块的位置时,就完成了对当前帧的运动补偿 (OMP OMP OMP) OMP 首先将关键帧作为参考帧,关键帧的前一帧的 小波 小波 小波 小波 重构图像或后一帧的重构图像作为当前帧,进行运 反变换 反变换 反变换 反变换 动估计得到运动矢量,再根据运动矢量进行运动补 重构差 重构差 重构差 重构差 值图像 值图像 第3值图像 值图像 偿,得到前一帧或后一帧的优化重构图像再将得到 (做差 的优化图像作为参考帧,其前一帧的重构图像或后 做和 一帧的重构图像作为当前帧,重复前面的运动估计 做差 第2帧 第4帧 重构图像重构图像 、做和 和运动补偿的过程,从而得到对应帧的优化重构图 第1帧 第5帧 像.以此类推,完成整个视频序列的每一组中的非关 重构图像 重构图像 键帧的运动估计和运动补偿,从而恢复出整个视频 图2视频恢复过程 序列.整个过程如图3所示. Fig.2 The reconstruction of surveillance video 第1帧 第2顺 第3帧 第4帧 第5帧 在恢复视频序列的过程中,应该充分利用视频 重构图像 重构图像 重构图像 重构图像 当 当 序列中帧与帧之间的相关性和连续性,把运动估计 前 前 前 帧 和运动补偿技术添加到视频序列的恢复过程中来 运动估 运动估 运动估 运动估 运动估计可以用来估计物体的位移,从而得到运动 计和运 计和运 计和运 计和运 动补偿 参 动补偿 动补偿 动补偿 矢量.运动补偿可以根据得到的运动矢量,对参考帧 中由于运动而产生的位移进行调整,从而得到尽可 的 第1倾优化 第2帧优化 第4帧优化 第5帧优化 能接近于当前帧的预测帧 重构图像 重构图像 重构图像 重构图像 根据运动估计和运动补偿的特点和作用,本文 图3视频序列的运动补偿 将其应用到视频序列中非关键帧的重构过程中,采 Fig.3 The motion compensation of surveillance video 用的是全搜索算法.该算法分为2步:1)在搜索窗口 对于一个实际的处理系统来讲,上述内容分别 内,按从左至右、从上到下的顺序逐个像素进行搜
以视频序列的第 1 组为例进行说明,该组由 5 帧 图像组成,第 3 帧为关键帧.视频的采样过程如图 1 所示. 图 1 视频采样过程 Fig.1 The sampling process of surveillance video 获得采样值以后,接下来就根据采样值重构原来 的视频序列.首先,根据最小 l 1 范数优化方法重构出 差值图像,本文采用正交匹配追踪算.然后,用关键帧 加上或减去差值图像获得与其相邻的 2 帧图像的重 构,之后,这 2 帧再做参考帧,和差值图像做加法或减 法得到下一帧或上一帧的重构图像.视频的恢复过程 如图 2 所示. 图 2 视频恢复过程 Fig.2 The reconstruction of surveillance video 在恢复视频序列的过程中,应该充分利用视频 序列中帧与帧之间的相关性和连续性,把运动估计 和运动补偿技术添加到视频序列的恢复过程中来. 运动估计可以用来估计物体的位移,从而得到运动 矢量.运动补偿可以根据得到的运动矢量,对参考帧 中由于运动而产生的位移进行调整,从而得到尽可 能接近于当前帧的预测帧. 根据运动估计和运动补偿的特点和作用,本文 将其应用到视频序列中非关键帧的重构过程中,采 用的是全搜索算法.该算法分为 2 步:1)在搜索窗口 内,按从左至右、从上到下的顺序逐个像素进行搜 索,分别计算各个像素的 MAD 值,直到遍历搜索窗 口内所有的点.2)在所有记录下来的 MAD 值中寻找 到 MAD 值最小的点,即最小块匹配误差点,该点对 应的位置即为所求的运动矢量.这里,MAD 是指平 均绝对误差,按照式(6)进行计算: MAD(i,j) = 1 MN∑ M m = 1∑ N n = 1 f k(m,n) - f k-1(m + i,n + j) . (6) 式中: (i,j) 是位移矢量, f k 和 f k-1 分别为当前帧和 参考帧的灰度值, M × N 为宏块的大小. 基于全搜索算法,运动估计和运动补偿的算法原 理介绍如下:先确定当前帧中的待匹配块,设其左上 角的坐标为 (p,q) ,然后在参考帧中对应的搜索窗口 内找到与待匹配块 MAD 值最小的块,即预测块,设其 左上角坐标为 (u,v) ,那么所求的运动矢量即为 (u -p,v - q) ,这就是运动估计的过程.在运动补偿 过程中,参考帧中的预测块根据运动矢量平移到当前 帧中待匹配块的位置.如此反复,当参考帧中所有预 测块都按照相应的运动矢量平移到了相应的待匹配 块的位置时,就完成了对当前帧的运动补偿. 首先将关键帧作为参考帧,关键帧的前一帧的 重构图像或后一帧的重构图像作为当前帧,进行运 动估计得到运动矢量,再根据运动矢量进行运动补 偿,得到前一帧或后一帧的优化重构图像.再将得到 的优化图像作为参考帧,其前一帧的重构图像或后 一帧的重构图像作为当前帧,重复前面的运动估计 和运动补偿的过程,从而得到对应帧的优化重构图 像.以此类推,完成整个视频序列的每一组中的非关 键帧的运动估计和运动补偿,从而恢复出整个视频 序列.整个过程如图 3 所示. 图 3 视频序列的运动补偿 Fig.3 The motion compensation of surveillance video 对于一个实际的处理系统来讲,上述内容分别 ·514· 智 能 系 统 学 报 第 8 卷
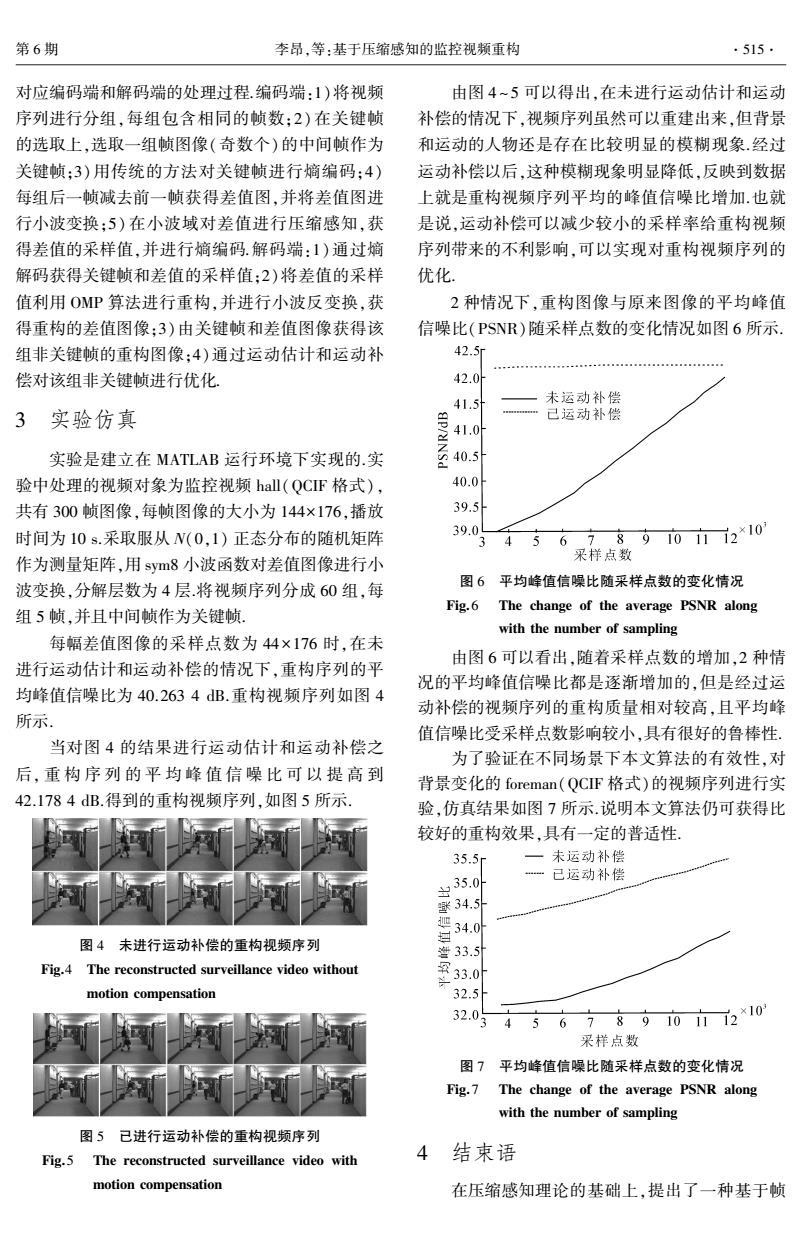
第6期 李昂,等:基于压缩感知的监控视频重构 .515. 对应编码端和解码端的处理过程.编码端:1)将视频 由图4~5可以得出,在未进行运动估计和运动 序列进行分组,每组包含相同的帧数:2)在关键帧 补偿的情况下,视频序列虽然可以重建出来,但背景 的选取上,选取一组帧图像(奇数个)的中间帧作为 和运动的人物还是存在比较明显的模糊现象.经过 关键帧:3)用传统的方法对关键帧进行嫡编码:4) 运动补偿以后,这种模糊现象明显降低,反映到数据 每组后一帧减去前一帧获得差值图,并将差值图进 上就是重构视频序列平均的峰值信噪比增加.也就 行小波变换:5)在小波域对差值进行压缩感知,获 是说,运动补偿可以减少较小的采样率给重构视频 得差值的采样值,并进行嫡编码.解码端:1)通过熵 序列带来的不利影响,可以实现对重构视频序列的 解码获得关键帧和差值的采样值:2)将差值的采样 优化. 值利用OMP算法进行重构,并进行小波反变换,获 2种情况下,重构图像与原来图像的平均峰值 得重构的差值图像:3)由关键帧和差值图像获得该 信噪比(PSNR)随采样点数的变化情况如图6所示 组非关键帧的重构图像:4)通过运动估计和运动补 42.5m 偿对该组非关键帧进行优化: 42.0 41.5 未运动补偿 3实验仿真 己运动补偿 41.0 实验是建立在MATLAB运行环境下实现的.实 验中处理的视频对象为监控视频hall(QCIF格式), 40.0 共有300帧图像,每帧图像的大小为144×176,播放 39.5 时间为10s.采取服从N(0,1)正态分布的随机矩阵 39. 3 45 68910立2×10' 作为测量矩阵,用sym8小波函数对差值图像进行小 采样点数 波变换,分解层数为4层.将视频序列分成60组,每 图6平均峰值信噪比随采样点数的变化情况 Fig.6 The change of the average PSNR along 组5帧,并且中间帧作为关键帧 with the number of sampling 每幅差值图像的采样点数为44×176时,在未 由图6可以看出,随着采样点数的增加,2种情 进行运动估计和运动补偿的情况下,重构序列的平 况的平均峰值信噪比都是逐渐增加的,但是经过运 均峰值信噪比为40.2634dB.重构视频序列如图4 动补偿的视频序列的重构质量相对较高,且平均峰 所示. 值信噪比受采样点数影响较小,具有很好的鲁棒性。 当对图4的结果进行运动估计和运动补偿之 为了验证在不同场景下本文算法的有效性,对 后,重构序列的平均峰值信噪比可以提高到 背景变化的foreman(QCIF格式)的视频序列进行实 42.1784dB.得到的重构视频序列,如图5所示. 验,仿真结果如图7所示说明本文算法仍可获得比 较好的重构效果,具有一定的普适性 35.5r 一 未运动补偿 已运动补偿 35.0 34.5引 把34.0 图4未进行运动补偿的重构视频序列 Fig.4 The reconstructed surveillance video without 33.0 motion compensation 32.5 32.03 45 678910i72*10 采样点数 图7平均峰值信噪比随采样点数的变化情况 Fig.7 The change of the average PSNR along with the number of sampling 图5已进行运动补偿的重构视频序列 Fig.5 The reconstructed surveillance video with 4 结束语 motion compensation 在压缩感知理论的基础上,提出了一种基于帧
对应编码端和解码端的处理过程.编码端:1)将视频 序列进行分组,每组包含相同的帧数;2) 在关键帧 的选取上,选取一组帧图像(奇数个)的中间帧作为 关键帧;3)用传统的方法对关键帧进行熵编码;4) 每组后一帧减去前一帧获得差值图,并将差值图进 行小波变换;5) 在小波域对差值进行压缩感知,获 得差值的采样值,并进行熵编码.解码端:1)通过熵 解码获得关键帧和差值的采样值;2)将差值的采样 值利用 OMP 算法进行重构,并进行小波反变换,获 得重构的差值图像;3)由关键帧和差值图像获得该 组非关键帧的重构图像;4)通过运动估计和运动补 偿对该组非关键帧进行优化. 3 实验仿真 实验是建立在 MATLAB 运行环境下实现的.实 验中处理的视频对象为监控视频 hall(QCIF 格式), 共有 300 帧图像,每帧图像的大小为 144×176,播放 时间为 10 s.采取服从 N(0,1) 正态分布的随机矩阵 作为测量矩阵,用 sym8 小波函数对差值图像进行小 波变换,分解层数为 4 层.将视频序列分成 60 组,每 组 5 帧,并且中间帧作为关键帧. 每幅差值图像的采样点数为 44×176 时,在未 进行运动估计和运动补偿的情况下,重构序列的平 均峰值信噪比为 40.263 4 dB.重构视频序列如图 4 所示. 当对图 4 的结果进行运动估计和运动补偿之 后, 重 构 序 列 的 平 均 峰 值 信 噪 比 可 以 提 高 到 42.178 4 dB.得到的重构视频序列,如图 5 所示. 图 4 未进行运动补偿的重构视频序列 Fig.4 The reconstructed surveillance video without motion compensation 图 5 已进行运动补偿的重构视频序列 Fig.5 The reconstructed surveillance video with motion compensation 由图 4 ~ 5 可以得出,在未进行运动估计和运动 补偿的情况下,视频序列虽然可以重建出来,但背景 和运动的人物还是存在比较明显的模糊现象.经过 运动补偿以后,这种模糊现象明显降低,反映到数据 上就是重构视频序列平均的峰值信噪比增加.也就 是说,运动补偿可以减少较小的采样率给重构视频 序列带来的不利影响,可以实现对重构视频序列的 优化. 2 种情况下,重构图像与原来图像的平均峰值 信噪比(PSNR)随采样点数的变化情况如图 6 所示. 图 6 平均峰值信噪比随采样点数的变化情况 Fig.6 The change of the average PSNR along with the number of sampling 由图 6 可以看出,随着采样点数的增加,2 种情 况的平均峰值信噪比都是逐渐增加的,但是经过运 动补偿的视频序列的重构质量相对较高,且平均峰 值信噪比受采样点数影响较小,具有很好的鲁棒性. 为了验证在不同场景下本文算法的有效性,对 背景变化的 foreman(QCIF 格式)的视频序列进行实 验,仿真结果如图 7 所示.说明本文算法仍可获得比 较好的重构效果,具有一定的普适性. 图 7 平均峰值信噪比随采样点数的变化情况 Fig.7 The change of the average PSNR along with the number of sampling 4 结束语 在压缩感知理论的基础上,提出了一种基于帧 第 6 期 李昂,等:基于压缩感知的监控视频重构 ·515·

.516. 智能系统学报 第8卷 间差值和运动补偿的视频压缩感知重构的方法,该 [8]TROPP J A.Greed is good:algorithmic results for sparse 方法充分利用了帧与帧之间的连续性和相关性,并 approximation[J].IEEE Transactions on Information Theo- 进行了实验,获得了较好的实验效果.在实验仿真 y,2004,50(10):2231-2242. 时,对视频序列的分组比较固定,采样点数比较统 [9]TROPP J A,GILBERT A C.Signal recovery from random 一,并且是对整帧图像进行处理若是采用根据运动 measurements via orthogonal matching pursuit [J].IEEE Transactions on Information Theory,2007,53(12):4655- 剧烈程度自适应分组和自适应采样,并且将帧图像 4666. 分成子块进行处理,效果会进一步得到优化 [10]FIGUEIREDO M A T,NOWAK R D,WRIGHT S J.Gra- 参考文献: dient projection for sparse reconstruction:application to compressed sensing and other inverse problem[J].Journal [1]DONOHO D.Compressed sensing[J].IEEE Transactions of Selected Topics in Signal Processing:Special Issue on on Information Theory,2006,52(4):1289-1306. Convex Optimization Methods for Signal Processing,2007, [2]CANDES E.Compressive sampling[C]//Proceedings of the 1(4):586-598. Intemational Congress of Mathmaticians.Madrid,Spain, [11]GILBERT A C,STRAUSS M J,TROPP J A,et al.Algo- 2006:1433-1452. rithmic linear dimension reduction in the l norm for sparse [3]岑翼刚,岑丽辉.基于峰值变换的信号系数表示及重建 vectors[C]//Proceedings of the 44th Annual Allerton Con- [J].电子与信息学报,2011,33(2):326-331 ference on Communication,Control and Computing.Monti- CEN Yigang,CEN Lihui.Sparse representation and recon- cello,USA,2006:1-27. struction of signals based on the peak transform[J].Journal [12]翟冲.基于压缩感知的视频编码技术研究[D].大连:大 of Electronics and Information Technology,2011,33(2): 连理工大学,2010:18-20. 326-331. Zhai Chong.The research of video coding based on com- [4]岑冀刚,陈晓方,岑丽辉,等.基于单层小波变换的压缩 pressive sensing[D].Dalian:Dalian University of Tech- 感知图像处理[J].通信学报,2010,31(8A):52-55. nology,2010:18-20. CEN Yigang,CHEN Xiaofang,CEN Lihui,et al.Com- 作者简介: pressed sensing based on the single layer wavelet transform 李昂,男,1987年生,硕士研究生, for image processing [J].Journal on Communications, 主要研究方向为压缩感知算法研究、基 2010,31(8A):52-55. 于压缩感知理论的图像处理以及视频 [5]石光明,刘丹华,高大化.压缩感知理论及其研究进展 处理 [J].电子学报,2009(5):1070-1078. SHI Guangming,LIU Danhua,GAO Dahua.Advances in ●⑧④ theory and application of compressed sensing[J].Acta Electronica Sinica,2009 (5):1070-1078. 岑翼刚,男,1978年生,副教授,博 [6]BARANIUK R.A lecture on compressive sensing[J].IEEE 士,主要研究方向为压缩感知、小波分 Signal Processing Magazine,2007,24(4):118-121. 析、信号处理、图像处理,发表学术论文 [7]DONOHO D L,ELAD M,TEMLYAKOV V N.Stable re- 约40篇. covery of sparse overcomplete representations in the pres- ence of noise[J].IEEE Transactions on Information Theo- y,2006,52(1):6-18
间差值和运动补偿的视频压缩感知重构的方法,该 方法充分利用了帧与帧之间的连续性和相关性,并 进行了实验,获得了较好的实验效果.在实验仿真 时,对视频序列的分组比较固定,采样点数比较统 一,并且是对整帧图像进行处理.若是采用根据运动 剧烈程度自适应分组和自适应采样,并且将帧图像 分成子块进行处理,效果会进一步得到优化. 参考文献: [1] DONOHO D. Compressed sensing [ J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289⁃1306. [2]CANDES E. Compressive sampling[C] / / Proceedings of the International Congress of Mathmaticians. Madrid, Spain, 2006: 1433⁃1452. [3]岑翼刚,岑丽辉. 基于峰值变换的信号系数表示及重建 [J]. 电子与信息学报, 2011, 33(2): 326⁃331. CEN Yigang, CEN Lihui. Sparse representation and recon⁃ struction of signals based on the peak transform[J]. Journal of Electronics and Information Technology, 2011, 33( 2): 326⁃331. [4]岑翼刚,陈晓方,岑丽辉,等. 基于单层小波变换的压缩 感知图像处理[J]. 通信学报, 2010, 31(8A): 52⁃55. CEN Yigang, CHEN Xiaofang, CEN Lihui, et al. Com⁃ pressed sensing based on the single layer wavelet transform for image processing [ J ]. Journal on Communications, 2010, 31(8A): 52⁃55. [5]石光明,刘丹华,高大化. 压缩感知理论及其研究进展 [J]. 电子学报, 2009 (5): 1070⁃1078. SHI Guangming, LIU Danhua, GAO Dahua. Advances in theory and application of compressed sensing [ J ]. Acta Electronica Sinica, 2009 (5): 1070⁃1078. [6]BARANIUK R. A lecture on compressive sensing[J]. IEEE Signal Processing Magazine, 2007, 24(4): 118⁃121. [7] DONOHO D L, ELAD M, TEMLYAKOV V N. Stable re⁃ covery of sparse overcomplete representations in the pres⁃ ence of noise[ J]. IEEE Transactions on Information Theo⁃ ry, 2006, 52(1): 6⁃18. [8]TROPP J A. Greed is good: algorithmic results for sparse approximation[ J]. IEEE Transactions on Information Theo⁃ ry, 2004, 50(10): 2231⁃2242. [9]TROPP J A, GILBERT A C. Signal recovery from random measurements via orthogonal matching pursuit [ J ]. IEEE Transactions on Information Theory, 2007, 53(12): 4655⁃ 4666. [10]FIGUEIREDO M A T, NOWAK R D, WRIGHT S J. Gra⁃ dient projection for sparse reconstruction: application to compressed sensing and other inverse problem[ J]. Journal of Selected Topics in Signal Processing: Special Issue on Convex Optimization Methods for Signal Processing, 2007, 1(4): 586⁃598. [11]GILBERT A C, STRAUSS M J, TROPP J A, et al. Algo⁃ rithmic linear dimension reduction in the l 1 norm for sparse vectors[C] / / Proceedings of the 44th Annual Allerton Con⁃ ference on Communication, Control and Computing. Monti⁃ cello, USA, 2006: 1⁃27. [12]翟冲. 基于压缩感知的视频编码技术研究[D].大连:大 连理工大学, 2010: 18⁃20. Zhai Chong. The research of video coding based on com⁃ pressive sensing[D]. Dalian: Dalian University of Tech⁃ nology, 2010: 18⁃20. 作者简介: 李昂,男,1987 年生,硕士研究生, 主要研究方向为压缩感知算法研究、基 于压缩感知理论的图像处理以及视频 处理. 岑翼刚,男,1978 年生,副教授,博 士,主要研究方向为压缩感知、小波分 析、信号处理、图像处理,发表学术论文 约 40 篇. ·516· 智 能 系 统 学 报 第 8 卷