
第8卷第6期 智能系统学报 Vol.8 No.6 2013年12月 CAAI Transactions on Intelligent Systems Dec.2013 D0:10.3969/j.issn.1673-4785.201212060 网络出版地址:http://www.enki..net/kcms/detail/23.1538.TP.20131030.1508.002.html 单、多社区通用的网络舆论突现计算模型 吴渝,李强,刘洪涛 (重庆邮电大学网络智能研究所,重庆400065) 摘要:针对当前网络舆论模型的网络结构构造与实际不符且不能通用,模型规则复杂,运算量较大,考虑因素较局 限等问题,给出了更合理的随机网络构建算法.基于此模型和有界信任模型构造了一种更符合现实的单、多社区通 用的网络舆论突现计算模型,其中考虑了个体记忆、意见领袖和易变个体对舆论的影响.与已有模型的对比分析说 明,该模型算法简单、时间复杂度低、结果更丰富实验结果表明,意见领袖、易变个体、阈值和社区外部连通概率对奥 论形成的时间和舆论的数目有所影响. 关键词:网络舆论:计算模型;有界信任:舆论:突现:单、多社区:随机网络 中图分类号:TP18:TN96711文献标志码:A文章编号:1673-4785(2013)06-0543-08 中文引用格式:吴渝,李强,刘洪涛.单、多社区通用的网络舆论突现计算模型[J】.智能系统学报,2013,8(6):543-550. 英文引用格式:WUYu,LI Qiang,LIU Hongtao.Computation model for the emergence of the network opinion universal for single- community and multi-community[J].CAAI Transactions on Intelligent Systems,2013,8(6):543-550. Computation model for the emergence of the network opinion universal for single and multi-community WU Yu,LI Qiang,LIU Hongtao Institute of Web Intelligence,Chongqing University of Posts and Telecommunications,Chongqing 400065,China) Abstract:The network structure of the contemporary network opinion model does not conform to the actual situations and is not universal.The model rule is complex,the computation volume is large and the factors that may be con- sidered are limited.In this paper,a more reasonable random network structure algorithm is firstly given,and in ad- dition,based on the model and the bounded trust model,a more realistic calculation model for the emergence of the network opinion universal for single and multi-community is established.In the new model,the influence caused by the individual memory,opinion leader,as well as mutable individuals on public opinion is considered.In contrast with the existing model,the new model has the following merits:a simple algorithm,low time complexity and rich results.The experimental results show the opinion leader,mutable individuals,the threshold and the connectivity of a community with the outside affect the formation time of public opinion and the number of public opinion. Keywords:network opinion;computation model;bounded trust;public opinion;emergence;single and multi- community;random network 目前比较著名的舆论演化模型有:基于无界信任 来控制个体间的交互,能够较为真实地反映现实社会 的Sznajd模型)、投票者模型、Galam多数决定模 中人们的交互情况,因此受到舆论研究者的青睐刘 型3d、Hegselmann-Krause模型[)和基于有界信任的 常昱等)在Deffuant模型的基础上引入个体观点的 Deffuant模型[等.其中,Deffuant模型采用信任阈值 不确定性以及个体间的信任因子,仿真实验表明,这 些因素会极大地影响舆论的最终形态及其形成速度 收稿日期:2012-12-27.网络出版日期:2013-10-30 基金项目:国家自然科学基金资助项目(60873079,61040044):重庆市 姚远等[]对刘常昱等提出的模型中的不对称影响函 自然科学基金资助项目(cstc2012jA40027,2009BA2089). 数进行优化,构建了一种基于小世界网络的网络舆论 通信作者:吴渝.E-mail:wuyu@cqupt.eou.cn. 突现模型,仿真实验表明,改进后的模型能够展现更
第 8 卷第 6 期 智 能 系 统 学 报 Vol.8 №.6 2013 年 12 月 CAAI Transactions on Intelligent Systems Dec. 2013 DOI:10.3969 / j.issn.1673⁃4785.201212060 网络出版地址:http: / / www.cnki.net / kcms/ detail / 23.1538.TP.20131030.1508.002.html 单、多社区通用的网络舆论突现计算模型 吴渝,李强,刘洪涛 (重庆邮电大学 网络智能研究所,重庆 400065) 摘 要:针对当前网络舆论模型的网络结构构造与实际不符且不能通用,模型规则复杂,运算量较大,考虑因素较局 限等问题,给出了更合理的随机网络构建算法. 基于此模型和有界信任模型构造了一种更符合现实的单、多社区通 用的网络舆论突现计算模型,其中考虑了个体记忆、意见领袖和易变个体对舆论的影响.与已有模型的对比分析说 明,该模型算法简单、时间复杂度低、结果更丰富.实验结果表明,意见领袖、易变个体、阈值和社区外部连通概率对舆 论形成的时间和舆论的数目有所影响. 关键词:网络舆论;计算模型;有界信任;舆论;突现;单、多社区;随机网络 中图分类号: TP18;TN96711 文献标志码:A 文章编号:1673⁃4785(2013)06⁃0543⁃08 中文引用格式:吴渝,李强,刘洪涛. 单、多社区通用的网络舆论突现计算模型[J]. 智能系统学报, 2013, 8(6): 543⁃550. 英文引用格式:WU Yu, LI Qiang, LIU Hongtao. Computation model for the emergence of the network opinion universal for single⁃ community and multi⁃community[J]. CAAI Transactions on Intelligent Systems, 2013, 8(6): 543⁃550. Computation model for the emergence of the network opinion universal for single and multi⁃community WU Yu, LI Qiang, LIU Hongtao (Institute of Web Intelligence, Chongqing University of Posts and Telecommunications, Chongqing 400065, China) Abstract:The network structure of the contemporary network opinion model does not conform to the actual situations and is not universal. The model rule is complex, the computation volume is large and the factors that may be con⁃ sidered are limited. In this paper, a more reasonable random network structure algorithm is firstly given, and in ad⁃ dition, based on the model and the bounded trust model, a more realistic calculation model for the emergence of the network opinion universal for single and multi⁃community is established. In the new model, the influence caused by the individual memory, opinion leader, as well as mutable individuals on public opinion is considered. In contrast with the existing model, the new model has the following merits: a simple algorithm, low time complexity and rich results. The experimental results show the opinion leader, mutable individuals, the threshold and the connectivity of a community with the outside affect the formation time of public opinion and the number of public opinion. Keywords: network opinion; computation model; bounded trust; public opinion; emergence; single and multi⁃ community; random network 收稿日期:2012⁃12⁃27. 网络出版日期:2013⁃10⁃30. 基金项目:国家自然科学基金资助项目(60873079,61040044);重庆市 自然科学基金资助项目(cstc2012jjA40027,2009BA2089). 通信作者:吴渝. E⁃mail:wuyu@ cqupt.edu.cn. 目前比较著名的舆论演化模型有:基于无界信任 的 Sznajd 模型[1] 、投票者模型[2] 、Galam 多数决定模 型[3⁃4] 、Hegselmann⁃Krause 模型[5] 和基于有界信任的 Deffuant 模型[6]等.其中,Deffuant 模型采用信任阈值 来控制个体间的交互,能够较为真实地反映现实社会 中人们的交互情况,因此受到舆论研究者的青睐.刘 常昱等[7]在 Deffuant 模型的基础上引入个体观点的 不确定性以及个体间的信任因子,仿真实验表明,这 些因素会极大地影响舆论的最终形态及其形成速度. 姚远等[8]对刘常昱等提出的模型中的不对称影响函 数进行优化,构建了一种基于小世界网络的网络舆论 突现模型,仿真实验表明,改进后的模型能够展现更

·544. 智能系统学报 第8卷 为丰富的舆论形态.司夏萌等)将Deffuant模型应用 区之间任意节点之间以外部连通概率P(0p时, 虑个体的个性特征,不能解释群体中具有某些特性 x:(t+1)=x:(t), 的个体对最终舆论结果的影响 (1) x(t+1)=x(t). 针对上述问题,结合突现计算的思想,通过构建 式中:p表示个体间可进行交互的最大观点差值,w 比较符合实际的随机网络,本文在Deffuant模型的 表示个体对交互者的信任程度】 基础上引入了意见领袖、易变个体和网民记忆3个 2随机网络构造算法的改进 因素,建立了单、多社区通用的网络舆论突现计算模 型,并仿真分析了这些改进因素对网络舆论演化过 网民之间的关系网络是根据网民的特性及喜好 程以及最终舆论趋势的影响,以便为网络舆论研究 建立,即考虑网民至少会与一个有较大影响力的网 提供新的思路。 民建立连接.真实网络社区特殊个体的存在,如意见 1相关算法和模型 领袖,对网民关系网络的形成有很大影响.分析已有 的随机网络构建算法,发现其并未考虑上述因素,即 网络舆论演化与突现的2个要素是其赖以传播 目前的随机网络以相等的概率建立节点之间的连 的网络和个体观点的演化规则(即舆论演化模型). 接,并未考虑特殊节点对网络构建的影响.因此,这 本文在基于随机网络的社区和Deffuant模型的基础 些算法下构建的随机网络会出现一些孤立的节点和 上对网络舆论的演化过程进行了研究 一个节点只与其他社区存在边而与本社区不存在边 1.1基于随机网络的社区构建算法 的情况这导致构建的网络结构与真实环境下网民 Erdos和Renyi提出了随机网络的构建算法.该 关系网不符 算法规定山:初始设定N个孤立的节点,然后不断 针对上述问题,本文从真实网络的结构特点出 地在节点之间建立连接关系:每次随机加入1条边, 发,首先对随机网络模型进行改进,使其更加符合真 每条边以同样的概率p(0,其中V表 在随机网络的基础上,社区构建的方法为[: 示图G的顶点,V=[v2…w],E表示边, 单社区情况下,任意节点之间以概率P(0<P。< E=[e1e2.em].令n,=LI0NPm」,n2= 01)建立连接:在多社区构建上,社区内部任意节点 L5NPm」,n3=L10NP」.算法1和算法2分别给出 之间以内部连通概率Pm(0<Pm<0.1)建立连接,社 了单社区和多社区的随机网络构建算法
为丰富的舆论形态.司夏萌等[9] 将 Deffuant 模型应用 到多个社区上,仿真发现,除非社团间存在相反的观 点领袖,具有社团结构的 Deffuant 模型给出的最终舆 论形态取决于交互阈值,而与社团间的连通性无关. 虽然上述改进的 Deffuant 模型能够在一定程度上模 拟真实环境下网络舆论产生的过程,但受特定社区结 构的限制而不能在多个社区中通用,且存在个体交互 规则复杂、运算量大、考虑因素局限或构建的网络结 构与实际不符等缺陷. 此外,舆论是由无数个体的态度聚集在一起形 成的一个动态、整体的行为.从这个角度看,舆论亦 属于突现计算的研究范畴.突现计算[10] 是多个体系 统在处理复杂问题时所展现出来的一种思路逻辑, 它通过无数个简单行为过程的相互合作来形成更加 复杂的行为过程.姚远等[8] 从突现的角度对改进的 Deffuant 模型所描述的舆论行为进行了研究. 但其 仍然存在问题,即使用了复杂的不对称影响函数,使 得算法较复杂;模型仿真得到的各种舆论形态之间 的差别不够明显,影响对最终舆论趋势的判断;舆论 产生突现的时间较长,模型时间复杂度较大;没有考 虑个体的个性特征,不能解释群体中具有某些特性 的个体对最终舆论结果的影响. 针对上述问题,结合突现计算的思想,通过构建 比较符合实际的随机网络,本文在 Deffuant 模型的 基础上引入了意见领袖、易变个体和网民记忆 3 个 因素,建立了单、多社区通用的网络舆论突现计算模 型,并仿真分析了这些改进因素对网络舆论演化过 程以及最终舆论趋势的影响,以便为网络舆论研究 提供新的思路. 1 相关算法和模型 网络舆论演化与突现的 2 个要素是其赖以传播 的网络和个体观点的演化规则(即舆论演化模型). 本文在基于随机网络的社区和 Deffuant 模型的基础 上对网络舆论的演化过程进行了研究. 1.1 基于随机网络的社区构建算法 Erdös 和 Rényi 提出了随机网络的构建算法.该 算法规定[11] :初始设定 N 个孤立的节点,然后不断 地在节点之间建立连接关系;每次随机加入 1 条边, 每条边以同样的概率 p(0<p<1)从 C M [N(N-1) / 2] 条边 中随机选取. 在随机网络的基础上,社区构建的方法为[9] : 单社区情况下,任意节点之间以概率 Pin ( 0 <Pin < 0.1)建立连接;在多社区构建上,社区内部任意节点 之间以内部连通概率 Pin(0<Pin <0.1)建立连接,社 区之间任意节点之间以外部连通概率 Pout(0<Pout < Pin )建立连接.为了说明问题,这里将 2 个社区作为 多社区进行说明.在此社区构建方法中,每个节点以 等同的概率同其他节点建立连接.然而,在实际网络 环境中,受兴趣、爱好和个人魅力的影响,不同网民 所具有的连接数是不同的. 1.2 基于有限信任的 Deffuant 模型 在现实社会中,人们对某一问题的看法存在某 种程度的肯定或否定,并且人们偏向于同自己观点 相近的人进行交流.这种特点使 Deffuant 模型[5] 更 加符合真实社会环境中舆论的传播过程.该模型将 个体的观点值定义为[0,1]内的某一个随机值,每 次随机挑选 2 个个体 i 和 j 进行交互.在 t 时刻,如果 个体间观点 x 差的绝对值小于等于某一阈值 φ(即 | xi - xj | ≤ φ )则进行交互,否则不交互.在 t+1 时 刻,个体观点的变化如式(1): xi - xj ≤ φ 时, xi(t + 1) = xi(t) + ω × (xj(t) - xi(t)), xj(t + 1) = xj(t) + ω × (xi(t) - xj(t)); { xi - xj > φ 时, xi(t + 1) = xi(t), xj(t + 1) = xj(t). { (1) 式中:φ 表示个体间可进行交互的最大观点差值,ω 表示个体对交互者的信任程度. 2 随机网络构造算法的改进 网民之间的关系网络是根据网民的特性及喜好 建立,即考虑网民至少会与一个有较大影响力的网 民建立连接.真实网络社区特殊个体的存在,如意见 领袖,对网民关系网络的形成有很大影响.分析已有 的随机网络构建算法,发现其并未考虑上述因素,即 目前的随机网络以相等的概率建立节点之间的连 接,并未考虑特殊节点对网络构建的影响.因此,这 些算法下构建的随机网络会出现一些孤立的节点和 一个节点只与其他社区存在边而与本社区不存在边 的情况.这导致构建的网络结构与真实环境下网民 关系网不符. 针对上述问题,本文从真实网络的结构特点出 发,首先对随机网络模型进行改进,使其更加符合真 实情况. 构建的网络结构用表示, G = <V,E>,其中 V 表 示图 G 的顶点,V = v1 v2 ... v [ N ] ,E 表示边, E= e1 e2 ... e [ m ] . 令 n1 = ⌊ 10NPin 」, n2 = ⌊5NPin 」,n3 = ⌊ 10NPout」.算法 1 和算法 2 分别给出 了单社区和多社区的随机网络构建算法. ·544· 智 能 系 统 学 报 第 8 卷

第6期 吴渝,等:单、多社区通用的网络舆论突现计算模型 ·545. 算法1单社区随机网络构建算法, A=(A1,A2,,A:,,AN), 输入:N、Pm; A:={(:,s:,m:)|0≤:≤1,0≤s:≤1,0≤ 输出:G; m≤1,i=1,2,…,N}. 步骤: 式中:v:表示个体A,的观点值,s:表示A:对自己观 1)任意节点之间以概率P建立连接: 点的坚定程度:m:表示个体A:的记忆值:∫为个体i 2)意见领袖节点随机与n,个节点建立连接: 和j之间观点值的交互函数:P={p10p时,A:和A,观点变化都遵从: 的Deffuant模型的分析,发现存在以下问题:l)构建 (t+1)=,(t), (4) 的网民关系网络结构不合理:2)没有考虑网民的特 (m,(t+1)=m(t). 性:3)忽略了个体记忆对舆论演化过程的影响:4) 当|dg≤p时,A:和A观点变化都遵从: 忽略了舆论网络传播的跨社区性, :(t+1)=m:(t)-dg×(1-s:), (5) 基于不对称人际影响的舆论模型)、基于小世 m,(t+1)=(m,(t)+,(t))/2. 界网络的舆论模型[)】、具有社团结构的有界信任舆 式中:d为A和A:的观,点差值: 论涌现模型9)中,存在个体交互规则复杂,时间复 dg=:- (6) 杂度大,不能在多个社区通用的缺陷。 当交互双方一个为意见领袖而另一个为易变个 针对上述问题,本文在Deffuant模型的基础上, 体时,易变个体的观点值修改为意见领袖的观点值, 从突现计算的角度出发,引入意见领袖、易变个体和 此时意见领袖的观,点值不变.因为意见领袖有很强 个体记忆3个因素,合理修改了Deffuant模型的交 的说服力,而易变个体几乎没有主见,会完全信任意 互规则,来建立更加符合现实的交互规则的网络舆 见领袖:否则,当个体间的观点差值大于p时,个体 论模型,使其同时适用于单社区和多社区的环境, 间不进行交互,此时个体观点值和记忆值都不变,交 3.2单、多社区通用的网络舆论突现计算模型 互规则如式(4)所示:当个体间的观,点差值小于等 建模之前,先给出一些合理的假设.本文在沿用 于P时,个体进行交互,交互规则如式(5)所示. 姚远等模型假设[劉的基础上,再做进一步假设.由于 此外,个体的记忆按照式(7)变化: 真实的环境中某段时间内网络结构的变化是很微弱 m:(t)=(0.5)tw:(0)+(0.5)t-:(1)+…+ 的,因此网络结构的变化可以忽略故本文假设网络 (0.5)u.(t-1). (7) 结构在舆论传播的过程中不发生变化: 从式(7)可以看出,越早的观点对当前记忆的 本文模型将每个网民抽象成为一个个体,用S= 影响越小,从而对当前观点的影响也越小.当1很大 <A,P,f表示N个个体组成的系统其中, 时,初始的观点对当前记忆和观点的影响几乎为0
算法 1 单社区随机网络构建算法. 输入:N、Pin ; 输出:G; 步骤: 1) 任意节点之间以概率 Pin建立连接; 2) 意见领袖节点随机与 n1个节点建立连接; 3) 通过加边的方式,保证每一个节点都至少与 一个度数为 n2的节点有连接. 结束. 算法 2 多社区随机网络构建算法. 输入:N、Pin 、Pout; 输出:G; 步骤: 1) 非意见领袖节点以概率 Pin与内部节点建立 连接,以概率 Pout与外部节点建立连接; 2) 意见领袖节点随机与 n1个内部节点建立连 接,与 n3个外部节点建立连接; 3) 通过加边的方式,保证每一个节点都至少与 一个度数为 n2的内部节点有边. 结束. 3 单、多社区网络舆论突现计算模型 3.1 现有问题和本文思路 网民都有各自的个性特点,在交互过程中其观 点往往会受以前观点的影响.通过对当前各种改进 的 Deffuant 模型的分析,发现存在以下问题:1)构建 的网民关系网络结构不合理;2)没有考虑网民的特 性;3)忽略了个体记忆对舆论演化过程的影响;4) 忽略了舆论网络传播的跨社区性. 基于不对称人际影响的舆论模型[7] 、基于小世 界网络的舆论模型[8] 、具有社团结构的有界信任舆 论涌现模型[9] 中,存在个体交互规则复杂,时间复 杂度大,不能在多个社区通用的缺陷. 针对上述问题,本文在 Deffuant 模型的基础上, 从突现计算的角度出发,引入意见领袖、易变个体和 个体记忆 3 个因素,合理修改了 Deffuant 模型的交 互规则,来建立更加符合现实的交互规则的网络舆 论模型,使其同时适用于单社区和多社区的环境. 3.2 单、多社区通用的网络舆论突现计算模型 建模之前,先给出一些合理的假设.本文在沿用 姚远等模型假设[8]的基础上,再做进一步假设.由于 真实的环境中某段时间内网络结构的变化是很微弱 的,因此网络结构的变化可以忽略.故本文假设网络 结构在舆论传播的过程中不发生变化. 本文模型将每个网民抽象成为一个个体,用S = <A, P, f>表示 N 个个体组成的系统.其中, A = (A1 ,A2 ,...,Ai,...,AN) , Ai = {(vi,si,mi) | 0 ≤ vi ≤ 1, 0 ≤ si ≤ 1,0 ≤ mi ≤ 1, i = 1,2,…,N} . 式中:vi 表示个体 Ai 的观点值,si 表示 Ai 对自己观 点的坚定程度;mi 表示个体 Ai 的记忆值;f 为个体 i 和 j 之间观点值的交互函数;P = {φ| 0<φ<1}为系统 的参数集合,φ 为个体间进行交互的阈值,即个体间 进行交互的最大观点差值.在本文中,每个个体只与 其观点差值在交互阈值内的个体进行交互,否则不 交互. 假设个体 Ai 和 Aj 在 t 时刻的观点值分别为 vi(t)、vj(t),对自己观点的坚定程度值分别为 si、sj, 个体当前的记忆值分别为 mi(t)、mj(t),则根据交互 个体是否为意见领袖和易变个体,t+1 时刻 Ai 与 Aj 的观点交互规则由式(2) ~ (6)控制. 若 Ai 和 Aj,一个为意见领袖,另一个为易变个 体时(这里假定 Ai 为意见领袖),则 t+1 时刻 Ai 与 Aj 的观点值分别为: vi(t + 1) = vi(t), mi(t + 1) = mi(t). { (2) vj(t + 1) = vi(t), mj(t + 1) = (mj(t) + vj(t)) / 2. { (3) 除上述情况外,t+1 时刻个体间的交互规则为: 当 dij > φ 时,Ai 和 Aj 观点变化都遵从: vi(t + 1) = vi(t), {mi(t + 1) = mi(t). (4) 当 dij ≤ φ 时,Ai 和 Aj 观点变化都遵从: vi(t + 1) = mi(t) - dij × (1 - si), mi(t + 1) = (mi(t) + vi(t)) / 2. { (5) 式中:dij为 Ai 和 Aj 的观点差值: dij = vi - vj . (6) 当交互双方一个为意见领袖而另一个为易变个 体时,易变个体的观点值修改为意见领袖的观点值, 此时意见领袖的观点值不变.因为意见领袖有很强 的说服力,而易变个体几乎没有主见,会完全信任意 见领袖;否则,当个体间的观点差值大于 φ 时,个体 间不进行交互,此时个体观点值和记忆值都不变,交 互规则如式(4)所示;当个体间的观点差值小于等 于 φ 时,个体进行交互,交互规则如式(5)所示. 此外,个体的记忆按照式(7)变化: mi(t) = (0.5)tvi(0) + (0.5) t -vi(1) + … + (0.5)vi(t - 1). (7) 从式(7)可以看出,越早的观点对当前记忆的 影响越小,从而对当前观点的影响也越小.当 t 很大 时,初始的观点对当前记忆和观点的影响几乎为 0, 第 6 期 吴渝,等:单、多社区通用的网络舆论突现计算模型 ·545·

·546· 智能系统学报 第8卷 这与现实情况相符。 模型所揭示的舆论演化过程同基于不对称人际影响 3.3基于单、多社区通用的网络舆论模型的演化算 的舆论模型[)、基于小世界网络的舆论模型[8]和具 法描述 有社团结构的有界信任舆论涌现模型模型)所揭 单社区下的网络舆论演化模型以算法3给出. 示的舆论演化过程进行仿真对比分析. 初始时刻,意见领袖观点、易变个体观点、其他个体 4.1随机网络模型对比分析 观点的坚定程度分别为[0.8,1]、[0,0.2]和(0.2, 分别采用本文算法1和司夏萌等[9)的方法构 0.8)的随机值.在算法3中,初始化时个体容量为N, 建2个社区的随机网络,结果如图1所示.图1中, 个体间的交互次数为C,个体中意见领袖的比例为 Pn为0.02,P为0.0012,图1(a)中节点1~10与 L。,个体中易变个体的比例为巴。,个体间的交互阈值 51~60为意见领袖.从图1可以很明显看出本文方 为.首先根据3.2节算法1构建随机网络,根据个 法的结果更符合真实网络社区结构 体对事件的初始认识,随机给个体初始观点赋值,然 后个体之间按照既定的规则进行交互。 算法3单社区下网络舆论模型演化算法. 输入:N,C,lp,"p,P; 输出:C,D; 步骤: 1)根据输入初始化模型参数以及初始时刻所 (a)本文算法 (b)随机网络算法 有个体的观点值、坚定值和记忆值: 图1社区构建结果 2)对于个体A:,随机选择与其有边的个体A: Fig.I Results of community construction 3)判断2个体是否分别为意见领袖和易变个 4.2单社区下本文模型仿真结果及对比分析 体,是则根据式(2)~(3)计算个体进行交互后的 初始状态下,个体观点值:和个体观点坚定性s :(t+1)、m:(t+1)、(t+1)、m,(t+1),执行6): 均匀随机分布在[0,1]内.设定个体之间交互次数C= 4)根据式(6)计算d的值,确定其观点差异程度; 4O0.使用MATLAB对网络舆论的形成过程进行仿真. 5)根据式(4)~(5)计算个体进行交互后的 :(t+1)、m:(t+1)、y(t+1)、m(t+1): 表1单社区下参数设置 6)重复2)~5)直到遍历所有个体: Table 1 Parameter setting of single community 7)重复2)~6)直到满足外部终止条件 意见领袖 易变个体 交互阈值 结束 序号 比例(L。) 比例(。) (p) 在多社区情况下,这里以2个社区为例初始化 (a) 0.2 0.1 0.3 时,2个社区个体容量分别为N,、N,个体间交互次 (b) 0.2 0.3 0.3 数为C,个体中意见领袖的比例分别为,1,2,个体 (c) 0.2 0.5 0.3 中易变个体的比例分别为,12,个体间的交互阈 (d) 0.4 0.1 0.3 值为p.模型首先根据算法2构建随机网络,然后根 (e) 0.6 0.1 0.3 据个体对事件的初始认识,随机给个体初始意见赋 () 0.2 0.1 0.1 值,最后个体之间按照既定的规则进行交互因存在 (g) 0.2 0.1 0.5 (h) 0.0 0.0 多社区,考虑社区的非等同性,这里需要对2个社区 0.5 (i) 0.0 1.0 0.5 的个体数目、意见领袖的比例和易变个体的比例分 (Gj) 1.0 0.0 0.5 别输入,然后对2个社区分别初始化除输入与算法 3不同外,其他步骤与算法3相同,这里不再重复 在表1参数设置下,本文模型所揭示的舆论演 4模型仿真及对比分析 化过程如图2所示,其中图2中的标号同表1中的 序号相对应.由图2(a)、(b)、(c)可看出,在意见领 为了说明随机网络改进算法以及单、多社区通 袖和交互阈值相同的情况下,易变个体越多,舆论的 用的舆论模型的合理性和有效性,首先使用网络分 形成速度越慢.这主要是由于易变个体观点具有易 析工具Pajek进行网络构建,并与司夏萌等人多社 变性,时而支持,时而反对,导致与其交互的个体的 区随机网络构建模型进行对比:然后在MATLAB 2010b平台下,从单社区和多社区2个角度,将本文 观点值也随之上下跳动,使得舆论的形成速度变慢
这与现实情况相符. 3.3 基于单、多社区通用的网络舆论模型的演化算 法描述 单社区下的网络舆论演化模型以算法 3 给出. 初始时刻,意见领袖观点、易变个体观点、其他个体 观点的坚定程度分别为[0.8,1]、[0,0.2] 和(0.2, 0.8)的随机值.在算法 3 中,初始化时个体容量为 N, 个体间的交互次数为 C,个体中意见领袖的比例为 l p,个体中易变个体的比例为 vp,个体间的交互阈值 为 φ.首先根据 3.2 节算法 1 构建随机网络,根据个 体对事件的初始认识,随机给个体初始观点赋值,然 后个体之间按照既定的规则进行交互. 算法 3 单社区下网络舆论模型演化算法. 输入:N,C,l p,vp,φ; 输出:C,v; 步骤: 1) 根据输入初始化模型参数以及初始时刻所 有个体的观点值、坚定值和记忆值; 2) 对于个体 Ai,随机选择与其有边的个体 Aj; 3) 判断 2 个体是否分别为意见领袖和易变个 体,是则根据式(2) ~ (3) 计算个体进行交互后的 vi(t+1)、mi(t+1)、vj(t+1)、mj(t+1),执行 6); 4) 根据式(6)计算 dij的值,确定其观点差异程度; 5) 根据式(4) ~ (5) 计算个体进行交互后的 vi(t+1)、mi(t+1)、vj(t+1)、mj(t+1); 6) 重复 2) ~5)直到遍历所有个体; 7) 重复 2) ~6)直到满足外部终止条件. 结束. 在多社区情况下,这里以 2 个社区为例.初始化 时,2 个社区个体容量分别为 N1 、N2 ,个体间交互次 数为 C,个体中意见领袖的比例分别为 l p 1 、l p 2 ,个体 中易变个体的比例分别为 vp 1 、vp 2 ,个体间的交互阈 值为 φ.模型首先根据算法 2 构建随机网络,然后根 据个体对事件的初始认识,随机给个体初始意见赋 值,最后个体之间按照既定的规则进行交互.因存在 多社区,考虑社区的非等同性,这里需要对 2 个社区 的个体数目、意见领袖的比例和易变个体的比例分 别输入,然后对 2 个社区分别初始化.除输入与算法 3 不同外,其他步骤与算法 3 相同,这里不再重复. 4 模型仿真及对比分析 为了说明随机网络改进算法以及单、多社区通 用的舆论模型的合理性和有效性,首先使用网络分 析工具 Pajek 进行网络构建,并与司夏萌等人多社 区随机网络构建模型进行对比;然后在 MATLAB 2010b 平台下,从单社区和多社区 2 个角度,将本文 模型所揭示的舆论演化过程同基于不对称人际影响 的舆论模型[7] 、基于小世界网络的舆论模型[8] 和具 有社团结构的有界信任舆论涌现模型模型[9] 所揭 示的舆论演化过程进行仿真对比分析. 4.1 随机网络模型对比分析 分别采用本文算法 1 和司夏萌等[9] 的方法构 建 2 个社区的随机网络,结果如图 1 所示.图 1 中, Pin为 0.02,Pout为 0.001 2,图 1( a)中节点 1 ~ 10 与 51~60 为意见领袖.从图 1 可以很明显看出本文方 法的结果更符合真实网络社区结构. (a) 本文算法 (b)随机网络算法 图 1 社区构建结果 Fig.1 Results of community construction 4.2 单社区下本文模型仿真结果及对比分析 初始状态下,个体观点值 v 和个体观点坚定性 s 均匀随机分布在[0,1]内.设定个体之间交互次数 C = 400.使用 MATLAB 对网络舆论的形成过程进行仿真. 表 1 单社区下参数设置 Table 1 Parameter setting of single community 序号 意见领袖 比例( l p ) 易变个体 比例( vp ) 交互阈值 ( φ ) (a) 0.2 0.1 0.3 (b) 0.2 0.3 0.3 (c) 0.2 0.5 0.3 (d) 0.4 0.1 0.3 (e) 0.6 0.1 0.3 (f) 0.2 0.1 0.1 (g) 0.2 0.1 0.5 (h) 0.0 0.0 0.5 (i) 0.0 1.0 0.5 (j) 1.0 0.0 0.5 在表 1 参数设置下,本文模型所揭示的舆论演 化过程如图 2 所示,其中图 2 中的标号同表 1 中的 序号相对应.由图 2(a)、(b)、(c)可看出,在意见领 袖和交互阈值相同的情况下,易变个体越多,舆论的 形成速度越慢.这主要是由于易变个体观点具有易 变性,时而支持,时而反对,导致与其交互的个体的 观点值也随之上下跳动,使得舆论的形成速度变慢. ·546· 智 能 系 统 学 报 第 8 卷
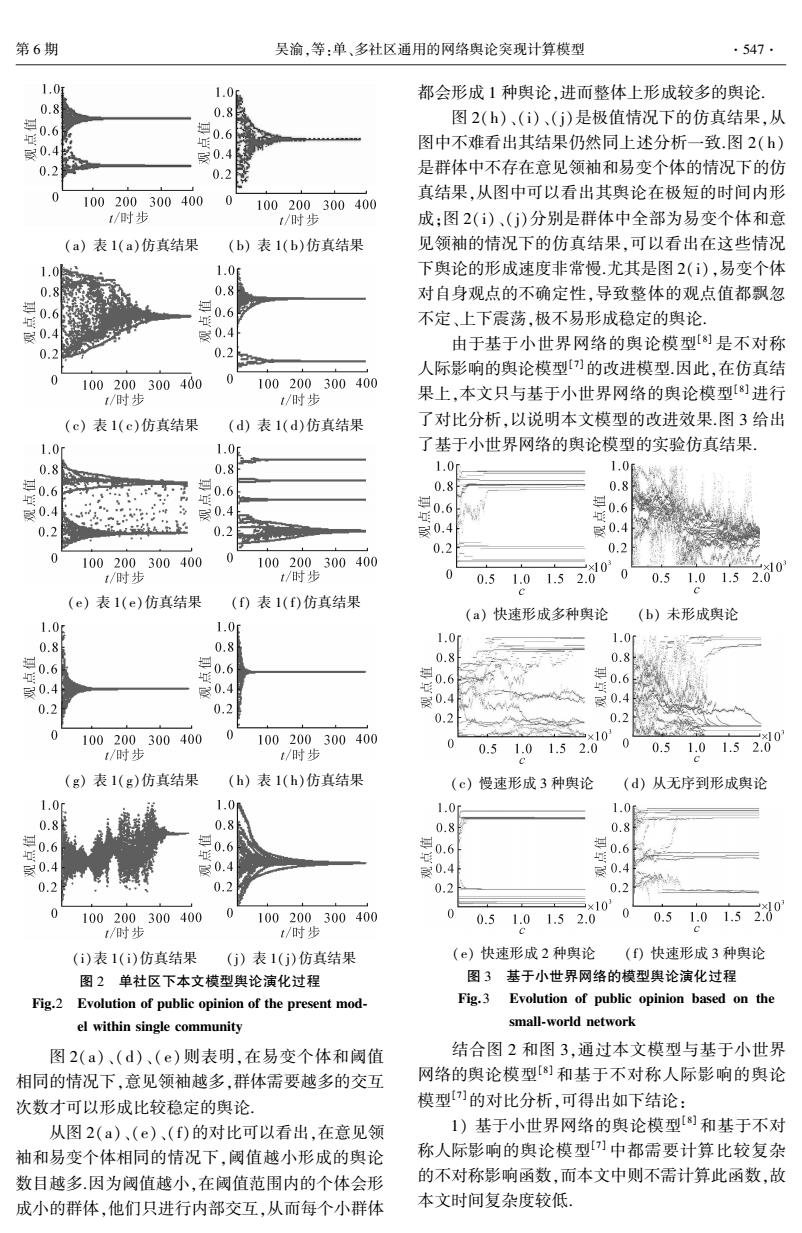
第6期 吴渝,等:单、多社区通用的网络舆论突现计算模型 .547. 1.0厘 1.0 都会形成1种舆论,进而整体上形成较多的舆论, 0.8 0.8 图2(h)、(i)、(Gj)是极值情况下的仿真结果,从 0.6 0.6 厨0.4 图中不难看出其结果仍然同上述分析一致.图2(h) 假 0.4 0.2 0.2 是群体中不存在意见领袖和易变个体的情况下的仿 真结果,从图中可以看出其舆论在极短的时间内形 100200300400 100200300400 1/时步 t/时步 成;图2()、(j)分别是群体中全部为易变个体和意 (a)表1(a)仿真结果 (b)表1(b)仿真结果 见领袖的情况下的仿真结果,可以看出在这些情况 1.0 1.0g 下舆论的形成速度非常慢.尤其是图2(),易变个体 0.8 0.8 对自身观点的不确定性,导致整体的观点值都飘忽 0.6 0.6 不定、上下震荡,极不易形成稳定的舆论。 0.4 0.4 由于基于小世界网络的奥论模型[劉是不对称 0.2 0.2 人际影响的舆论模型)的改进模型因此,在仿真结 0 100200300400 0 100200300400 t/时步 t/时步 果上,本文只与基于小世界网络的舆论模型劉进行 (c)表1(c)仿真结果 (d)表1(d)仿真结果 了对比分析,以说明本文模型的改进效果.图3给出 1.0r 1.0p 了基于小世界网络的舆论模型的实验仿真结果 0.8 0.8 1.0 1.0 0.6 0.6 0.8 0.8 30.4 0.4 是06 0.6 啦 0.2 0.2 受0.4 0.4; 0.2 0.2 0 100200300400 0 100200300400 ×103 0 1/时步 t/时步 0 0.5 1.01.52.0 0 0.51.01.52.0 (e)表1(e)仿真结果 (f)表1(f)仿真结果 (a)快速形成多种舆论 (b)未形成舆论 1.0g 1.0g 1.0r 1.0r 0.8 0.8 0.6 0.8 0.8 0.6 0.6 坦 0.6 0.4 厨0.4 0.2 0.2 30.4 0.4 0.2 0.2 100200300400 0 100200300400 当×103 0 0 0 t/时步 t/时步 0.5 1.0 1.52.0 0.5 1.01.52.0 (g)表1(g)仿真结果 (h)表1(h)仿真结果 (c)慢速形成3种舆论 (d)从无序到形成舆论 1.0r 1.0 1.0r 1.0 0.8 0.8 0.8 0.8 0.6 0.6 逗0.6 过0.6 0.4 0.4 0.4 0.4 0.2 0.2 0.2 0.2 三×103 0 100200300400 0 100200300400 0.5 1.0 1.52.0 0 0.5 01.5280 t/时步 t/时步 (i)表1(i)仿真结果 (j)表1(Gj)仿真结果 (e)快速形成2种舆论 ()快速形成3种舆论 图2单社区下本文模型舆论演化过程 图3基于小世界网络的模型舆论演化过程 Fig.2 Evolution of public opinion of the present mod- Fig.3 Evolution of public opinion based on the el within single community small-world network 图2(a)、(d)、(e)则表明,在易变个体和阈值 结合图2和图3,通过本文模型与基于小世界 相同的情况下,意见领袖越多,群体需要越多的交互 网络的舆论模型[]和基于不对称人际影响的舆论 次数才可以形成比较稳定的舆论 模型的对比分析,可得出如下结论: 从图2(a)、(e)、(f)的对比可以看出,在意见领 1)基于小世界网络的舆论模型劉和基于不对 袖和易变个体相同的情况下,阈值越小形成的奥论 称人际影响的舆论模型[]中都需要计算比较复杂 数目越多因为阈值越小,在阈值范围内的个体会形 的不对称影响函数,而本文中则不需计算此函数,故 成小的群体,他们只进行内部交互,从而每个小群体 本文时间复杂度较低
(a) 表 1(a)仿真结果 (b) 表 1(b)仿真结果 (c) 表 1(c)仿真结果 (d) 表 1(d)仿真结果 (e) 表 1(e)仿真结果 (f) 表 1(f)仿真结果 (g) 表 1(g)仿真结果 (h) 表 1(h)仿真结果 (i)表 1(i)仿真结果 (j) 表 1(j)仿真结果 图 2 单社区下本文模型舆论演化过程 Fig.2 Evolution of public opinion of the present mod⁃ el within single community 图 2(a)、( d)、( e)则表明,在易变个体和阈值 相同的情况下,意见领袖越多,群体需要越多的交互 次数才可以形成比较稳定的舆论. 从图 2(a)、(e)、(f)的对比可以看出,在意见领 袖和易变个体相同的情况下,阈值越小形成的舆论 数目越多.因为阈值越小,在阈值范围内的个体会形 成小的群体,他们只进行内部交互,从而每个小群体 都会形成 1 种舆论,进而整体上形成较多的舆论. 图 2(h)、(i)、(j)是极值情况下的仿真结果,从 图中不难看出其结果仍然同上述分析一致.图 2(h) 是群体中不存在意见领袖和易变个体的情况下的仿 真结果,从图中可以看出其舆论在极短的时间内形 成;图 2(i)、(j)分别是群体中全部为易变个体和意 见领袖的情况下的仿真结果,可以看出在这些情况 下舆论的形成速度非常慢.尤其是图 2(i),易变个体 对自身观点的不确定性,导致整体的观点值都飘忽 不定、上下震荡,极不易形成稳定的舆论. 由于基于小世界网络的舆论模型[8] 是不对称 人际影响的舆论模型[7]的改进模型.因此,在仿真结 果上,本文只与基于小世界网络的舆论模型[8] 进行 了对比分析,以说明本文模型的改进效果.图 3 给出 了基于小世界网络的舆论模型的实验仿真结果. (a) 快速形成多种舆论 (b) 未形成舆论 (c) 慢速形成 3 种舆论 (d) 从无序到形成舆论 (e) 快速形成 2 种舆论 (f) 快速形成 3 种舆论 图 3 基于小世界网络的模型舆论演化过程 Fig.3 Evolution of public opinion based on the small⁃world network 结合图 2 和图 3,通过本文模型与基于小世界 网络的舆论模型[8] 和基于不对称人际影响的舆论 模型[7]的对比分析,可得出如下结论: 1) 基于小世界网络的舆论模型[8] 和基于不对 称人际影响的舆论模型[7] 中都需要计算比较复杂 的不对称影响函数,而本文中则不需计算此函数,故 本文时间复杂度较低. 第 6 期 吴渝,等:单、多社区通用的网络舆论突现计算模型 ·547·
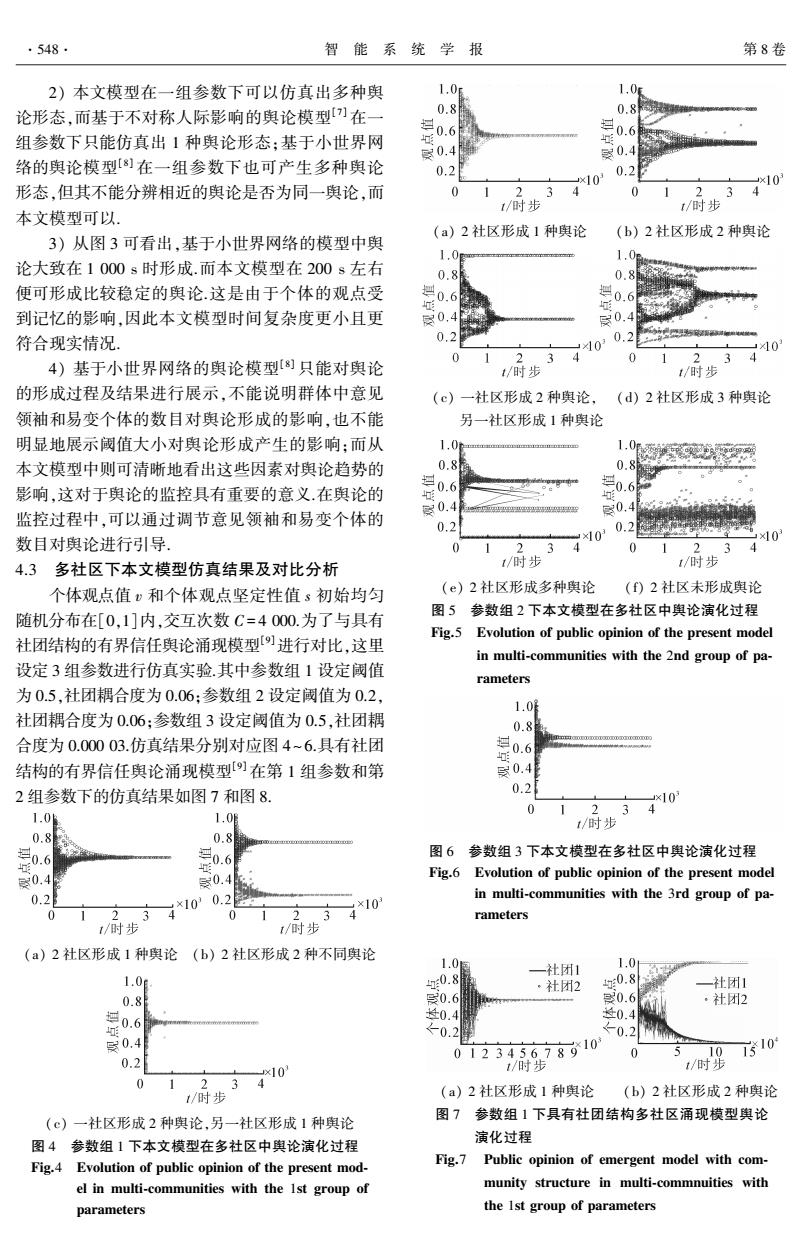
.548 智能系统学报 第8卷 2)本文模型在一组参数下可以仿真出多种舆 1.0 论形态,而基于不对称人际影响的舆论模型刀在一 0.8 0.8好 0.6 0.6 组参数下只能仿真出1种舆论形态:基于小世界网 厨0.4 0.4 络的舆论模型[劉在一组参数下也可产生多种舆论 0.2 0.2 x10 x10 形态,但其不能分辨相近的舆论是否为同一舆论,而 1 234 1/时步 t/时步 本文模型可以: (a)2社区形成1种舆论 (b)2社区形成2种舆论 3)从图3可看出,基于小世界网络的模型中舆 1.0 1.0 论大致在1000s时形成.而本文模型在200s左右 0.8 0.8 便可形成比较稳定的舆论.这是由于个体的观点受 0.6 0.0 到记忆的影响,因此本文模型时间复杂度更小且更 0, 0. 符合现实情况. 0.2 103 40 0 2 3 4 4)基于小世界网络的舆论模型[幻只能对舆论 0 1 234 t/时步 t/时步 的形成过程及结果进行展示,不能说明群体中意见 (c)一社区形成2种舆论,(d)2社区形成3种舆论 领袖和易变个体的数目对舆论形成的影响,也不能 另一社区形成1种舆论 明显地展示阈值大小对舆论形成产生的影响:而从 1.0 1.02 本文模型中则可清晰地看出这些因素对舆论趋势的 0.8 0.8 影响,这对于舆论的监控具有重要的意义.在舆论的 20.6 0.6 0.4 带 0.489“ 监控过程中,可以通过调节意见领袖和易变个体的 0.2 0.2 数目对舆论进行引导. ×刘03 ×10 0 2 34 0 1234 4.3多社区下本文模型仿真结果及对比分析 1/时步 t/时步 个体观点值)和个体观点坚定性值s初始均匀 (e)2社区形成多种舆论 ()2社区未形成舆论 随机分布在[0,1]内,交互次数C=4000.为了与具有 图5参数组2下本文模型在多社区中舆论演化过程 Fig.5 Evolution of public opinion of the present model 社团结构的有界信任奥论涌现模型进行对比,这里 in multi-communities with the 2nd group of pa- 设定3组参数进行仿真实验.其中参数组1设定阈值 rameters 为0.5,社团耦合度为0.06:参数组2设定阈值为0.2, 1.0 社团耦合度为0.06:参数组3设定阈值为0.5,社团耦 0.8 合度为0.00003.仿真结果分别对应图4~6.具有社团 已0.6 结构的有界信任奥论涌现模型)在第1组参数和第 0.4 2组参数下的仿真结果如图7和图8. 0.2 ×10 0 1 1.0 1.06 2.34 t/时步 0.8 0.8 20.6 三0.6 图6参数组3下本文模型在多社区中舆论演化过程 04 0.4 Fig.6 Evolution of public opinion of the present model 0.2 ×1030.2 in multi-communities with the 3rd group of pa- ×10 0 1234 0 1 23 4 rameters 1/时步 t/时步 (a)2社区形成1种舆论(b)2社区形成2种不同舆论 1.0 一社团1 1.0 1.0e 0.8 ·社团2 0.8 一社团1 0.8 0.6 0.6 ·社团2 0.4 检0.4 0,4 0.2 0.2 0 10 1510 0.2 012345678910 10 1/时步 t/时步 0 234 1/时步 (a)2社区形成1种舆论 (b)2社区形成2种舆论 (©)一社区形成2种舆论,另一社区形成1种舆论 图7参数组1下具有社团结构多社区涌现模型舆论 图4参数组1下本文模型在多社区中舆论演化过程 演化过程 Fig.4 Evolution of public opinion of the present mod- Fig.7 Public opinion of emergent model with com- el in multi-communities with the Ist group of munity structure in multi-commnuities with parameters the Ist group of parameters
2) 本文模型在一组参数下可以仿真出多种舆 论形态,而基于不对称人际影响的舆论模型[7] 在一 组参数下只能仿真出 1 种舆论形态;基于小世界网 络的舆论模型[8] 在一组参数下也可产生多种舆论 形态,但其不能分辨相近的舆论是否为同一舆论,而 本文模型可以. 3) 从图 3 可看出,基于小世界网络的模型中舆 论大致在 1 000 s 时形成.而本文模型在 200 s 左右 便可形成比较稳定的舆论.这是由于个体的观点受 到记忆的影响,因此本文模型时间复杂度更小且更 符合现实情况. 4) 基于小世界网络的舆论模型[8] 只能对舆论 的形成过程及结果进行展示,不能说明群体中意见 领袖和易变个体的数目对舆论形成的影响,也不能 明显地展示阈值大小对舆论形成产生的影响;而从 本文模型中则可清晰地看出这些因素对舆论趋势的 影响,这对于舆论的监控具有重要的意义.在舆论的 监控过程中,可以通过调节意见领袖和易变个体的 数目对舆论进行引导. 4.3 多社区下本文模型仿真结果及对比分析 个体观点值 v 和个体观点坚定性值 s 初始均匀 随机分布在[0,1]内,交互次数 C = 4 000.为了与具有 社团结构的有界信任舆论涌现模型[9]进行对比,这里 设定 3 组参数进行仿真实验.其中参数组 1 设定阈值 为 0.5,社团耦合度为 0.06;参数组 2 设定阈值为 0.2, 社团耦合度为 0.06;参数组 3 设定阈值为 0.5,社团耦 合度为 0.000 03.仿真结果分别对应图 4~6.具有社团 结构的有界信任舆论涌现模型[9] 在第 1 组参数和第 2 组参数下的仿真结果如图 7 和图 8. (a) 2 社区形成 1 种舆论 (b) 2 社区形成 2 种不同舆论 (c) 一社区形成 2 种舆论,另一社区形成 1 种舆论 图 4 参数组 1 下本文模型在多社区中舆论演化过程 Fig.4 Evolution of public opinion of the present mod⁃ el in multi⁃communities with the 1st group of parameters (a) 2 社区形成 1 种舆论 (b) 2 社区形成 2 种舆论 (c) 一社区形成 2 种舆论, (d) 2 社区形成 3 种舆论 另一社区形成 1 种舆论 (e) 2 社区形成多种舆论 (f) 2 社区未形成舆论 图 5 参数组 2 下本文模型在多社区中舆论演化过程 Fig.5 Evolution of public opinion of the present model in multi⁃communities with the 2nd group of pa⁃ rameters 图 6 参数组 3 下本文模型在多社区中舆论演化过程 Fig.6 Evolution of public opinion of the present model in multi⁃communities with the 3rd group of pa⁃ rameters (a) 2 社区形成 1 种舆论 (b) 2 社区形成 2 种舆论 图 7 参数组 1 下具有社团结构多社区涌现模型舆论 演化过程 Fig.7 Public opinion of emergent model with com⁃ munity structure in multi⁃commnuities with the 1st group of parameters ·548· 智 能 系 统 学 报 第 8 卷

第6期 吴渝,等:单、多社区通用的网络舆论突现计算摸型 ·549. 1.0 有网民进行社区划分:3)使用PageRank算法[),获 0.8 一社团1 30.6 一社团1·社团2 取每个社区的意见领袖:4)提取2011年3月11日 这0.4 。社团2 检0.4 至2011年12月31日所有有关日本地震的帖子及 ←0.2 ←0.2 回复信息:5)提取所有参与该事件的网民关系网 0 1 234 10 0 1234510 t/时步 1/时步 络:6)人工分析每个网民发表的信息,辨别易变个 (a)2社区形成2种舆论(b)2社区形成3种舆论 体、观点值及每个网民的观点坚定程度值. 图8参数组2下具有社团结构多社区涌现模型舆论 将3月11日的相关数据作为初始数据,对本文 演化过程 模型下舆论的演化过程进行仿真,并与真实结果进 Fig.8 Evolution of public opinion of emergent model 行对比. with community structure in multi-commnu- 2011年3月11日至2011年年底网民共发帖 ities with the 2nd group of parameters 301条,11日当天共发帖47条,参与讨论15727人 图4~6和图7~8的对比表明,与具有社团结构 次,参与者大致被分为2个社区.11日当天,92.5% 的有界信任舆论涌现模型[)相比,本文模型能够展 的网民对日本地震事件感到兴奋,4.3%的网民感到 现更加丰富的舆论形态, 同情,3.2%的网民感到与自己无关在观点交换的过 图4(a)中舆论的突现时间大约在2000s左 程中,网民对同情者进行了严厉的批评,导致越来越 右,而图7(a)中奥论突现的时间大约在2500s左 少的人敢于表现同情,逐渐形成一种对日本地震感 右这说明本文模型舆论形成的速度更快,时间复杂 到兴奋的舆论, 度更低。 用本文模型进行仿真,用个体观点值0表示绝 图4(a)图与图6对比说明了社区耦合度对舆 对同情,1表示绝对兴奋,中间值表示趋于同情与兴 论的影响.图6中2个社区形成2种不同的舆论趋 奋之间的某一感情,结果如图9所示.仿真结果表 势,但这2种舆论的差值在阈值的范围内.这主要是 明,初始时刻多数网民对日本地震话题持兴奋感情, 因为社区耦合度太小,导致了社区之间的联系几乎 到500s时,观点已经基本稳定,网民整体趋于兴奋 为零,从而使得2个社区没有形成统一的观点.这与 感情,少数网民仍旧感到同情 司夏萌得出的社团连通性差时社团间观点对立,社 1.0m 团连通性好时社团间观点统一的结论大致相符】 0.8 图4(a)与图7(b)对比说明了意见领袖对舆论 0.6 的影响这2个图都设有意见领袖,但是最终舆论走 0.4 向却不同.从图7(b)可明显看出,社区整体态度完 0.2m-… x10 0 1234 全由意见领袖所决定,这与实际情况不符,因为意见 t/时步 领袖也会受到社区内其他个体的影响,不可能对其 图9日本地震舆论传播仿真结果 他个体观点无动于衷而本文模型中,舆论的形成不 Fig.9 Simulation result of the public opinion about 完全受制于意见领袖,而是由整个群体所决定, earthquake in Japan 4.4真实数据下本文模型仿真结果 上述分析仿真对比说明,本文建立的模型能够 为说明本文模型的实用性,本文在真实数据下 重现多社区网络舆论演化过程,同时验证了本文模 将本文模型的奥论演化过程和实际舆论的演化过程 型的正确性和可用性。 进行了对比分析.由于现实中网络群体存在着异样 由于基于小世界网络的舆论模型)没有考虑群 性,即具有相同喜好的人会形成一个社区,具有不同 体的异样性,因此在该事件中并未与其进行对比分 喜好的人会分布于不同的社区因此对网络舆论事 析.具有社团结构的有界信任舆论涌现模型)网络舆 件的研究就必须要考虑该因素,即在进行舆论研究 论形成的结果完全由意见领袖所决定因此,在该事 之前就必须先对参与者进行社区划分.本文从该角 件中该模型会形成极化的舆论形态,即要么绝对兴 度对本文提出的单、多社区通用的网络舆论突现计 奋,要么绝对同情,其结果与事实不符.而本文算法简 算模型进行验证.因真实数据无法采集单社区数据, 单,模型仿真速度更快,性能更好,且仿真结果较具有 本文以2011年3月11日“日本地震事件”为例进行 社团结构的有界信任舆论涌现模型⑨)更合理。 说明步骤如下:1)运用爬虫程序抓取天涯论坛所 有帖子及回复信息,建立带权重的关系网络:2)运 5 结束语 用秦晓等提出的社区划分算法[]对天涯论坛的所 本文给出了较符合现实的随机网络模型构建算
(a) 2 社区形成 2 种舆论 (b) 2 社区形成 3 种舆论 图 8 参数组 2 下具有社团结构多社区涌现模型舆论 演化过程 Fig.8 Evolution of public opinion of emergent model with community structure in multi⁃commnu⁃ ities with the 2nd group of parameters 图 4~6 和图 7~8 的对比表明,与具有社团结构 的有界信任舆论涌现模型[9] 相比,本文模型能够展 现更加丰富的舆论形态. 图 4( a) 中舆论的突现时间大约在 2 000 s 左 右,而图 7(a)中舆论突现的时间大约在 2 500 s 左 右.这说明本文模型舆论形成的速度更快,时间复杂 度更低. 图 4(a)图与图 6 对比说明了社区耦合度对舆 论的影响.图 6 中 2 个社区形成 2 种不同的舆论趋 势,但这 2 种舆论的差值在阈值的范围内.这主要是 因为社区耦合度太小,导致了社区之间的联系几乎 为零,从而使得 2 个社区没有形成统一的观点.这与 司夏萌得出的社团连通性差时社团间观点对立,社 团连通性好时社团间观点统一的结论大致相符. 图 4(a)与图 7(b)对比说明了意见领袖对舆论 的影响.这 2 个图都设有意见领袖,但是最终舆论走 向却不同.从图 7( b)可明显看出,社区整体态度完 全由意见领袖所决定,这与实际情况不符,因为意见 领袖也会受到社区内其他个体的影响,不可能对其 他个体观点无动于衷.而本文模型中,舆论的形成不 完全受制于意见领袖,而是由整个群体所决定. 4.4 真实数据下本文模型仿真结果 为说明本文模型的实用性,本文在真实数据下 将本文模型的舆论演化过程和实际舆论的演化过程 进行了对比分析.由于现实中网络群体存在着异样 性,即具有相同喜好的人会形成一个社区,具有不同 喜好的人会分布于不同的社区.因此对网络舆论事 件的研究就必须要考虑该因素,即在进行舆论研究 之前就必须先对参与者进行社区划分.本文从该角 度对本文提出的单、多社区通用的网络舆论突现计 算模型进行验证.因真实数据无法采集单社区数据, 本文以 2011 年 3 月 11 日“日本地震事件”为例进行 说明.步骤如下:1) 运用爬虫程序抓取天涯论坛所 有帖子及回复信息,建立带权重的关系网络;2) 运 用秦晓等提出的社区划分算法[12] 对天涯论坛的所 有网民进行社区划分;3)使用 PageRank 算法[13] ,获 取每个社区的意见领袖;4) 提取 2011 年 3 月 11 日 至 2011 年 12 月 31 日所有有关日本地震的帖子及 回复信息;5) 提取所有参与该事件的网民关系网 络;6) 人工分析每个网民发表的信息,辨别易变个 体、观点值及每个网民的观点坚定程度值. 将 3 月 11 日的相关数据作为初始数据,对本文 模型下舆论的演化过程进行仿真,并与真实结果进 行对比. 2011 年 3 月 11 日至 2011 年年底网民共发帖 301 条,11 日当天共发帖 47 条,参与讨论 15 727 人 次,参与者大致被分为 2 个社区.11 日当天,92.5% 的网民对日本地震事件感到兴奋,4.3%的网民感到 同情,3.2%的网民感到与自己无关.在观点交换的过 程中,网民对同情者进行了严厉的批评,导致越来越 少的人敢于表现同情,逐渐形成一种对日本地震感 到兴奋的舆论. 用本文模型进行仿真,用个体观点值 0 表示绝 对同情,1 表示绝对兴奋,中间值表示趋于同情与兴 奋之间的某一感情,结果如图 9 所示.仿真结果表 明,初始时刻多数网民对日本地震话题持兴奋感情, 到 500 s 时,观点已经基本稳定,网民整体趋于兴奋 感情,少数网民仍旧感到同情. 图 9 日本地震舆论传播仿真结果 Fig. 9 Simulation result of the public opinion about earthquake in Japan 上述分析仿真对比说明,本文建立的模型能够 重现多社区网络舆论演化过程,同时验证了本文模 型的正确性和可用性. 由于基于小世界网络的舆论模型[8] 没有考虑群 体的异样性,因此在该事件中并未与其进行对比分 析.具有社团结构的有界信任舆论涌现模型[9]网络舆 论形成的结果完全由意见领袖所决定.因此,在该事 件中该模型会形成极化的舆论形态,即要么绝对兴 奋,要么绝对同情,其结果与事实不符.而本文算法简 单,模型仿真速度更快,性能更好,且仿真结果较具有 社团结构的有界信任舆论涌现模型[9]更合理. 5 结束语 本文给出了较符合现实的随机网络模型构建算 第 6 期 吴渝,等:单、多社区通用的网络舆论突现计算模型 ·549·

.550. 智能系统学报 第8卷 法,并提出了单、多社区通用的网络舆论模型仿真数 8]WU Yu,YAO Yuan,WANG Li.A novel emergence model 据下的实验结果表明,本文构建的随机网络结果更符 of public opinion based on small-world network[J].Journal 合现实,算法时间复杂度较小,仿真结果更加丰富,能 of Key Engineering Materials,2011,474-476:2263-2268. 够重现网络事件的传播过程.本文工作表明,社区中 [9]司夏萌,刘云,丁飞,等.具有社团结构的有界信任舆 论涌现模型研究[J].系统仿真学报,2009,23(7): 意见领袖的数目、易变个体的数目会影响舆论形成的 7644-7647. 时间、阈值,外部连通概率会影响舆论形成的时间和 SI Xiameng,LIU Yun,DING Fei,et al.Research on 数目但是,本文模型未考虑网络群体的异样性以及 bounded confidence consensus emergency model with com- 意见领袖和易变个体的识别方法.由于当前对网络奥 munity structureJ.Journal of System Simulation,2009, 论的研究都集中在模型的应用上,本文也未从理论上 23(7):7644-7647. 对模型进行验证,这将是今后工作的重点 [10]吴渝,唐红,刘洪涛.网络群体智能与突现计算[M] 北京:科学出版社,2012:1-320. 参考文献: [11]NEWMAN M E J.The structure and function of complex networks[J].SIAM Review,2003,45(2):167-256. [1]SZNAJD-WERON K,JOZEF S.Opinion evolution in closed 12]LIU Hongtao,QIN Xiao,YUN Hongfeng,et al.A commu- community [J.International Journal of Modern Physics C, nity detecting algorithm in directed weighted networksJ 2000,11(6):1157-1165 Lecture Notes in Electrical Engineering,2011,2:11-17. [2]S0OD V,REDNER S.Voter model on heterogeneous graphs [13]肖宇,许炜,夏霖.网络社区中的意见领袖特征分析 [J].Physical Review Letters,2005,94:178701. [J].计算机工程与科学,2011(33):150-156. [3]GALAMA S.Minority opinion spreading in random geometry XIAO Yu,XU Wei,XIA Lin.A feature analysis of the o- [J].The European Physical Joumal B,2002,25(4): pinion leader in on-line communities[J].Computer Engi- 403-406. neering and Science,2011(33):150-156. [4]LAKOWSKI KK,NAWOJCZYK M.The galam model of 作者简介: minority opinion spreading and the marriage gap[J].Inter- 吴渝,女,1970年生,教授,博士生 national Journal of Modern Physics C,2008,19(4):611- 导师,主要研究方向为网络智能、数字 615. 媒体技术等获省部级科技奖2项,出版 [5]DEFFUANT G,NEAU D,AMBLARD F,et al.Mixing be- 著作3部,发表学术论文100余篇 liefs among interacting agents[J].Advances in Complex Systems,2000,3(1/2/3/4):87-98. [6]HEGSELMANN R,KRAUSE U.Dynamics and bounded 李强,男,1987年生,硕士研究生, confidence models,analysis and simulation[].Journal of 主要研究方向为网络智能. Artificial Societies and Social Simulation,2002,5(3):2. [7]刘常昱,胡晓峰,罗批,等.基于不对称人际影响的舆 论现模型研究[J].系统仿真学报,2008,20(4):990- 996. LIU Changyu,HU Xiaofeng,LUO Pi,et al.Study on con- 刘洪涛,男,1974年生,副教授,硕 sensus emergency model based on asymmetric personal rela- 士生导师,主要研究方向为社会计算、 tionship influence[J].Journal of System Simulation,2008, 群体智能和网络舆情,发表学术论文10 20(4):990-996. 余篇
法,并提出了单、多社区通用的网络舆论模型.仿真数 据下的实验结果表明,本文构建的随机网络结果更符 合现实,算法时间复杂度较小,仿真结果更加丰富,能 够重现网络事件的传播过程.本文工作表明,社区中 意见领袖的数目、易变个体的数目会影响舆论形成的 时间、阈值,外部连通概率会影响舆论形成的时间和 数目.但是,本文模型未考虑网络群体的异样性以及 意见领袖和易变个体的识别方法.由于当前对网络舆 论的研究都集中在模型的应用上,本文也未从理论上 对模型进行验证,这将是今后工作的重点. 参考文献: [1]SZNAJD⁃WERON K, JOZEF S. Opinion evolution in closed community [J]. International Journal of Modern Physics C , 2000, 11(6): 1157⁃1165. [2]SOOD V, REDNER S. Voter model on heterogeneous graphs [J]. Physical Review Letters , 2005, 94:178701. [3]GALAMA S. Minority opinion spreading in random geometry [J]. The European Physical Journal B , 2002, 25 ( 4): 403⁃406. [ 4] LAKOWSKI K K, NAWOJCZYK M. The galam model of minority opinion spreading and the marriage gap[J]. Inter⁃ national Journal of Modern Physics C , 2008, 19(4): 611⁃ 615. [5]DEFFUANT G, NEAU D, AMBLARD F, et al. Mixing be⁃ liefs among interacting agents [ J]. Advances in Complex Systems , 2000, 3(1 / 2 / 3 / 4): 87⁃98. [6] HEGSELMANN R, KRAUSE U. Dynamics and bounded confidence models, analysis and simulation[ J]. Journal of Artificial Societies and Social Simulation , 2002, 5(3): 2. [7]刘常昱, 胡晓峰, 罗批, 等. 基于不对称人际影响的舆 论涌现模型研究[J]. 系统仿真学报, 2008, 20(4): 990⁃ 996. LIU Changyu, HU Xiaofeng, LUO Pi, et al. Study on con⁃ sensus emergency model based on asymmetric personal rela⁃ tionship influence[J]. Journal of System Simulation, 2008, 20(4): 990⁃996. [8]WU Yu, YAO Yuan, WANG Li. A novel emergence model of public opinion based on small⁃world network[ J]. Journal of Key Engineering Materials, 2011, 474⁃476: 2263⁃2268. [9]司夏萌, 刘云, 丁飞, 等. 具有社团结构的有界信任舆 论涌现模型研究[ J]. 系统仿真学报, 2009, 23 ( 7): 7644⁃7647. SI Xiameng, LIU Yun, DING Fei, et al. Research on bounded confidence consensus emergency model with com⁃ munity structure[ J]. Journal of System Simulation, 2009, 23(7): 7644⁃7647. [10]吴渝, 唐红, 刘洪涛. 网络群体智能与突现计算[M]. 北京:科学出版社, 2012: 1⁃320. [11]NEWMAN M E J. The structure and function of complex networks[J]. SIAM Review, 2003, 45(2): 167⁃256. [12]LIU Hongtao, QIN Xiao, YUN Hongfeng, et al. A commu⁃ nity detecting algorithm in directed weighted networks[ J]. Lecture Notes in Electrical Engineering, 2011, 2: 11⁃17. [13]肖宇, 许炜, 夏霖.网络社区中的意见领袖特征分析 [J].计算机工程与科学, 2011(33): 150⁃156. XIAO Yu, XU Wei, XIA Lin. A feature analysis of the o⁃ pinion leader in on⁃line communities[ J]. Computer Engi⁃ neering and Science, 2011(33): 150⁃156. 作者简介: 吴渝,女,1970 年生,教授,博士生 导师,主要研究方向为网络智能、数字 媒体技术等.获省部级科技奖 2 项,出版 著作 3 部,发表学术论文 100 余篇. 李强,男,1987 年生,硕士研究生, 主要研究方向为网络智能. 刘洪涛,男,1974 年生,副教授,硕 士生导师,主要研究方向为社会计算、 群体智能和网络舆情,发表学术论文 10 余篇. ·550· 智 能 系 统 学 报 第 8 卷