智能系统：采用量子粒子群算法的潜器路径规划

第8卷第3期 智能系统学报 Vol.8 No.3 2013年6月 CAAI Transactions on Intelligent Systems Jun.2013 D0L:10.39696.issn.1673-4785.201206004 网络出版地址：http:/www.cnki..net/kcms/detail/23.1538.TP.20130515.0946.013.html 采用量子粒子群算法的潜器路径规划 邹梅魁，于飞，吕重阳，王兴彬 (哈尔滨工程大学理学院，黑龙江哈尔滨150001) 摘要：针对复杂海底环境中的潜器路径规划问题，提出了一种采用量子粒子群算法的潜器路径规划方法该方法首 先从海图中提取水深数据，基于自然邻点插值和随机中点位移插值得到密集规格水深数据.然后由此数据建立海底 三维模型，确定一个路径安全性检测方案及避碰原则，将海流大小方向对潜器航行的影响和路径点的转弯角度对航 行的影响转化为相应的路径长度.最后将总长度作为适应度函数，利用量子粒子群算法迭代来求取最优路径.仿真结 果得到了一条安全、简洁的路径，验证了该方法的有效性和可行性。 关键词：潜器：量子粒子群算法：海图：潜器导航；路径规划 中图分类号：TP242.6文献标志码：A文章编号：1673-4785(2013)03-0220-06 中文引用格式：邹梅魁，于飞，吕重阳，等.采用量子粒子群算法的潜器路径规划[J].智能系统学报，2013,8(3少220-225. 英文引用格式：ZOU Meikui,YU Fei,.LYU Chongyang,etal.Path planning for autonomous underwater vehicles by using QPSO [J].CAAI Transactions on Intelligent Systems,2013,8(3):220-225. Path planning for autonomous underwater vehicles by using QPSO ZOU Meikui,YU Fei,LYU Chongyang,WANG Xingbin (College of Science,Harbin Engineering University,Harbin 150001,China) Abstract:In efforts to address the submersible path planning problem in complex undersea environment,a path planning method for autonomous underwater vehicles was put forward,which is based on quantum-behaved particle swarm optimization (PSO).First,the bathymetric data was extracted from a nautical chart,and the intensive-spec- ification depth data was acquired by dealing with the natural neighbor interpolation and the random midpoint dis- placement interpolation.Next,we were able to establish the undersea 3D model and determine a path security tes- ting program,along with the principle to prevent collisions.The influence of the ocean current size,and direction on autonomous underwater vehicle navigation and the influence of the turning angle of the path points on navigation were transformed into corresponding path lengths.At last,the total length was used as the fitness function and the optimal path was obtained by iteration of quantum-behaved particle swarm optimization(QPSO).A safe and simple path was achieved as the result of the simulation,verifying effectiveness and feasibility of the method. Keywords:autonomous underwater vehicles;quantum-behaved particle swarm optimization;nautical chart;autono- mous underwater vehicle navigation;path planning 水下潜器路径规划是潜器智能化航行研究的一 量，这使得粒子进化方程形式变得更加简单，而且参 个重要课题.智能算法作为一种新型优化工具在该 数更少更容易控制，作为一种优化工具已在众多领 领域得到了广泛的应用).孙俊等受量子物理理论 域得到应用.本文利用量子粒子群算法对潜器路径 启发提出了量子粒子群算法[46]，该算法作为一种 进行寻优，首先基于海图水深数据建立海底模型，然 改进的粒子群算法具有更强的寻优能力和更快的收 后综合考虑影响航行的各个因素得到合适的适应度 敛速度.量子粒子群算法在进化过程中没有速度分 函数，并设计算法迭代步骤，最后进行仿真实验， 收稿日期：2012-06-05.网络出版日期：2013-05-15. 1基于海图数据建立海底模型 基金项目：国家自然科学基金资助项目(51179039)：高等学校博士学 科点专项科研基金资助项目(20102304110021). 为了更好地模拟真实海底环境，从电子海图中 通信作者：邹梅魁.E-mail:zoumeikui@126.com, 提取水深点数据，并对数据进行加工处理，最终依据

第 8 卷第 3 期 智 能 系 统 学 报 Vol.8 №.3 2013 年 6 月 CAAI Transactions on Intelligent Systems Jun. 2013 DOI:10.3969/j.issn.1673⁃4785.201206004 网络出版地址：http://www.cnki.net/kcms/detail/23.1538.TP.20130515.0946.013.html 采用量子粒子群算法的潜器路径规划 邹梅魁，于飞，吕重阳，王兴彬 （哈尔滨工程大学 理学院，黑龙江 哈尔滨 150001） 摘 要：针对复杂海底环境中的潜器路径规划问题，提出了一种采用量子粒子群算法的潜器路径规划方法.该方法首 先从海图中提取水深数据，基于自然邻点插值和随机中点位移插值得到密集规格水深数据.然后由此数据建立海底 三维模型，确定一个路径安全性检测方案及避碰原则，将海流大小方向对潜器航行的影响和路径点的转弯角度对航 行的影响转化为相应的路径长度.最后将总长度作为适应度函数，利用量子粒子群算法迭代来求取最优路径.仿真结 果得到了一条安全、简洁的路径，验证了该方法的有效性和可行性. 关键词：潜器；量子粒子群算法；海图；潜器导航；路径规划 中图分类号： TP242.6 文献标志码：A 文章编号：1673⁃4785(2013)03⁃0220⁃06 中文引用格式：邹梅魁，于飞，吕重阳，等.采用量子粒子群算法的潜器路径规划［J］.智能系统学报, 2013, 8(3): 220⁃225. 英文引用格式：ＺＯＵ Ｍｅｉｋｕｉ， ＹＵ Ｆｅｉ， ＬＹＵ Ｃｈｏｎｇｙａｎｇ， ｅｔ ａｌ． Ｐａｔｈ ｐｌａｎｎｉｎｇ ｆｏｒ ａｕｔｏｎｏｍｏｕｓ ｕｎｄｅｒｗａｔｅｒ ｖｅｈｉｃｌｅｓ ｂｙ ｕｓｉｎｇ ＱＰＳＯ ［Ｊ］． ＣＡＡＩ Ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ Ｉｎｔｅｌｌｉｇｅｎｔ Ｓｙｓｔｅｍｓ， ２０１３， ８（３）： ２２０⁃２２５． Ｐａｔｈ ｐｌａｎｎｉｎｇ ｆｏｒ ａｕｔｏｎｏｍｏｕｓ ｕｎｄｅｒｗａｔｅｒ ｖｅｈｉｃｌｅｓ ｂｙ ｕｓｉｎｇ ＱＰＳＯ ＺＯＵ Ｍｅｉｋｕｉ， ＹＵ Ｆｅｉ， ＬＹＵ Ｃｈｏｎｇｙａｎｇ， ＷＡＮＧ Ｘｉｎｇｂｉｎ （Ｃｏｌｌｅｇｅ ｏｆ Ｓｃｉｅｎｃｅ， Ｈａｒｂｉｎ Ｅｎｇｉｎｅｅｒｉｎｇ Ｕｎｉｖｅｒｓｉｔｙ， Ｈａｒｂｉｎ １５０００１， Ｃｈｉｎａ） Ａｂｓｔｒａｃｔ：Ｉｎ ｅｆｆｏｒｔｓ ｔｏ ａｄｄｒｅｓｓ ｔｈｅ ｓｕｂｍｅｒｓｉｂｌｅ ｐａｔｈ ｐｌａｎｎｉｎｇ ｐｒｏｂｌｅｍ ｉｎ ｃｏｍｐｌｅｘ ｕｎｄｅｒｓｅａ ｅｎｖｉｒｏｎｍｅｎｔ， ａ ｐａｔｈ ｐｌａｎｎｉｎｇ ｍｅｔｈｏｄ ｆｏｒ ａｕｔｏｎｏｍｏｕｓ ｕｎｄｅｒｗａｔｅｒ ｖｅｈｉｃｌｅｓ ｗａｓ ｐｕｔ ｆｏｒｗａｒｄ， ｗｈｉｃｈ ｉｓ ｂａｓｅｄ ｏｎ ｑｕａｎｔｕｍ⁃ｂｅｈａｖｅｄ ｐａｒｔｉｃｌｅ ｓｗａｒｍ ｏｐｔｉｍｉｚａｔｉｏｎ （ＰＳＯ）． Ｆｉｒｓｔ， ｔｈｅ ｂａｔｈｙｍｅｔｒｉｃ ｄａｔａ ｗａｓ ｅｘｔｒａｃｔｅｄ ｆｒｏｍ ａ ｎａｕｔｉｃａｌ ｃｈａｒｔ， ａｎｄ ｔｈｅ ｉｎｔｅｎｓｉｖｅ⁃ｓｐｅｃ⁃ ｉｆｉｃａｔｉｏｎ ｄｅｐｔｈ ｄａｔａ ｗａｓ ａｃｑｕｉｒｅｄ ｂｙ ｄｅａｌｉｎｇ ｗｉｔｈ ｔｈｅ ｎａｔｕｒａｌ ｎｅｉｇｈｂｏｒ ｉｎｔｅｒｐｏｌａｔｉｏｎ ａｎｄ ｔｈｅ ｒａｎｄｏｍ ｍｉｄｐｏｉｎｔ ｄｉｓ⁃ ｐｌａｃｅｍｅｎｔ ｉｎｔｅｒｐｏｌａｔｉｏｎ． Ｎｅｘｔ， ｗｅ ｗｅｒｅ ａｂｌｅ ｔｏ ｅｓｔａｂｌｉｓｈ ｔｈｅ ｕｎｄｅｒｓｅａ ３Ｄ ｍｏｄｅｌ ａｎｄ ｄｅｔｅｒｍｉｎｅ ａ ｐａｔｈ ｓｅｃｕｒｉｔｙ ｔｅｓ⁃ ｔｉｎｇ ｐｒｏｇｒａｍ， ａｌｏｎｇ ｗｉｔｈ ｔｈｅ ｐｒｉｎｃｉｐｌｅ ｔｏ ｐｒｅｖｅｎｔ ｃｏｌｌｉｓｉｏｎｓ． Ｔｈｅ ｉｎｆｌｕｅｎｃｅ ｏｆ ｔｈｅ ｏｃｅａｎ ｃｕｒｒｅｎｔ ｓｉｚｅ， ａｎｄ ｄｉｒｅｃｔｉｏｎ ｏｎ ａｕｔｏｎｏｍｏｕｓ ｕｎｄｅｒｗａｔｅｒ ｖｅｈｉｃｌｅ ｎａｖｉｇａｔｉｏｎ ａｎｄ ｔｈｅ ｉｎｆｌｕｅｎｃｅ ｏｆ ｔｈｅ ｔｕｒｎｉｎｇ ａｎｇｌｅ ｏｆ ｔｈｅ ｐａｔｈ ｐｏｉｎｔｓ ｏｎ ｎａｖｉｇａｔｉｏｎ ｗｅｒｅ ｔｒａｎｓｆｏｒｍｅｄ ｉｎｔｏ ｃｏｒｒｅｓｐｏｎｄｉｎｇ ｐａｔｈ ｌｅｎｇｔｈｓ． Ａｔ ｌａｓｔ， ｔｈｅ ｔｏｔａｌ ｌｅｎｇｔｈ ｗａｓ ｕｓｅｄ ａｓ ｔｈｅ ｆｉｔｎｅｓｓ ｆｕｎｃｔｉｏｎ ａｎｄ ｔｈｅ ｏｐｔｉｍａｌ ｐａｔｈ ｗａｓ ｏｂｔａｉｎｅｄ ｂｙ ｉｔｅｒａｔｉｏｎ ｏｆ ｑｕａｎｔｕｍ⁃ｂｅｈａｖｅｄ ｐａｒｔｉｃｌｅ ｓｗａｒｍ ｏｐｔｉｍｉｚａｔｉｏｎ （ＱＰＳＯ）． Ａ ｓａｆｅ ａｎｄ ｓｉｍｐｌｅ ｐａｔｈ ｗａｓ ａｃｈｉｅｖｅｄ ａｓ ｔｈｅ ｒｅｓｕｌｔ ｏｆ ｔｈｅ ｓｉｍｕｌａｔｉｏｎ， ｖｅｒｉｆｙｉｎｇ ｅｆｆｅｃｔｉｖｅｎｅｓｓ ａｎｄ ｆｅａｓｉｂｉｌｉｔｙ ｏｆ ｔｈｅ ｍｅｔｈｏｄ． Ｋｅｙｗｏｒｄｓ：ａｕｔｏｎｏｍｏｕｓ ｕｎｄｅｒｗａｔｅｒ ｖｅｈｉｃｌｅｓ； ｑｕａｎｔｕｍ⁃ｂｅｈａｖｅｄ ｐａｒｔｉｃｌｅ ｓｗａｒｍ ｏｐｔｉｍｉｚａｔｉｏｎ； ｎａｕｔｉｃａｌ ｃｈａｒｔ； ａｕｔｏｎｏ⁃ ｍｏｕｓ ｕｎｄｅｒｗａｔｅｒ ｖｅｈｉｃｌｅ ｎａｖｉｇａｔｉｏｎ； ｐａｔｈ ｐｌａｎｎｉｎｇ 收稿日期：２０１２⁃０６⁃０５． 网络出版日期：２０１３⁃０５⁃１５． 基金项目：国家自然科学基金资助项目（５１１７９０３９）；高等学校博士学 科点专项科研基金资助项目（２０１０２３０４１１００２１）． 通信作者：邹梅魁． Ｅ⁃ｍａｉｌ： ｚｏｕｍｅｉｋｕｉ＠ １２６．ｃｏｍ． 水下潜器路径规划是潜器智能化航行研究的一 个重要课题．智能算法作为一种新型优化工具在该 领域得到了广泛的应用［１⁃３］ ．孙俊等受量子物理理论 启发提出了量子粒子群算法［４⁃６］ ，该算法作为一种 改进的粒子群算法具有更强的寻优能力和更快的收 敛速度．量子粒子群算法在进化过程中没有速度分 量，这使得粒子进化方程形式变得更加简单，而且参 数更少更容易控制，作为一种优化工具已在众多领 域得到应用．本文利用量子粒子群算法对潜器路径 进行寻优，首先基于海图水深数据建立海底模型，然 后综合考虑影响航行的各个因素得到合适的适应度 函数，并设计算法迭代步骤，最后进行仿真实验． １ 基于海图数据建立海底模型 为了更好地模拟真实海底环境，从电子海图中 提取水深点数据，并对数据进行加工处理，最终依据

第3期 邹梅魁，等：采用量子粒子群算法的潜器路径规划 ·221· 海底标准网格点的水深数值建立海底三维模型 值，直到达到满意的数据点密度.利用MATLAB将 1.1水深数据的提取 得到的数据绘成海底三维地形图，如图1所示. 选取某海域电子海图作为研究对象，确定潜器 路径规划区域的经纬度范围，遍历与此区域有交集 -40 的所有海图的水深图层，读取并储存此区域内所有 -60 水深点的数据，由此得到潜器路径规划区域内各水 -80 深点的坐标及水深数值 -100 -120 由于从海图中得到的水深数据为无规律的离散 10080 数据点，为了便于计算和存储，需要对原始数据进行 60 40 20 20406080100 规格插值，利用文献[7-8]中介绍的基于自然邻点 y/km 0 x/水m Laplace插值方法，将得到的无规律离散数据点转化 图1海底三维模型 为等间距标准网格数据。 Fig.I Seabed of three-dimensional model 1.2对规格数据进行加密处理 2 模型处理 由于海图中的水深数据点比较稀疏，因而基于 自然邻点Laplace插值得到的标准网格数据点仍然 2.1海底模型处理 比较稀疏，不能满足精确导航的要求，故需要对1.1 为了方便模型的处理，在此模型中将潜器看作 中得到的数据进行加密处理，利用改进的随机中点 一个质点.但为了保证潜器安全航行，考虑到潜器的 位移法插值对数据点进行加密处理.由于文献 实际大小和模型水深数据的精度，对所有海底水深 [9]中介绍的菱形-方形细分法在进行插值时，只有 值进行减少10m处理，得到一个新的海底模型.这样 方形中心点插值考虑了四周点对它的影响，而对于 潜器可以贴着新的海底安全航行，即在规划中只要 边中心点插值只考虑其所在边的端点值对其的影 潜器路径点深度不大于该点新海底水深数据就视为 响，这使得处理后的数据只在单一方向（横向或纵 安全 向)上比较连续，而在另一方向上容易形成断层，具 2.2潜器航行过程中海流的影响 有一定局限性对标准网格数据进行加密处理时，基 潜器在航行过程中不可避免地受到海流的影 于文献[9]的算法进行了改进，对得到的规格数据 响，在航海上，一般将海流分成潮流、定海流、风生流 按如下步骤处理 等].由于定海流具有流向、流速固定性以及其他 1)将1.1节得到的规格网格数据记为水深数据 海流的不确定性，因此本文在进行静态路径规划时 集1，按式(1)计算所有规格数据网格中心点位置的 仅考虑定海流对潜器航行的影响. 水深数值，将得到的这些位置点数据加入到水深数 定海流对潜器航行的影响与其流速：及航行方 据集1中得到水深数据集2. 向与海流流向的夹角φ均有关.顺海流方向航行有 Hm=(H。+H。+H。+H)/4+Do:(1) 利于减少航行能量消耗，逆海流方向航行则需要更 式中：H。H。、H、H,为插值点周围4个点的水深值， 大的能耗，并且流向与航向所在直线夹角越大则产 D。为随机偏移量. 生的力矩越大，越不利于潜器控制.为了更好地在潜 2)水深数据集1中非边界边的中点均为水深 器路径规划中体现海流情况对路径规划的影响，根 数据集2中一个正方形的中心点，即此边的两端点 据海洋运载工具动力学规则波阻力分析，定义一个 与该点相邻的2个网格中心点构成正方形.此时该 简化的海流影响效益路径表示函数，将海流对潜器 类点也可以由式(1)计算得到其水深数据值 航行的影响转化为相应路径长度的增减.其函数表 3)对于边界上点，由于它仅有3个方向存在相 达式为 邻水深数值点，因而其只能看作为长方形一条边的 c:=a×v×l:×(bcos o-csin). (3) 中点，将计算公式改为式(2)进行计算. 式中：a表示海流-路径转化系数，b表示海流在潜 Hn=(H。+H。+H)/3+D。 (2) 器航行方向分量的影响系数，c表示海流在潜器航 通过改进，除边界上的点外其他所有的插值点 向垂直方向分量的影响系数.本文中参数a取0.15， 在进行插值时均考虑了4个方向数据点数值对其的 b取0.9，c取1.3. 影响，以及点在各个方向的连续性，使得地形曲面更 2.3潜器航行过程中角度限制及影响 加连续平滑. 考虑到潜器的灵活性，规划路径中路径点拐角 进行一轮这样的插值就能将原来的n×n数据 不能大于潜器允许的最大转弯角度山，设1，=(x: 加密为(2n-1)×(2n-1)数据.进行多轮这样的插 x-1yy-1,之-z-1)为第i路径的向量，若潜器允许

海底标准网格点的水深数值建立海底三维模型． １．１ 水深数据的提取 选取某海域电子海图作为研究对象，确定潜器 路径规划区域的经纬度范围，遍历与此区域有交集 的所有海图的水深图层，读取并储存此区域内所有 水深点的数据，由此得到潜器路径规划区域内各水 深点的坐标及水深数值． 由于从海图中得到的水深数据为无规律的离散 数据点，为了便于计算和存储，需要对原始数据进行 规格插值，利用文献［７⁃８］ 中介绍的基于自然邻点 Ｌａｐｌａｃｅ 插值方法，将得到的无规律离散数据点转化 为等间距标准网格数据． １．２ 对规格数据进行加密处理 由于海图中的水深数据点比较稀疏，因而基于 自然邻点 Ｌａｐｌａｃｅ 插值得到的标准网格数据点仍然 比较稀疏，不能满足精确导航的要求，故需要对 １．１ 中得到的数据进行加密处理，利用改进的随机中点 位移法插值［９］ 对数据点进行加密处理． 由于文献 ［９］中介绍的菱形－方形细分法在进行插值时，只有 方形中心点插值考虑了四周点对它的影响，而对于 边中心点插值只考虑其所在边的端点值对其的影 响，这使得处理后的数据只在单一方向（横向或纵 向）上比较连续，而在另一方向上容易形成断层，具 有一定局限性．对标准网格数据进行加密处理时，基 于文献［９］的算法进行了改进，对得到的规格数据 按如下步骤处理． １）将 １．１ 节得到的规格网格数据记为水深数据 集 １，按式（１）计算所有规格数据网格中心点位置的 水深数值，将得到的这些位置点数据加入到水深数 据集 １ 中得到水深数据集 ２． Ｈｍ ＝ （Ｈａ ＋ Ｈｂ ＋ Ｈｃ ＋ Ｈｄ ） ／ ４ ＋ Ｄ０ ． （１） 式中：Ｈａ 、Ｈｂ、Ｈｃ、Ｈｄ 为插值点周围 ４ 个点的水深值， Ｄｏ 为随机偏移量． ２）水深数据集 １ 中非边界边的中点均为水深 数据集 ２ 中一个正方形的中心点，即此边的两端点 与该点相邻的 ２ 个网格中心点构成正方形．此时该 类点也可以由式（１）计算得到其水深数据值． ３）对于边界上点，由于它仅有 ３ 个方向存在相 邻水深数值点，因而其只能看作为长方形一条边的 中点，将计算公式改为式（２）进行计算． Ｈｍ ＝ （Ｈａ ＋ Ｈｂ ＋ Ｈｃ） ／ ３ ＋ Ｄ ∗ ０ ． （２） 通过改进，除边界上的点外其他所有的插值点 在进行插值时均考虑了 ４ 个方向数据点数值对其的 影响，以及点在各个方向的连续性，使得地形曲面更 加连续平滑． 进行一轮这样的插值就能将原来的 ｎ×ｎ 数据 加密为（２ｎ－ １） ×（２ｎ － １） 数据．进行多轮这样的插 值，直到达到满意的数据点密度．利用 ＭＡＴＬＡＢ 将 得到的数据绘成海底三维地形图，如图 １ 所示． 图 １ 海底三维模型 Ｆｉｇ．１ Ｓｅａｂｅｄ ｏｆ ｔｈｒｅｅ⁃ｄｉｍｅｎｓｉｏｎａｌ ｍｏｄｅｌ ２ 模型处理 ２．１ 海底模型处理 为了方便模型的处理，在此模型中将潜器看作 一个质点．但为了保证潜器安全航行，考虑到潜器的 实际大小和模型水深数据的精度，对所有海底水深 值进行减少１０ ｍ处理，得到一个新的海底模型．这样 潜器可以贴着新的海底安全航行，即在规划中只要 潜器路径点深度不大于该点新海底水深数据就视为 安全． ２．２ 潜器航行过程中海流的影响 潜器在航行过程中不可避免地受到海流的影 响，在航海上，一般将海流分成潮流、定海流、风生流 等［１０］ ．由于定海流具有流向、流速固定性以及其他 海流的不确定性，因此本文在进行静态路径规划时 仅考虑定海流对潜器航行的影响． 定海流对潜器航行的影响与其流速 ｖ 及航行方 向与海流流向的夹角 φ 均有关．顺海流方向航行有 利于减少航行能量消耗，逆海流方向航行则需要更 大的能耗，并且流向与航向所在直线夹角越大则产 生的力矩越大，越不利于潜器控制．为了更好地在潜 器路径规划中体现海流情况对路径规划的影响，根 据海洋运载工具动力学规则波阻力分析，定义一个 简化的海流影响效益路径表示函数，将海流对潜器 航行的影响转化为相应路径长度的增减．其函数表 达式为 ｃｉ ＝ ａ × ｖ × ｌ ｉ × （ｂｃｏｓ φ － ｃｓｉｎ φ）． （３） 式中：ａ 表示海流－路径转化系数，ｂ 表示海流在潜 器航行方向分量的影响系数，ｃ 表示海流在潜器航 向垂直方向分量的影响系数．本文中参数 ａ 取 ０．１５， ｂ 取 ０．９，ｃ 取 １．３． ２．３ 潜器航行过程中角度限制及影响 考虑到潜器的灵活性，规划路径中路径点拐角 不能大于潜器允许的最大转弯角度［１］ ，设 ｌ ｉ ＝ （ ｘｉ － ｘｉ－１ ，ｙｉ －ｙｉ－１ ，ｚｉ －ｚｉ－１ ）为第 ｉ 路径的向量，若潜器允许 第 ３ 期 邹梅魁，等：采用量子粒子群算法的潜器路径规划 ·２２１·

·222· 智能系统学报 第8卷 的最大转弯角为0，则路径点拐角应满足式(4)： 同时粒子的速度受到一定的限制，使得粒子的搜索 L 空间是一个有限的并逐渐减小的区域，不能覆盖整 111l11 ≤c0s0nmx,i=1,2,…,n. (4) 个可行解空间，从而PS0算法不能保证全局收 此外考虑到潜器在转弯过程中，需要提供额外 敛[5，山.针对PS0算法的这个缺点，孙俊等受量子物 的动力且水平方向与竖直方向的转弯动力不一样， 理理论启发提出了一种改进的粒子群优化算法一 角度越大所耗能量越大.为了评价航行轨迹曲度对 量子粒子群算法(quantum-behaved particle swarm 优化路径的影响，根据潜器动力学分析，定义一个路 optimization,QPS0).其粒子进化方程为： 径曲度惩罚函数，将每次转弯能耗转化为相应的路 X,(t+1)=P±aC(t)-X,(t)·ln[l/u,(t)], 径长度，曲度惩罚路径表示函数为 (7) 0:=A×l:×(atan8:+Btan8:). (5) p=中(t)·P(t)+[1-中(t)]·G(t),(8) 式中：A为角度-路径转换系数，α为水平方向转弯 c40=方2P,o0 (9) 成本系数，日为水平转弯角，B为竖直方向转弯成本 系数，9为竖直转弯角.本文中参数A取0.2，α取 式中：X(t)(i=1,2,…,N,j=1,2,…,M)为第i个 0.2,B取2. 粒子t时刻在第j维搜索空间的位置，N为搜索空间 2.4规划路径安全性要求 维数，M为粒子群体个数；中(t)~U(0,1),4(t)~ 为了保证潜器安全航行，潜器路径规划中每一 U(0,1),C(t)为粒子的平均最好位置，P(t)为粒 段路径线段必须避免与海底面相碰撞.设1=(x, 子i的个体最优解P(t)的第j维空间分量，G,(t)为 x-1,y:y-1,--1)为第i段路径线段S={s∈Z1s∈ 群体最优解G(t)的第j维空间分量：α为收缩-扩 [x-1,x:]},当x取值x,∈S时，由直线上点的坐标 张系数(CE coefficient),它是算法除群体规模和迭 公式计算可得路径中对应点的坐标(x,y,,).若路 代次数以外的惟一控制参数，对参数α控制可以采 径线段不与海底曲面相交，必须使路径中每一点的 用固定取值和线性减少的方式[)，在此本文参照文 位置深度小于该点的海底水深由于在海底模型中 献[l2]中方法，取a线性递减为a=amin+(mx- 仅知道标准网格上点的水深，因而只能将路径线段 amn）×(Tx-t)/Tmx·其中取&in=0.5,&mx=1,Tmn 上点的坐标与相邻的标准网格点水深作比较.设 为最大迭代次数，t为当前迭代次数， y=f(y,),y2=f(y:)+1,其中f(y,)为y.的整数部 3.2导航算法步骤 分.若对任意s∈S均满足a,<h(x=xy=y1),且之，<h 1)确定路径起点P。(x,yo,0)和目标点 (x=x,y=y2),则该路径线段与海底无交点 P(x,yn,2n).对海底模型环境进行分割处理，连接 2.5适应度函数 线段P。P.并对其进行n等分，并在每个等分点处作 根据上述分析，由于要综合考虑路径长度、海流 垂直x轴的平面并记为Ⅱ(P=1,2,…,n-1).共选 效益、路径点曲度三者来规划一条最优路径.因此定 取N个粒子进行T次迭代计算来求取最优路径.对 义一个综合路径长度∫，其值为粒子的总路径长度、 任意粒子i而言，其位置为在各平面上均取一点所 总曲度惩罚路径表示函数值及总海流效益路径表示 组成的点集{(x1y1,1),（x2,y2,2),…,（x-1y-1 函数值三者之和.由于在式(3)和式(5)中，海流影 -1){.粒子i的初始位置定义为在任意平面P上随 响效益和路径点曲度惩罚已转化为相应的路径长度 机选取一个初始位置点X(0),设为(x,y,z).由于 值，因而总路径长度为 该平面上所有点的x值相同，则相当于随机定义一 f2++ 个二元数(y,z).对该位置点的高度值z进行检验， 6) 判断z值是否大于(x,y)点处的水深值，若不满足则 式中：山，为第i段路径长度， 舍去，并对该点位置继续进行随机选择，直到所有粒 4=√(x:-x-1)2+(y:--1)2+(2--1)2; 子在每个平面上的初始位置都大于所在点的水深 c:为第i段路径海流效益路径转换值；心，为路径点 此时粒子迭代次数为t=1. i的转弯成本路径转换值， 2)对任意粒子，连接该粒子在相邻平面上的位 置点即构成了该粒子搜索的路径线段，检查此路径 3导航算法及步骤 线段是否满足2.4节中的路径安全性要求，若不满 3.1量子粒子群算法 足安全条件则将路径中与海底相交部分的线段端点 在PS0算法中，粒子的运动状态由位置和速度 进行变异处理，将线段端点坐标中z值各增加一个 描述，随着时间的演化，粒子的运动轨迹是既定的： 单位长度.再次对其进行安全性判断，若仍不满足安

的最大转弯角为 θｍａｘ，则路径点拐角应满足式（４）： ｌ ｉ ｌ Ｔ ｉ＋１ ｜ ｌ ｉ ｜·｜ ｌ ｉ＋１ ｜ ≤ ｃｏｓ θｍａｘ，ｉ ＝ １，２，…，ｎ． （４） 此外考虑到潜器在转弯过程中，需要提供额外 的动力且水平方向与竖直方向的转弯动力不一样， 角度越大所耗能量越大．为了评价航行轨迹曲度对 优化路径的影响，根据潜器动力学分析，定义一个路 径曲度惩罚函数，将每次转弯能耗转化为相应的路 径长度，曲度惩罚路径表示函数为 ｗｉ ＝ Ａ × ｌ ｉ × （αｔａｎ θｉ ＋ βｔａｎ ϑｉ）． （５） 式中：Ａ 为角度－路径转换系数，α 为水平方向转弯 成本系数，θｉ 为水平转弯角，β 为竖直方向转弯成本 系数，ϑｉ 为竖直转弯角．本文中参数 Ａ 取 ０．２，α 取 ０．２，β 取 ２． ２．４ 规划路径安全性要求 为了保证潜器安全航行，潜器路径规划中每一 段路径线段必须避免与海底面相碰撞．设 ｌ ｉ ＝ （ ｘｉ － ｘｉ－１ ，ｙｉ －ｙｉ－１ ，ｚｉ －ｚｉ－１ ）为第 ｉ 段路径线段．Ｓ ＝ ｛ｓ∈Ｚ ｜ｓ∈ ［ｘｉ－１ ，ｘｉ］｝，当 ｘ 取值 ｘｓ∈Ｓ 时，由直线上点的坐标 公式计算可得路径中对应点的坐标（ ｘｓ，ｙｓ，ｚｓ）．若路 径线段不与海底曲面相交，必须使路径中每一点的 位置深度小于该点的海底水深．由于在海底模型中 仅知道标准网格上点的水深，因而只能将路径线段 上点的坐标与相邻的标准网格点水深作比较． 设 ｙｓ１ ＝ ｆ（ｙｓ），ｙｓ２ ＝ ｆ（ ｙｓ） ＋１，其中 ｆ（ ｙｓ ） 为 ｙｓ 的整数部 分．若对任意 ｓ∈Ｓ 均满足 ｚｓ＜ｈ（ｘ ＝ ｘｓ，ｙ ＝ ｙｓ１ ），且ｚｓ＜ｈ （ｘ ＝ ｘｓ，ｙ ＝ ｙｓ２ ），则该路径线段与海底无交点． ２．５ 适应度函数 根据上述分析，由于要综合考虑路径长度、海流 效益、路径点曲度三者来规划一条最优路径．因此定 义一个综合路径长度 ｆ，其值为粒子的总路径长度、 总曲度惩罚路径表示函数值及总海流效益路径表示 函数值三者之和．由于在式（３）和式（５）中，海流影 响效益和路径点曲度惩罚已转化为相应的路径长度 值，因而总路径长度为 ｆ ＝ ∑ ｎ ｉ ＝ １ ｌ ｉ ＋ ∑ ｎ ｉ ＝ １ ｃｉ ＋ ∑ ｎ－１ ｉ ＝ ０ ｗｉ ． （６） 式中：ｌ ｉ 为第 ｉ 段路径长度， ｌ ｉ ＝ （ｘｉ － ｘｉ－１） ２ ＋ （ｙｉ － ｙｉ－１） ２ ＋ （ｚｉ － ｚｉ－１） ２ ； ｃｉ 为第 ｉ 段路径海流效益路径转换值； ｗｉ 为路径点 ｉ 的转弯成本路径转换值． ３ 导航算法及步骤 ３．１ 量子粒子群算法 在 ＰＳＯ 算法中，粒子的运动状态由位置和速度 描述，随着时间的演化，粒子的运动轨迹是既定的； 同时粒子的速度受到一定的限制，使得粒子的搜索 空间是一个有限的并逐渐减小的区域，不能覆盖整 个可行解空间， 从而 ＰＳＯ 算法不能保证全局收 敛［５，１１］ ．针对 ＰＳＯ 算法的这个缺点，孙俊等受量子物 理理论启发提出了一种改进的粒子群优化算法——— 量子粒子群算法 （ ｑｕａｎｔｕｍ⁃ｂｅｈａｖｅｄ ｐａｒｔｉｃｌｅ ｓｗａｒｍ ｏｐｔｉｍｉｚａｔｉｏｎ， ＱＰＳＯ）．其粒子进化方程为： Ｘｉｊ（ｔ ＋ １） ＝ ｐｉｊ ± α Ｃｊ（ｔ） － Ｘｉｊ（ｔ） ·ｌｎ［１ ／ ｕｉｊ（ｔ）］， （７） ｐｉｊ ＝ ϕｊ（ｔ）·Ｐｉｊ（ｔ） ＋ ［１ － ϕｊ（ｔ）］·Ｇｊ（ｔ）， （８） Ｃｊ（ｔ） ＝ １ Ｎ∑ Ｎ ｉ ＝ １ Ｐｉｊ（ｔ）． （９） 式中：Ｘｉｊ（ ｔ） （ ｉ ＝ １，２，…，Ｎ，ｊ ＝ １，２，…，Ｍ）为第 ｉ 个 粒子 ｔ 时刻在第 ｊ 维搜索空间的位置，Ｎ 为搜索空间 维数，Ｍ 为粒子群体个数；ϕｊ（ｔ） ～ Ｕ（０，１），ｕｉｊ（ ｔ） ～ Ｕ（０，１），Ｃｊ（ｔ）为粒子的平均最好位置，Ｐｉｊ（ ｔ） 为粒 子 ｉ 的个体最优解 Ｐｉ（ｔ）的第 ｊ 维空间分量，Ｇｊ（ｔ）为 群体最优解 Ｇ（ ｔ）的第 ｊ 维空间分量；α 为收缩－扩 张系数（ＣＥ ｃｏｅｆｆｉｃｉｅｎｔ），它是算法除群体规模和迭 代次数以外的惟一控制参数，对参数 α 控制可以采 用固定取值和线性减少的方式［１２］ ，在此本文参照文 献［１２］ 中方法，取 α 线性递减为 α ＝ αｍｉｎ ＋（ αｍａｘ － αｍｉｎ ）×（Ｔｍａｘ －ｔ） ／ Ｔｍａｘ ．其中取 αｍｉｎ ＝ ０．５，αｍａｘ ＝ １，Ｔｍａｘ 为最大迭代次数，ｔ 为当前迭代次数． ３．２ 导航算法步骤 １） 确 定 路 径 起 点 Ｐ０ （ ｘ０ ， ｙ０ ， ｚ０ ） 和 目 标 点 Ｐｎ（ｘｎ ，ｙｎ ，ｚｎ ）．对海底模型环境进行分割处理，连接 线段 Ｐ０Ｐｎ 并对其进行 ｎ 等分，并在每个等分点处作 垂直 ｘ 轴的平面并记为 ΠＰ（Ｐ ＝ １，２，…，ｎ－１）．共选 取 Ｎ 个粒子进行 Ｔ 次迭代计算来求取最优路径．对 任意粒子 ｉ 而言，其位置为在各平面上均取一点所 组成的点集｛（ｘ１ ，ｙ１ ，ｚ１ ），（ｘ２ ，ｙ２ ，ｚ２ ），…，（ｘｎ－１ ，ｙｎ－１ ， ｚｎ－１ ）｝．粒子 ｉ 的初始位置定义为在任意平面 Ｐ 上随 机选取一个初始位置点 ＸｉＰ（０），设为（ｘ，ｙ，ｚ）．由于 该平面上所有点的 ｘ 值相同，则相当于随机定义一 个二元数（ｙ，ｚ）．对该位置点的高度值 ｚ 进行检验， 判断 ｚ 值是否大于（ｘ，ｙ）点处的水深值，若不满足则 舍去，并对该点位置继续进行随机选择，直到所有粒 子在每个平面上的初始位置都大于所在点的水深． 此时粒子迭代次数为 ｔ ＝ １． ２）对任意粒子，连接该粒子在相邻平面上的位 置点即构成了该粒子搜索的路径线段，检查此路径 线段是否满足 ２．４ 节中的路径安全性要求，若不满 足安全条件则将路径中与海底相交部分的线段端点 进行变异处理，将线段端点坐标中 ｚ 值各增加一个 单位长度．再次对其进行安全性判断，若仍不满足安 ·２２２· 智 能 系 统 学 报 第 ８ 卷

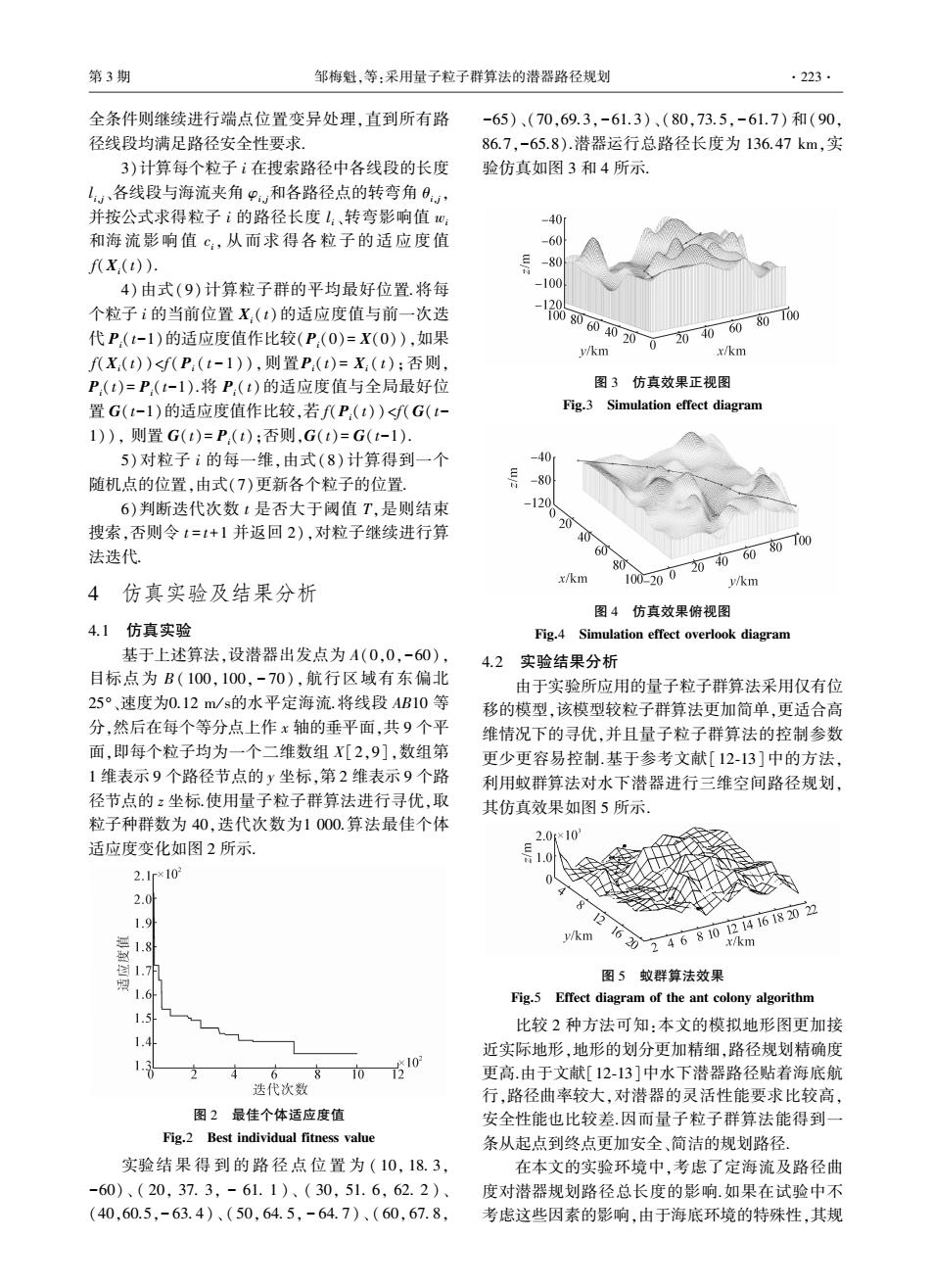
第3期 邹梅魁，等：采用量子粒子群算法的潜器路径规划 ·223· 全条件则继续进行端点位置变异处理，直到所有路 -65)、(70,69.3,-61.3)、(80,73.5,-61.7)和(90 径线段均满足路径安全性要求」 86.7,-65.8).潜器运行总路径长度为136.47km,实 3)计算每个粒子i在搜索路径中各线段的长度 验仿真如图3和4所示. ,、各线段与海流夹角9和各路径点的转弯角0， 并按公式求得粒子i的路径长度l:、转弯影响值心： -40 和海流影响值℃：，从而求得各粒子的适应度值 -60 f(x(t)). -80 4)由式(9)计算粒子群的平均最好位置.将每 -100 个粒子i的当前位置X,(t)的适应度值与前一次选 代P,(t-1)的适应度值作比较(P,(0)=X(0)),如果 604020020406080100 y/km x/km f(X(t))<f(P:(t-1)),则置P(t)=X(t):否则， P(t)=P(t-1).将P(t)的适应度值与全局最好位 图3仿真效果正视图 置G(t-1)的适应度值作比较，若f八P,(t))<f(G(t- Fig.3 Simulation effect diagram 1)),则置G(t)=P(t);否则，G(t)=G(t-1): 5)对粒子i的每一维，由式(8)计算得到一个 -40 随机点的位置，由式(7)更新各个粒子的位置 -80 6)判断迭代次数t是否大于阈值T,是则结束 12 搜索，否则令t=t+1并返回2)，对粒子继续进行算 20 40心 法迭代 60 10d2002006080700 x/km y/km 4仿真实验及结果分析 图4仿真效果俯视图 4.1仿真实验 Fig.4 Simulation effect overlook diagram 基于上述算法，设潜器出发点为A(0,0,-60), 4.2实验结果分析 目标点为B(100,100,-70),航行区域有东偏北 由于实验所应用的量子粒子群算法采用仅有位 25°、速度为0.12m/s的水平定海流.将线段AB10等 移的模型，该模型较粒子群算法更加简单，更适合高 分，然后在每个等分点上作x轴的垂平面，共9个平 维情况下的寻优，并且量子粒子群算法的控制参数 面，即每个粒子均为一个二维数组X[2,9],数组第 更少更容易控制.基于参考文献[12-13]中的方法， 1维表示9个路径节点的y坐标，第2维表示9个路 利用蚁群算法对水下潜器进行三维空间路径规划， 径节点的z坐标使用量子粒子群算法进行寻优，取 其仿真效果如图5所示. 粒子种群数为40，迭代次数为1000.算法最佳个体 2.0×10 适应度变化如图2所示 1.0 2.1rx10 2.0 1.9 y/km 824681021416182022 6 x/km 1.7 图5蚁群算法效果 1.6 Fig.5 Effect diagram of the ant colony algorithm 1.5 比较2种方法可知：本文的模拟地形图更加接 1.4 近实际地形，地形的划分更加精细，路径规划精确度 68 0 更高.由于文献[12-13]中水下潜器路径贴着海底航 迭代次数 行，路径曲率较大，对潜器的灵活性能要求比较高， 图2最佳个体适应度值 安全性能也比较差.因而量子粒子群算法能得到一 Fig.2 Best individual fitness value 条从起点到终点更加安全、简洁的规划路径 实验结果得到的路径点位置为(10,18.3， 在本文的实验环境中，考虑了定海流及路径曲 -60)、(20,37.3,-61.1)、(30,51.6,62.2)、 度对潜器规划路径总长度的影响.如果在试验中不 (40,60.5.-63.4)、(50.64.5,-64.7)、(60,67.8, 考虑这些因素的影响，由于海底环境的特殊性，其规

全条件则继续进行端点位置变异处理，直到所有路 径线段均满足路径安全性要求． ３）计算每个粒子 ｉ 在搜索路径中各线段的长度 ｌ ｉ，ｊ、各线段与海流夹角 φｉ，ｊ和各路径点的转弯角 θｉ，ｊ， 并按公式求得粒子 ｉ 的路径长度 ｌ ｉ、转弯影响值 ｗｉ 和海流影响值 ｃｉ， 从而求得 各 粒 子 的 适 应 度 值 ｆ（Ｘｉ（ｔ））． ４） 由式（９） 计算粒子群的平均最好位置．将每 个粒子 ｉ 的当前位置 Ｘｉ（ ｔ）的适应度值与前一次迭 代 Ｐｉ（ｔ－１）的适应度值作比较（Ｐｉ（０）＝ Ｘ（０）），如果 ｆ（Ｘｉ（ｔ））＜ｆ（ Ｐｉ （ ｔ － １）），则置Ｐｉ（ｔ）＝ Ｘｉ （ ｔ）；否则， Ｐｉ（ｔ）＝ Ｐｉ（ｔ－１）．将 Ｐｉ（ ｔ）的适应度值与全局最好位 置 Ｇ（ｔ－１）的适应度值作比较，若 ｆ（Ｐｉ（ｔ）） ＜ｆ（Ｇ（ｔ－ １））， 则置 Ｇ（ｔ）＝ Ｐｉ（ｔ）；否则，Ｇ（ｔ）＝ Ｇ（ｔ－１）． ５）对粒子 ｉ 的每一维，由式（８） 计算得到一个 随机点的位置，由式（７）更新各个粒子的位置． ６）判断迭代次数 ｔ 是否大于阈值 Ｔ，是则结束 搜索，否则令 ｔ ＝ ｔ＋１ 并返回 ２），对粒子继续进行算 法迭代． ４ 仿真实验及结果分析 ４．１ 仿真实验 基于上述算法，设潜器出发点为 Ａ（０，０，－６０）， 目标点为 Ｂ （ １００，１００， － ７０），航行区域有东偏北 ２５°、速度为０．１２ ｍ ／ ｓ的水平定海流．将线段 ＡＢ１０ 等 分，然后在每个等分点上作 ｘ 轴的垂平面，共 ９ 个平 面，即每个粒子均为一个二维数组 Ｘ［２，９］，数组第 １ 维表示 ９ 个路径节点的 ｙ 坐标，第 ２ 维表示 ９ 个路 径节点的 ｚ 坐标．使用量子粒子群算法进行寻优，取 粒子种群数为 ４０，迭代次数为１ ０００．算法最佳个体 适应度变化如图 ２ 所示． 图 ２ 最佳个体适应度值 Ｆｉｇ．２ Ｂｅｓｔ ｉｎｄｉｖｉｄｕａｌ ｆｉｔｎｅｓｓ ｖａｌｕｅ 实验结 果 得 到 的 路 径 点 位 置 为 （ １０， １８． ３， －６０）、 （ ２０， ３７． ３， － ６１． １ ）、 （ ３０， ５１． ６， ６２． ２ ）、 （４０，６０．５，－ ６３． ４）、 （ ５０， ６４． ５， － ６４． ７）、 （ ６０， ６７． ８， －６５）、（７０，６９．３，－６１．３）、（８０，７３．５，－６１．７） 和（９０， ８６．７，－６５．８）．潜器运行总路径长度为 １３６．４７ ｋｍ，实 验仿真如图 ３ 和 ４ 所示． 图 ３ 仿真效果正视图 Ｆｉｇ．３ Ｓｉｍｕｌａｔｉｏｎ ｅｆｆｅｃｔ ｄｉａｇｒａｍ 图 ４ 仿真效果俯视图 Ｆｉｇ．４ Ｓｉｍｕｌａｔｉｏｎ ｅｆｆｅｃｔ ｏｖｅｒｌｏｏｋ ｄｉａｇｒａｍ ４．２ 实验结果分析 由于实验所应用的量子粒子群算法采用仅有位 移的模型，该模型较粒子群算法更加简单，更适合高 维情况下的寻优，并且量子粒子群算法的控制参数 更少更容易控制．基于参考文献［１２⁃１３］中的方法， 利用蚁群算法对水下潜器进行三维空间路径规划， 其仿真效果如图 ５ 所示． 图 ５ 蚁群算法效果 Ｆｉｇ．５ Ｅｆｆｅｃｔ ｄｉａｇｒａｍ ｏｆ ｔｈｅ ａｎｔ ｃｏｌｏｎｙ ａｌｇｏｒｉｔｈｍ 比较 ２ 种方法可知：本文的模拟地形图更加接 近实际地形，地形的划分更加精细，路径规划精确度 更高．由于文献［１２⁃１３］中水下潜器路径贴着海底航 行，路径曲率较大，对潜器的灵活性能要求比较高， 安全性能也比较差．因而量子粒子群算法能得到一 条从起点到终点更加安全、简洁的规划路径． 在本文的实验环境中，考虑了定海流及路径曲 度对潜器规划路径总长度的影响．如果在试验中不 考虑这些因素的影响，由于海底环境的特殊性，其规 第 ３ 期 邹梅魁，等：采用量子粒子群算法的潜器路径规划 ·２２３·

·224· 智能系统学报 第8卷 划范围可看成一个长方体空间，该空间的长宽为千 haved particle swarm optimization:analysis of the individual 米级，而高度为米级若只考虑单纯总路径长度，其 particle's behavior and parameter selection[].Evolutionary 结果将是沿着起点与终点的连线，向上避开海底障 Computation,2012,20(3):349-393. 碍而得到的一条最短路径，其仿真结果如图6所示 [6]CHAI Zhilei,SUN Jun,CAI Rui,et al.Implementing quantum-behaved particle swarm optimization algorithm in -40 FPGA for embedded real-time applications[C]//Proceed- -60 ings of the 2009 Fourth International Computer Sciences -80 -100 and Convergence Information Technology.Washington, DC.USA:IEEE Computer Society,2009:886-890. -120 10080604020.20406080700 [7]申浩，田峰敏，赵玉新.基于VoronoiCells插值的三维海底 地形图生成方法[J].系统仿真学报，2006,18(2)：444- y/km x/km 446. 图6仿真效果 SHEN Hao,TIAN Fengmin,ZHAO Yuxin.Method for gen- Fig.6 Simulation effect diagram erating 3D digital map based upon VoronoiCells[J].Journal of System Simulation,2006,18(2):444-446. 5结束语 [8]姜辉.水下潜器路径规划仿真平台的设计与实现[D].哈 本文对从海图中提取的水深数据进行处理建立 尔滨：哈尔滨工程大学，2009 更加真实的海底三维模型，利用量子粒子群算法进 JIANG Hui.Design and implementation of the simulation 行水下潜器在海底三维模型中的路径寻优，仿真结 platform for underwater vehicle path planning[D].Harbin: 果表明了量子粒子群算法能较好地实现水下潜器全 Harbin Engineering University,2009. 局路径规划本文仅就已知海底环境进行全局路径 [9]梁俊，王琦，刘坤良，等基于随机中点位移法的三维地形 模拟[J].计算机仿真，2005,22(1)：213-215 规划，对于复杂的充满动态障碍物的海洋环境下实 LIANG Jun,WANG Qi,LIU Kunliang,et al.3D terrain 时的潜器导航还有待进一步研究. simulation based on the method of random mid-point dis- 参考文献： placement[J].Computer Simulation,2005,22(1):213- 215. [1]于飞，唐小勇，潘洪悦改进粒子群算法在三维水下导航 [10]毛宇峰，庞永杰.改进粒子群算法在水下机器人路径规 规划中的应用[J].北京理工大学学报，2010,30(9)： 划中的应用J].计算机应用，2010,30(3)：789-792. 1059-1063 MAO Yufeng,PANG Yongjie.Application of improved YU Fei,TANG Xiaoyong,PAN Hongyue.The application particle swam optimization in path planning of underwater of an improved PSO to the submersible path-planning[J]. vehicles[J].Joural of Computer Applications,2010,30 Transactions of Beijing Institute of Technology,2010,30 (3):789-792 (9):1059-1063. [11]VAN DEN BERGH F,ENGELBRECHT A P.A new local- [2]唐小勇，于飞，潘洪悦改进粒子群算法的潜器导航规划 ly convergent particle swarm optimizer[C]//IEEE Interna- [J].智能系统学报，2010,5(5)：443447. tional Conference on Systems,Man and Cybernetics.Ham- TANG Xiaoyong,YU Fei,PAN Hongyue.Submersible mamet,Tunisia,2002,3:94-99. path-planning based on an improved PSO[J].CAAI Trans- [12]WARREN C W.A technique for autonomous underwater actions on Intelligent Systems,2010,5(5):443-447. vehicle route planning[J].IEEE Journal of Oceanic Engi- [3]赵百轶，张利军，贾鹤鸣.基于四叉树和改进蚊群算法的 neering,1990,15(3):199-204. 全局路径规划[J].应用科技，2011,38(10)：23-28. [13]VASUDEVAN C.GANESAN L.Case-based path planning ZHAO Baiyi,ZHANG Lijun,JIA Heming.Global path for autonomous underwater vehicles[J].Autonomous Ro- planning based on quadtree and improved ant colony optimi- bots,1996.3(2):79-89. zation algorithm [J].Applied Science and Technology, 作者简介： 2011,38(10):23-28 邹梅魁，男，1988年生，硕士研究 [4]SUN Jun,XU Wenbo,FENG Bin.A global search strategy 生，主要研究方向为水下潜器三维路径 of quantum-behaved particle swarm optimization[C//Pro- 规划. ceedings of the IEEE Conference on Cybernetics and Intelli- gent Systems.Singapore,2004:111-116. [5]SUN Jun,FANG Wei,WU Xiaojun,et al.Quantum-be-

划范围可看成一个长方体空间，该空间的长宽为千 米级，而高度为米级．若只考虑单纯总路径长度，其 结果将是沿着起点与终点的连线，向上避开海底障 碍而得到的一条最短路径，其仿真结果如图 ６ 所示． 图 ６ 仿真效果 Ｆｉｇ．６ Ｓｉｍｕｌａｔｉｏｎ ｅｆｆｅｃｔ ｄｉａｇｒａｍ ５ 结束语 本文对从海图中提取的水深数据进行处理建立 更加真实的海底三维模型，利用量子粒子群算法进 行水下潜器在海底三维模型中的路径寻优，仿真结 果表明了量子粒子群算法能较好地实现水下潜器全 局路径规划．本文仅就已知海底环境进行全局路径 规划，对于复杂的充满动态障碍物的海洋环境下实 时的潜器导航还有待进一步研究． 参考文献： ［１］于飞，唐小勇，潘洪悦．改进粒子群算法在三维水下导航 规划中的应用［ Ｊ］．北京理工大学学报， ２０１０， ３０（ ９）： １０５９⁃１０６３． ＹＵ Ｆｅｉ， ＴＡＮＧ Ｘｉａｏｙｏｎｇ， ＰＡＮ Ｈｏｎｇｙｕｅ． Ｔｈｅ ａｐｐｌｉｃａｔｉｏｎ ｏｆ ａｎ ｉｍｐｒｏｖｅｄ ＰＳＯ ｔｏ ｔｈｅ ｓｕｂｍｅｒｓｉｂｌｅ ｐａｔｈ⁃ｐｌａｎｎｉｎｇ［ Ｊ］． Ｔｒａｎｓａｃｔｉｏｎｓ ｏｆ Ｂｅｉｊｉｎｇ Ｉｎｓｔｉｔｕｔｅ ｏｆ Ｔｅｃｈｎｏｌｏｇｙ， ２０１０， ３０ （９）： １０５９⁃１０６３． ［２］唐小勇，于飞，潘洪悦．改进粒子群算法的潜器导航规划 ［Ｊ］．智能系统学报， ２０１０， ５（５）： ４４３⁃４４７． ＴＡＮＧ Ｘｉａｏｙｏｎｇ， ＹＵ Ｆｅｉ， ＰＡＮ Ｈｏｎｇｙｕｅ． Ｓｕｂｍｅｒｓｉｂｌｅ ｐａｔｈ⁃ｐｌａｎｎｉｎｇ ｂａｓｅｄ ｏｎ ａｎ ｉｍｐｒｏｖｅｄ ＰＳＯ［Ｊ］． ＣＡＡＩ Ｔｒａｎｓ⁃ ａｃｔｉｏｎｓ ｏｎ Ｉｎｔｅｌｌｉｇｅｎｔ Ｓｙｓｔｅｍｓ， ２０１０， ５（５）： ４４３⁃４４７． ［３］赵百轶，张利军，贾鹤鸣．基于四叉树和改进蚁群算法的 全局路径规划［Ｊ］．应用科技， ２０１１， ３８（１０）： ２３⁃２８． ＺＨＡＯ Ｂａｉｙｉ， ＺＨＡＮＧ Ｌｉｊｕｎ， ＪＩＡ Ｈｅｍｉｎｇ． Ｇｌｏｂａｌ ｐａｔｈ ｐｌａｎｎｉｎｇ ｂａｓｅｄ ｏｎ ｑｕａｄｔｒｅｅ ａｎｄ ｉｍｐｒｏｖｅｄ ａｎｔ ｃｏｌｏｎｙ ｏｐｔｉｍｉ⁃ ｚａｔｉｏｎ ａｌｇｏｒｉｔｈｍ ［ Ｊ ］． Ａｐｐｌｉｅｄ Ｓｃｉｅｎｃｅ ａｎｄ Ｔｅｃｈｎｏｌｏｇｙ， ２０１１， ３８（１０）： ２３⁃２８． ［４］ＳＵＮ Ｊｕｎ， ＸＵ Ｗｅｎｂｏ， ＦＥＮＧ Ｂｉｎ． Ａ ｇｌｏｂａｌ ｓｅａｒｃｈ ｓｔｒａｔｅｇｙ ｏｆ ｑｕａｎｔｕｍ⁃ｂｅｈａｖｅｄ ｐａｒｔｉｃｌｅ ｓｗａｒｍ ｏｐｔｉｍｉｚａｔｉｏｎ［Ｃ］ ／ ／ Ｐｒｏ⁃ ｃｅｅｄｉｎｇｓ ｏｆ ｔｈｅ ＩＥＥＥ Ｃｏｎｆｅｒｅｎｃｅ ｏｎ Ｃｙｂｅｒｎｅｔｉｃｓ ａｎｄ Ｉｎｔｅｌｌｉ⁃ ｇｅｎｔ Ｓｙｓｔｅｍｓ． Ｓｉｎｇａｐｏｒｅ， ２００４： １１１⁃１１６． ［５］ ＳＵＮ Ｊｕｎ， ＦＡＮＧ Ｗｅｉ， ＷＵ Ｘｉａｏｊｕｎ， ｅｔ ａｌ． Ｑｕａｎｔｕｍ⁃ｂｅ⁃ ｈａｖｅｄ ｐａｒｔｉｃｌｅ ｓｗａｒｍ ｏｐｔｉｍｉｚａｔｉｏｎ： ａｎａｌｙｓｉｓ ｏｆ ｔｈｅ ｉｎｄｉｖｉｄｕａｌ ｐａｒｔｉｃｌｅ＇ｓ ｂｅｈａｖｉｏｒ ａｎｄ ｐａｒａｍｅｔｅｒ ｓｅｌｅｃｔｉｏｎ［Ｊ］． Ｅｖｏｌｕｔｉｏｎａｒｙ Ｃｏｍｐｕｔａｔｉｏｎ， ２０１２， ２０（３）： ３４９⁃３９３． ［６］ ＣＨＡＩ Ｚｈｉｌｅｉ， ＳＵＮ Ｊｕｎ， ＣＡＩ Ｒｕｉ， ｅｔ ａｌ． Ｉｍｐｌｅｍｅｎｔｉｎｇ ｑｕａｎｔｕｍ⁃ｂｅｈａｖｅｄ ｐａｒｔｉｃｌｅ ｓｗａｒｍ ｏｐｔｉｍｉｚａｔｉｏｎ ａｌｇｏｒｉｔｈｍ ｉｎ ＦＰＧＡ ｆｏｒ ｅｍｂｅｄｄｅｄ ｒｅａｌ⁃ｔｉｍｅ ａｐｐｌｉｃａｔｉｏｎｓ［Ｃ］ ／ ／ Ｐｒｏｃｅｅｄ⁃ ｉｎｇｓ ｏｆ ｔｈｅ ２００９ Ｆｏｕｒｔｈ Ｉｎｔｅｒｎａｔｉｏｎａｌ Ｃｏｍｐｕｔｅｒ Ｓｃｉｅｎｃｅｓ ａｎｄ Ｃｏｎｖｅｒｇｅｎｃｅ Ｉｎｆｏｒｍａｔｉｏｎ Ｔｅｃｈｎｏｌｏｇｙ． Ｗａｓｈｉｎｇｔｏｎ， ＤＣ， ＵＳＡ： ＩＥＥＥ Ｃｏｍｐｕｔｅｒ Ｓｏｃｉｅｔｙ， ２００９： ８８６⁃８９０． ［７］申浩，田峰敏，赵玉新．基于 ＶｏｒｏｎｏｉＣｅｌｌｓ 插值的三维海底 地形图生成方法［Ｊ］．系统仿真学报， ２００６， １８（２）： ４４４⁃ ４４６． ＳＨＥＮ Ｈａｏ， ＴＩＡＮ Ｆｅｎｇｍｉｎ， ＺＨＡＯ Ｙｕｘｉｎ． Ｍｅｔｈｏｄ ｆｏｒ ｇｅｎ⁃ ｅｒａｔｉｎｇ ３Ｄ ｄｉｇｉｔａｌ ｍａｐ ｂａｓｅｄ ｕｐｏｎ ＶｏｒｏｎｏｉＣｅｌｌｓ［Ｊ］． Ｊｏｕｒｎａｌ ｏｆ Ｓｙｓｔｅｍ Ｓｉｍｕｌａｔｉｏｎ， ２００６， １８（２）： ４４４⁃４４６． ［８］姜辉．水下潜器路径规划仿真平台的设计与实现［Ｄ］．哈 尔滨：哈尔滨工程大学， ２００９． ＪＩＡＮＧ Ｈｕｉ． Ｄｅｓｉｇｎ ａｎｄ ｉｍｐｌｅｍｅｎｔａｔｉｏｎ ｏｆ ｔｈｅ ｓｉｍｕｌａｔｉｏｎ ｐｌａｔｆｏｒｍ ｆｏｒ ｕｎｄｅｒｗａｔｅｒ ｖｅｈｉｃｌｅ ｐａｔｈ ｐｌａｎｎｉｎｇ［Ｄ］． Ｈａｒｂｉｎ： Ｈａｒｂｉｎ Ｅｎｇｉｎｅｅｒｉｎｇ Ｕｎｉｖｅｒｓｉｔｙ， ２００９． ［９］梁俊，王琦，刘坤良，等．基于随机中点位移法的三维地形 模拟［Ｊ］．计算机仿真， ２００５， ２２（１）： ２１３⁃２１５． ＬＩＡＮＧ Ｊｕｎ， ＷＡＮＧ Ｑｉ， ＬＩＵ Ｋｕｎｌｉａｎｇ， ｅｔ ａｌ． ３Ｄ ｔｅｒｒａｉｎ ｓｉｍｕｌａｔｉｏｎ ｂａｓｅｄ ｏｎ ｔｈｅ ｍｅｔｈｏｄ ｏｆ ｒａｎｄｏｍ ｍｉｄ⁃ｐｏｉｎｔ ｄｉｓ⁃ ｐｌａｃｅｍｅｎｔ［Ｊ］． Ｃｏｍｐｕｔｅｒ Ｓｉｍｕｌａｔｉｏｎ， ２００５， ２２（ １）： ２１３⁃ ２１５． ［１０］毛宇峰，庞永杰．改进粒子群算法在水下机器人路径规 划中的应用［Ｊ］．计算机应用， ２０１０， ３０（３）： ７８９⁃７９２． ＭＡＯ Ｙｕｆｅｎｇ， ＰＡＮＧ Ｙｏｎｇｊｉｅ． Ａｐｐｌｉｃａｔｉｏｎ ｏｆ ｉｍｐｒｏｖｅｄ ｐａｒｔｉｃｌｅ ｓｗａｍ ｏｐｔｉｍｉｚａｔｉｏｎ ｉｎ ｐａｔｈ ｐｌａｎｎｉｎｇ ｏｆ ｕｎｄｅｒｗａｔｅｒ ｖｅｈｉｃｌｅｓ［Ｊ］． Ｊｏｕｒｎａｌ ｏｆ Ｃｏｍｐｕｔｅｒ Ａｐｐｌｉｃａｔｉｏｎｓ， ２０１０， ３０ （３）： ７８９⁃７９２． ［１１］ＶＡＮ ＤＥＮ ＢＥＲＧＨ Ｆ， ＥＮＧＥＬＢＲＥＣＨＴ Ａ Ｐ． Ａ ｎｅｗ ｌｏｃａｌ⁃ ｌｙ ｃｏｎｖｅｒｇｅｎｔ ｐａｒｔｉｃｌｅ ｓｗａｒｍ ｏｐｔｉｍｉｚｅｒ［Ｃ］ ／ ／ ＩＥＥＥ Ｉｎｔｅｒｎａ⁃ ｔｉｏｎａｌ Ｃｏｎｆｅｒｅｎｃｅ ｏｎ Ｓｙｓｔｅｍｓ， Ｍａｎ ａｎｄ Ｃｙｂｅｒｎｅｔｉｃｓ． Ｈａｍ⁃ ｍａｍｅｔ， Ｔｕｎｉｓｉａ， ２００２， ３： ９４⁃９９． ［１２］ ＷＡＲＲＥＮ Ｃ Ｗ． Ａ ｔｅｃｈｎｉｑｕｅ ｆｏｒ ａｕｔｏｎｏｍｏｕｓ ｕｎｄｅｒｗａｔｅｒ ｖｅｈｉｃｌｅ ｒｏｕｔｅ ｐｌａｎｎｉｎｇ［Ｊ］． ＩＥＥＥ Ｊｏｕｒｎａｌ ｏｆ Ｏｃｅａｎｉｃ Ｅｎｇｉ⁃ ｎｅｅｒｉｎｇ， １９９０， １５（３）： １９９⁃２０４． ［１３］ＶＡＳＵＤＥＶＡＮ Ｃ， ＧＡＮＥＳＡＮ Ｌ． Ｃａｓｅ⁃ｂａｓｅｄ ｐａｔｈ ｐｌａｎｎｉｎｇ ｆｏｒ ａｕｔｏｎｏｍｏｕｓ ｕｎｄｅｒｗａｔｅｒ ｖｅｈｉｃｌｅｓ ［ Ｊ］． Ａｕｔｏｎｏｍｏｕｓ Ｒｏ⁃ ｂｏｔｓ， １９９６， ３（２）： ７９⁃８９． 作者简介： 邹梅魁，男，１９８８ 年生，硕士研究 生，主要研究方向为水下潜器三维路径 规划． ·２２４· 智 能 系 统 学 报 第 ８ 卷

第3期 邹梅魁，等：采用量子粒子群算法的潜器路径规划 ·225· 于飞，男，1974年生，教授，博士生 吕重阳，男，1987年生，硕士研究 导师，国家自然科学基金同行评议专 生，主要研究方向为群智能算法. 家主要研究方向为惯性测量、组合导 航数据融合、潜器导航等.作为负责人 主持国家自然科学基金1项、教育部博 士点基金1项，获黑龙江省教学成果奖 2项.发表学术论文30余篇，其中被SCI检索4篇、EI检索 18篇，申请国家发明专利1项. 2013第6届计算智能与设计国际会议(ISCID2013) 2013 6th International Symposium on Computational Intelligence and Design Dear colleagues and friends 2013 6th International Symposium on Computational Intelligence and Design(ISCID2013)will take place in Hangzhou, China,between 28-29 October,2013.This symposium provides an idea-exchange and discussion platform for the world 's engineers and academia to share cutting-edge information,address the hottest issue in computational intelligence and de- sign,explore new technologies,exchange and build upon ideas.We're certain you will find the city of Hangzhou and the surrounding area to be most pleasant and it will be our distinct pleasure to welcome each of you to the ISCID in October 2013. Publication The proceedings of ISCID2013 will be published by IEEE Computer Society Conference Service Publishing (CPS),and indexed by EI.All proceedings of ISCID2008-2012 have been indexed by EI,and included in the digital libraries (CS- DL.IEEE Xplore,IEEE IEL). Sponsors Zhejiang University,China University of Bristol,UK IEEE Nanjing Compuational Intelligence Chapter (Technical co-sponsor) Tsinghua University,China Zhejiang Sci-Tech University,China Important dates Deadline for paper submission:June 11 (extended to)July 1,2013 Notification of acceptance/rejection:July 8,2013 Camera-ready and early registration:July 15,2013 Conference:28-29 October,2013 Contact person If you have any inquiries regarding registration or your registration status,please contact Linna Zhu (Zhejiang University,China) Affiliation:College of Computer Science at Zhejiang University,Hangzhou,China Phone:+86-15068186792 E-mail:iscid2013@gmail.com Website:http://iukm.zju.edu.cn/iscid/index.html

于飞，男，１９７４ 年生，教授，博士生 导师，国家自然科学基金同行评议专 家．主要研究方向为惯性测量、组合导 航数据融合、潜器导航等．作为负责人 主持国家自然科学基金 １ 项、教育部博 士点基金 １ 项，获黑龙江省教学成果奖 ２ 项．发表学术论文 ３０ 余篇，其中被 ＳＣＩ 检索 ４ 篇、ＥＩ 检索 １８ 篇，申请国家发明专利 １ 项． 吕重阳，男，１９８７ 年生，硕士研究 生，主要研究方向为群智能算法． ２０１３ 第 ６ 届计算智能与设计国际会议（ ＩＳＣＩＤ２０１３） ２０１３ ６ｔｈ Ｉｎｔｅｒｎａｔｉｏｎａｌ Ｓｙｍｐｏｓｉｕｍ ｏｎ Ｃｏｍｐｕｔａｔｉｏｎａｌ Ｉｎｔｅｌｌｉｇｅｎｃｅ ａｎｄ Ｄｅｓｉｇｎ Ｄｅａｒ ｃｏｌｌｅａｇｕｅｓ ａｎｄ ｆｒｉｅｎｄｓ ２０１３ ６ｔｈ Ｉｎｔｅｒｎａｔｉｏｎａｌ Ｓｙｍｐｏｓｉｕｍ ｏｎ Ｃｏｍｐｕｔａｔｉｏｎａｌ Ｉｎｔｅｌｌｉｇｅｎｃｅ ａｎｄ Ｄｅｓｉｇｎ （ＩＳＣＩＤ２０１３） ｗｉｌｌ ｔａｋｅ ｐｌａｃｅ ｉｎ Ｈａｎｇｚｈｏｕ， Ｃｈｉｎａ， ｂｅｔｗｅｅｎ ２８—２９ Ｏｃｔｏｂｅｒ， ２０１３． Ｔｈｉｓ ｓｙｍｐｏｓｉｕｍ ｐｒｏｖｉｄｅｓ ａｎ ｉｄｅａ⁃ｅｘｃｈａｎｇｅ ａｎｄ ｄｉｓｃｕｓｓｉｏｎ ｐｌａｔｆｏｒｍ ｆｏｒ ｔｈｅ ｗｏｒｌｄ ＇ｓ ｅｎｇｉｎｅｅｒｓ ａｎｄ ａｃａｄｅｍｉａ ｔｏ ｓｈａｒｅ ｃｕｔｔｉｎｇ⁃ｅｄｇｅ ｉｎｆｏｒｍａｔｉｏｎ， ａｄｄｒｅｓｓ ｔｈｅ ｈｏｔｔｅｓｔ ｉｓｓｕｅ ｉｎ ｃｏｍｐｕｔａｔｉｏｎａｌ ｉｎｔｅｌｌｉｇｅｎｃｅ ａｎｄ ｄｅ⁃ ｓｉｇｎ， ｅｘｐｌｏｒｅ ｎｅｗ ｔｅｃｈｎｏｌｏｇｉｅｓ， ｅｘｃｈａｎｇｅ ａｎｄ ｂｕｉｌｄ ｕｐｏｎ ｉｄｅａｓ． Ｗｅ＇ｒｅ ｃｅｒｔａｉｎ ｙｏｕ ｗｉｌｌ ｆｉｎｄ ｔｈｅ ｃｉｔｙ ｏｆ Ｈａｎｇｚｈｏｕ ａｎｄ ｔｈｅ ｓｕｒｒｏｕｎｄｉｎｇ ａｒｅａ ｔｏ ｂｅ ｍｏｓｔ ｐｌｅａｓａｎｔ ａｎｄ ｉｔ ｗｉｌｌ ｂｅ ｏｕｒ ｄｉｓｔｉｎｃｔ ｐｌｅａｓｕｒｅ ｔｏ ｗｅｌｃｏｍｅ ｅａｃｈ ｏｆ ｙｏｕ ｔｏ ｔｈｅ ＩＳＣＩＤ ｉｎ Ｏｃｔｏｂｅｒ ２０１３． Ｐｕｂｌｉｃａｔｉｏｎ Ｔｈｅ ｐｒｏｃｅｅｄｉｎｇｓ ｏｆ ＩＳＣＩＤ２０１３ ｗｉｌｌ ｂｅ ｐｕｂｌｉｓｈｅｄ ｂｙ ＩＥＥＥ Ｃｏｍｐｕｔｅｒ Ｓｏｃｉｅｔｙ Ｃｏｎｆｅｒｅｎｃｅ Ｓｅｒｖｉｃｅ Ｐｕｂｌｉｓｈｉｎｇ （ＣＰＳ）， ａｎｄ ｉｎｄｅｘｅｄ ｂｙ ＥＩ． Ａｌｌ ｐｒｏｃｅｅｄｉｎｇｓ ｏｆ ＩＳＣＩＤ２００８—２０１２ ｈａｖｅ ｂｅｅｎ ｉｎｄｅｘｅｄ ｂｙ ＥＩ， ａｎｄ ｉｎｃｌｕｄｅｄ ｉｎ ｔｈｅ ｄｉｇｉｔａｌ ｌｉｂｒａｒｉｅｓ （ＣＳ⁃ ＤＬ， ＩＥＥＥ Ｘｐｌｏｒｅ， ＩＥＥＥ ＩＥＬ）． Ｓｐｏｎｓｏｒｓ Ｚｈｅｊｉａｎｇ Ｕｎｉｖｅｒｓｉｔｙ， Ｃｈｉｎａ Ｕｎｉｖｅｒｓｉｔｙ ｏｆ Ｂｒｉｓｔｏｌ， ＵＫ ＩＥＥＥ Ｎａｎｊｉｎｇ Ｃｏｍｐｕａｔｉｏｎａｌ Ｉｎｔｅｌｌｉｇｅｎｃｅ Ｃｈａｐｔｅｒ （Ｔｅｃｈｎｉｃａｌ ｃｏ⁃ｓｐｏｎｓｏｒ） Ｔｓｉｎｇｈｕａ Ｕｎｉｖｅｒｓｉｔｙ， Ｃｈｉｎａ Ｚｈｅｊｉａｎｇ Ｓｃｉ⁃Ｔｅｃｈ Ｕｎｉｖｅｒｓｉｔｙ， Ｃｈｉｎａ Ｉｍｐｏｒｔａｎｔ ｄａｔｅｓ Ｄｅａｄｌｉｎｅ ｆｏｒ ｐａｐｅｒ ｓｕｂｍｉｓｓｉｏｎ： Ｊｕｎｅ １１ （ｅｘｔｅｎｄｅｄ ｔｏ） Ｊｕｌｙ １， ２０１３ Ｎｏｔｉｆｉｃａｔｉｏｎ ｏｆ ａｃｃｅｐｔａｎｃｅ ／ ｒｅｊｅｃｔｉｏｎ： Ｊｕｌｙ ８， ２０１３ Ｃａｍｅｒａ⁃ｒｅａｄｙ ａｎｄ ｅａｒｌｙ ｒｅｇｉｓｔｒａｔｉｏｎ： Ｊｕｌｙ １５， ２０１３ Ｃｏｎｆｅｒｅｎｃｅ： ２８—２９ Ｏｃｔｏｂｅｒ， ２０１３ Ｃｏｎｔａｃｔ ｐｅｒｓｏｎ Ｉｆ ｙｏｕ ｈａｖｅ ａｎｙ ｉｎｑｕｉｒｉｅｓ ｒｅｇａｒｄｉｎｇ ｒｅｇｉｓｔｒａｔｉｏｎ ｏｒ ｙｏｕｒ ｒｅｇｉｓｔｒａｔｉｏｎ ｓｔａｔｕｓ， ｐｌｅａｓｅ ｃｏｎｔａｃｔ Ｌｉｎｎａ Ｚｈｕ （Ｚｈｅｊｉａｎｇ Ｕｎｉｖｅｒｓｉｔｙ， Ｃｈｉｎａ） Ａｆｆｉｌｉａｔｉｏｎ： Ｃｏｌｌｅｇｅ ｏｆ Ｃｏｍｐｕｔｅｒ Ｓｃｉｅｎｃｅ ａｔ Ｚｈｅｊｉａｎｇ Ｕｎｉｖｅｒｓｉｔｙ， Ｈａｎｇｚｈｏｕ， Ｃｈｉｎａ Ｐｈｏｎｅ： ＋８６⁃１５０６８１８６７９２ Ｅ⁃ｍａｉｌ： ｉｓｃｉｄ２０１３＠ ｇｍａｉｌ．ｃｏｍ Ｗｅｂｓｉｔｅ： ｈｔｔｐ： ／ ／ ｉｕｋｍ．ｚｊｕ．ｅｄｕ．ｃｎ ／ ｉｓｃｉｄ ／ ｉｎｄｅｘ．ｈｔｍｌ 第 ３ 期 邹梅魁，等：采用量子粒子群算法的潜器路径规划 ·２２５·