
第8卷第2期 智能系统学报 Vol.8 No.2 2013年4月 CAAI Transactions on Intelligent Systems Apr.2013 D0I:10.3969/i.issn.16734785.201208022 网络出版t地址:htp://www.cnki.net/kcma/detail/23.1538.TP.20130409.1436.006.html 复杂环境下多机器人觅食路径规划与控制 杨茂1,田彦涛2 (1.东北电力大学电气工程学院,吉林吉林132012:2.吉林大学通信工程学院,吉林长春130025) 摘要:针对多机器人系统领域中复杂环境下的稳定协同觅食问题,利用粒子群优化算法规划出多机器人中心位置 在相应目标下的最优光滑路径.在此基础上设计了相应的分布式控制策略,并对该控制策略下多机器人系统运动的 稳定性和内聚性进行了分析,证明了群体内部平均动能能够收敛至给定值,进而保证了多机器人系统运动规模的可 控性,且不发生碰撞.仿真试验结果表明,在该控制策略下,多机器人系统能够在复杂的环境下有效地实现稳定觅食 行为. 关键词:多机器人:分布式控制;觅食;路径规划;内聚性 中图分类号:TP18文献标志码:A文章编号:16734785(2013)02016206 Foraging path planning and control for multi-robot in complex environment YANG Mao',TIAN Yantao2 (1.Electrical Engineering College,Northeast Dianli University,Jilin 132012,China;2.School of Communication Engineering,Jilin University,Changchun 130025,China) Abstract:Aiming at the stable cooperative foraging problems of the multi-robot system in complex environments, the Particle Swarm Optimization (PSO)algorithm was adopted in this paper to plan an optimal smooth path of the center of multi-robot system in corresponding objects.In order to plan an optimal smooth path of the center of multi- robot system in corresponding objects,it was necessary to examine the system in great detail.And on this basis,a corresponding distributed controller was designed,and a stabilization and cohesion analysis of the multi-robot mov- ing was performed.The control strategy,proved the swarm internal average kinetic energy did converge to the given value,and the multi-robot system moving scale was under control,indicating no collisions.Experiments have been completed and verified the designed controller.The results show that the proposed controller enables the multi-robot system to reach a stable foraging behavior in complex environments. Keywords:multi-robot;decentralized control;foraging;path planning;cohesion 群体觅食行为是自然界中常见现象之一,与个性)的条件下建立了多机器人系统群体觅食的宏观 体独立觅食相比较,群体觅食行为可以获得更大的 数学模型.在微观方面以系统中个体的受力及状态 生存几率及更高的效率.多机器人系统的研究受自 为研究对象,例如Tanner等io从控制理论的角度 然界中群体智能行为的启发,并取得了丰富的研究 对自然界中的集群现象做出了理论解释,并运用代 成果1.为了描述群体觅食任务,研究人员分别从 数图论、非光滑分析等数学工具提出了一类基于局 宏观和微观2个方面建立了数学模型.在宏观方面 部信息交互的分布式控制策略,并证明了在此控制 以特定状态下机器人的数量或密度为研究对象,例 策略下群体速度收敛到同一值.Olfati-Saber等采 如Lerman等9]在满足马尔可夫性(或半马尔可夫 用了平滑的势能函数,提出了一个局部控制策略使 得群体形成稳定的集群运动.Gai等2建立了基于 收稿日期:2012-0816.网络出版日期:20130409. 个体的连续时间群体聚集模型,并分析了控制策略 基金项目:东北电力大学博土基金资助项目(BSXM-201016) 通信作者:杨茂.E-mail:yangmao820@yahoo.com.cm. 下系统的稳定性,群体在有限的时间内实现收敛,并

第2期 杨茂,等:复杂环境下多机器人觅食路径规划与控制 ·163 给出了基于模型参数的内聚性分析.Li等3]考虑 首先将机器人运动空间离散化,采用三次样条 了噪声环境下多机器人系统的稳定觅食控制策略。 曲线作为基本参考轨迹,将基本参考轨迹依次按一 但以上问题的研究都是在外部环境相对简单的基础 定规律连接起来构成最终的参考轨迹, 上展开的. 因此,在二维空间中,路径规划问题可以看作三次 针对于复杂环境下的多机器人系统觅食任务, 样条空间中搜索最优参数所对应的参考轨迹问题 本文从路径规划及内聚性控制2个方面进行了研 这里采用Ferguson样条作为基本参考轨迹,即 究,首先利用粒子群优化算法规划出安全且高效的 r(t)=(x(),y(t))= 光滑路径,在此基础上使群体中心跟踪该路径,并设 Pafi (t)+Pf (t)+Pafs (t)+Pifa (t). 计基于内部平均动能的分布式控制策略保证群体的 式中:Po、P、P、P1为样条参数向量,f(t)f(t)、 内聚性,来实现避障.最后利用仿真试验验证上述控 f方(t)f()为三次多项式 制策略的可行性。 2个基本样条连接时要求前一个样条的终点及 其切向量等于其相连接样条的起点及其切向量。 1路径规划 f(t)=2e3-3t2+1, 路径规划是移动机器人系统研究的主要问题之 f5(t)=-23+3t, 一.觅食任务实际上是多机器人系统的一种路径规 6(t)=e3-22+t, 划问题. f(t)=e-. 1.1任务描述 此时待优化样条系数构成粒子,其结构如图1所示. 觅食任务可以表述为多机器人系统利用分布式 感知能力及数量优势,从指定的初始位置到达指定 的最终位置,避开环境中的障碍物,实现安全可靠的 Po时 觅食行为策略.为了保证多机器人系统中所有个体 运动的安全性,需要事先进行群体中心位置的路径 图1粒子的结构 规划 Fig.1 The structure of the particles 1.2基于粒子群优化算法的路径规划 适应度函数的设置考虑2个方面,一方面是要 粒子群优化算法(particle swarm optimization, 求机器人运动的安全性:令D为安全距离,其设置 PS0)是一种经典的智能优化算法,其思想源于对鸟 方式在后面分布式控制中有具体说明. 类捕食行为的研究.在PS0算法中,可行域中的每 r1,Dafe<dmin 个可行解为一个粒子,每个粒子都对应一个适应值。 f= 首先初始化种群,每个粒子在解空间中运动,并经过 特定的迭代算法搜索最优解.标准的粒子群优化算 式中:d=V(0-0,)+G0-o,产,0为 法数学表示如下. 障碍物集合.另一方面要求距离最短化, 设解空间的维数为D,粒子的个数为n,第i个 =l/lmin 粒子位置表示为X=[,…,],第i个粒子到 式中:l血为欧式空间中起点和终点的直线距离, 目前为止搜索到的最优位置为P:=[PP,…P], 1=0√xo))+(y)d. 整个粒子群到目前为止搜索到的最优位置为P。= 最终的适应度函数f定义为f=+f: [PsPa…Psn小,第i个粒子的速度为V:= [VV,…V,].每个粒子的速度和位置按如下公式 2 数学模型 进行更新: 2.1个体数学模型 V,(t+1)=wy()+cr(t)(P。- 假设1多机器人之间的通信不存在时滞,每 xn)+c23(t)(Pn-,), 个机器人为质点, X,(t+1)=x()+V(t+1), 考虑在二维空间中,多机器人系统由N个个体 1≤i≤n,1≤d≤D. 组成,假设每个个体的质量为m·个体的位置表示 式中:9为加速系数,(),3()~V(0,1)为 为x=[x好],i=1,2,…,N,则个体的速度为v= 惯性权重,山是用来平衡搜索与利用之间的关系, []=[]

·164 智能系统学报 第8卷 对于群体中的每个个体,其数学模型为 式中: [=v, lm,=4:-bw. 为了分析系统运动的稳定性及安全距离,需定 义群体中心. 定义1群体的中心位置和平均速度定义为 =(三)-[()r-6 x=立mx/∑mp=m/召m 3分布式控制器设计及系统分析 特别地,对于同构机器人,有m:=m,故有 N 3.1稳定性分析 x= N,=宫N 在多机器人觅食过程中,利用粒子群优化算法 2.2群体系统能量分类 规划出群体中心的轨迹,只能够实现群体中心的避 在多机器人系统中可以将能量划分为多种形 障.为了保证多机器人系统中每个个体均不发生碰 式,例如群体吸引排斥势能、群体总的动能和群体平 撞(包括机器人之间的避障以及机器人和障碍物之 均动能等,群体吸引排斥势能的形式为 间的避障),还应对群体规模实现有效地控制,故提 N-N 出基于群体温度的分布式控制策略为 J(x)= 名A(-I)-(Ix-I u=-k(x-xa)-ka(衣-a)+ (1) 式中:x:为前一部分中利用PS0算法规划出来的群 式中:J。和J,分别为吸引势能和排斥势能.并假设 体中心轨迹,4=-28,(少-). 存在函数g.(‖x-x‖)和g,(‖x-x‖)使得 7J(‖x-x‖)=g.(x-),7J,(x-x)= A,=任-+ ‖y-pJ2 g,(x-x)成立. (A-bwM=2:2, 假设2存在一个正数8>0: Iv-v‖2 g.(lx-xI)≥g,(lx-xI), Pg=g(‖x-x‖)-g,(‖x-xl). ‖x-x‖≥6, 定理1阻尼环境下,设计分布式控制器4: g(lx-x1)≤g,(lx-xI), 4=-k(d-)-k(e-xa)+(4+4)-b加 ‖x-x‖≤6, 式中:”=P,则在任意初始状态下,多机器人系统 g(‖x-xI)=g,(‖x-xI), 可以在期望的群体温度下实现稳定觅食任务, x-x‖=6, 证明由于 群体总的动能为E,()宫m)。 群体平均动能为E,)=名m)151 N-1 N - 高AA,(-+a,(w-】=0 定义2群体的内部能量定义为 故可以视为中的一部分,故有 U(x,v)=[J(x)+E(v)-E(y)]/N.(3) u=-k()-ka(). 定义3群体温度定义为T=[E.(v)- 进而 E()]/W. 群体温度是一种特殊的能量形式,刻画了群体 b=六8tg1-(宫1=0. 中的速度分布情况,并能够实现对群体规模的控制。 特别地,还有以下几种等价形式: 。=为宫(4+)w]. )=袋名I1-NII) =N1(宫)-()'%]1 示宫点r1时 (含)-A[w)w], 对群体温度T()关于时间求导有 T()=中+o+. T)=o+中=为宫[(2.+)]}+

第2期 杨茂,等:复杂环境下多机器人觅食路径规划与控制 ·165· A(宫)-宫1 4 仿真试验与分析 8-Ad0-含ar-+ 为了验证上述分布式控制器的效果,在Matlab (2008b)下进行了仿真试验.试验模拟由10个个 (宫)-含(ww] 体组成的多机器人系统在二维空间中运动.其中个 体初始中心位置为(200,200);初始速度在(0,1)内 a-m宫盆-P-+划= N-I N 随机获得;目标中心位置为(1400,1000);障碍物 为7个;学习因子C1=C2=2;样条个数为5个;最 -H[(A-W/N)T-(A-W/NDNy(N-1)/2+]= 大迭代次数为100;迭代步长为0.02;迭代终止精度 为10-6.优化过程如图2~5所示. -a2T-Y(N-1)(b/N-)2. m 1410 也就是T()+A2WT(v)+YN-1)(b/N-2 m 0.显然对于任意的入>0,T()是收敛的,通过y的 选取可以使T()收敛于指定的群体温度值, 3.2内聚性分析 定理2若假设1、2成立,且群体内部能量有 界,即 x/m 6*10 U(x,)≤C, (3) 则群体运动规模有界。 图2机器人的初始中心轨迹 证明 Fig.2 Initial trajectories of robots'center 设h(‖x-x‖)=J.(Ix-xl)-J,(Ix- xI),则由假设2显然可知h(Ix-xI)在‖x- 14r产10 :‖=6时取全局最小值,将式(1)、式(2)代入式 12 (3),可得 10 N-1 N 8/ 名,A[Ir-rI]≤[C-], E 含6 从而可得 4 h(Ix-x‖)+ 名名 4 [h()][N(C-T)] 82610 x/m (1k)*(i》 图3迭代30次后机器人中心轨迹 由假设2可知 Fig.3 Trajectories of robots'center after 30 iterations (12-I】≥2-6 (1,(》 14*10 因此有 12 h(Ix-x‖)≤[N(C-T)] 0.5(N2-N-3)h(6) 成立. 三6 由假设2及隐函数定理可得 Ix-x‖≤h4{[N(C-T)] 0.5(N2-N-3)h(6), x/m 即群体规模有界. 图4迭代80次后机器人中心轨迹 Fig.4 Trajectories of robots'center after 80 iterations
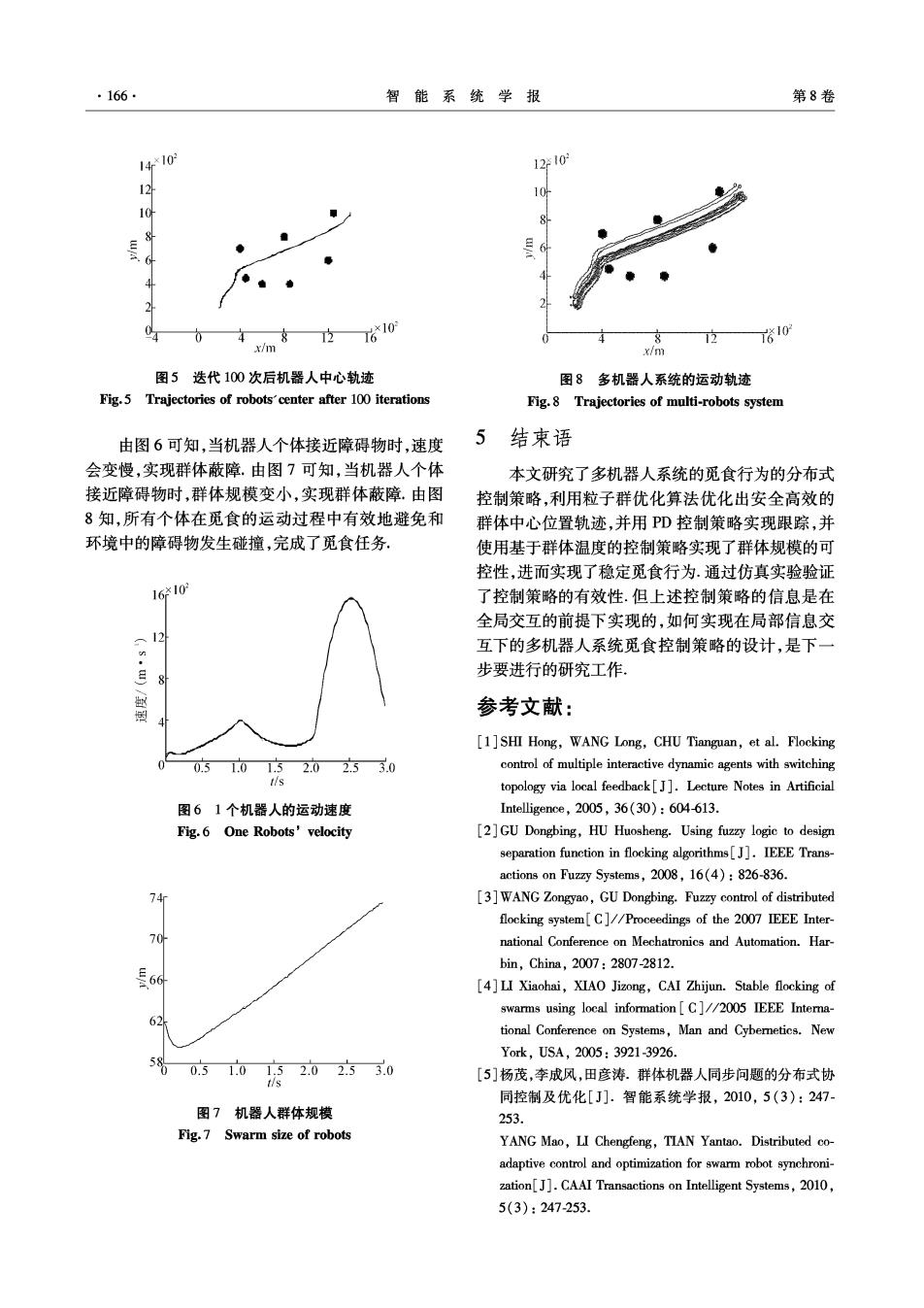
·166 智能系统学报 第8卷 *10 12ě102 10 10 4 8 12 7610 x/m 12610 x/m 图5迭代100次后机器人中心轨迹 图8多机器人系统的运动轨迹 Fig.5 Trajectories of robots center after 100 iterations Fig.8 Trajectories of multi-robots system 由图6可知,当机器人个体接近障碍物时,速度 5结束语 会变慢,实现群体蔽障.由图7可知,当机器人个体 本文研究了多机器人系统的觅食行为的分布式 接近障碍物时,群体规模变小,实现群体蔽障。由图 控制策略,利用粒子群优化算法优化出安全高效的 8知,所有个体在觅食的运动过程中有效地避免和 群体中心位置轨迹,并用PD控制策略实现跟踪,并 环境中的障碍物发生碰撞,完成了觅食任务。 使用基于群体温度的控制策略实现了群体规模的可 控性,进而实现了稳定觅食行为.通过仿真实验验证 16×10 了控制策略的有效性.但上述控制策略的信息是在 全局交互的前提下实现的,如何实现在局部信息交 12 互下的多机器人系统觅食控制策略的设计,是下一 步要进行的研究工作。 参考文献: [1]SHI Hong,WANG Long,CHU Tianguan,et al.Flocking 00.51.01.52.02.53.0 control of multiple interactive dynamic agents with switching s topology via local feedback[].Lecture Notes in Artificial 图61个机器人的运动速度 Intelligence,2005,36(30):604-613. Fig.6 One Robots'velocity [2]GU Dongbing,HU Huosheng.Using fuzzy logic to design separation function in flocking algorithms[J].IEEE Trans- actions on Fuzzy Systems,2008,16(4):826-836. 74 [3]WANG Zongyao,GU Dongbing.Fuzzy control of distributed flocking system[C]//Proceedings of the 2007 IEEE Inter- 70 national Conference on Mechatronics and Automation.Har- bin,China,2007:2807-2812. 366 [4]LI Xiaohai,XIAO Jizong,CAI Zhijun.Stable flocking of swarms using local information [C]//2005 IEEE Intera- 62 tional Conference on Systems,Man and Cybernetics.New York,USA,2005:39213926. 5%0内10府202本30 [5]杨茂,李成风,田彦祷.群体机器人同步问题的分布式协 同控制及优化[J].智能系统学报,2010,5(3):247- 图7机器人群体规模 253. Fig.7 Swarm size of robots YANG Mao,LI Chengfeng,TIAN Yantao.Distributed co- adaptive control and optimization for swarm robot synchroni- zation[J].CAAI Transactions on Intelligent Systems,2010, 5(3):247-253

第2期 杨茂,等:复杂环境下多机器人觅食路径规划与控制 ·167· [6]吴宪祥,郭宝龙,王娟.基于粒子群三次样条优化的移动 [13]LIU Yanfei,PASSINO K M.Stable social foraging swarms 机器人路径规划算法[J].机器人,2009,31(6):556 in a noisy environment[J].IEEE Transactions on Auto- 570. matic Control,2004,49(1):30-44. WU Xianxiang,GUO Baolong,WANG Juan.Mobile robot 作者简介: path planning algorithm based on particle swarm optimization 杨茂,男,1982年生,讲师,博士.主 of cubic splines[J].Robot,2009,31(6):556-570. 要研究方向为群体机器人系统、风电功 [7]JADBABIE A,LIN J,MORSE A S.Coordination of groups 率预测. of mobile autonomous agents using nearest neighborhood rules[J].IEEE Transactions on Automatic Control,2003, 48(6):988-1001. [8]PEDRAMI R,GORDON B W.Temperature control of ener- getic swarms C]//Proceedings of the 2007 IEEE Interna- 田彦涛,男,1958年生,教授,博士 tional Conference on Mechatronics and Automation.Harbin, 生导师,博士,中国自动化学会理事、中 China,2007:2639-2644. 国自动化学会机器人专业委员会常务 [9]LERMAN K.MARINOLI A.GALSTYAN A.A review of 委员、吉林省自动化学会理事长、吉林 probabilistic macroscopic models for swarm robotic systems 省通信学会副理事长、吉林省电机工程 [J].Lecture Notes in Computer Science,2005,33(42): 学会常务理事、中科院沈阳自动化研究 143-152. 所先进造技术实验室学术委员会委员、中国自动化学会 [10]TANNER H G,JABABAIE A,PAPPAS G J.Stable floc- 《机器人》学报编委、《吉林大学学报(信息科学版)》副主编 king of mobile agent,part I:fixed topology[C]//Proceed- 主要研究方向为复杂系统建模、优化与控制、分布式智能系 ings of Conference on Decision Control.Maui,Hawaii, 统与网络控制.近5年,完成国家“863”计划项目1项、国家 USA,2003:2010-2015. 自然科学基金项目1项、吉林省科技发展计划项目3项、国 [11]SABER O,MURRAY R M.Consensus seeking in multi-a- 家“863”智能机器人网点实验室基金项目1项;目前,负责 gent systems under dynamically changing interaction topol- 承担国家“863”计划项目和国家自然科学基金项目等国家 ogies[J].IEEE Transactions on Automation and Control, 级科研项目3项、吉林省科技发展计划重点项目3项.发表 2005,50(5):655661. 学术论文70余篇,其中被SCI、EI、ISTP检索36篇. [12]GAZI V,PASSINO K M.Stability analysis of social fora- ging swarm[J].IEEE Transactions on Systems,Man,and Cybernetics-Part B:Cybernetics,2004,34(1):539-557
发表 学术论文70余篇,其中被SCI、EI、ISTP检索36篇