
Lecture:Introduction to Electrodynamics 1.1 Electrostatics Min Chen minchen (@situ.edu.cn Laboratory for Laser Plasma Physics (LLP) Department of Physics Shanghai Jiao Tong University 13-02-25 Only discuss static electric fields.No time evolution of the source charges! 1 Calculate field from existed charge distribution. Learn fundamental knowledge of a vector field
Min Chen minchen@sjtu.edu.cn Laboratory for Laser Plasma Physics (LLP) Department of Physics Shanghai JiaoTong University 13-02-25 1.1 Electrostatics Lecture: Introduction to Electrodynamics Only discuss static electric fields. No time evolution of the source charges! Calculate field from existed charge distribution. Learn fundamental knowledge of a vector field. 1

What is physics? From Phenomenon to theory Daily Experimental observations: Two kinds of charge,force interaction Like charges repel,but opposite charges attract Quantitatively description:Coulomb's law Test particle(q,X),source particle (q',X') 99'x-x' C2 F(x)= 4π0k-x3 80=8.85×1012 N.m2 Direction,Eo permitivity of free space/vacuum permitivity Charge of two particles,their positions(no velocity here!!!Static field). e=1.6×10-19C Calculate the acceleration of two electrons with 2 a distance of 1m? Two-Point-charge interaction
From Phenomenon to theory Daily & Experimental observations: Two kinds of charge, force & interaction Quantitatively description: Coulomb’s law + - Like charges repel, but opposite charges attract Direction, e0 permitivity of free space/ vacuum permitivity Charge of two particles, their positions (no velocity here!!! Static field). Two-Point-charge interaction 2 What is physics? Test particle (q,X), source particle (q’,X’) 2 2 12 0 8.85 10 N m C e e C 19 1.6 10 Calculate the acceleration of two electrons with a distance of 1m?

From Phenomenon to theory For many source particles??? Superposition principle of electric field (Experimental demonstration) The interaction between any two charges is completely unaffected by the presence of others. Just linear superposition. 3
From Phenomenon to theory For many source particles??? Superposition principle of electric field (Experimental demonstration) 3 i i i i X X qq X X F X 3 ' ' ' 4 0 1 ( ) e The interaction between any two charges is completely unaffected by the presence of others. Just linear superposition

Abstract new concept From Force to Field .Field is a really existed matter.Charge and fields are the two main“actors'”in the EM theory. Field can be measured by a test particle.E=F/q Electric field is a vector field. Estaf(x)= g x-x' Static electric field of a point like charge: 4πe0k-x3 Static electric fields of many point like charges: 四高又子 Continuous charge distribution,Charge density,and electric static field E=人w千 4 The field only depends on the source charges.Not the test particle
From Force to Field Field is a really existed matter. Charge and fields are the two main “ actors ” in the EM theory. Field can be measured by a test particle. E=F/q Electric field is a vector field. Continuous charge distribution, Charge density,and electric static field Static electric field of a point like charge: Static electric fields of many point like charges: 4 Abstract new concept The field only depends on the source charges. Not the test particle

What is a field? Football field?Research field? A physical field is a physical variable which distributes in space.It can be a real entity (EM field)or just a kind of description of a motion(temperature field,fluid field).It can be a scalar(温度场),a vector(电磁场、速度场)( or a tensor(张量). .A field usual F(t,x,y,Z,… 1T4 Here we stu a real matter.Td!!t 4,φ) (a) (b) 图1-3温度场(a)和流速场(b) 5 You will know more about fields'properties in this course
What is a field? 5 Football field? Research field? A physical field is a physical variable which distributes in space. It can be a real entity (EM field) or just a kind of description of a motion (temperature field, fluid field). It can be a scalar(温度场), a vector (电磁场、速度场) or a tensor(张量). A field usually is a function of both space and time. F(t,x,y,z,……) Here we study the electromagnetic field, which is a real matter. To describe it we need vectors. (E,B) / (A,f) You will know more about fields’ properties in this course

Definition of three kinds of charge density Volume density do p= Charge per unit volume dxdydz Area density Charge per unit area d№=pd dxdy Linear density 1= Charge per unit length de =ody=pdyd dx Always used in different dimensionalities according to different symmetries. 6
Volume density Charge per unit volume Area density Charge per unit area Linear density Charge per unit length dxdydz dQ dz dxdy dQ dy dydz dx dQ x y z Always used in different dimensionalities according to different symmetries. Definition of three kinds of charge density 6

Calculation of electric static field Example 1 Calculate the electricfield at above the midpoint ofa straight line segment of length 21. which carries a uniform charge ofQ For a long thin straight wire,although it has three dimensionalities,we can use linear charge density to describe the charge distribution when the scale length we study is much larger than their its transverse size. 40 p= + πd21 九= Q/1 十 E(z) 21 0 Z ++ Discuss: l.l→infinite 2.z>>1 E=E.e.= 1 21 4πE0z√z2+12
For a long thin straight wire, although it has three dimensionalities, we can use linear charge density to describe the charge distribution when the scale length we study is much larger than their its transverse size. d Q l d l Q / 4 2 7 Calculation of electric static field + + + + + + + + + + + + E(z) 2l z q Example 1 Calculate the electric field at z above the midpoint of a straight line segment of length 2l, which carries a uniform charge of Q. z z z e z z l l E E e ˆ 2 4 1 ˆ 2 2 0 e Discuss: 1. l infinite 2. z>>l
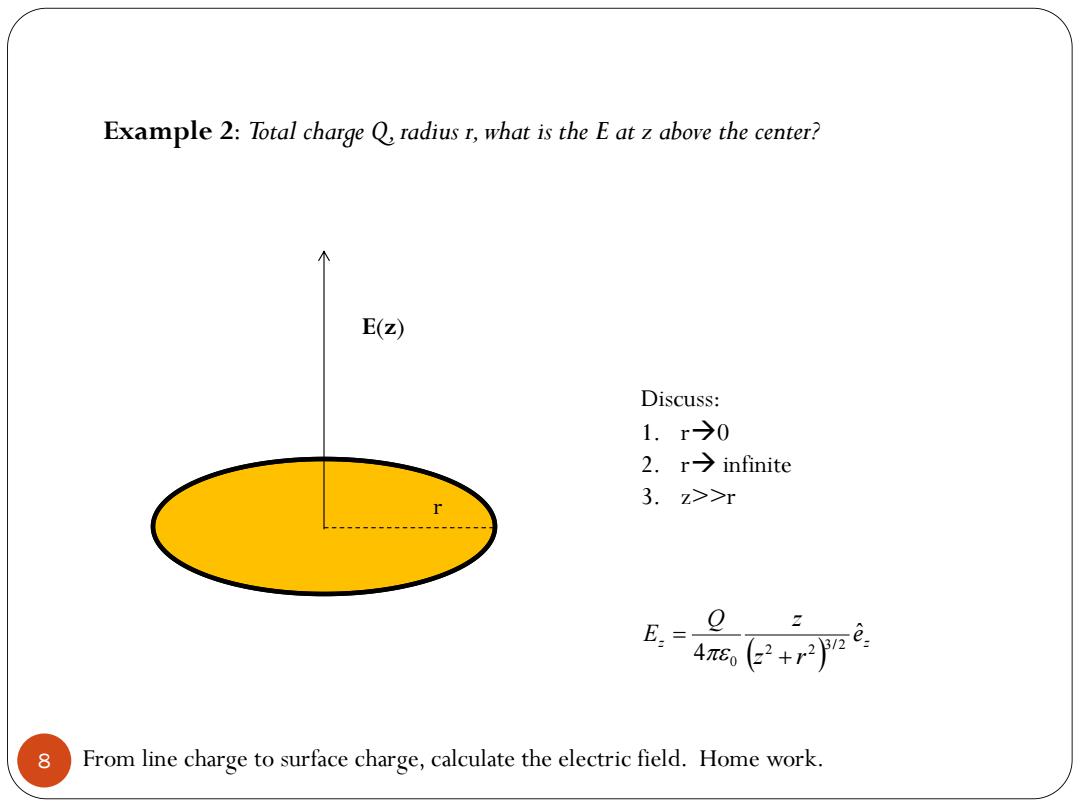
Example 2:Total charge Q radius r,what is the E atz above the center? 个 E(z) Discuss: 1.r→0 2.r→infinite 3.z>>r Q 8 From line charge to surface charge,calculate the electric field.Home work
8 Example 2: Total charge Q,radius r,what is the E at z above the center? r E(z) Discuss: 1. r0 2. r infinite 3. z>>r From line charge to surface charge,calculate the electric field. Home work. z z e z r Q z E ˆ 4 3/ 2 2 2 0 e

Example 3:Infinite Plane Sheet of Charge,surface density of charge. d Divide the plane into slides with width of dx along y direction. dq=oLdx,then the line density is=odx From Ex.1,we know dE=odx/r2To 12l 它=Ee,=460N2+ e. a -c0 o 2 arctan- 三 a 9
9 Example 3: Infinite Plane Sheet of Charge,surface density of charge . Divide the plane into slides with width of dx along y direction. dq= Ldx, then the line density is = dx From Ex.1, we know dE= dx/r2e0 z z z e z z l l E E e ˆ 2 4 1 ˆ 2 2 0 e 0 0 2 2 0 0 2 arctan 1 2 2 sin 2 e e e q e a x a a dx a x a dx r E dEz
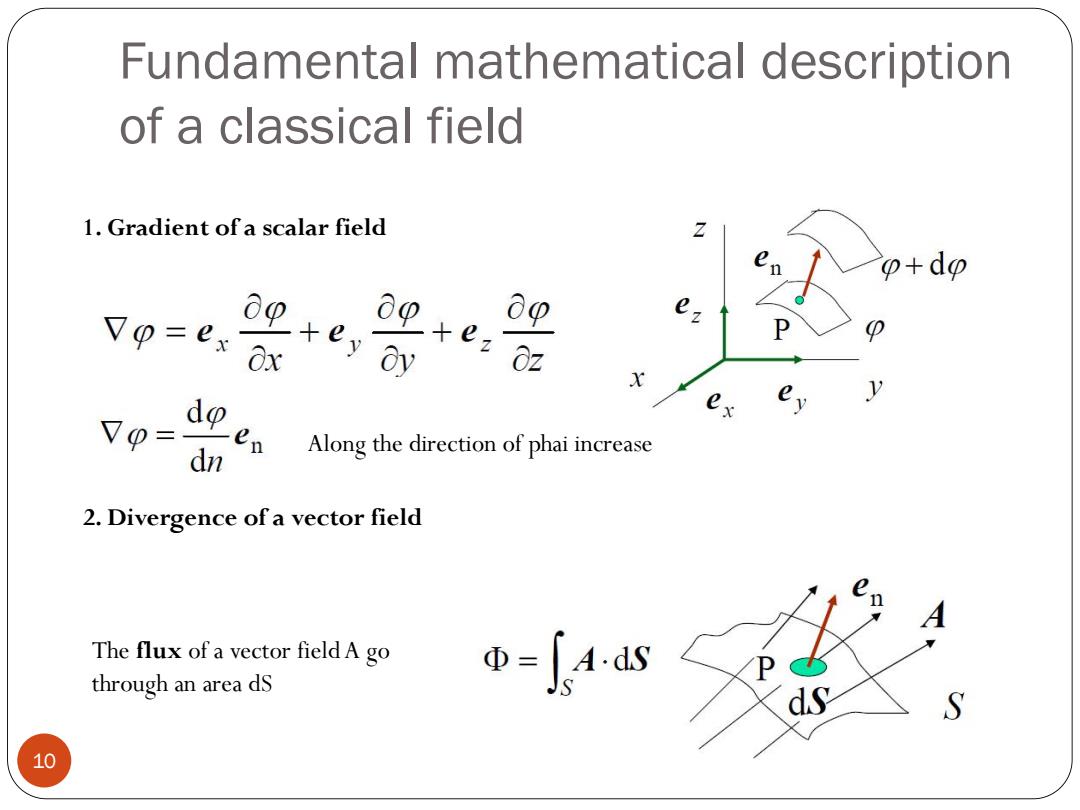
Fundamental mathematical description of a classical field 1.Gradient of a scalar field P+do o⑨+eyy o=ex Ox 09+ez02 00 1 V0二 dn Along the direction of phai increase 2.Divergence of a vector field The flux of a vector field A go through an area dS w-Jas 10
Fundamental mathematical description of a classical field 10 1. Gradient of a scalar field Along the direction of phai increase 2. Divergence of a vector field The flux of a vector fieldA go through an area dS