
同 第2章电路的分析方法 2.1电阻的串联和并联 2.2电压源与电流源及其等效变换 2.3支路电流法 2.4节点电压法 2.5叠加原理 2.6等效电源定理 2011-11-1
2011-11-1 1 第2章 电路的分析方法 2.1 电阻的串联和并联 2.2 电压源与电流源及其等效变换 2.3 支路电流法 2.4 节点电压法 2.5 叠加原理 2.6 等效电源定理 目录

同 第2章电路的分析方法 0⊙⊙0⊙@0◇@0⊙0◇⊙0⊙0◇⊙◇◇◇◇⊙◇◇◇◇⊙◇⊙⊙⊙◇⊙⊙0⊙⊙⊙⊙⊙ 本章要求: 1。熟练掌握节点电压法、叠加原理和戴维南定理 等电路的基本分析方法; 2.熟练掌握等效电阻的计算; 3.掌握实际电源的两种模型及其等效变换; 4.掌握用支路电流法、诺顿定理分析电路。 2011-11-1 2
2011-11-1 2 本章要求: 1. 熟练掌握节点电压法、叠加原理和戴维南定理 等电路的基本分析方法; 2. 熟练掌握等效电阻的计算; 3.掌握实际电源的两种模型及其等效变换; 4. 掌握用支路电流法、诺顿定理分析电路。 第2章 电路的分析方法 电路的分析方法
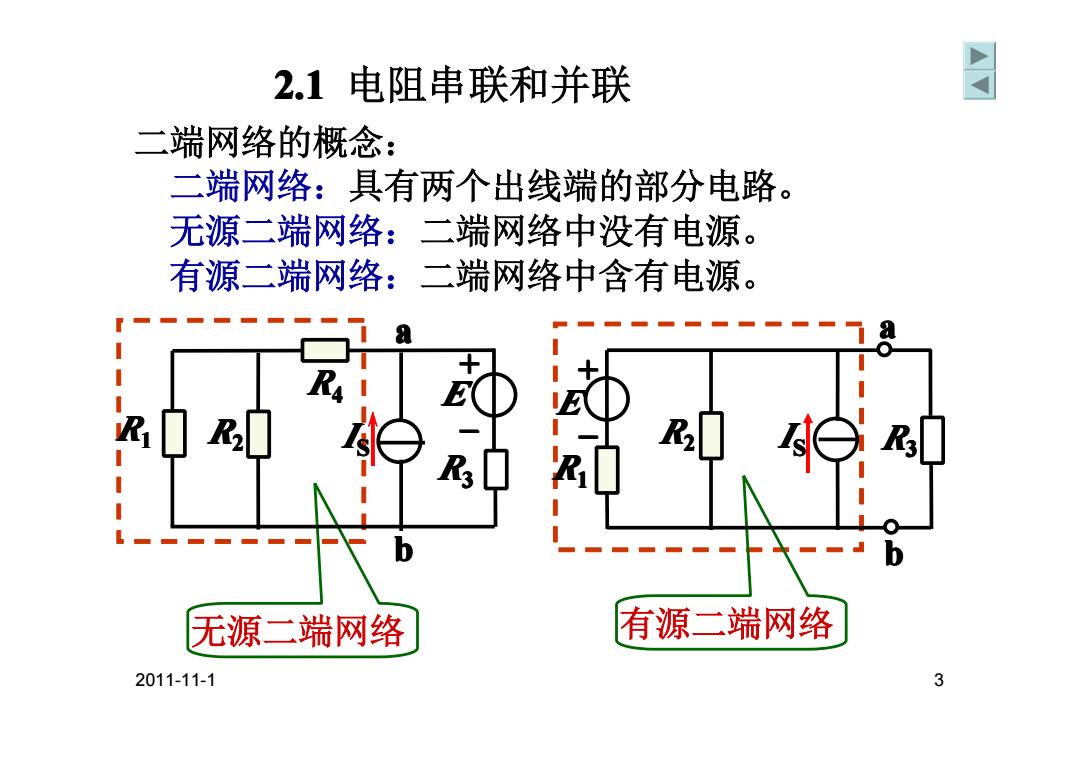
2.1电阻串联和并联 同 二端网络的概念: 二端网络:具有两个出线端的部分电路。 无源二端网络:二端网络中没有电源。 有源二端网络:二端网络中含有电源。 R E 2 3 无源二端网络 有源二端网络 2011-11-1 3
2011-11-1 3 二端网络的概念: 二端网络:具有两个出线端的部分电路。 无源二端网络:二端网络中没有电源。 有源二端网络:二端网络中含有电源。 无源二端网络 有源二端网络 b a E + R1 R – 2 I S R3 R4 b a E + – R1 R2 I S R3 2.1 电阻串联和并联
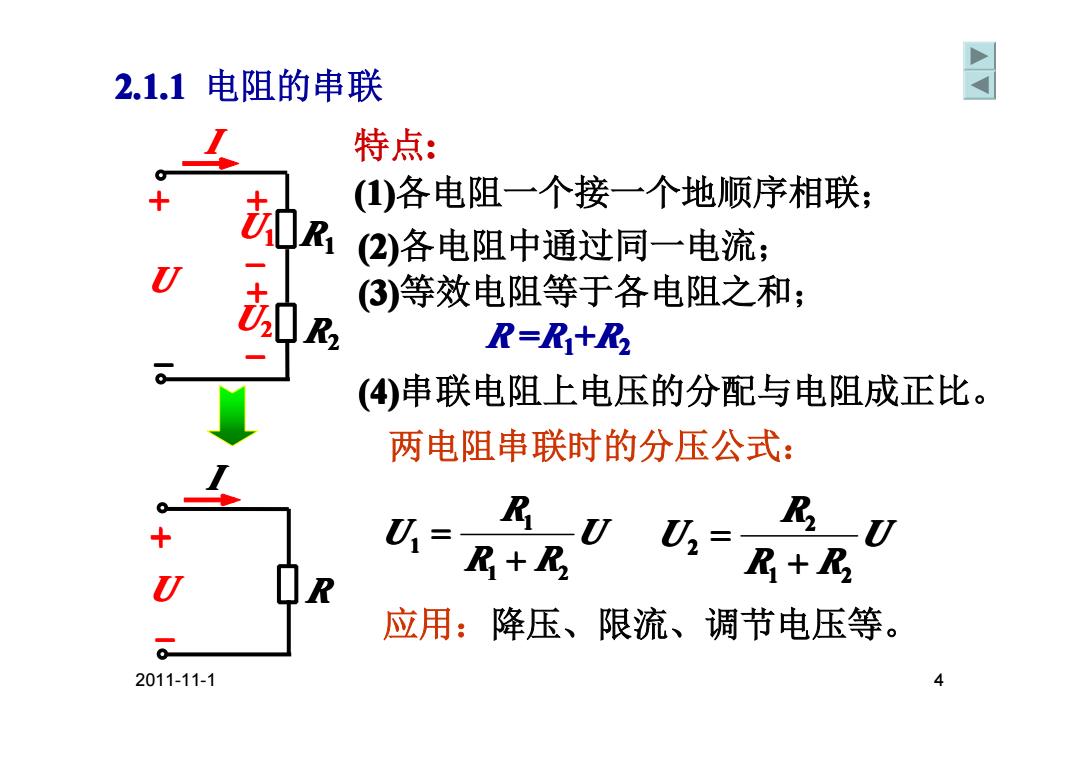
2.1.1电阻的串联 同 特点: (1)各电阻一个接一个地顺序相联; (2)各电阻中通过同一电流; U (③)等效电阻等于各电阻之和; 020 R R=R+R (4④)串联电阻上电压的分配与电阻成正比。 两电阻串联时的分压公式: R U=R+R R n U R+R 应用:降压、限流、调节电压等。 2011-11-1 4
2011-11-1 4 2.1.1 电阻的串联 特点: (1)各电阻一个接一个地顺序相联; 两电阻串联时的分压公式: U R R R U 1 2 1 1 + = U R R R U 1 2 2 2 + = R =R1+R2 (3)等效电阻等于各电阻之和; (4)串联电阻上电压的分配与电阻成正比。 R1 U1 U R2 U2 I + – + + – – U R I + – (2)各电阻中通过同一电流; 应用:降压、限流、调节电压等
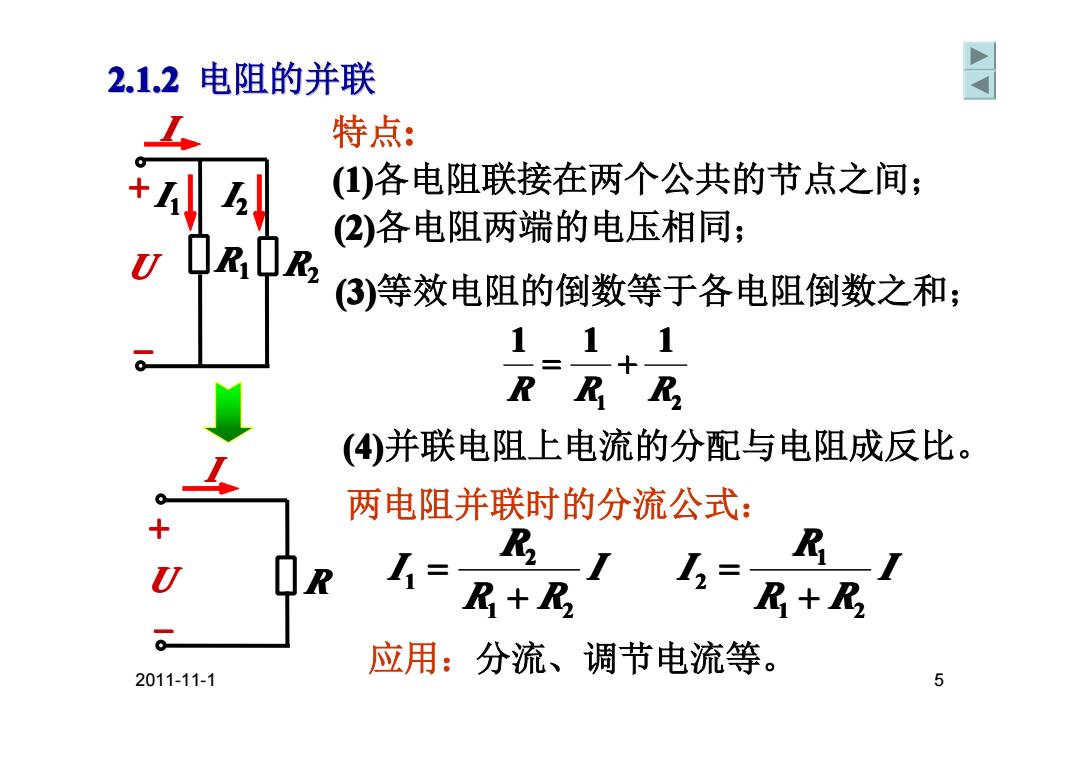
2.1.2电阻的并联 同 特点: (1)各电阻联接在两个公共的节点之间; (2)各电阻两端的电压相同; ③)等效电阻的倒数等于各电阻倒数之和; 1=1+1 (④)并联电阻上电流的分配与电阻成反比。 两电阻并联时的分流公式: E R R 1= R+R 12= R+R 应用:分流、调节电流等。 2011-11-1 5
2011-11-1 5 2.1.2 电阻的并联 两电阻并联时的分流公式: I R R R I 1 2 2 1 + = I R R R I 1 2 1 2 + = 1 2 1 1 1 R R R = + (3)等效电阻的倒数等于各电阻倒数之和; (4)并联电阻上电流的分配与电阻成反比。 特点: (1)各电阻联接在两个公共的节点之间; U R I + – I 1 I 2 U R1 R2 I + – (2)各电阻两端的电压相同; 应用:分流、调节电流等
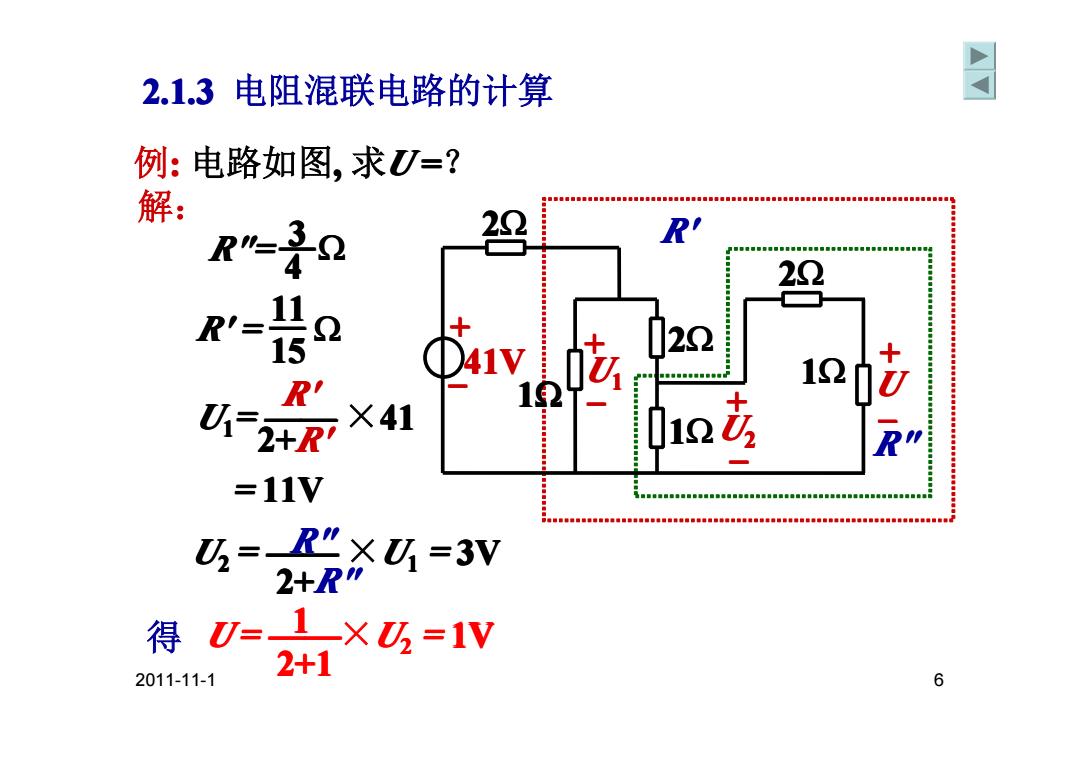
2.1.3电阻混联电路的计算 周 例:电路如图,求)=? 解: R=2 R 22 11 R'= 4y 十 15 022 R 12 12 U2+R' ×41 01n =11V 5=R"×=3V 2+R" 得0=1×=1V 2+1 2011-11-1 6
2011-11-1 6 R' R" 例: 电路如图, 求U =? 解: 2.1.3 电阻混联电路的计算 R"= R"= R"= R"= —Ω 4 3 U1= —— ×41 = 11V R' 2+R' U2 = ——R" ×U1 = 3V 2+R" U = ——×U2 = 1V 2+1 得 1 R' = R' = R' = R' = — Ω 15 11 + – 41V 2Ω 2Ω 2Ω 1Ω 1Ω 1Ω U2 U1 + – + – + –U
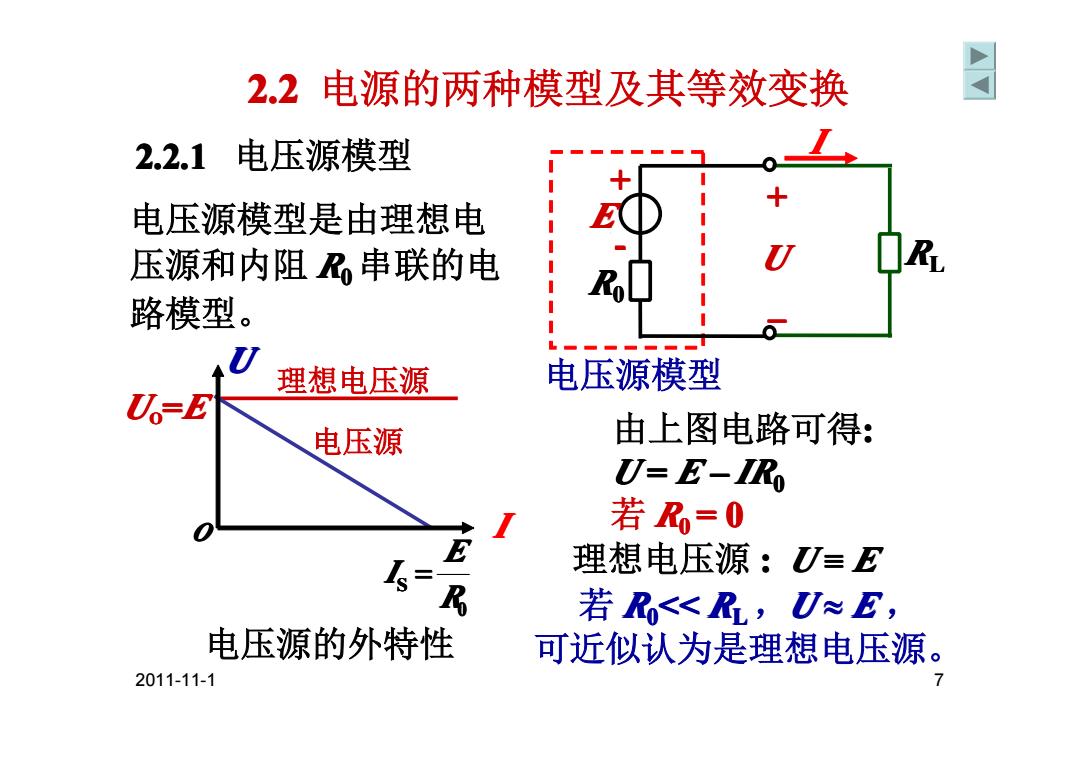
2.2电源的两种模型及其等效变换 国 2.2.1电压源模型 电压源模型是由理想电 压源和内阻串联的电 R 路模型。 理想电压源 电压源模型 Uo=E 电压源 由上图电路可得: U-E-IRo 若R=0 E 理想电压源:=E 乃 若R<R,U≈E, 电压源的外特性 可近似认为是理想电压源。 2011-11-1
2011-11-1 7 2.2 电源的两种模型及其等效变换 2.2.1 2.2.1 2.2.1 2.2.1 电压源模型 电压源模型 由上图电路可得: U = E – IR0 若 R0 = 0 理想电压源 : U ≡ E UO =E 电压源的外特性 I U I RL R0 + - E U + – 电压源模型是由理想电 压源和内阻 R0 串联的电 路模型。 0 S R E I = 若 R0<< RL ,U ≈ E , 可近似认为是理想电压源。 理想电压源 O 电压源
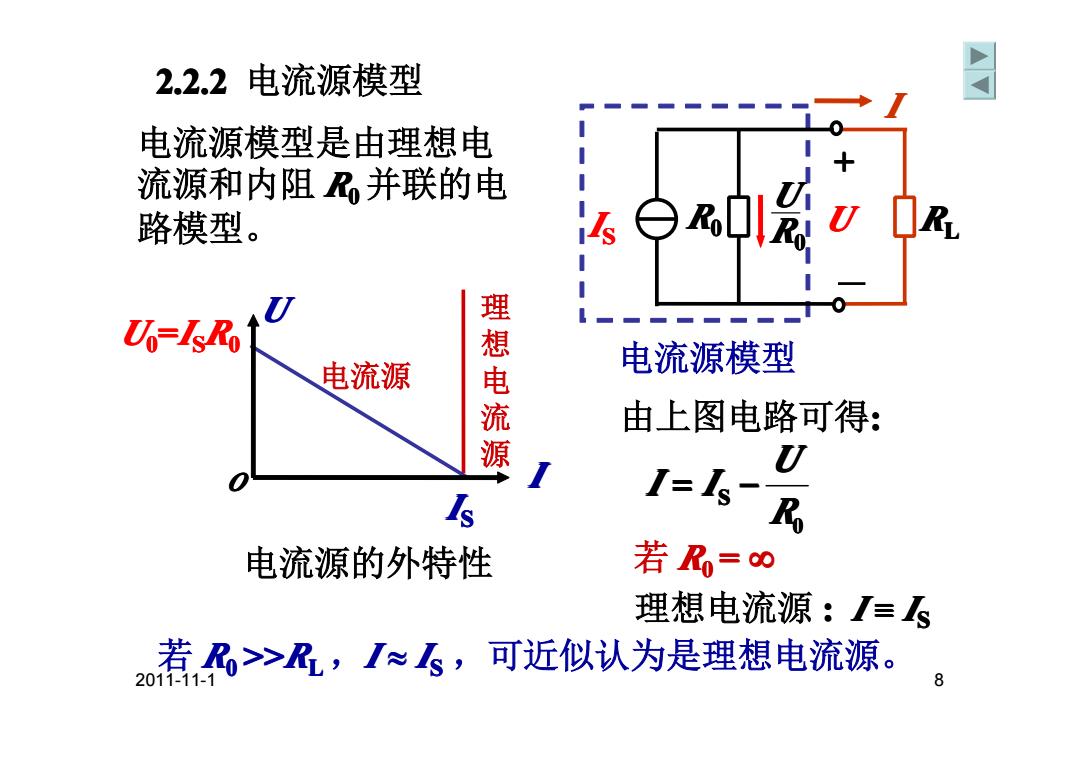
2.2.2电流源模型 电流源模型是由理想电 流源和内阻,并联的电 路模型。 R 理 Uo-ls Ro 想 电流源 电流源模型 流 由上图电路可得: U 公 电流源的外特性 若R=∞ 理想电流源:I≡S 若R>R,I≈飞,可近似认为是理想电流源。 2011-11- 8
2011-11-1 8 2.2.2 电流源模型 0 S R U I = I − I RL U0=I SR0 电流源的外特性 I U 理 想 电 流 源 O I S 电流源模型是由理想电 流源和内阻 R0 并联的电 路模型。 由上图电路可得: 若 R0 = ∞ 理想电流源 : I ≡ I S 若 R0 >>RL ,I ≈ I S ,可近似认为是理想电流源。 电流源 电流源模型 R0 R U 0 U I S +-
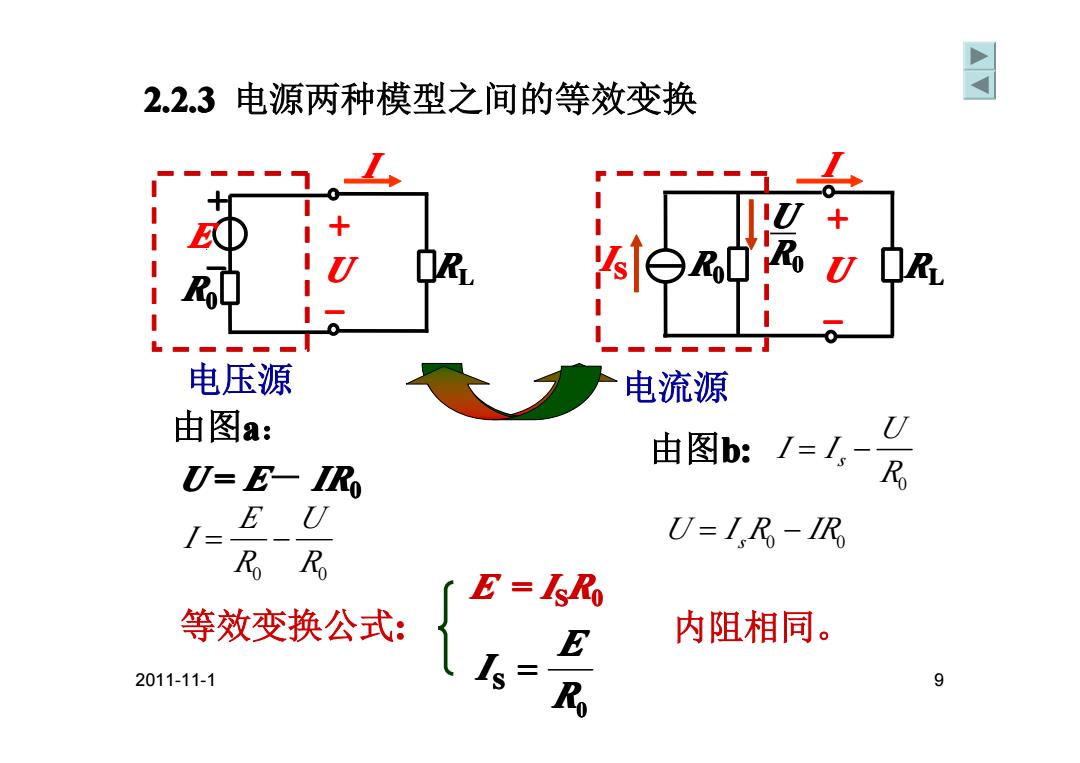
2.2.3电源两种模型之间的等效变换 周 电压源 电流源 由图a: 由图b:1=1,- U-E IRo R E U U=I R-IRo Ro Ro E =Isko 等效变换公式: E 内阻相同。 2011-11-1 9
2011-11-1 9 2.2.3 电源两种模型之间的等效变换 由图a: U = E- IR0 I RL R0 + –E U + – 电压源 等效变换公式: E = I SR0 0 S R E I = R0 U RL R0 U I S I + – 电流源 0 R0 U R E I = − 由图b: 0 s U I I R = − U I R IR = − s 0 0 内阻相同
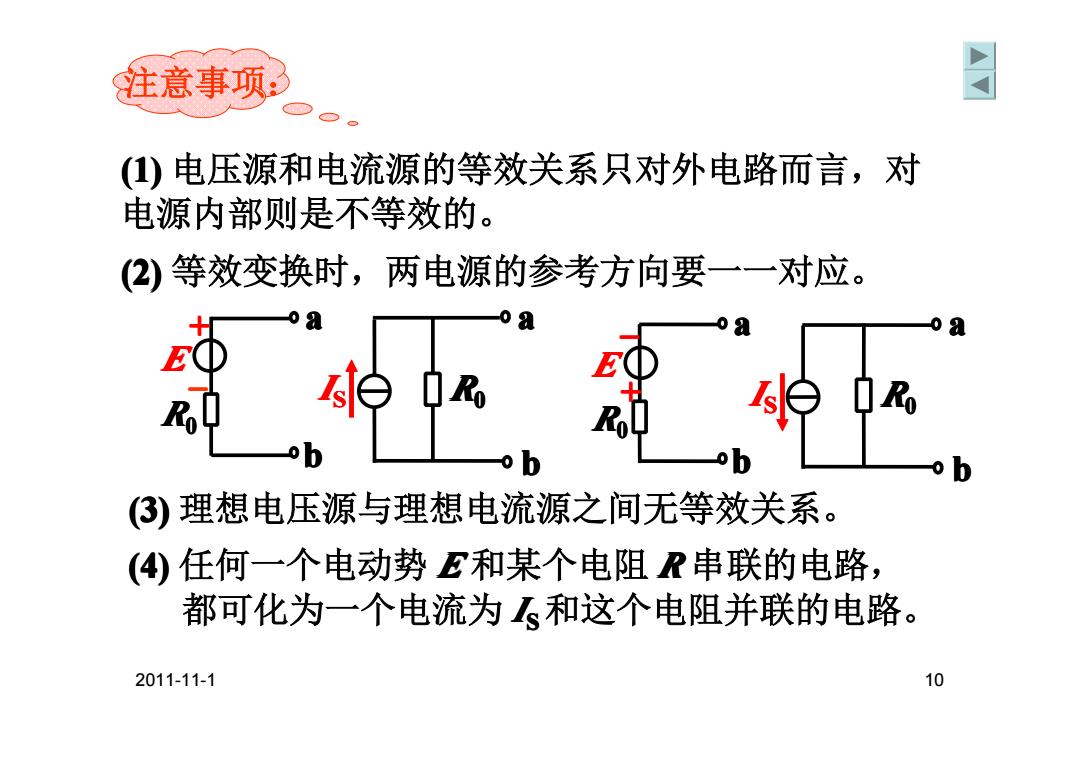
注意事项: 同 (1)电压源和电流源的等效关系只对外电路而言,对 电源内部则是不等效的。 (2)等效变换时,两电源的参考方向要一一对应。 o a Ko b ③)理想电压源与理想电流源之间无等效关系。 (④任何一个电动势E和某个电阻R串联的电路, 都可化为一个电流为和这个电阻并联的电路。 2011-11-1 10
2011-11-1 10 (2) 等效变换时,两电源的参考方向要一一对应。 (3) 理想电压源与理想电流源之间无等效关系。 (1) 电压源和电流源的等效关系只对外电路而言,对 电源内部则是不等效的。 注意事项: (4) 任何一个电动势 E 和某个电阻 R 串联的电路, 都可化为一个电流为 I S 和这个电阻并联的电路。 R0 + – E a b I S R0 a b R0–+ E a b I S R0 a b