山东理工大学：《电路》课程教学资源（课件讲稿）第4章 电路定理

第四章： 电路定理 内容提要 1.叠加定理 难点：各电路 齐性定理 定理应用的条 2.替代定理 件、电路定理 3.戴维南定理和诺顿定理 应用中受控源 4.特勒根定理 的处理。 5.互易定理 6.对偶原理 2010年3月3日星期三

2010年3月3日星期三 1 第四章 电路定理 内容提要 1. 叠加定理 齐性定理 2. 替代定理 3. 戴维南定理和诺顿定理 4. 特勒根定理 5. 互易定理 6. 对偶原理 难点：各电路 定理应用的条 件、电路定理 应用中受控源 的处理

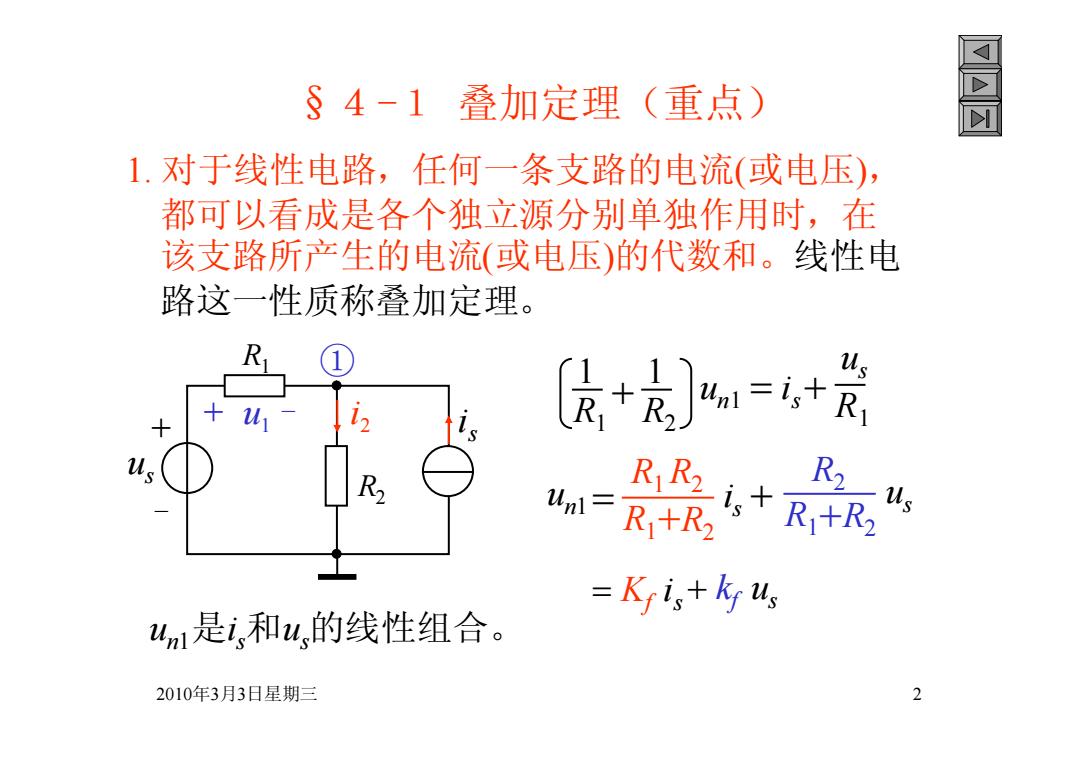
§4-1叠加定理（重点） 1.对于线性电路，任何一条支路的电流（或电压）， 都可以看成是各个独立源分别单独作用时，在 该支路所产生的电流（或电压）的代数和。线性电 路这一性质称叠加定理。 R us [员+元]4=+ D R R2 R um=R+R2 s+Ri+R2 =Kristh us 4n1是i,和u,的线性组合。 2010年3月3日星期三 2

2010年3月3日星期三 2 §４-１ 叠加定理（重点） 1. 对于线性电路，任何一条支路的电流(或电压)， 都可以看成是各个独立源分别单独作用时，在 该支路所产生的电流(或电压)的代数和。线性电 路这一性质称叠加定理。 + - us R1 i s R2 i + 2 u - 1 ① R1 1 R2 1 un1 i sR1 us un1 R1+R2 R1R2 i s R1+R2 R2 us Kf i s kf us un1是i s和us的线性组合

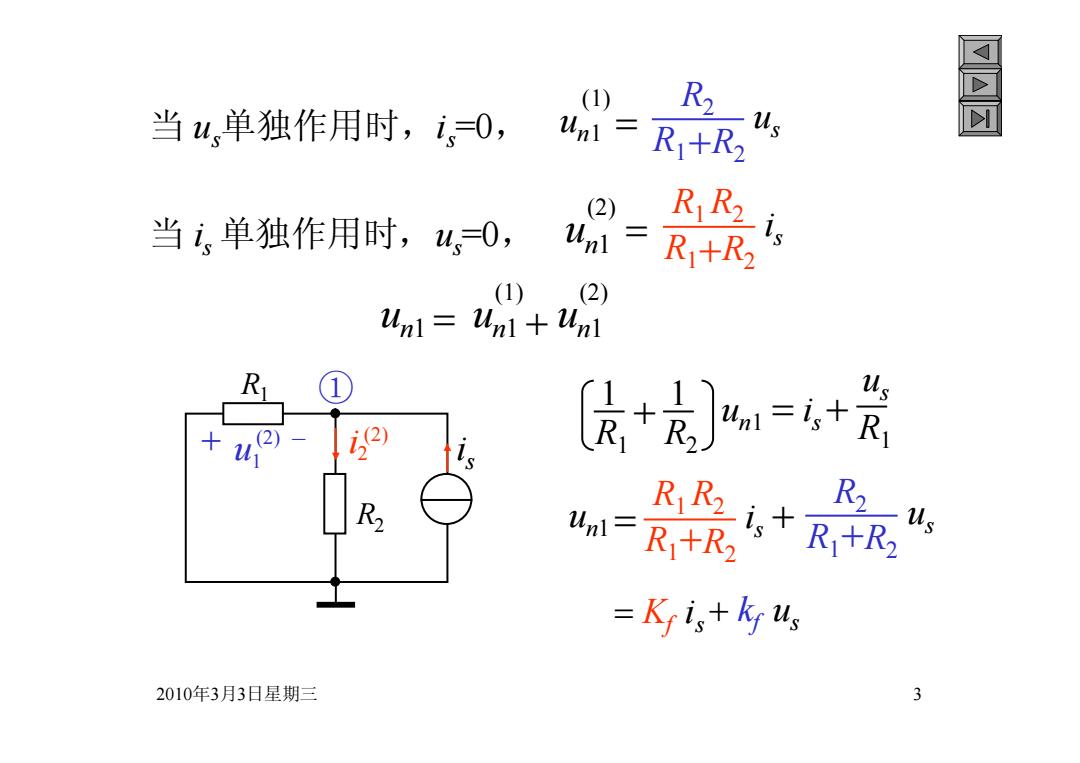
(1) R2 当u单独作用时，i,=0,unl= 哥 R1+R2 当i、单独作用时，u,=0, 兴经 (2) Unl (1) ) Unl Unl Unl R [民+]=+ s 十 (2) RiR>is+RyR2 Um=R+R2 =K isthy us 2010年3月3日星期三 3

2010年3月3日星期三 3 + - us R1 i s R2 i + 2 u - 1 ① 当 us单独作用时，i s=0， 当 i s 单独作用时，us=0， un1 (1)  un1 (2) R1R2 R2 us R1R2 R1R2 i s un1 un1 (1) un1 (2) ① + - R1 R2 i + 2 - u1 (1) (1) us R1 i s R2 i + 2 - u1 (2) (2) ① R1 1 R2 1 un1 i sR1 us un1 R1+R2 R1R2 i s R1+R2 R2 us Kf i s kf us

对于任何线性电路，当电路有g个电压源和h个 E 电流源时，任意一处的电压和电流都可以写 成以下形式： 5三4+上K h m= -2的4+空K h m= M= ·叠加原理是线性电路的根本属性，它一方面可以 用来简化电路计算，另一方面，线性电路的许多 定理可以从叠加定理导出。在线性电路分析中， 叠加原理起重要作用。 2010年3月3日星期三 4

2010年3月3日星期三 4 • 叠加原理是线性电路的根本属性，它一方面可以 用来简化电路计算，另一方面，线性电路的许多 定理可以从叠加定理导出。在线性电路分析中， 叠加原理起重要作用。 对于任何线性电路，当电路有g个电压源和h个 电流源时，任意一处的电压uf和电流i f都可以写 成以下形式： uf ∑ m=1 g kf m us Kf m i +∑ s m=1 h i f ∑ m=1 g k'f m us K'f m i +∑ s m=1 h

2.应用叠加定理时注意以下各点： E (1)叠加定瀆不Ⅻ用于非线性电路： (2)叠加时，电路的联接以及电路所有电阻和受控 源都不予更动。 所谓电压源不作用，是戊该电压源的电压置 零，即在该电压源处用短路替代： 电流源不作用，是把该电流源的电流置，即 在该电流处用开路替代； (3)叠加时要汨意电流同电压的参考方向； (4)功率不能叠加！ (5)电源分别作用时，可以“单干”，也可以按组。 2010年3月3日星期三

2010年3月3日星期三 5 2. 应用叠加定理时注意以下各点： (1)叠加定瀆不ဂ 用于非线性电路； (2)叠加时，电路的联接以及电路所有电阻和受控 源都不予更动。 所谓电压源不作用，是戊该电压源的电压置 零，即在该电压源处用短路替代； 电流源不作用，是把该电流源的电流置 ，即 在该电流处用开路替代； (3)叠加时要汨意电流同电压的参考方向； (4)功率不能叠加！ (5)电源分别作用时，可以“单干” ，也可以按组

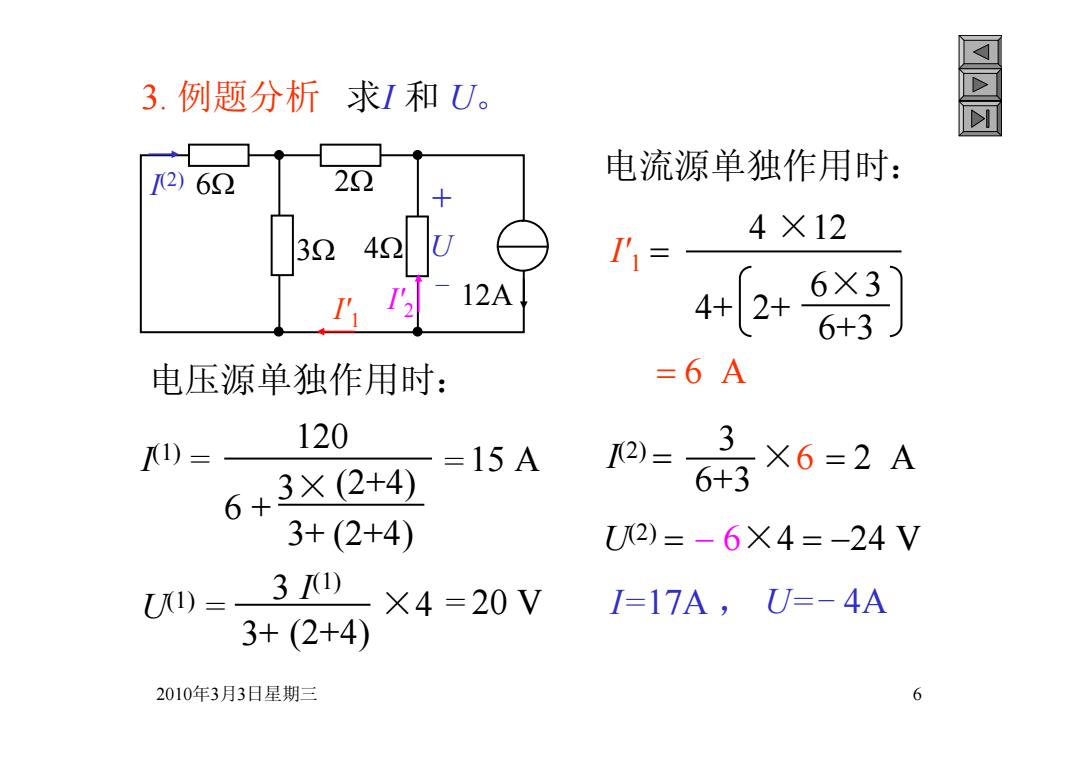
3.例题分析求I和U。 电流源单独作用时： 2)62 4×12 32 '= 12A 4[2 6×3 电压源单独作用时： =6A 120 1)= 6+3×(2+4) =15A 2)= 3 X6=2A 6+3 3+(2+4) U2)=-6×4=-24V U1)= 311) ×4=20V I=17A,U=-4A 3+(2+4) 2010年3月3日星期三 6

2010年3月3日星期三 6 3. 例题分析 求I 和 U。 电压源单独作用时： 电流源单独作用时： + - 120V I U - 6 3 4 2 12A + I (1) = 3+ (2+4) 3×(2+4) 6 + 120 =15 A U(1) = 3+ (2+4) 3 I (1) ×4 =20 V I'1  6×3 6+3 4+ 2+ 4 ×12 6 A I (2)  3 6+3 ×6 2 A U(2) 6×4 24 V I=17A ， U=- 4A (1) I (2) U - 6 3 4 2 12A + I'1 I'2

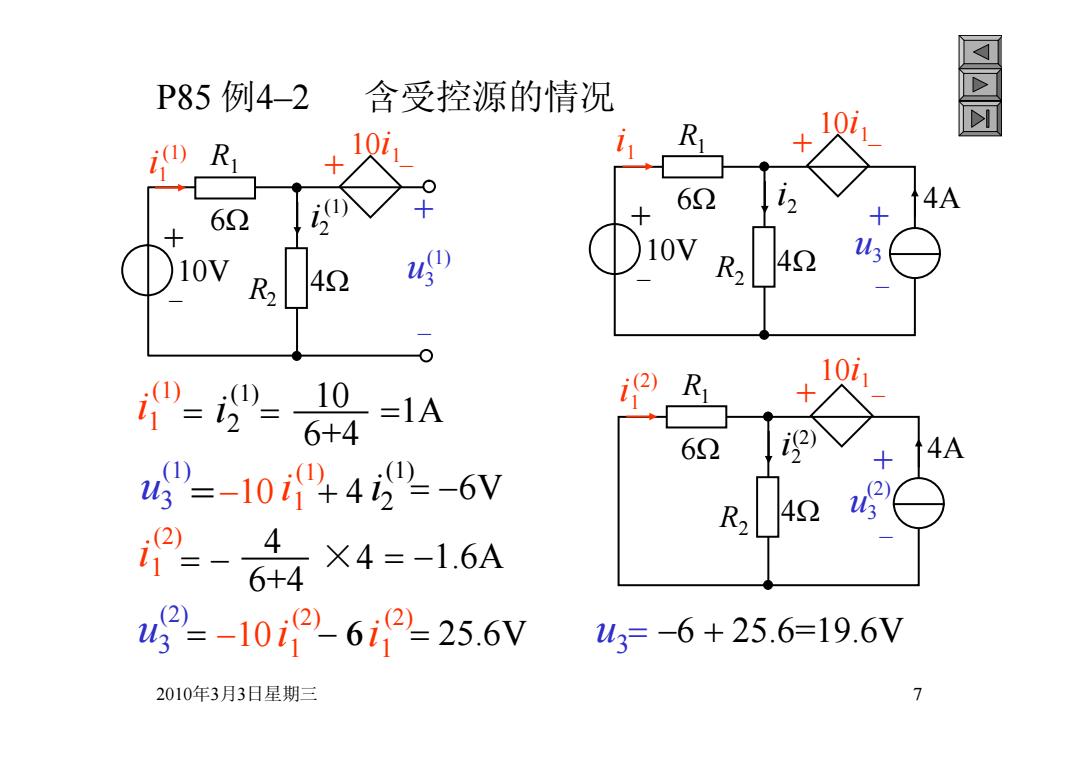
P85例4-2 含受控源的情况 R 10i R 6 4A 6Ω 10 42 10i1 "==0=1A 6+4 62 4A 4g-104-6V - (2) ×4=-1.6A 6+4 4g2=-102612=25.6V u3=-6+25.6=19.6V 2010年3月3日星期三 7

2010年3月3日星期三 7 P85 例4–2 含受控源的情况 u36 25.6=19.6V 10i 1 + - 10V R1 4A R2 i 2 + - u3 6 i 1 4 + - i 1 (1) i 2 (1)  6+4 10 1A u3 (1) =10 i 1 (1)4 i 2 (1) 6V i 1 (2) 6+4 4 ×4 1.6A u3 (2) 10 i 1 (2)i 1 (2) 25.6V 10i 1 + - 10V R1 R2 i 2 + - u3 6 i 1 4 + - (1) (1) (1) 10i R 1 1 4A R2 i 2 + - u3 6 i 1 4 + - (2) (2) (2)

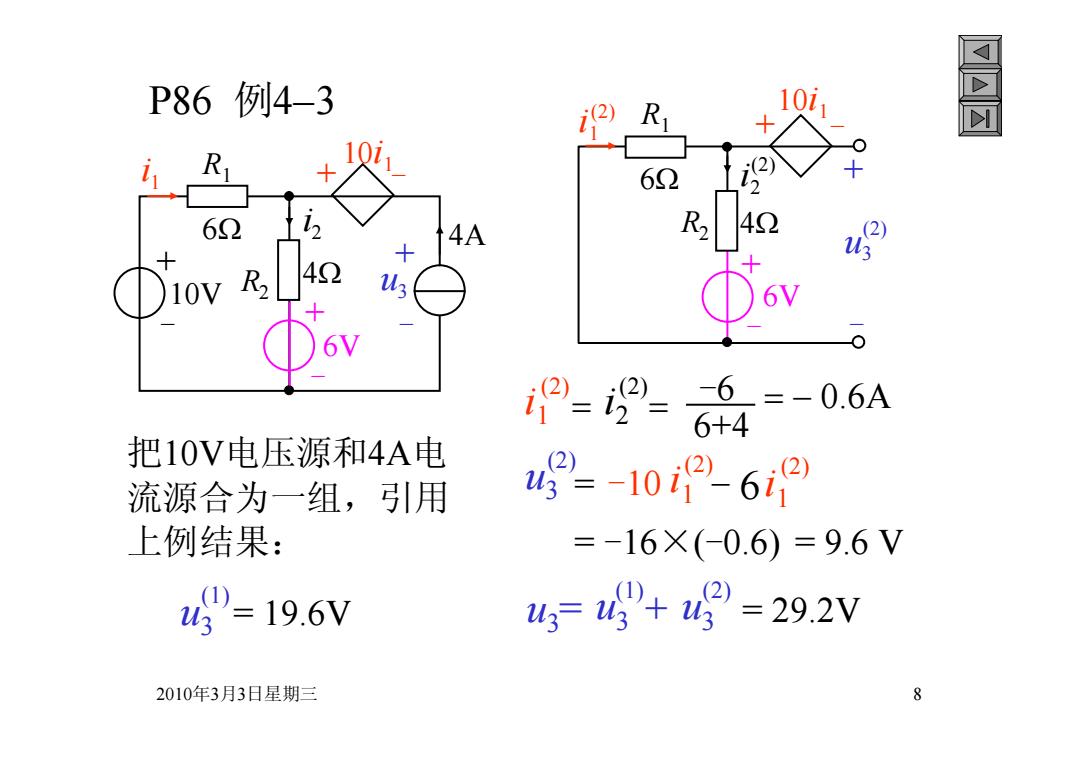
P86例4-3 R 101 哥 R 62 6 4A (2) 6V ===-0.6A 6+4 把10V电压源和4A电 流源合为一组，引用 4g2=-109-62 上例结果： =-16×(-0.6)=9.6V u=19.6V 4=4+42=29.2V 2010年3月3日星期三 8

2010年3月3日星期三 8 P86 例4–3 10i 1 + - 10V R1 4A R2 i 2 + - u3 6 i 1 4 + - + - 6V u3 = 19.6V (1) 把10V电压源和4A电 流源合为一组，引用 上例结果： i 1 (2) i 2 (2)  6+4 -6 0.6A u3 (2) = -10 i 1 (2) - 6i 1 (2) = -16×(-0.6) 10i 1 + - 6V R1 R2 i 2 + - u3 6 i 1 4 + - (2) (2) (2) = 9.6 V u3 = u3 = 29.2V (1)+ u3 (2)

K%-[24三K可K 4.齐性定理 fKx)=K.fx) ·当所有激励（电压源和电流源）都增大或缩小K倍 (K为实常数)时，响应（电流和电压）也将同样增 大或缩小K倍。 ·首先，激励指独立电源； ·其次，必须全部激励同时增大或缩小K倍。 显然，当电路中只有一个激励时，响应将与激 励成正比。 ·用齐性定理分析梯形电路特别有效。 2010年3月3日星期三 9

2010年3月3日星期三 9 4. 齐性定理 f(Kx) = K f(x) • 当所有激励(电压源和电流源)都增大或缩小K倍 (K为实常数)时，响应(电流和电压)也将同样增 大或缩小K倍。 • 首先，激励指独立电源； • 其次，必须全部激励同时增大或缩小K倍。 • 显然，当电路中只有一个激励时，响应将与激 励成正比。 • 用齐性定理分析梯形电路特别有效。 uf = ∑ m=1 g kf m us Kf m i +∑ s m=1 h K K

P87例4-4 Ais R3 B is Rs 哥 求各支路电流。 22 i222↓i422 先用“倒退法” 120V R R6 202 设i5=i'5=1A S 202- 202 C u'Bc=(2+20)i'5=22V u'ac 26.2 =1.31A 4= W8c= 22=1.1A R2 20 20 i1=2+i'3=3.41A 3=4+5=2.1A u's Ri'+u'ac u'ac R3i'3+u'Bc =2×3.41+26.2 =2×2.1+22=26.2V =33.02V 2010年3月3日星期三 10

2010年3月3日星期三 10 P87 例4–4 求各支路电流。 先用“倒退法” 设 i5i'5 1A + - 120V R1 R2 i 2 2 i 1 u 20 S R3 2 i 3 i 4 R4 20 R5 2 i 5 R6 20 A B C u'BC (220) i'522V i'4  u'BC R4  22 20 1.1A i'3i'4i'5 2.1A u'AC R3 i'3u'BC 2×2.122 26.2V i'2  u'AC R2  26.2 20 1.31A i'1 i'2i'3 3.41A u'S R1 i'1u'AC = 2×3.41+26.2 =33.02V