
第十六章二端口网络 内容提要 1.二端口的概念、方程及参数; 2.各参数方程形式,参数的含义及求法; 3.二端口转移函数及求法; 4.特性阻抗的定义及求法; 5.二端口等效电路的概念,等效电路的结构 及参数; 6.二端口级联、串联、并联的条件与等效参 数的求法: 7.回转器、负阻变换器的定义与特性。 2010年3月3日星期三 1
2010年3月3日星期三 1 结束 第十六章 二端口网络 内容提要 1. 二端口的概念、方程及参数; 2. 各参数方程形式,参数的含义及求法; 3. 二端口转移函数及求法; 4. 特性阻抗的定义及求法; 5. 二端口等效电路的概念,等效电路的结构 及参数; 6. 二端口级联、串联、并联的条件与等效参 数的求法; 7. 回转器、负阻变换器的定义与特性

基本要求 1.掌握与每种参数相对应的二端口网络方程,理 解这些方程各自参数的物理意义; 2.掌握二端口等效电路; 3.掌握二端口在不同连接方式时的分析方法: 4.掌握分析特殊二端口的方法。 重点和难点 重点:两端口的方程和参数的求解。 Y难点:二端口的参数的求解。 2010年3月3日星期三 2
2010年3月3日星期三 2 基本要求 结束 1. 掌握与每种参数相对应的二端口网络方程,理 解这些方程各自参数的物理意义; 2. 掌握二端口等效电路; 3. 掌握二端口在不同连接方式时的分析方法; 4. 掌握分析特殊二端口的方法。 重点和难点 重点:两端口的方程和参数的求解。 难点:二端口的参数的求解
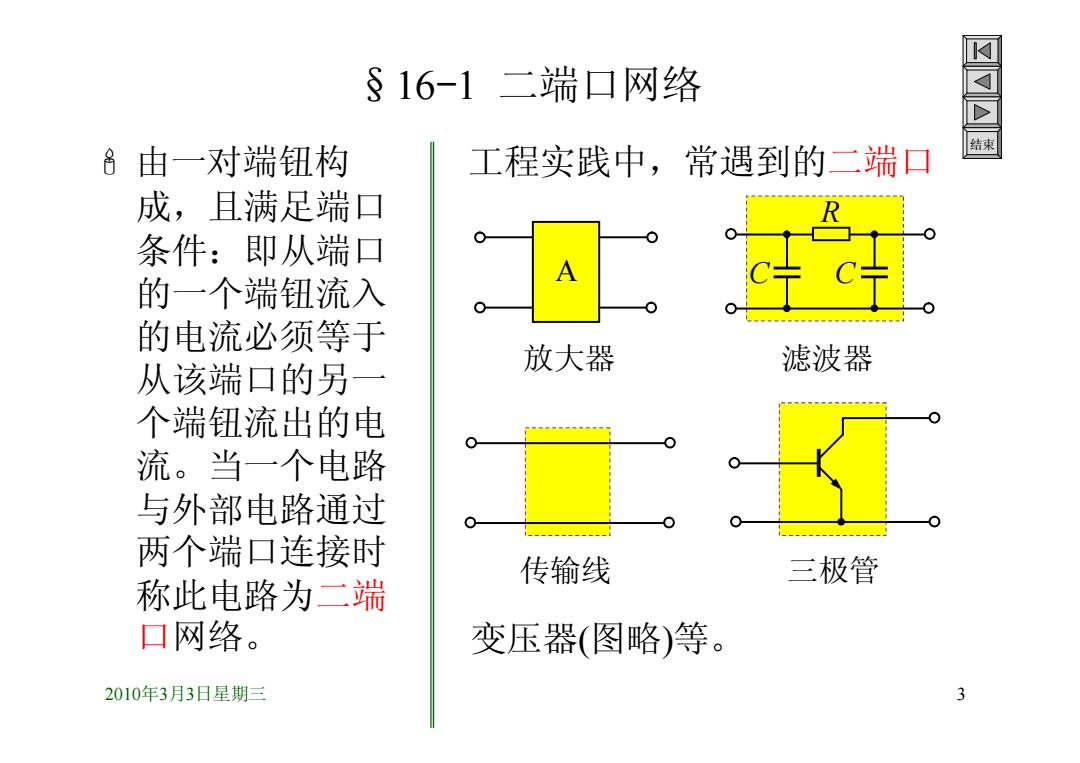
§16-1二端口网络 结束 由一对端钮构 工程实践中,常遇到的二端口 成,且满足端口 条件:即从端口 A 的一个端钮流入 的电流必须等于 从该端口的另一 放大器 滤波器 个端钮流出的电 流。当一个电路 与外部电路通过 两个端口连接时 传输线 三极管 称此电路为二端 口网络。 变压器(图略)等。 2010年3月3日星期三 3
2010年3月3日星期三 3 结束 §16-1 二端口网络 由一对端钮构 成,且满足端口 条件:即从端口 的一个端钮流入 的电流必须等于 从该端口的另一 个端钮流出的电 流。当一个电路 与外部电路通过 两个端口连接时 称此电路为二端 口网络。 工程实践中,常遇到的二端口 A 放大器 R C C 滤波器 传输线 三极管 变压器(图略)等
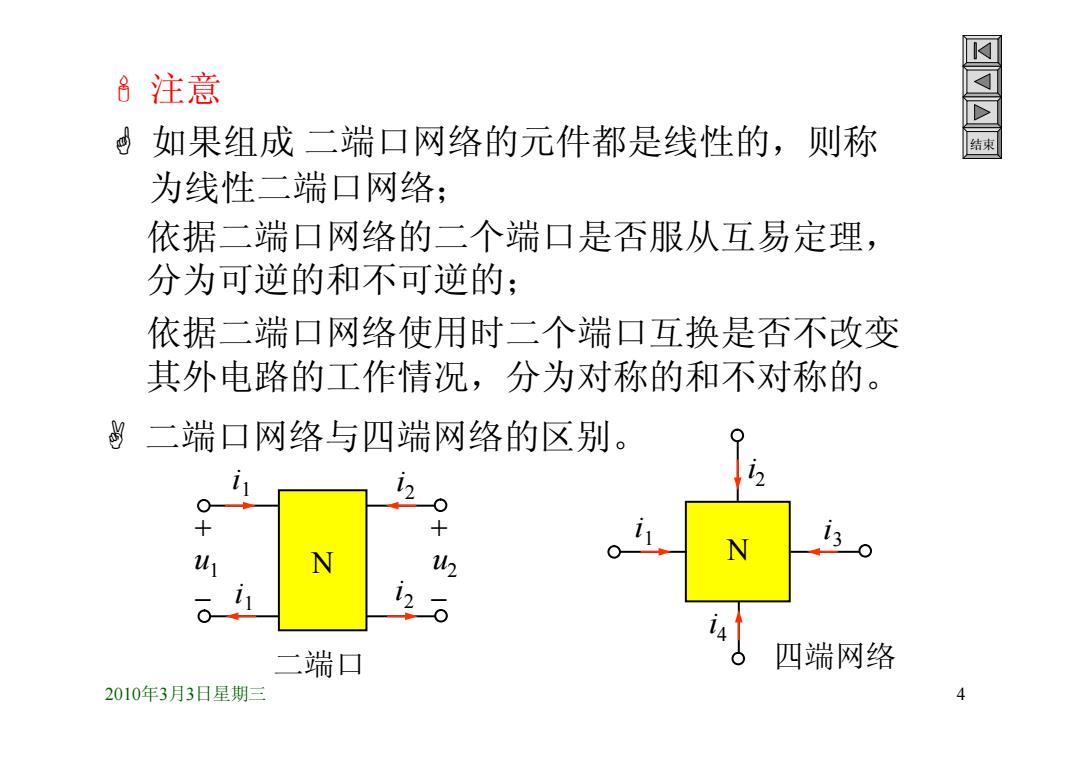
8注意 电如果组成二端口网络的元件都是线性的,则称 为线性二端口网络; 依据二端口网络的二个端口是否服从互易定理, 分为可逆的和不可逆的; 依据二端口网络使用时二个端口互换是否不改变 其外电路的工作情况,分为对称的和不对称的。 二端口网络与四端网络的区别。 + u N h N 二端口 四端网络 2010年3月3日星期三 4
2010年3月3日星期三 4 结束 注意 如果组成 二端口网络的元件都是线性的,则称 为线性二端口网络; 依据二端口网络的二个端口是否服从互易定理, 分为可逆的和不可逆的; 依据二端口网络使用时二个端口互换是否不改变 其外电路的工作情况,分为对称的和不对称的。 二端口网络与四端网络的区别。 u1 i 1 i 1 u2 i 2 i 2 N N i 1 i 2 i 3 i 4 二端口 四端网络
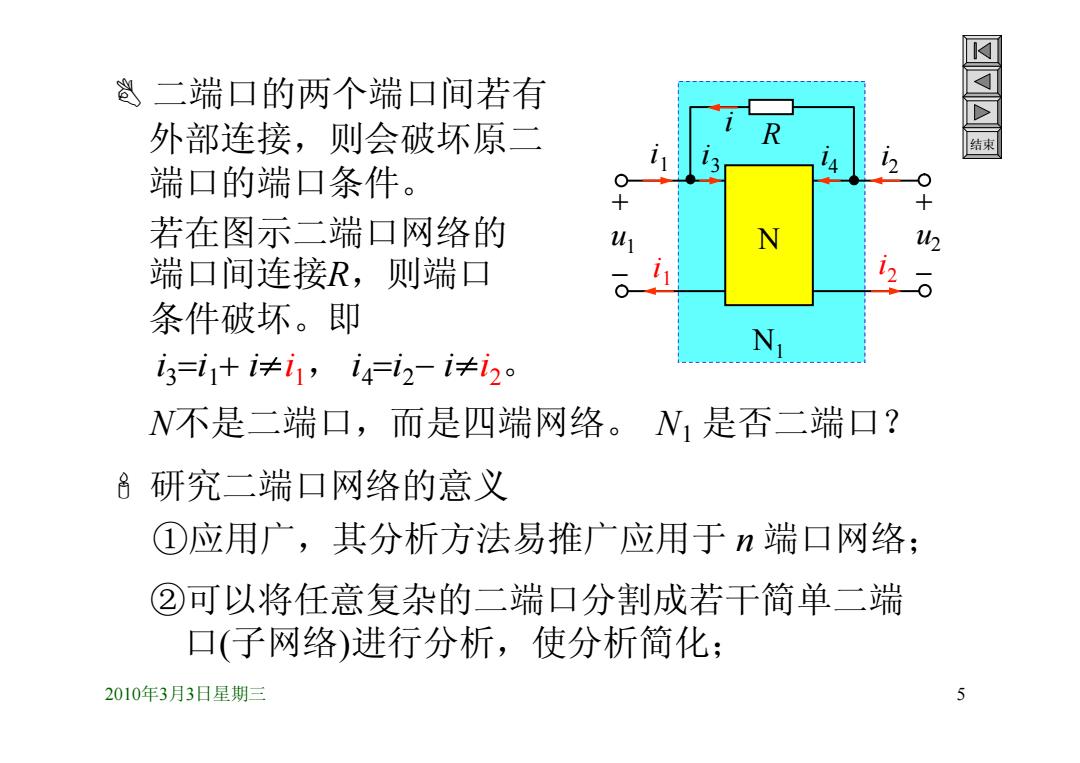
邕二端口的两个端口间若有 外部连接,则会破坏原二 端口的端口条件。 若在图示二端口网络的 u N 端口间连接R,则端口 条件破坏。即 N i3=i1+i≠i1,4i2-i≠i2。 N不是二端口,而是四端网络。N1是否二端口? 研究二端口网络的意义 ①应用广,其分析方法易推广应用于端口网络; ②可以将任意复杂的二端口分割成若干简单二端 口(子网络)进行分析,使分析简化; 2010年3月3日星期三 5
2010年3月3日星期三 5 结束 N1 二端口的两个端口间若有 外部连接,则会破坏原二 端口的端口条件。 若在图示二端口网络的 端口间连接R,则端口 条件破坏。即 u1 i 1 i 1 u2 i 2 i 2 N i R i 3 i 4 i3i1i≠i1, i4i2i≠i2。 N不是二端口,而是四端网络。 N1 是否二端口? 研究二端口网络的意义 ①应用广,其分析方法易推广应用于 n 端口网络; ②可以将任意复杂的二端口分割成若干简单二端 口(子网络)进行分析,使分析简化;
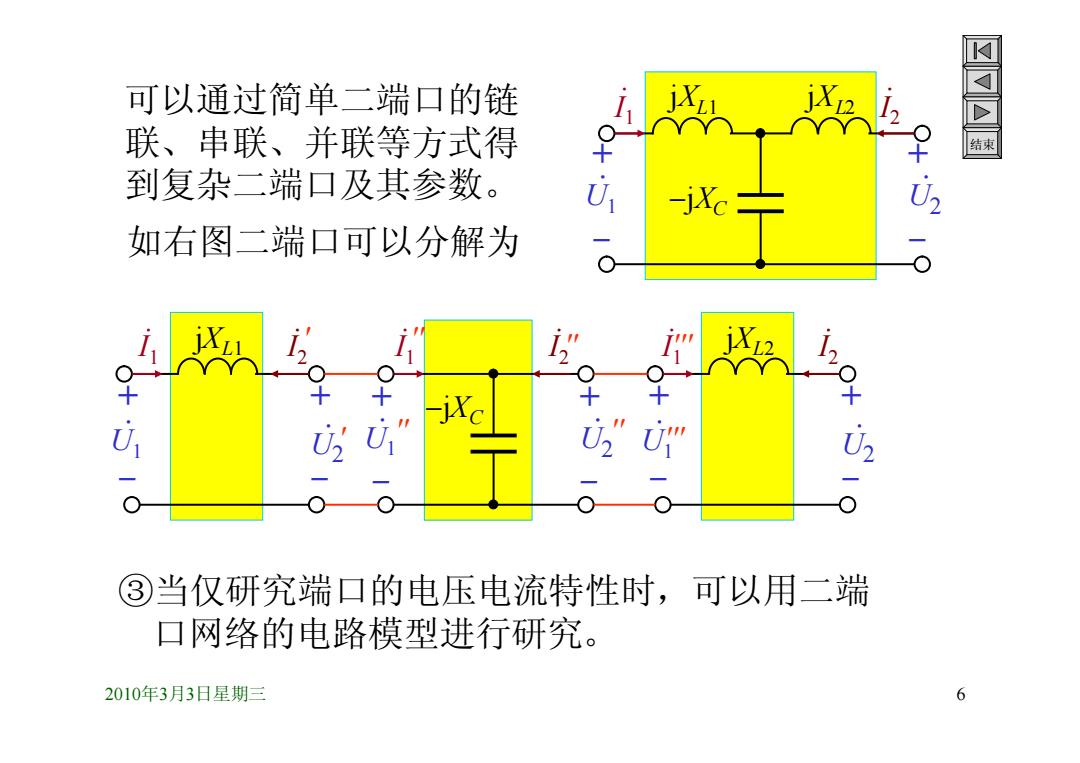
可以通过简单二端口的链 联、串联、并联等方式得 到复杂二端口及其参数。 U -jXc三 如右图二端口可以分解为 U U ③当仅研究端口的电压电流特性时,可以用二端 口网络的电路模型进行研究。 2010年3月3日星期三 6
2010年3月3日星期三 6 结束 + - . I 1 . U2 + - . U1 jXL1 . I 2 jXC jXL2 . I 1 + - . U1 jXL1 . I 2 + - . U2 ' ' + - . I 1 . U2 + - . U1 . I 2 jXC '' '' '' '' . I 1 + - . U1 jXL2 . I 2 + - . U2 ''' ''' 如右图二端口可以分解为 ③当仅研究端口的电压电流特性时,可以用二端 口网络的电路模型进行研究。 可以通过简单二端口的链 联、串联、并联等方式得 到复杂二端口及其参数
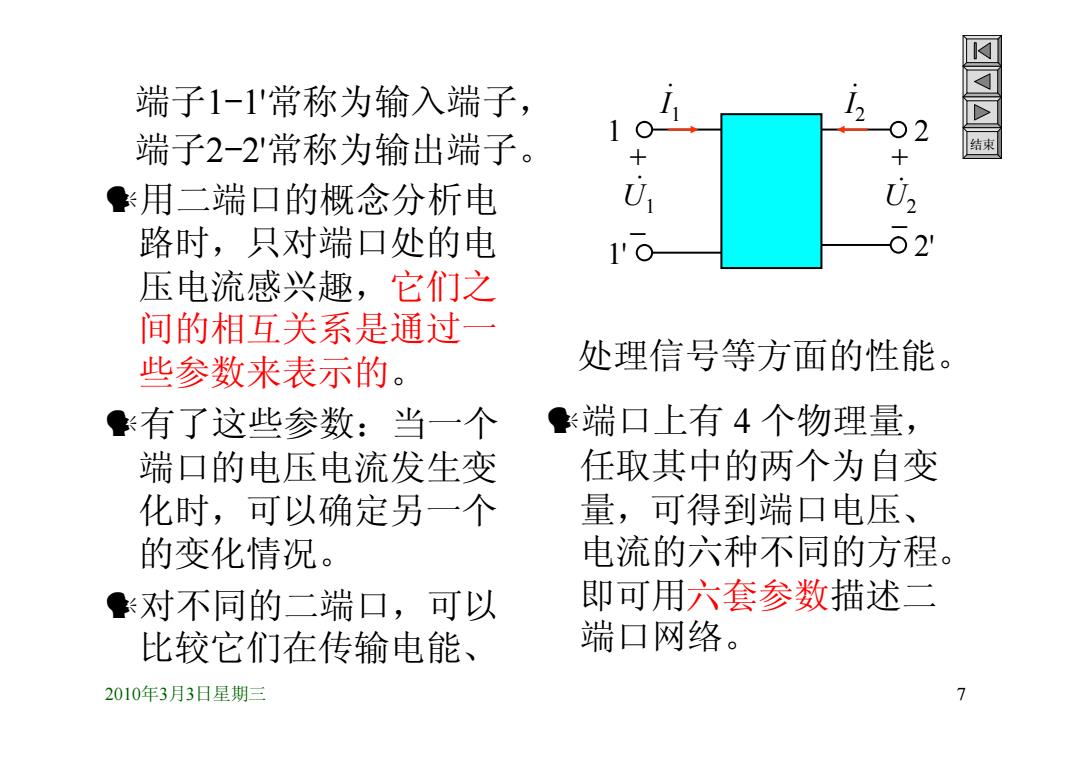
端子1-1'常称为输入端子, 端子2-2'常称为输出端子。 用二端口的概念分析电 U 02 路时,只对端口处的电 1'0 62} 压电流感兴趣,它们之 间的相互关系是通过一 些参数来表示的。 处理信号等方面的性能。 有了这些参数:当一个 ◆端口上有4个物理量, 端口的电压电流发生变 任取其中的两个为自变 化时,可以确定另一个 量,可得到端口电压 、 的变化情况。 电流的六种不同的方程。 对不同的二端口,可以 即可用六套参数描述二 比较它们在传输电能、 端口网络。 2010年3月3日星期三 7
2010年3月3日星期三 7 结束 端子1-1'常称为输入端子, 端子2-2'常称为输出端子。 用二端口的概念分析电 路时,只对端口处的电 压电流感兴趣,它们之 间的相互关系是通过一 些参数来表示的。 有了这些参数:当一个 端口的电压电流发生变 化时,可以确定另一个 的变化情况。 对不同的二端口,可以 比较它们在传输电能、 . I 1 . I 2 . U1 . U2 1 1' 2 2' 端口上有 4 个物理量, 任取其中的两个为自变 量,可得到端口电压、 电流的六种不同的方程。 即可用六套参数描述二 端口网络。 处理信号等方面的性能

§16-2二端口的方程和参数 一、Y(导纳)参数方程及Y参数 1.方程 由于是线性二端口, U 故用叠加原理可得 i,=Y11U+Y12U2 2.Y(导纳)参数 i2=Y21U1+Y22U def 写成矩阵形式: LY21Y2」 [ 称为二端口的Y 参数矩阵,属于 导纳性质。 2010年3月3日星期三 8
2010年3月3日星期三 8 结束 §16-2 二端口的方程和参数 一、Y(导纳)参数方程及Y参数 2. Y(导纳)参数 . I 1 . I 2 . U1 . U2 . I1 = Y11 . U1 + Y12 . U2 . I2 = Y21 . U1 + Y22 . U2 . I 1 . I 2 . U1 (1) (1) . I 1 . I 2 . U2 (2) (2) . I 1 . I 2 . U1 . U2 写成矩阵形式: . I1 . I2 = Y11 Y12 Y21 Y22 . U1 . U2 =Y . U1 . U2 Y def Y11 Y12 Y21 Y22 称为二端口的Y 参数矩阵,属于 导纳性质。 1. 方程 由于是线性二端口, 故用叠加原理可得

3.Y参数的含义与求法 端口1-1' i,=Y11U+Y12U2 短 Y11 的短路输 结束 11U=0 入导纳 i2=Y21U1+Y22U2 路 法 口2短路,2 √给定实际电路(结构 Y1= ,=0 与1之间的 参数可能未知), i 转移导纳 Y22 20=0 口1短路,1 与2之间的 U1=0 U Y22= 转移导纳 V, 0,=0 先通过实验测定端口 端口2-2的短路输入导纳 电流与电压,再经过 当电路的结构参数已知时, 简单计算即可。 直接按定义分析计算: 2010年3月3日星期三 9
2010年3月3日星期三 9 结束 = 0 3. Y参数的含义与求法 给定实际电路(结构 参数可能未知), 当电路的结构参数已知时, 直接按定义分析计算: . I 1 . I 2 . U1 . U2 . I1 = Y11 . U1 + Y12 . U2 . I2 = Y21 . U1 + Y22 . U2 先通过实验测定端口 电流与电压,再经过 简单计算即可。 Y11 = . I1 . U1 . U2=0 Y21 = . I2 . U1 . U2=0 = 0 . I 1 . I 2 . U1 . U2 Y12 = . I1 . U2 . U1=0 Y22 = . I2 . U2 . U1=0 端口1-1' 的短路输 入导纳 端口2-2'的短路输入导纳 口2短路,2 与1之间的 转移导纳 短 路 法 口1短路,1 与2之间的 转移导纳
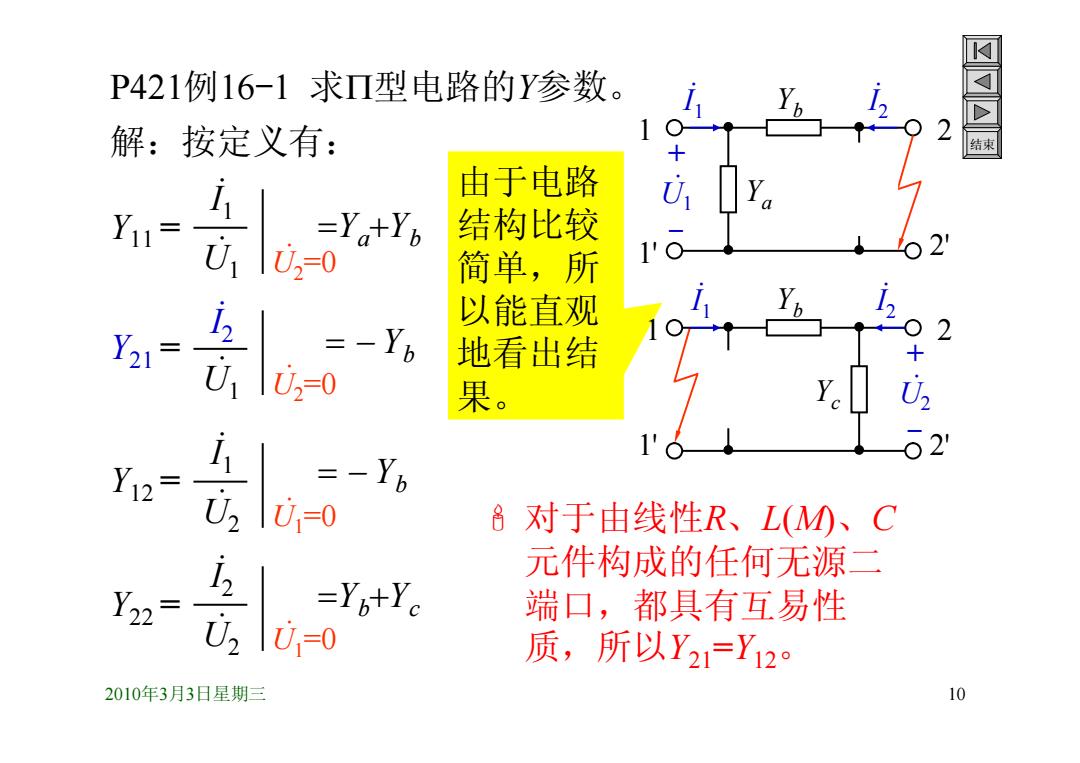
P421例16-1求Π型电路的Y参数。 解:按定义有: 结束 由于电路 a Yu=- =Ya+Yb 结构比较 2 简单,所 以能直观 Y21= =-Yb 地看出结 U2=0 果。 心2 i 2 =-Yb V, U=0 8对于由线性R、L(M、C Y22= i 元件构成的任何无源二 =Yp+Yc 端口,都具有互易性 V, U=0 质,所以Y21=Y120 2010年3月3日星期三 10
2010年3月3日星期三 10 结束 P421例16-1 求型电路的Y参数。 解:按定义有: 对于由线性R、L(M)、C 元件构成的任何无源二 端口,都具有互易性 质,所以Y21 =Y12。 1 1' 2 2' Ya Yb Yc Y11 = . I1 . U1 . U2=0 Y21 = . I2 . U1 . U2=0 . I 2 + - . U1 . I 1 由于电路 结构比较 简单,所 以能直观 地看出结 果。 YaYb Yb 1 1' 2 2' Ya Yb Yc . I 2 + - . U2 . I 1 Y12 = . I1 . U2 . U1=0 Yb Y22 = . I2 . U2 . U1=0 YbYc