海南大学：《电路原理》课程教学资源（课件讲稿）正弦稳态习题

第八章第九章 要点：1.正弦量的基本概念：三要素、相位差、波 形. 2.定量计算：相量法 辅助工具：相量图 3功率计算：有功、无功、视在功率、功率因数、 复功率等

第八章 第九章 要点：1. 正弦量的基本概念：三要素、相位差、波 形… 2. 定量计算：相量法 辅助工具：相量图 3.功率计算：有功、无功、视在功率、功率因数、 复功率等

一.正弦量、相量的基本概念 左图电路中，已知： 1、 u(t)=10cos(400元t+60°)V L 0z=|z∠9 0)=2 in(400πt-150°)A (a)电源电压角频率o=400元rad/s,频率=200Hz,周期T=0.005s (b)电压有效值U=7.07V,电流有效值= 0.5A (c)电压、电流间相位差平。平，=120 (d该负载是感性负载，☑=14.142 ,9= 120°

一. 正弦量、相量的基本概念 左图电路中，已知： sin( 400π 150 ) A 2 1 ( ) ( ) 10 cos(400 60 ) V        i t t u t πt 1、 400 rad/s 200Hz 0.005s 7.07V 0.5A  120 感性 14.14 i + u Z  Z φ – (a)电源电压角频率 =_________ , 频率 f=_____ , 周期 T=_______. (b)电压有效值U=_______，电流有效值 I=________. (c)电压、电流间相位差 u– i =_________. (d)该负载是______负载, |Z|=_________,  =_________.  120

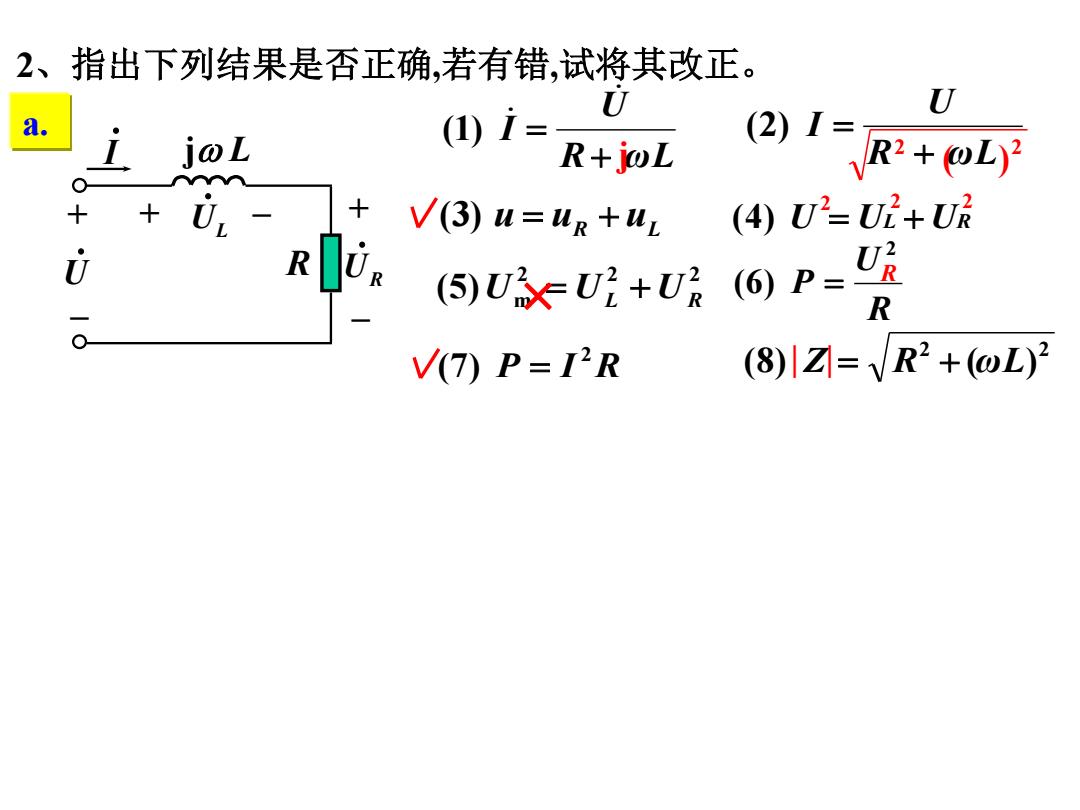
2、指出下列结果是否正确，若有错，试将其改正。 U U a. i (1)1= R+j@L 21=R2+ob 十 V(3)u=uR+uL (4)U2=U+UR R U: (⑤)UxU2+UR(⑥)P= R V(7)P=IR (8)川☑=VR+@L)2

2、指出下列结果是否正确,若有错,试将其改正。 R ωL U I (1)     (2) R ωL U I   u  uR  uL (3) (4) U  UL  UR 2 2 2 m (5)U  UL  UR R U P 2 (6)  P I R 2 (7)  2 2 (8) Z  R  (ωL) a. R 2 2 2 j R j L + –  U  I  UL + – + –  UR 2 2 ( )  | |

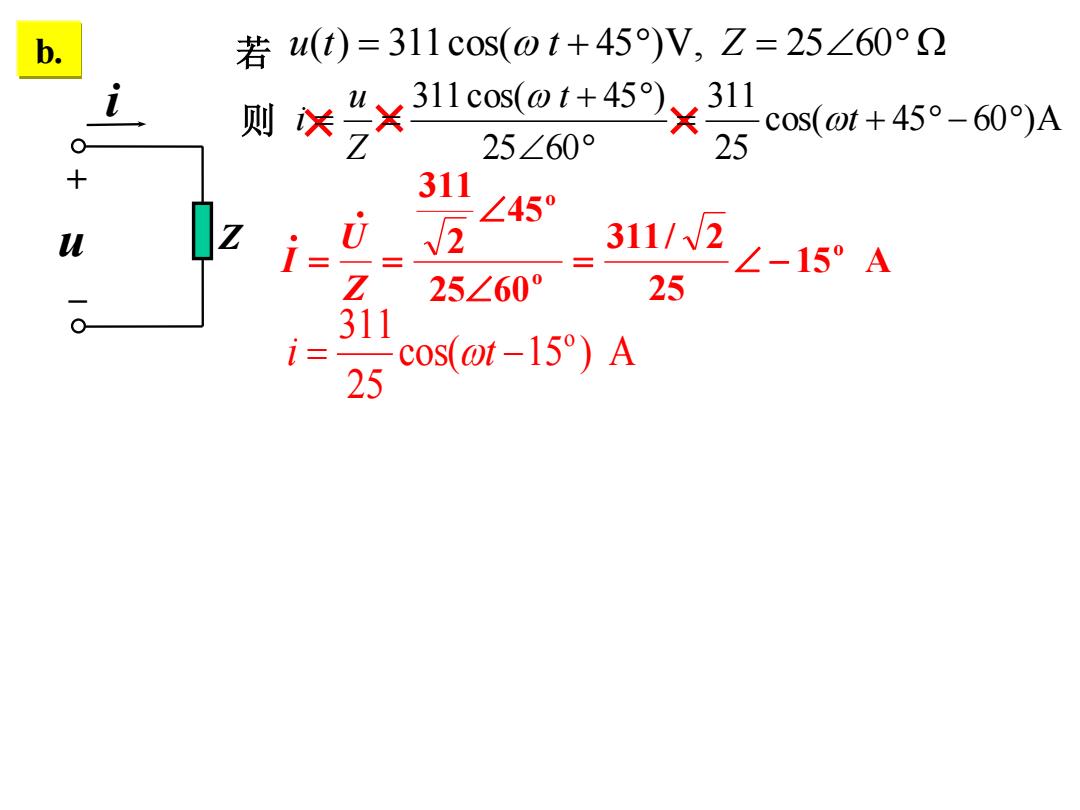
b. 若u(t)=311c0s(0t+45)V,Z=25∠60°2 则关 + 11c0s(ot+45)、311 -C0s(ot+45°-60)A 25∠60° 25 + 311 ∠45° L Z i 311/V2 一 ∠-15°A 25∠60° 25 311 i= cos(@t-15)A 25

若 u(t)  311cos(  t  45 )V, Ζ  25 60  Ω 则 b.    cos( 45 60 )A 25 311 25 60 311cos( 45 )           t t Zu i   u Z i +– 15 A 25 311/ 2 25 60 45 2 311 o o o         ZU I cos( 15 ) A 25 311 o i  t 

用相量法分析正弦稳态电路的基本步骤： ()时域电路-〉相量模型 a:u,i的相量形式 b:各元件的阻抗 根据电路的结构特点，选用合适的分析方法，求出待求变量 的相量 根据求得的相量，写出其时域表达式

用相量法分析正弦稳态电路的基本步骤： (1) 时域电路--------〉相量模型 a：u,i 的相量形式 b：各元件的阻抗 • 根据电路的结构特点，选用合适的分析方法，求出待求变量 的相量 • 根据求得的相量，写出其时域表达式

正弦稳态电路的功率分析： 有功功率：P=UIcosp 单位：W S 视在功率：S=U 单位：VA 2 无功功率：Q=UIsinp 单位：var P=Scoso, O=S sin o 功率三角形 S=Vp+O,0=aretand号)

有功功率: P=UIcos 单位：W 无功功率: Q=UIsin 单位：var 视在功率: S=UI 单位：VA  S P Q 功率三角形 , arctan( ) cos , sin 2 2 P Q S P Q P S Q S         正弦稳态电路的功率分析：

已知：已知电流表读数为1.5A(有效值)。 求：(1)U、=？(2)电路吸收的有功功率P和无功功率Q. 402 24182 U 1广j302 -j502— 解：设iR=1.5∠0°A 则02=40×1.5∠0°=60∠0°V 02=2∠90°=j2A ic=-j30 i=iR+ic=1.5+j2=2.5∠53.1A U1=(24+j18)1=(24+j18)×2.5∠53.1°=75∠90°=j75V U3=(-j50)1=(-j50)×2.5∠53.1°=125∠-36.9°=100-j75V

已知：已知电流表读数为1.5A(有效值)。 求：(1)US=? (2)电路吸收的有功功率P和无功功率Q . A 24Ω j18Ω 40Ω  j30Ω  j50Ω + –  US  I  U 2  U3  C  I U1 + + – –  R I + – 解： 1.5 0 A  设 I  R   2 40 1.5 0 60 0 V   则 U       2 90 j2A j30 2         U IC 1.5 2 2.5 53.1 A  I   I  R  I  C   j   1  (24  j18)  (24  j18) 2.553.1  7590  j75V     U I 3  (j50)  (j50) 2.553.1  125  36.9  100  j75V     U I

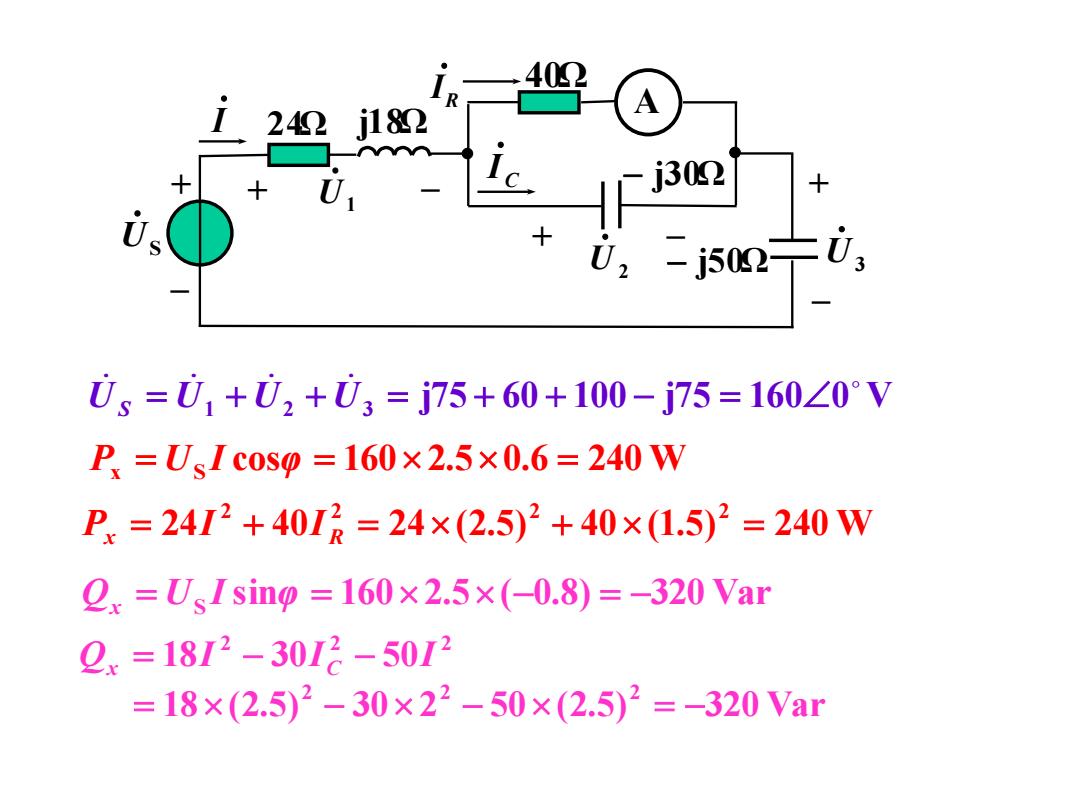
IR 402 I242j182 A X U 1广j302 十 U. 0,-j5020， 0,=01+02+03=j75+60+100-j75=160∠0V P=UsIc0s0=160×2.5×0.6=240W P.=24I2+40IR=24×(2.5)2+40×(1.5)2=240W 2.=UsI sing0=160×2.5×(-0.8)=-320Var 2.=18I2-30I2-50I2 =18×(2.5)2-30×22-50×(2.5)2=-320Vam

1 2 3 j75 60 100 j75 160 0 V U S  U  U  U       Px  US I cosφ  160 2.50.6  240 W sin 160 2.5 ( 0.8) 320 Var Qx  US I φ       Px  24I 2  40I R2  24(2.5)2  40(1.5)2  240 W 18 (2.5) 30 2 50 (2.5) 320 Var 18 30 50 2 2 2 2 2 2         Q  I  I  I x C A 24Ω j18Ω 40Ω  j30Ω j50Ω +–  U S  I  U 2  U3 C  I U1 + + – – RI + –

己知：0s1=110L-30V,0s2=110∠30°V, L=1.5H,f=50Hz. 试求：两个电源各自发出的有功功率 和无功功率。 解：i-0-U 2_110∠-30°-110∠30°-j110 =-0.234A joL j314×1.5 j471 P1=Us1Ic0s(-30°-180°)=110×0.234×(-0.866)=-22.3W 21=Us1Isin(-30°-180)=110×0.234×0.5=12.9Var P2=-V2Ic0s(30°-180)=-110×0.234×(-0.866)=22.3W 22=-Us2Isin(30°-180)=-110×0.234×(-0.5)=12.9Var 两个电源发出的有功功率互相抵消，而无功功率不 抵消，因为电路中的电感吸收无功

已知： 1.5H, 50Hz. 110 30 V, 110 30 V, S1 S2        L f U U     试求：两个电源各自发出的有功功率 和无功功率。 解： 0.234 A j471 j110 j314 1.5 110 30 110 30 j 1 S1 S2                  ωL U U I P1  US1 I cos(30  180 )  1100.234(0.866)  22.3 W sin( 30 180 ) 110 0.234 0.5 12.9 Var 1  S1         Q U I P2  US2 I cos(30  180 )  110 0.234(0.866)  22.3 W sin(30 180 ) 110 0.234 ( 0.5) 12.9 Var 2   2          Q U I S 两个电源发出的有功功率互相抵消，而无功功率不 抵消，因为电路中的电感吸收无功。 L US1  US 2  I  + – + –