海南大学：《电路原理》课程教学资源（课件讲稿）第十章 含有耦合电感的电路

第十章 含有耦合电感的电路 主要内容： 1、互感 2、含有耦合电感电路的分析计算 3、理想变压器

第十章 含有耦合电感的电路 2、含有耦合电感电路的分析计算 1、互感 3、理想变压器 主要内容：

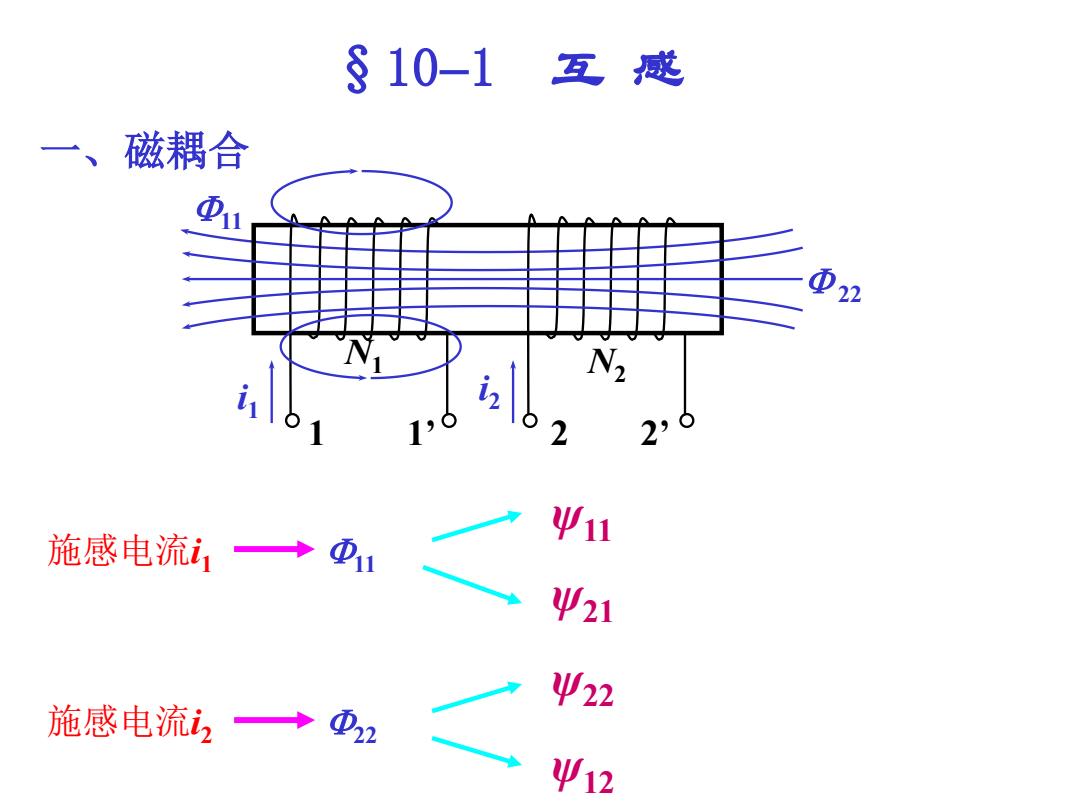
§10-1。 互感 一、磁耦合 ①11 N2 16 2,6 施感电流i1→D Ψ11 Ψ21 Ψ22 施感电流，→D2 Ψ12

一、磁耦合 §101 互 感 1 1’ 2 2’ i1 11  22 N1 N2 i2 施感电流i1 11 ψ11 ψ21 22 ψ22 ψ12 施感电流i2

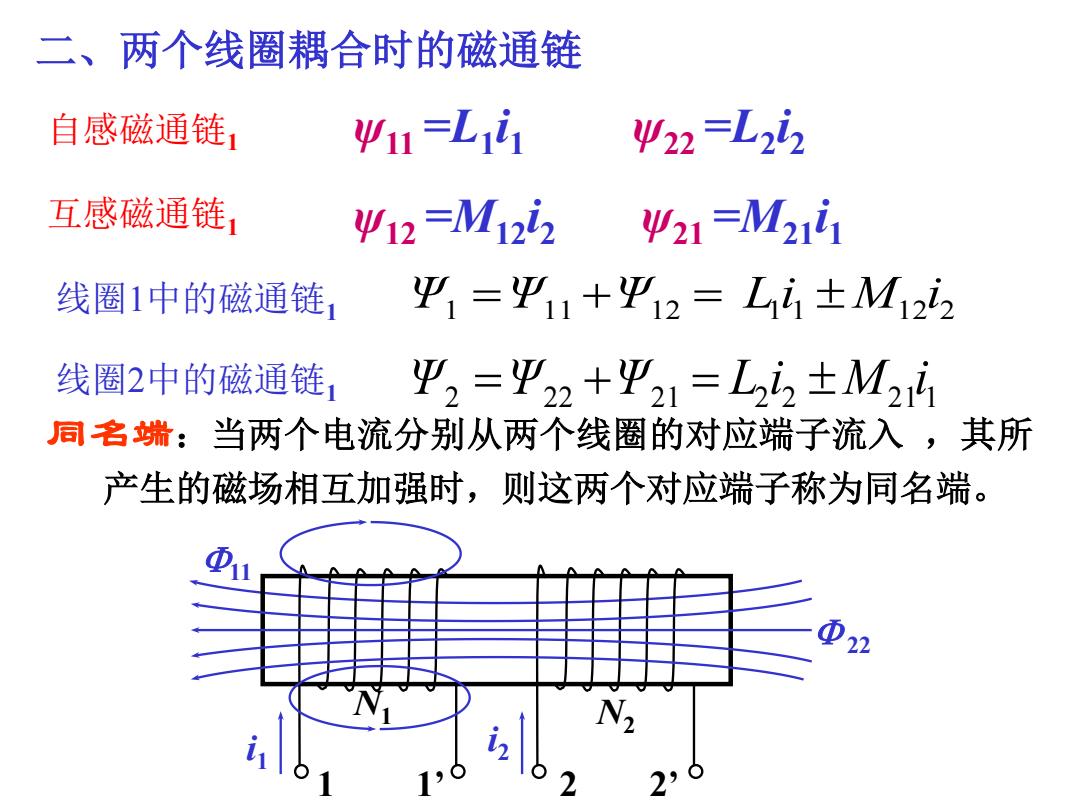
二、两个线圈耦合时的磁通链 自感磁通链， 411=L11 422=L22 互感磁通链， 412=M122 421=M21i1 线圈1中的磁通链， 平1=平1+平12=Li1±M122 线圈2中的磁通链1， 平2=Ψ22+平21=L22±M24 同名端：当两个电流分别从两个线圈的对应端子流入，其所 产生的磁场相互加强时，则这两个对应端子称为同名端。 ①2

二、两个线圈耦合时的磁通链 自感磁通链1 ψ11 =L1 i1 ψ22 =L2 i2 互感磁通链1 ψ12 =M12i2 ψ21 =M21i1 线圈1中的磁通链1 线圈2中的磁通链1 1 11 12 1 1 12 2 Ψ Ψ Ψ  Li  M i 2 22 21 2 2 21 1 Ψ Ψ Ψ  L i  M i 同名端：当两个电流分别从两个线圈的对应端子流入 ，其所 产生的磁场相互加强时，则这两个对应端子称为同名端。 1 1’ 2 2’ i1 11  22 N1 N2 i2

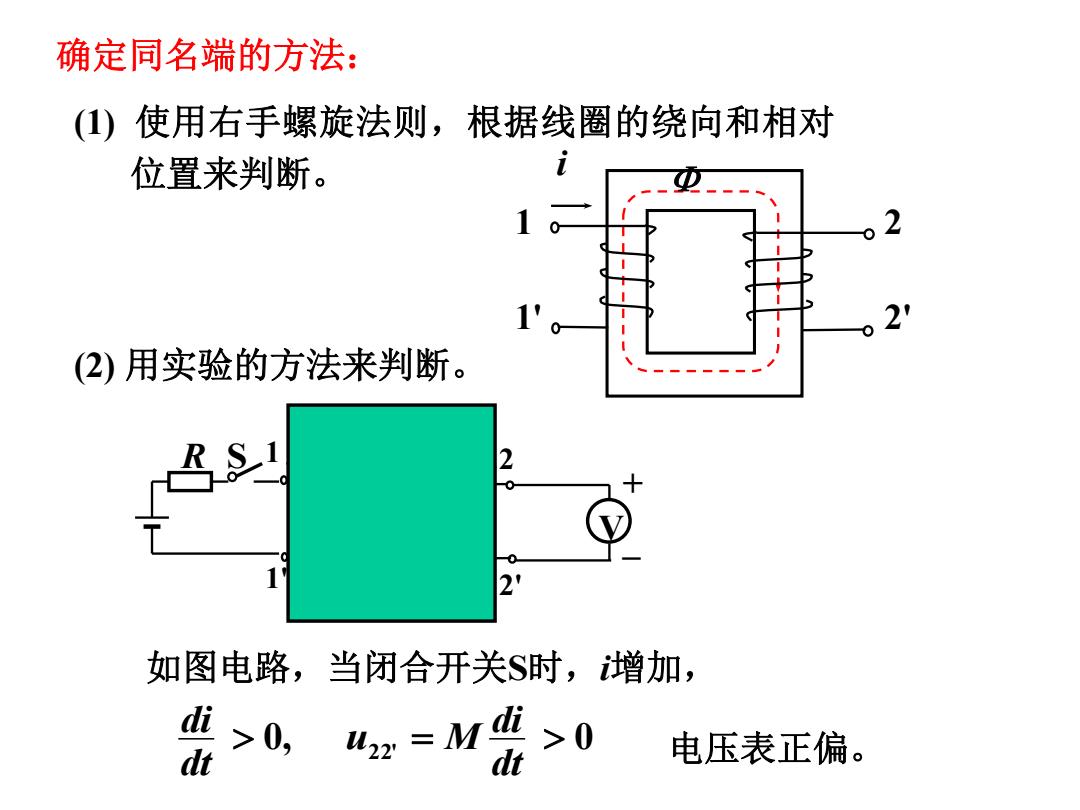
确定同名端的方法： (1)使用右手螺旋法则， 根据线圈的绕向和相对 位置来判断。 (2)用实验的方法来判断。 如图电路，当闭合开关S时，增加， di >0,42z=M >0 dt dt 电压表正偏

确定同名端的方法：  i 1 1' 2 2' (1) 使用右手螺旋法则，根据线圈的绕向和相对 位置来判断。 (2) 用实验的方法来判断。 i 1 1' 2 2' * * R S V + –  0, 2 2'  dt  0 电压表正偏。 M di u dt di 如图电路，当闭合开关S时，i增加

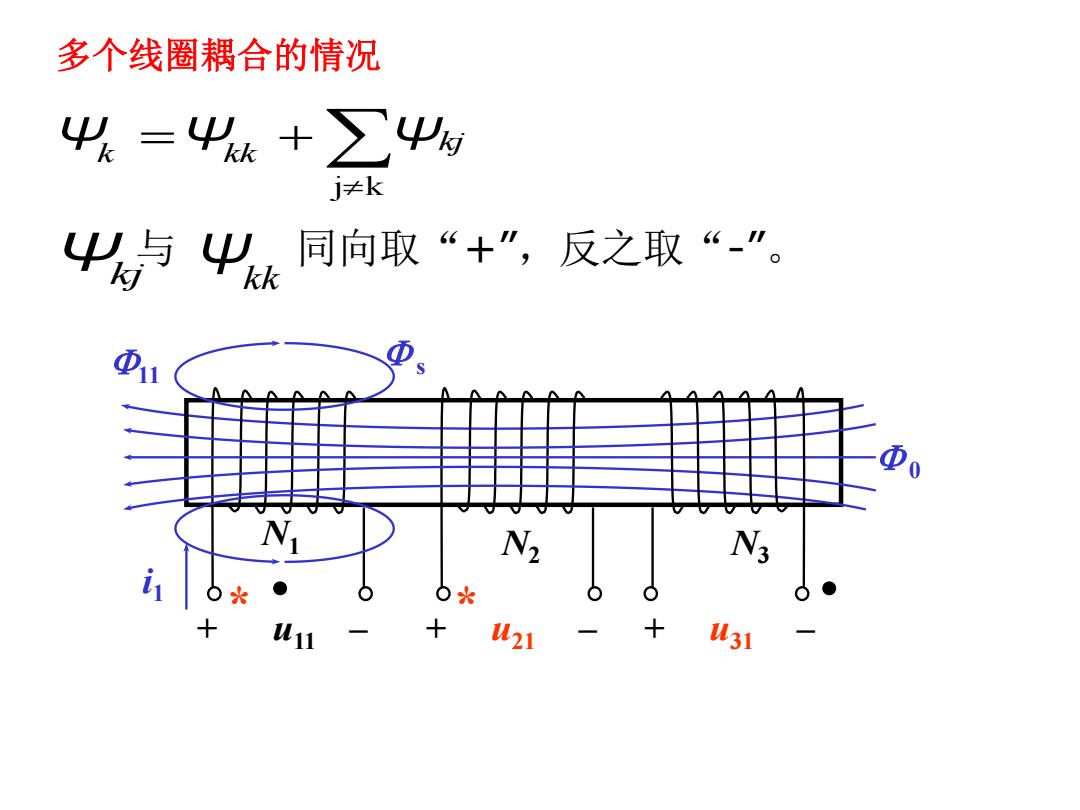
多个线圈耦合的情况 4=4k+∑∑4g j≠k Ψ4 同向取“+”，反之取“-”。 ①1 N2 N 0水 十 W11 十 W21 U31

多个线圈耦合的情况     j k kj Ψk Ψkk Ψ 与 同向取“+”，反之取“-” 。 Ψkj Ψkk + u11 – + u21 – i1 11  0 N1 N2 + u31 – N3  s * *  

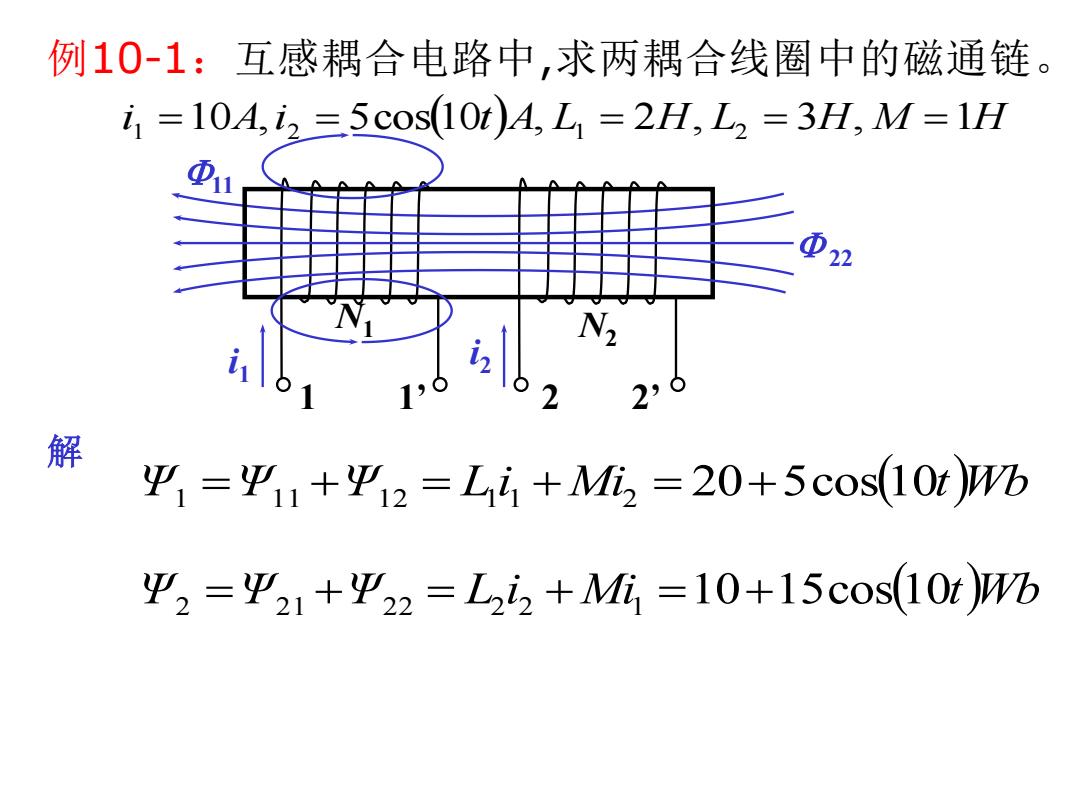
例10-1：互感耦合电路中，求两耦合线圈中的磁通链 i1=10A,i2=5cos10t)A,L1=2H,L2=3H,M=1H ①2 N2 136 2 29 解 g=平1+乎12=L4+M=20+5cos(10t)W% Y平2=平21+平22=L2i2+M=10+15cos(10t)W%

例10-1：互感耦合电路中,求两耦合线圈中的磁通链。 i 1 10A,i 2  5cos10tA, L1  2H, L2  3H, M 1H Ψ1 Ψ1 1 Ψ1 2  L1 i 1  Mi2  205cos10tWb Ψ2 Ψ2 1 Ψ2 2  L2 i 2  Mi1 1015cos10tWb 解 1 1’ 2 2’ i1 11  22 N1 N2 i2

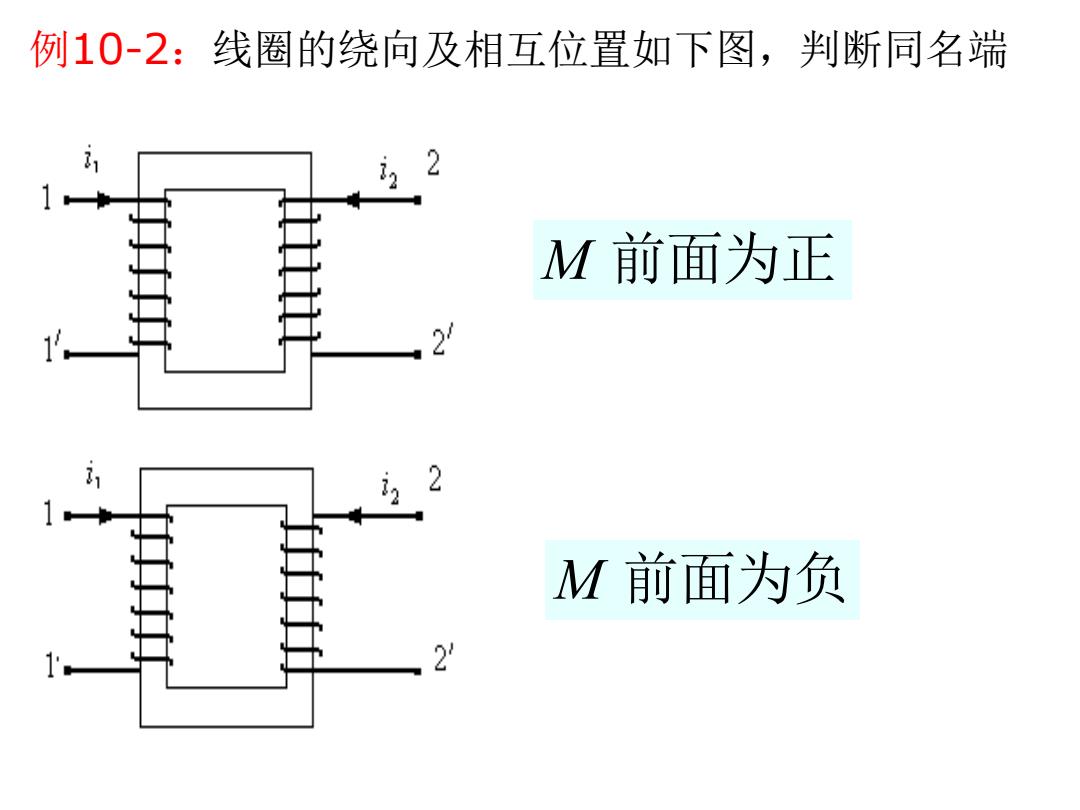
例10-2：线圈的绕向及相互位置如下图，判断同名端 M前面为正 M前面为负

例10-2：线圈的绕向及相互位置如下图，判断同名端 M 前面为正 M 前面为负

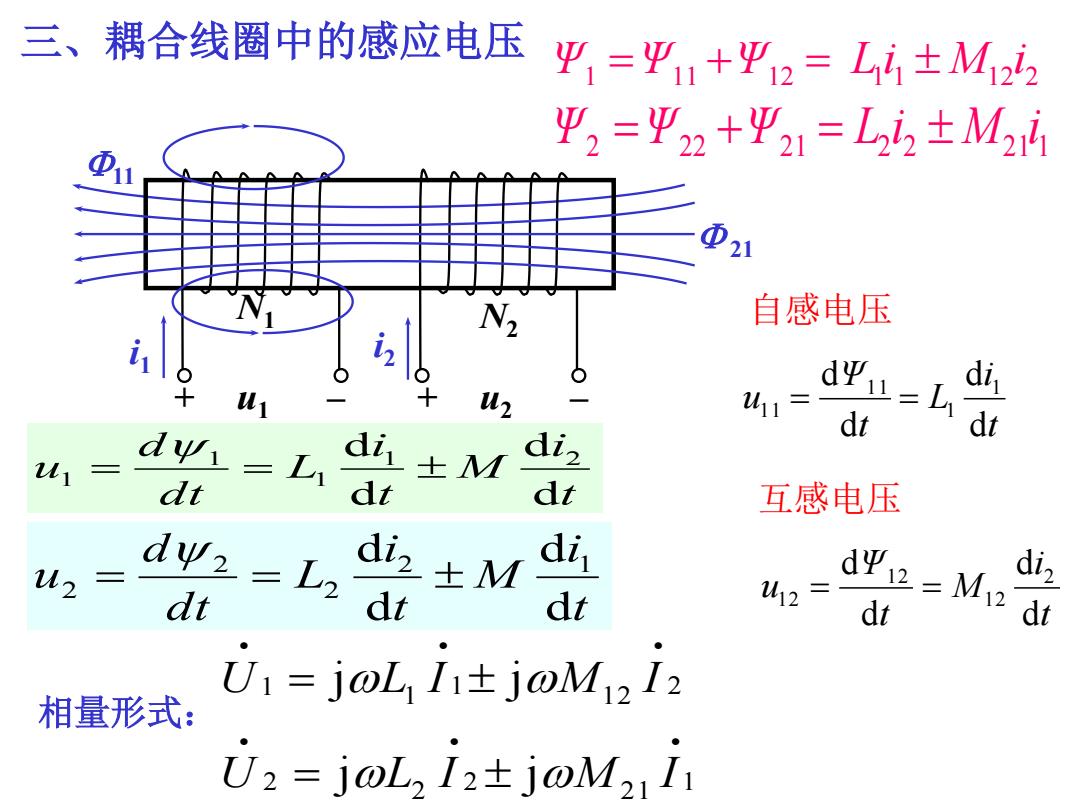
三、耦合线圈中的感应电压 Ψ1=平1+Ψ2=L4±M122 Ψ2=Ψ2+Ψ21=L22±M2 N 自感电压 u uz u11= dΨu-L dt dt 1 三 d' ±M di dt dt dt 互感电压 M2= d2二L2 diz ±M di dt dt dt 42 dΨ2-M2 dt dt U1=joL,1±joM2i2 相量形式： U2=joL2I2±joM21i1

三、耦合线圈中的感应电压 1 11 12 1 1 12 2 Ψ Ψ Ψ  Li  M i 2 22 21 2 2 21 1 Ψ Ψ Ψ  L i  M i 1 2 1 2 2 2 2 1 2 1 1 1 j j j j           U L I M I U L I M I     t i M t i L dt d u d d d d 2 1 2 2 2     t i M t i L dt d u d d d d 1 2 1 1 1     相量形式： 自感电压 互感电压 t i L t Ψ u d d d d 1 1 1 1 1 1   t i M t Ψ u d d d d 2 1 2 1 2 1 2   + u1 – + u2 – i1 11  21 N1 N2 i2

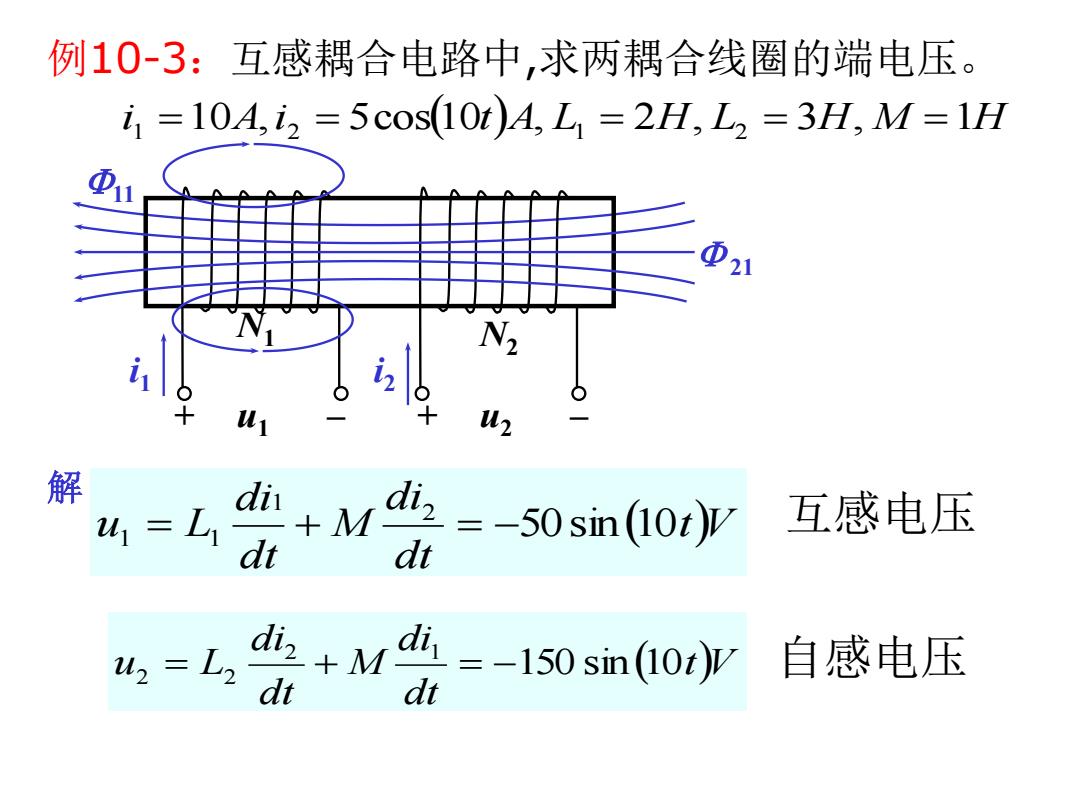
例10-3：互感耦合电路中，求两耦合线圈的端电压。 i,=10A,i2=5cos10t)A,L1=2H,L2=3H,M=1H N2 解 u1=L1 di dt +M,=-50sin(10）y 互感电压 dt u2=L2 iz+M osam0y 自感电压

例10-3：互感耦合电路中,求两耦合线圈的端电压。 i 1 10A,i 2  5cos10tA, L1  2H, L2  3H, M 1H 解 + u1 – + u2 – i1 11  21 N1 N2  tV 互感电压 dt di M dt di u L 50sin 10 2 1 1  1     tV dt di M dt di u L 150 sin 10 2 1 2  2    自感电压 i2

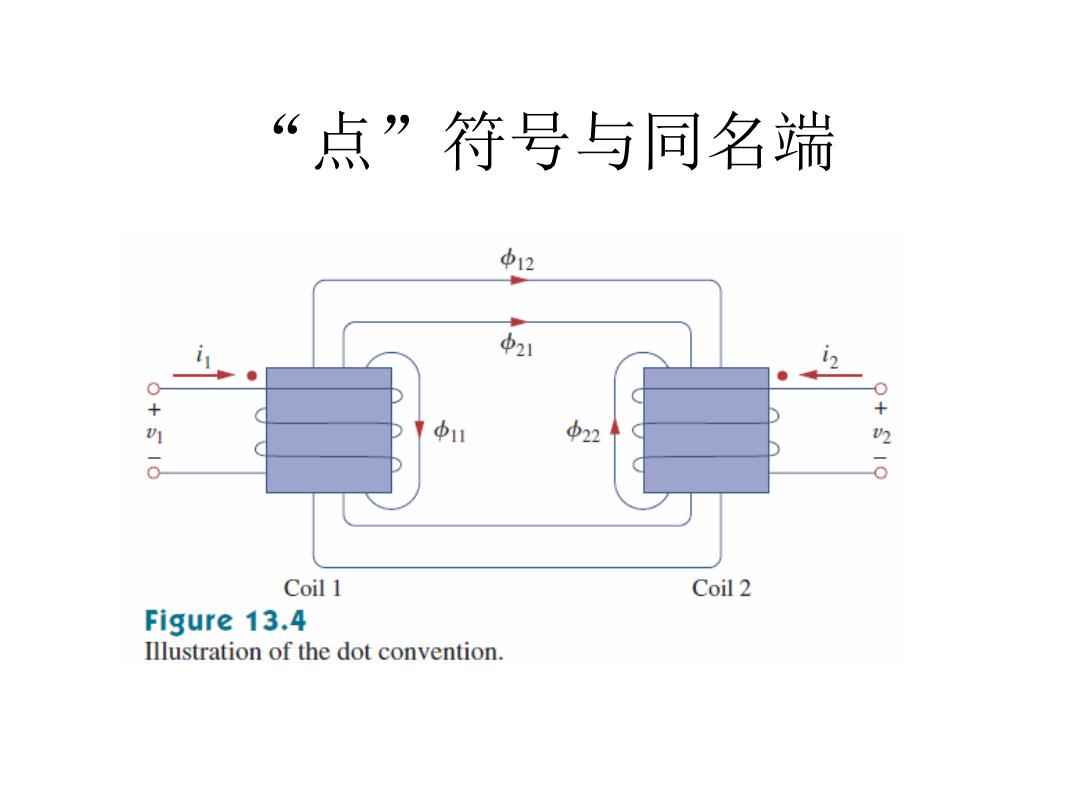
“点”符号与同名端 2 21 ● + + 中11 2 0 Coil 1 Coil 2 Figure 13.4 Illustration of the dot convention

“点”符号与同名端