海南大学：《电路原理》课程教学资源（课件讲稿）第十一章 电路的频率响应

第十一章 电路的频率响应 主要内容： 1、网络函数等概念 2、串联电路的谐振 3、并联谐振电路

第十一章 电路的频率响应 1、网络函数等概念 2、串联电路的谐振 主要内容： 3、并联谐振电路

§11-1 网络函数 频率响应： 电路和系统的工作状态跟随频率而变化的现象， 称为电路和系统的频率特性，又称频率响应。 网络函数： 通常在输入变量和输出变量之间建立“一对一” 的函数关系，描述电路的频率特性，这一函数称 为电路和系统的网络函数。 定义： 网络函数 H(@)= Rkω) Rk (jo) Esi(jo) 输出端口k的响应 EyGjω) 输入端口j的响应输入变量

频率响应： §111 网络函数 定义： 电路和系统的工作状态跟随频率而变化的现象， 称为电路和系统的频率特性，又称频率响应。 ) ) ) E (jω R (jω H(jω s j k    网络函数： 通常在输入变量和输出变量之间建立“一对一” 的函数关系，描述电路的频率特性，这一函数称 为电路和系统的网络函数。 网络函数 Rk (jω)  Esj (jω)  输出端口k的响应 输入端口j的响应输入变量

多种类型的网络函数： 阻抗 导纳 1.响应和激励位于同一端口：H(Go)即 或 ix I sk Usk 2.响应和激励位于不同端口：H(Gw)称为转移函数 转移 Ik 转移电 转移 Ux 转移电 阻抗 Isi 流比 导纳 压比 H(jo)一o 幅频特性 p(jo)-w 相频特性

s k k s k k H(j )     U I I U 1.响应和激励位于同一端口：  即 或 阻抗 导纳 多种类型的网络函数： 2.响应和激励位于不同端口： H(j)称为转移函数 sj k   I U sj k   I I sj k   U U sj k   U 转移 I 阻抗 转移电 流比 转移 导纳 转移电 压比 | H(j)| — (j) — 幅频特性 相频特性

§11-2 串联电路的谐振 一、RLC串联电路的谐振现象 R Z-R+j@L-a)-R+jx.+Xc)qZ126 当wL> 即XL>-XG 感性 1 当d< 即X<-Xc 容性 Xi(@) X(@) 当满足一定条件（对RLC串 联电路，使oL=1/oC,电 路中电压、电流同相，电路 Xdo) 的这种状态称为谐振

X( ) XL ( ) XC ( )  0  Z ( ) O §112 串联电路的谐振 一、RLC串联电路的谐振现象    )   j(  ) | |  1 j( R X X Z ωC Z R ωL L C 当 , 即 感性 1 XL XC ωC ωL     I R j L + _ jωC 1  U 当 , 即 容性 1 XL XC ωC ωL    当满足一定条件(对RLC串 联电路，使 L=1/ C)， 电 路中电压、电流同相，电路 的这种状态称为谐振

串联谐振：w,L=。C 谐振角频率 LC 谐振频率 二、使RLC串联电路发生谐振的条件 1.LC不变，改变0。 2.电源频率不变，改变L或C(常改变C)

串联谐振： 二、使RLC串联电路发生谐振的条件 1. L C 不变，改变  。 2. 电源频率不变，改变 L 或 C ( 常改变C )。 谐振角频率 LC ω 1 0  谐振频率 LC f 2π 1 0  C ω L 0 0 1  

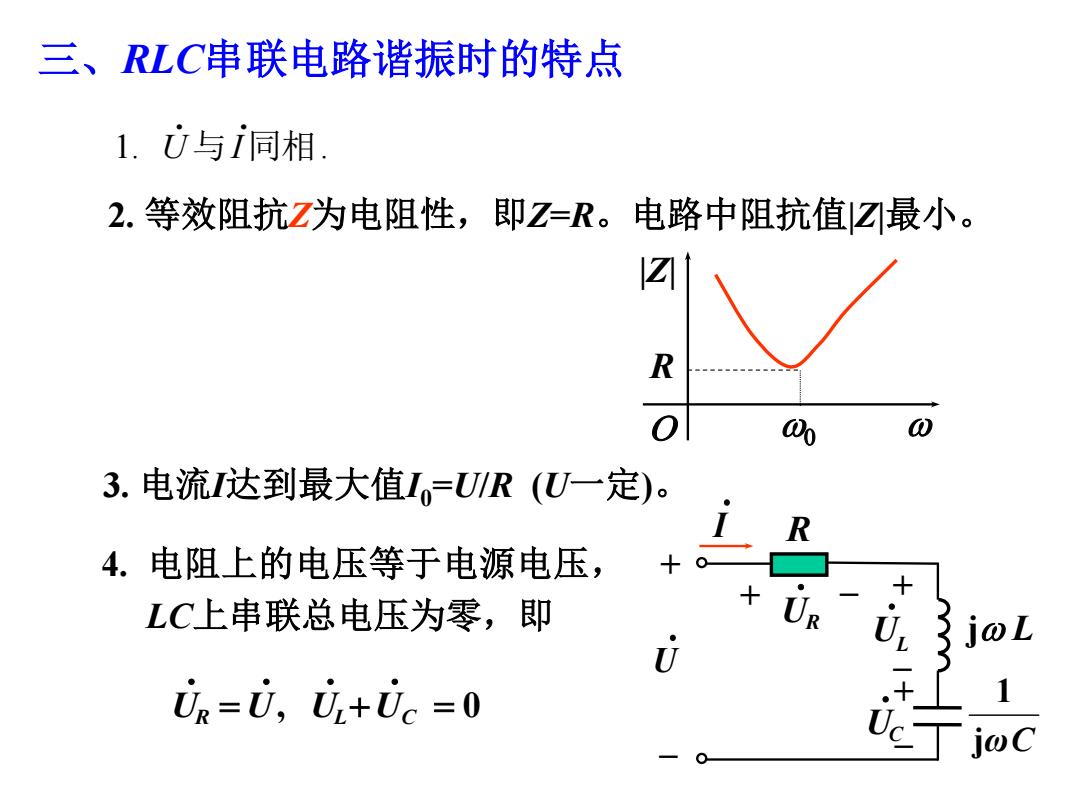
三、RLC串联电路谐振时的特点 1.U与同相. 2.等效阻抗Z为电阻性，即Z=R。电路中阻抗值☑最小。 Z☑1 R 0 00 0 3.电流I达到最大值I=U/R(U一定)。 R 4.电阻上的电压等于电源电压， LC上串联总电压为零，即 U Vg=V,U+Uc =0 Q

三、RLC串联电路谐振时的特点 1. . 与 同相   U I 2. 等效阻抗Z为电阻性，即Z=R。电路中阻抗值|Z|最小。 |Z| O 0  R 3. 电流I达到最大值I0 =U/R (U一定)。  I R j L + _ jωC 1  U + + + _ _ _ UR  UL  UC   ,   0     UR U UL UC 4. 电阻上的电压等于电源电压， LC上串联总电压为零，即

串联谐振时，电感上的电压和 0, 电容上的电压大小相等，方向相反， 湘互抵消，因此串联谐振又称电压 谐振。 ni Ve 5.功率 P=RI=U/R g=g,+Q=0g.=a,u.0,=c1 即L与C交换能量，与电源间无能量交换

串联谐振时，电感上的电压和 电容上的电压大小相等，方向相反， 相互抵消，因此串联谐振又称电压 谐振。 UL  UC  UR   I 5. 功率 P=RI0 2=U2 /R 即L与C交换能量，与电源间无能量交换。 2 0 0 2 0 0 1 0, , I ω C Q  QL  QC  QL  ω LI QC  

四、品质因数 1.品质因数的定义 da-jo,Zi-限Ri=j0 R Uco=-1 jwC j@.CR oL 1 R @CR 2.品质因数的意义 a.电压方面：Uo=Uco=2U 2= U U

四、品质因数 1.品质因数的定义          U ω CR R I ω C ω CR I UC 0 0 0 0 1 j j 1 j         U R ω L R I R ω L UL ω L I 0 0 0 0 j j j C L R CR R ω L Q 1 1 0 0     2.品质因数的意义 a.电压方面： UL0 = UC0 =QU U U U U Q L0 L0  

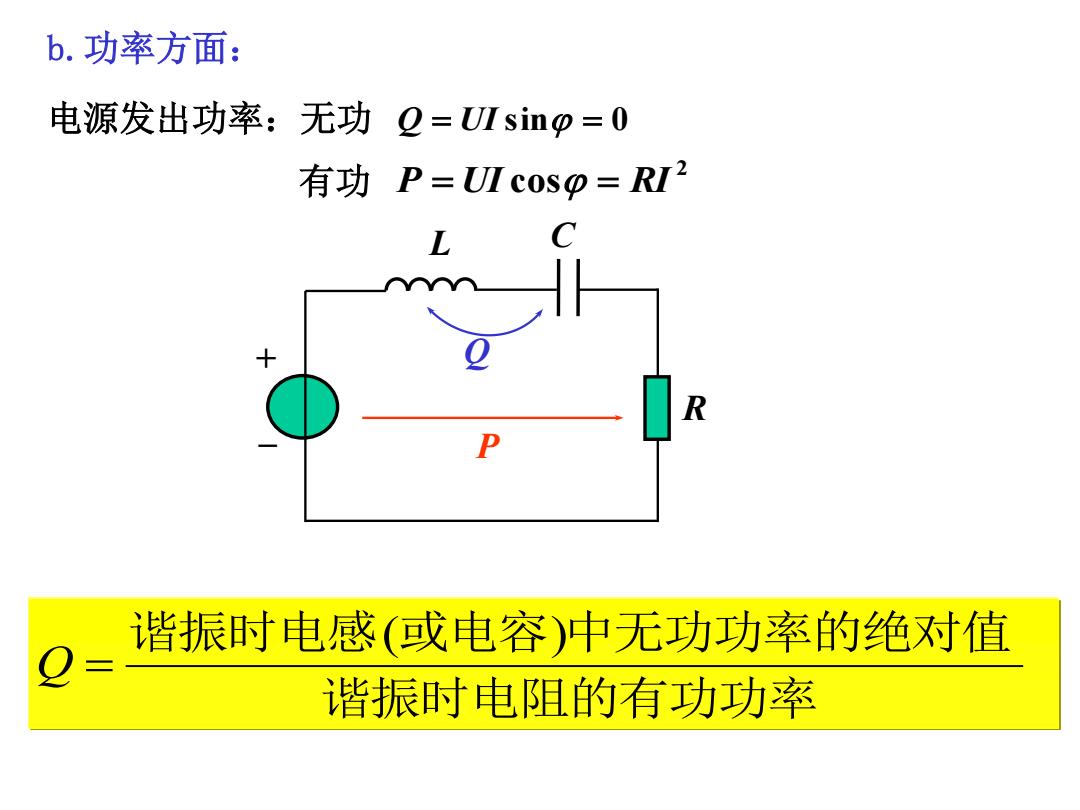
b.功率方面： 电源发出功率：无功2=UⅡsinp=0 有功P=UⅡcosp=RI2 谐振时电感（或电容）中无功功率的绝对值 谐振时电阻的有功功率

b.功率方面： 电源发出功率：无功 2 P  UI cos  RI Q  UI sin  0 有功 + _ P Q L C R ( ) 谐振时电阻的有功功率 谐振时电感 或电容 中无功功率的绝对值 Q 

c.能量方面： 谐振时电路中电磁场总储能 =2元 谐振时一周期内电路消耗的能量 L12 2πf6L 0=2πTR1f6 R 维持一定量的振荡所消耗的能量愈小， 则振荡电路的“品质”愈好

c.能量方面： 谐振时一周期内电路消 耗的能量 谐振时电路中电磁场总 储能 Q  2π 维持一定量的振荡所消耗的能量愈小， 则振荡电路的“品质”愈好