海南大学：《电路原理》课程教学资源（课件讲稿）第九章 正弦稳态电路的分析

第九章 正弦稳态电路的分析 主要内容： 1、阻抗、导纳的概念 2、电路的相量图 3、用相量法分析正弦稳态电路 4、正弦稳态电路中的功率分析

第九章 正弦稳态电路的分析 2、电路的相量图 1、阻抗、导纳的概念 3、用相量法分析正弦稳态电路 4、正弦稳态电路中的功率分析 主要内容：

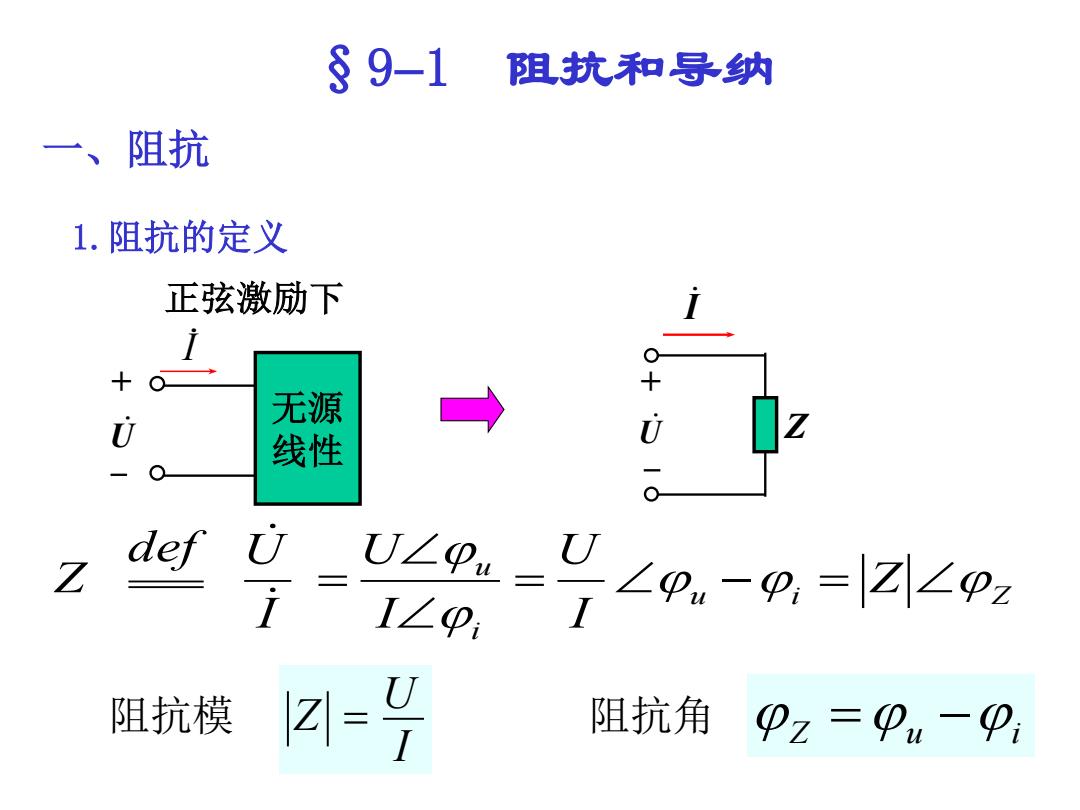
§9-1 阻抗和导纳 一、阻抗 1.阻抗的定义 正弦激励下 无源 → U 线性 U Z U∠9= i I∠p ∠0.-0，=Z201 阻抗模 4号 阻抗角 Pz=Pu一P

一、阻抗 §91 阻抗和导纳 1.阻抗的定义 正弦激励下 I  U  Z + - 无源 线性 I  U  + - u i Z i u Z I U I U I def U Z                阻抗模 I U Z  阻抗角  Z u i

2.阻抗的代数形式 U 阻抗Z= =Z|∠0z=R+jX I R=Re[Z]=Z coS pz 电阻 Iz X X=Im[Z]=Z sin z 电抗 R Z=R2+x2, 阻抗三角形 =arctan(R 若一端口N仅含单个元件 R: ZR-R L: Z. :,iωL 感 C: 容抗 w C

Z φ R X I U Z Z  | |    j   阻抗 2.阻抗的代数形式              Z Z X Z Z R Z Z   Im sin Re cos 电抗 电阻 , arctan( ) 2 2 R X Z  R  X  Z  若一端口N0仅含单个元件             ： 容抗 ： 感抗 ： C 1 C 1    j j C Z L Z j L R Z R C L R |Z| R X  阻抗三角形

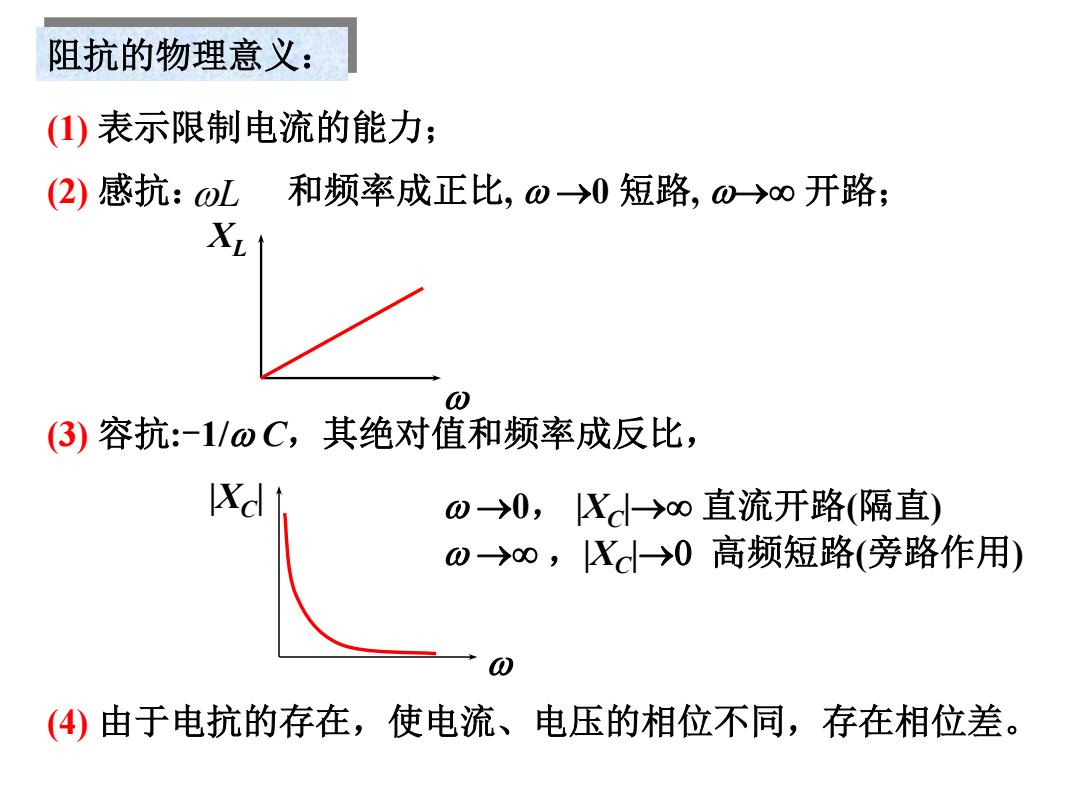
阻抗的物理意义： ()表示限制电流的能力： (2)感抗：oL 和频率成正比，ω→0短路，0→0开路； X (3)容抗：-1/oC,其绝对值和频率成反比， Xd ↑ 0-→0， Xd→o直流开路（隔直） 0→o，X→0高频短路（旁路作用） (4)由于电抗的存在，使电流、电压的相位不同，存在相位差

阻抗的物理意义： (1) 表示限制电流的能力； (4) 由于电抗的存在，使电流、电压的相位不同，存在相位差。  XL (2) 感抗： L 和频率成正比,  0 短路,  开路； (3) 容抗:-1/ C，其绝对值和频率成反比，  0， |XC | 直流开路(隔直)   ，|XC |0 高频短路(旁路作用)  |XC |

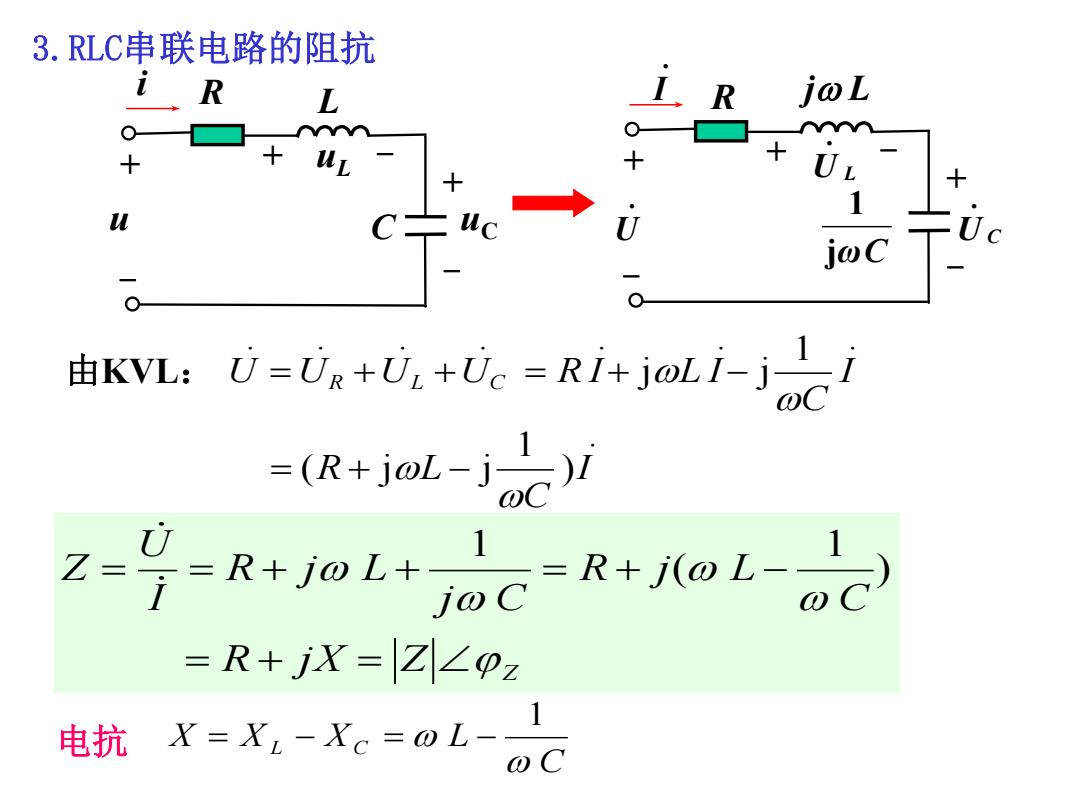
3.RLC串联电路的阻抗 iR L joL UL 1 L j@C KVL:Gi-tix+,+U.-Ri+jol.i- (R+jj U Z= =R+jX=Z∠pz 电抗 X=,-。=a-C

3.RLC串联电路的阻抗 L C R u uL uC i + - + - + - . I R j L + - + - + - . U U L . U C . jωC 1 由KVL： . ) 1 ( j j . 1 j . j . . . . . I C R L I C U U U UC R I L I R L              Z Z R j X C R j L j C R j L I U Z                 ) 1 ( 1   C X X L X C L 1  电抗     

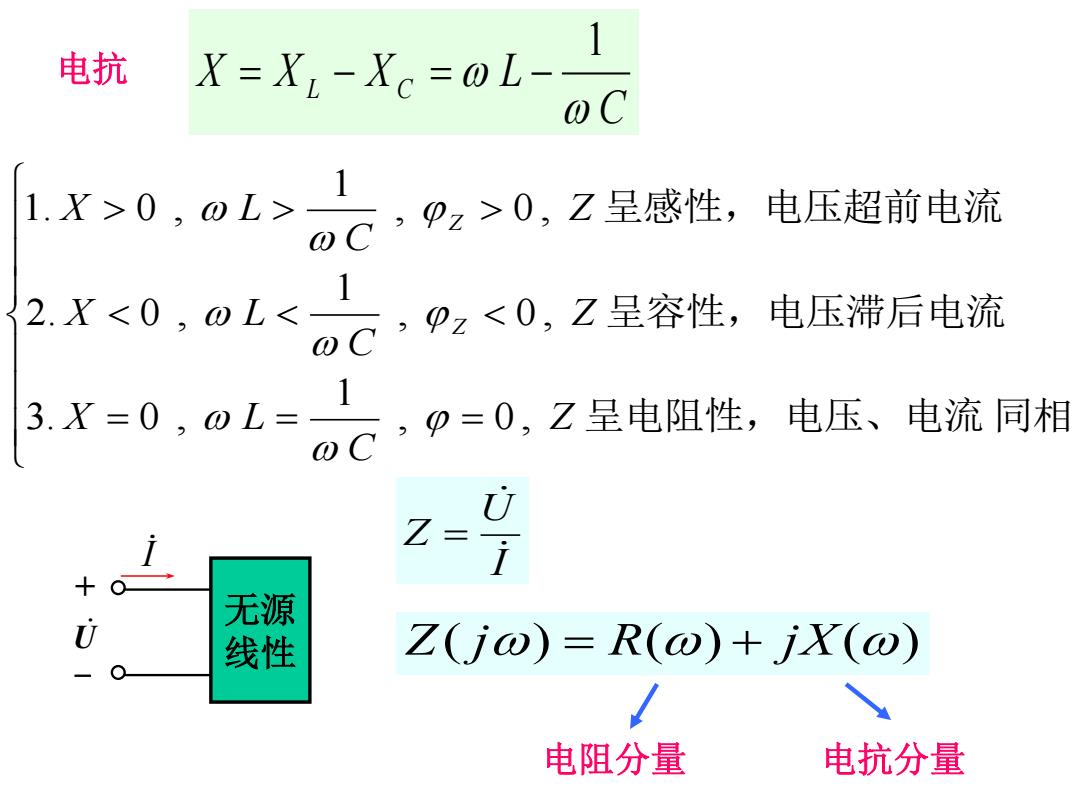
电抗 g=i-。=80 1X0,01>0C,,0,7呈感往， 电压超前电流 (<0,@L<。,pz<0,乙呈容性，电压滞后电流 X=0,0L=。C,p=0,Z呈电阻性，电压、电流月 U Z- 无源 U 线性 Z(jω)=R(ω)+jX(ω) 电阻分量 电抗分量

                  呈电阻性，电压、电流 同相 呈容性，电压滞后电流 呈感性，电压超前电流 , 0 , 1 3. 0 , , 0 , 1 2. 0 , , 0 , 1 1. 0 , Z C X L Z C X L Z C X L Z Z          C X X L X C L 1  电抗      无源 线性 I  U  + - I U Z    Z( j)  R()  j X() 电阻分量 电抗分量

二、导纳 1.导纳的定义 Y- U∠0，-.=Y∠9， 导纳模 Y 导纳角Py=P,一P, 2.导纳的代数形式 Y=- =zo,=G+8 G=Re[Y]=Ycos y电导 W B B=Im[Y]=Ysin ，电纳 G Y=G2+B2,p,arctan 导纳三角形 G

二、导纳 1.导纳的定义 i u Y y U I U I Z Y         1  导纳模 U I Y  导纳角  y i u 2.导纳的代数形式 Y G j B Z Y    y   1              y y B Y Y G Y Y   Im sin Re cos 电纳 电导 arctan 2 2          G B Y G B ， y |Y| G B  导纳三角形

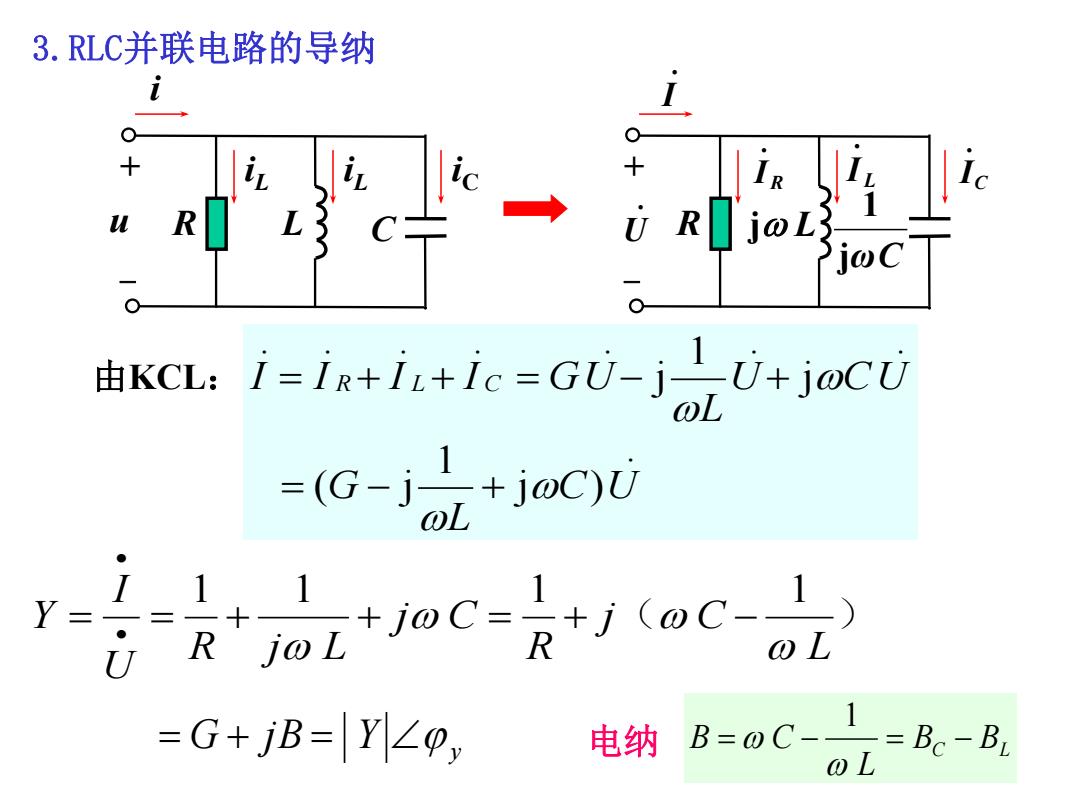
3.RLC并联电路的导纳 R 了jwC 由KCL:I=i++l=Gt-j+jo 5-jd+j00 ● I 1 1 Y 。 U =G+jB=Y∠0， 电纳8=oC--8

由KCL： i u R L C iL iC + - iL . I j L . U I L . IC . jωC 1 R + - I R . 3.RLC并联电路的导纳 . j ) 1 ( j . j . 1 j . . . . . C U L G U CU L I I R I L I C GU              1 1 1 1 （ ） L j C R j C R j L U I Y              Y y  G  j B   BC BL L B  C    1  电纳 

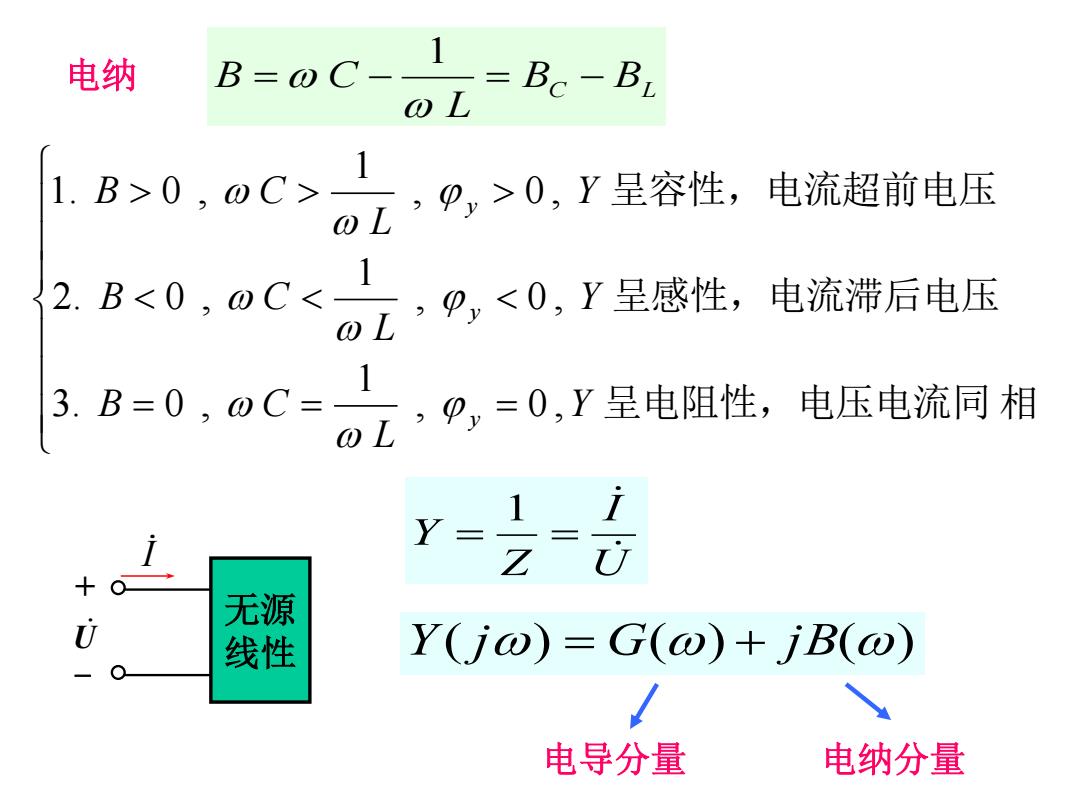
电纳 B-0C-0L- BC-B 3>0,oC>,>≥0，Y呈容性，电流超前 2.B<0,oC<,9,<0,Y呈感性，月 电流滞后电压 3B=0,0C=,0,=0,Y呈电阻性，电压电流同术 1 Y= Z U 无源 U 线性 Y(jω)=G(o)+jB(ω) 电导分量 电纳分量

                  呈电阻性，电压电流同 相 呈感性，电流滞后电压 呈容性，电流超前电压 , 0 , 1 3. 0 , , 0 , 1 2. 0 , , 0 , 1 1. 0 , Y L B C Y L B C Y L B C y y y          BC BL L B  C    1  电纳  无源 线性 I  U  + - U I Z Y     1 Y( j)  G()  j B() 电导分量 电纳分量

三、阻抗和导纳的关系 1 Y Z .Z(j)Y(jo)=1 Z(jw)Y(jω引=1， Pz+P=0 注意： N。含有受控源时，可有Re[Z(jo】90°情况

三、阻抗和导纳的关系 Z 1  Y  Z( j) Y( j) 1 ,  Z  y  0  Z( j)Y( j) 1 注意： N0 含有受控源时，可有 ReZ( j)  0，或  Z  900 情况