
重点内容 ◇电压电流参考方向,关联参考方向:基尔霍夫定律 (KCL,KVL) ◇基本元件伏安关系,功率(电阻,电容,电感) ◇理想电源:电压源和电流源的等效变换 ◇支路,节点,回路概念;电阻电路等效变换(串、并联) ◇支路电流发,节点电压法,:叠加定理,戴维南等效定理 ◇运算放大器电阻电路-虚断,虚短 ◇一阶电路时域分析一三要素法,时间常数 ◇ 正弦稳态电路分析-P,Q,S功率 ◇电阻,电感,电容一阻抗,导纳,电压电流相量关系,相位差 ◇最大功率计算 。 戴维南等效,节点电压法,KVL,KCL

◇理想变压器电路 ◇RLC串联电路-:谐振,品质因数Q ⊙并联谐振 ◇对称三相电源基本概念: ◇对称星型连接-线电压与相电压的关系 ◇二端口网络的z参数矩阵求解
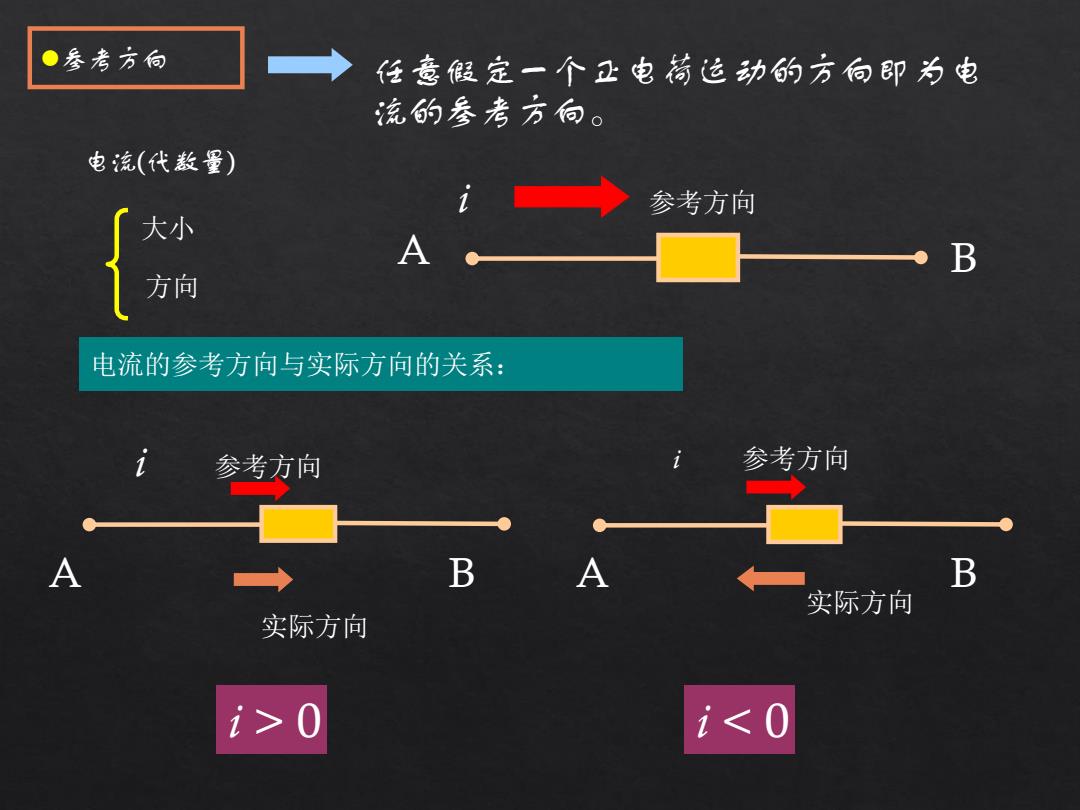
●叁老方向 任意假定一个正电荷运动的方向即为电 流的参老方向。 电流(代敖量) 参考方向 大小 A B 方向 电流的参考方向与实际方向的关系: 参考方向 参考方向 A B A B 实际方向 实际方向 i>0 i<0
参考方向 i 参考方向 大小 方向 电流(代数量) 任意假定一个正电荷运动的方向即为电 流的参考方向。 A B i 参考方向 i 参考方向 i > 0 i < 0 实际方向 实际方向 电流的参考方向与实际方向的关系: A B A B
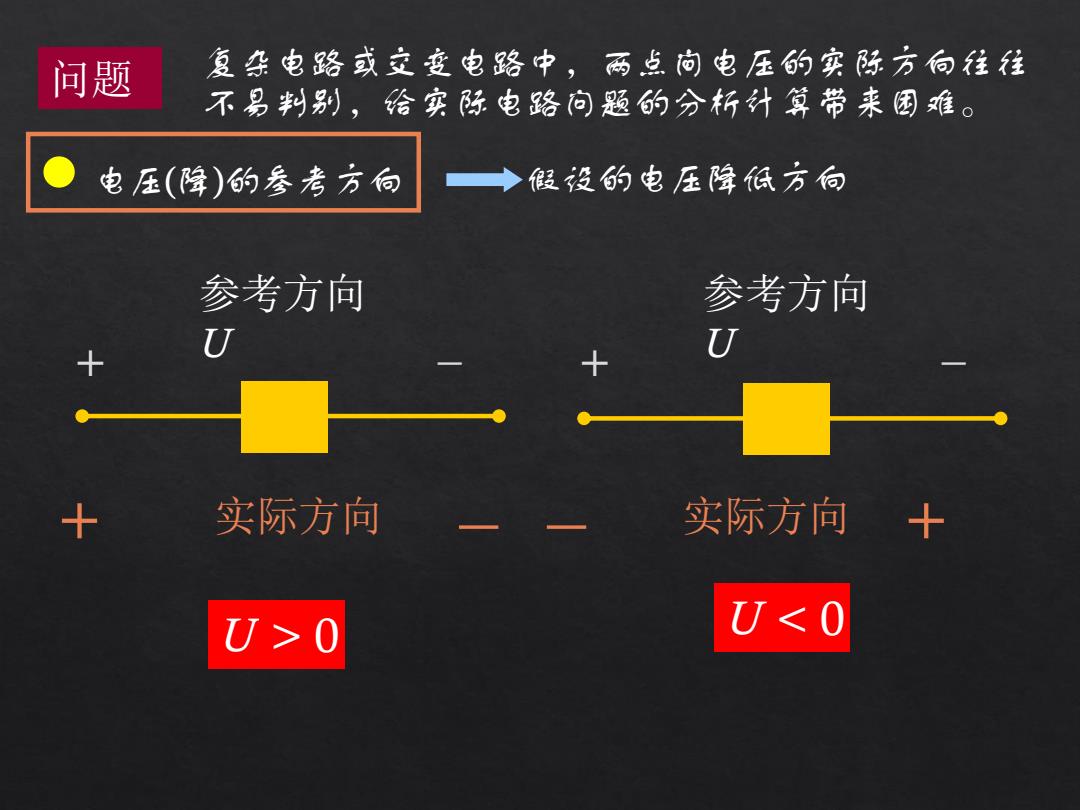
问题 复杂电路或立变电路中,两点向电压的实际方向往往 不易判别,给实际电路向题的分析计算带来困难。 电压(降)的参考方向 假设的电压降低方向 参考方向 参考方向 U U 实际方向 实际方向十 U>0 U<0
问题 复杂电路或交变电路中,两点间电压的实际方向往往 不易判别,给实际电路问题的分析计算带来困难。 电压(降)的参考方向 U 0 参考方向 U + – + 实际方向 实际方向 + 参考方向 U + – U 假设的电压降低方向
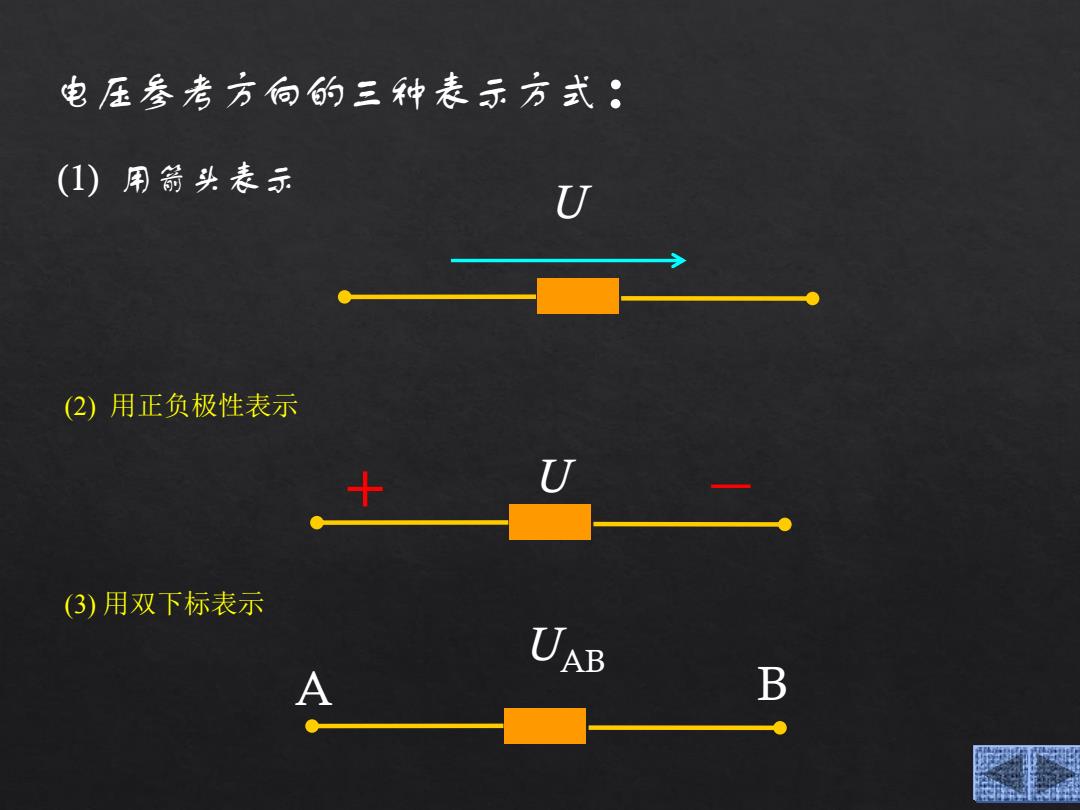
电压参考方向的三种表示方式: (1)用箭头表示 (2)用正负极性表示 (3)用双下标表示 UAB A B
电压参考方向的三种表示方式: (1) 用箭头表示 (2) 用正负极性表示 (3) 用双下标表示 U + U A B UAB
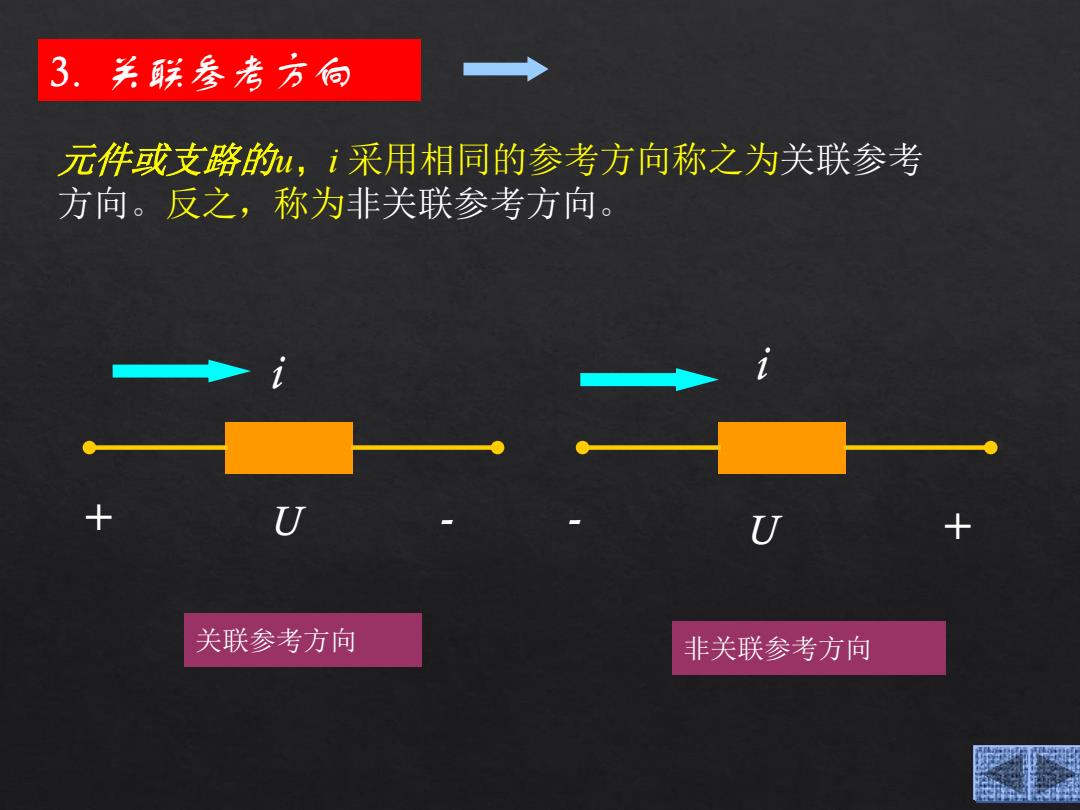
3.关联参老方向 元件或支路的,i采用相同的参考方向称之为关联参考 方向。反之,称为非关联参考方向。 关联参考方向 非关联参考方向
元件或支路的u,i 采用相同的参考方向称之为关联参考 方向。反之,称为非关联参考方向。 关联参考方向 非关联参考方向 3. 关联参考方向 i + - - + i U U
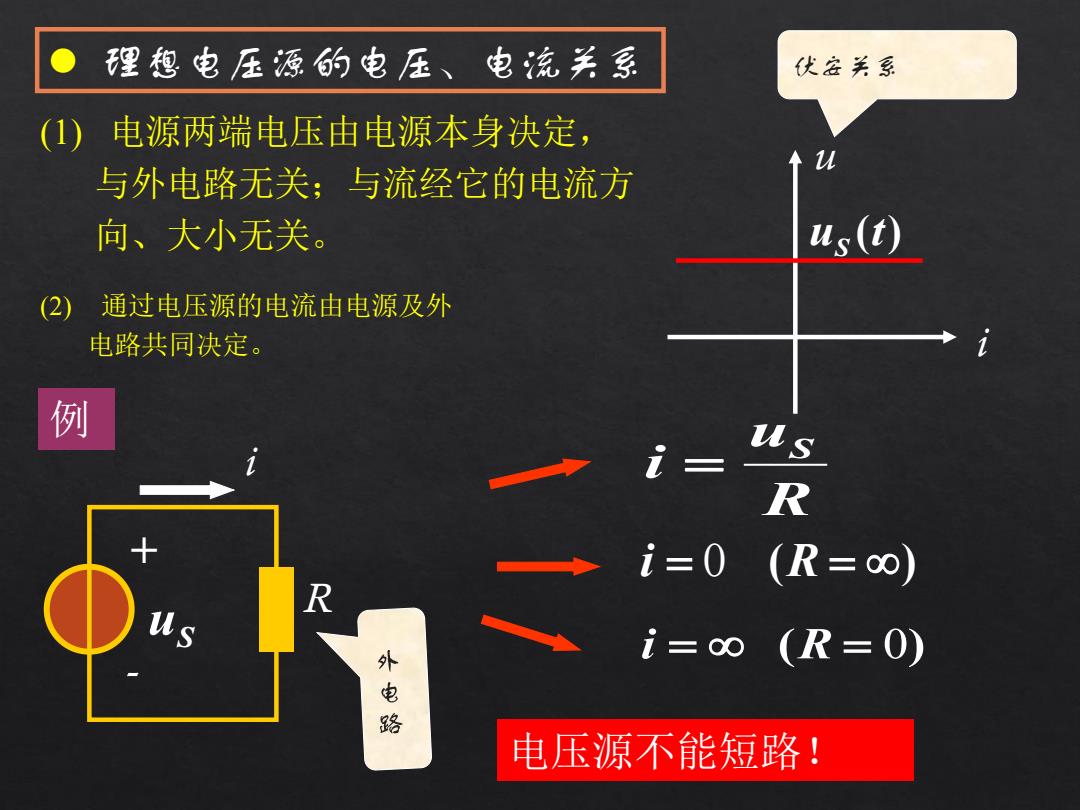
理想电压源的电压、电流关系 伏会关系 (1)电源两端电压由电源本身決定, 与外电路无关;与流经它的电流方 向、大小无关。 4s(t) (2) 通过电压源的电流由电源及外 电路共同决定。 例 i= s R i=0(R=∞) us i=∞(R=0) 外电路 电压源不能短路!
(1) 电源两端电压由电源本身决定, 与外电路无关;与流经它的电流方 向、大小无关。 (2) 通过电压源的电流由电源及外 电路共同决定。 理想电压源的电压、电流关系 u i u (t) S 伏安关系 例 R i - + uS R u i S i 0 (R ) i (R 0) 电压源不能短路!
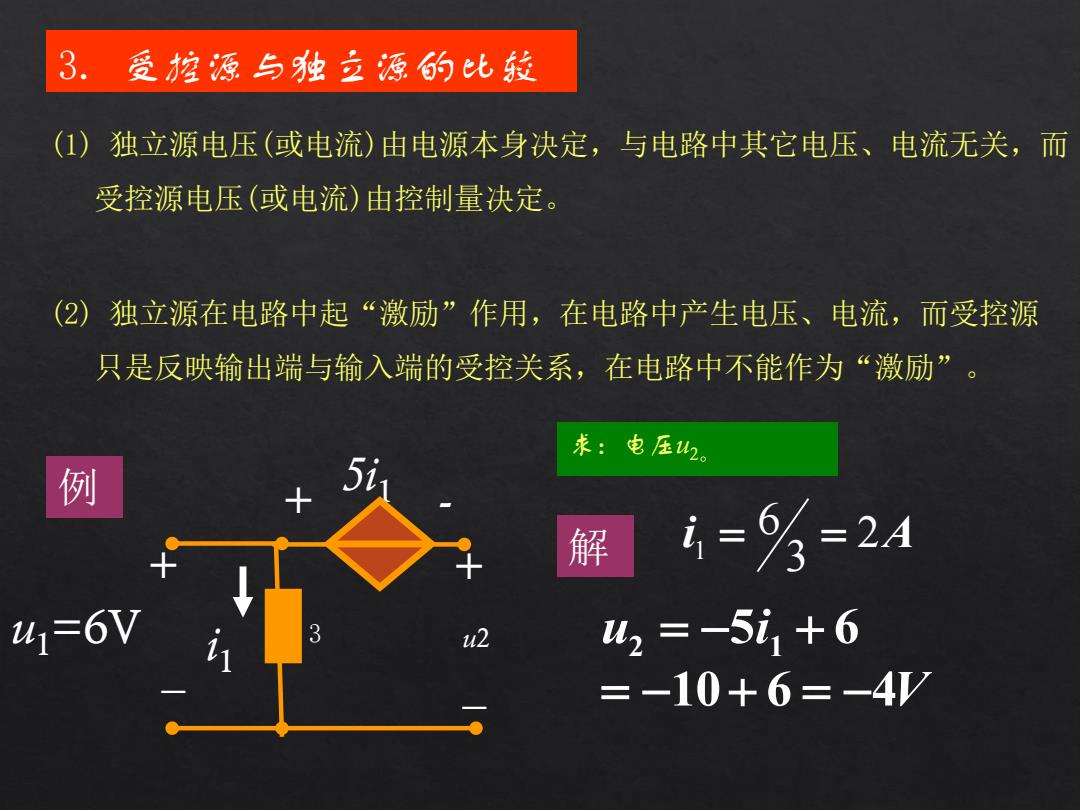
3.受控源与独立源的比粒 ()独立源电压(或电流)由电源本身决定,与电路中其它电压、电流无关,而 受控源电压(或电流)由控制量决定。 (2) 独立源在电路中起“激励”作用,在电路中产生电压、电流,而受控源 只是反映输出端与输入端的受控关系,在电路中不能作为“激励”。 求:电压42。 例 5i, 解 1=%=2A 41=6V 2 u2=-5i1+6 =-10+6=-4V
3. 受控源与独立源的比较 (1) 独立源电压(或电流)由电源本身决定,与电路中其它电压、电流无关,而 受控源电压(或电流)由控制量决定。 (2) 独立源在电路中起“激励”作用,在电路中产生电压、电流,而受控源 只是反映输出端与输入端的受控关系,在电路中不能作为“激励”。 例 求:电压u2。 解 5i1 + _ u2 _ u1=6V i1 + + - 3 i 2A 3 6 1 V u i 10 6 4 5 6 2 1

2.基尔霍夫电流定律 (KCL) 在集总参数电路中,任意时刘,对任意结点流出或流入孩结点电流的代数和等 于零。 流进的电流 ∑i(t)=0 等于流出的 or ∑i以=出 电流 k=1 例 今流出为“+”,有: -i1-i2+i3+i4+i5=0 i+2=i3+i4+i5
2. 基尔霍夫电流定律 (KCL) 例 令流出为“+”,有: 在集总参数电路中,任意时刻,对任意结点流出或流入该结点电流的代数和等 于零。 m k i t 1 ( ) 0 or i 入 =i 出 流进的电流 等于流出的 电流 1 i 5 i 4 i 3 i 2 i i 1 i 2 i 3 i 4 i 5 0 1 2 3 4 5 i i i i i
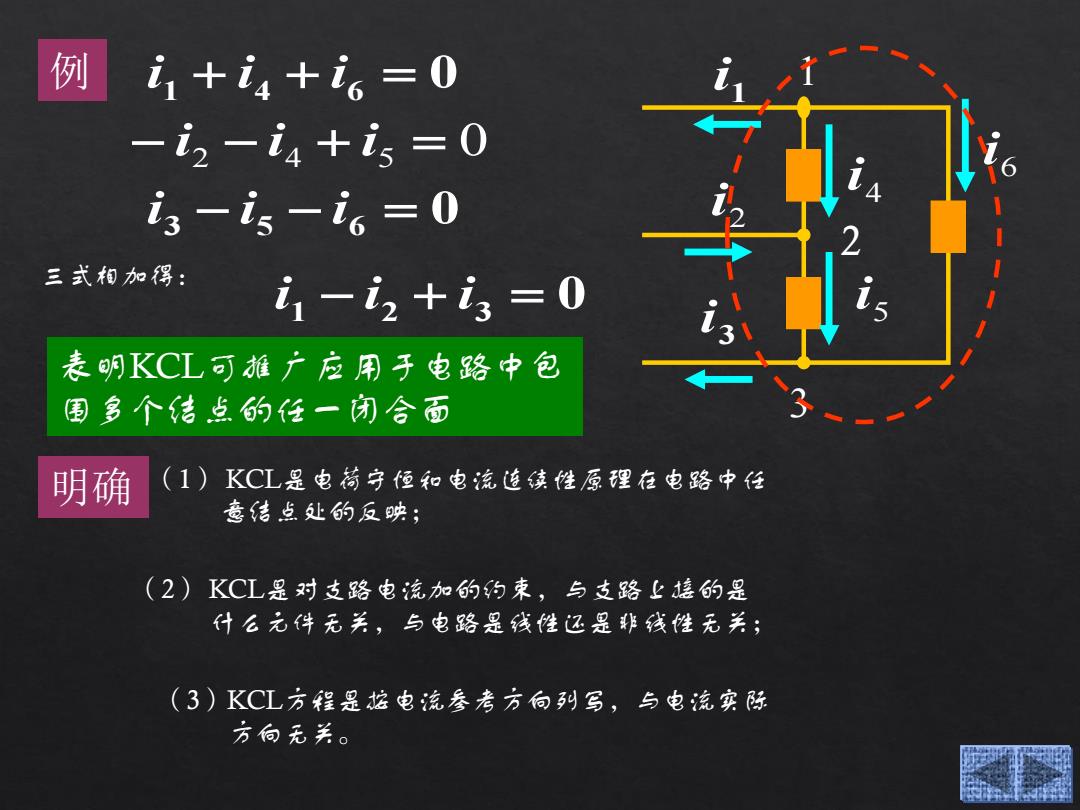
例 i1+i4+i6=0 -i2-i4+i5=0 i3-i5-i6=0 三式相加得: i1-i2+i3=0 表明KCL可推广应用于电路中包 围多个结点的任一闭合面 明确 (1)KCL是电荷守恒和电流连续性原理在电路中任 意结点处的反映; (2)KCL是对支路电流加的约束,与支路上接的是 什么元件无关,与电路是线性还是排线性无关; (3)KCL方程是炫电流参老方向列写,与电流实际 方向无关
1 3 2 5 i 6 i 4 i 1 i 3 i 2 i 例 i 1 i 4 i 6 0 i 2 i 4 i 5 0 i 3 i 5 i 6 0 三式相加得: i 1 i 2 i 3 0 表明KCL可推广应用于电路中包 围多个结点的任一闭合面 明确 (1) KCL是电荷守恒和电流连续性原理在电路中任 意结点处的反映; (2) KCL是对支路电流加的约束,与支路上接的是 什么元件无关,与电路是线性还是非线性无关; (3)KCL方程是按电流参考方向列写,与电流实际 方向无关