第七章 一阶电路的时域分析 主要内容: 1.动态电路的概念、方程及其初始条件 2.一阶电路的时间常数 三要素法 3.一阶电路的零输入响应零状态响应○全响应
主要内容: 1. 动态电路的概念、方程及其初始条件 2. 一阶电路的时间常数 3.一阶电路的零输入响应 零状态响应 全响应 第七章 一阶电路的时域分析 三要素法

§7-1 动态电路的方程及其初始条件 一、动态电路概述 1.1电阻电路与动态电路 电阻电路:电路中仅由电阻元件和电源元件构成。 KCL、KVL方程和元件特性均为代数方程。 因此描述电路的方程为代数方程。 (即时电路) 动态电路:含储能元件L(0、C。KCL、KVL方程仍 为代数方程,而元件方程中含微分或积分形 式。因此描述电路的方程为微分方程。 (记忆电路)
一、动态电路概述 §71 动态电路的方程及其初始条件 1.1 电阻电路与动态电路 动态电路:含储能元件L(M)、C。KCL、KVL方程仍 为代数方程,而元件方程中含微分或积分形 式。因此描述电路的方程为微分方程。 (记忆电路) 电阻电路:电路中仅由电阻元件和电源元件构成。 KCL、KVL方程和元件特性均为代数方程。 因此描述电路的方程为代数方程。 (即时电路)
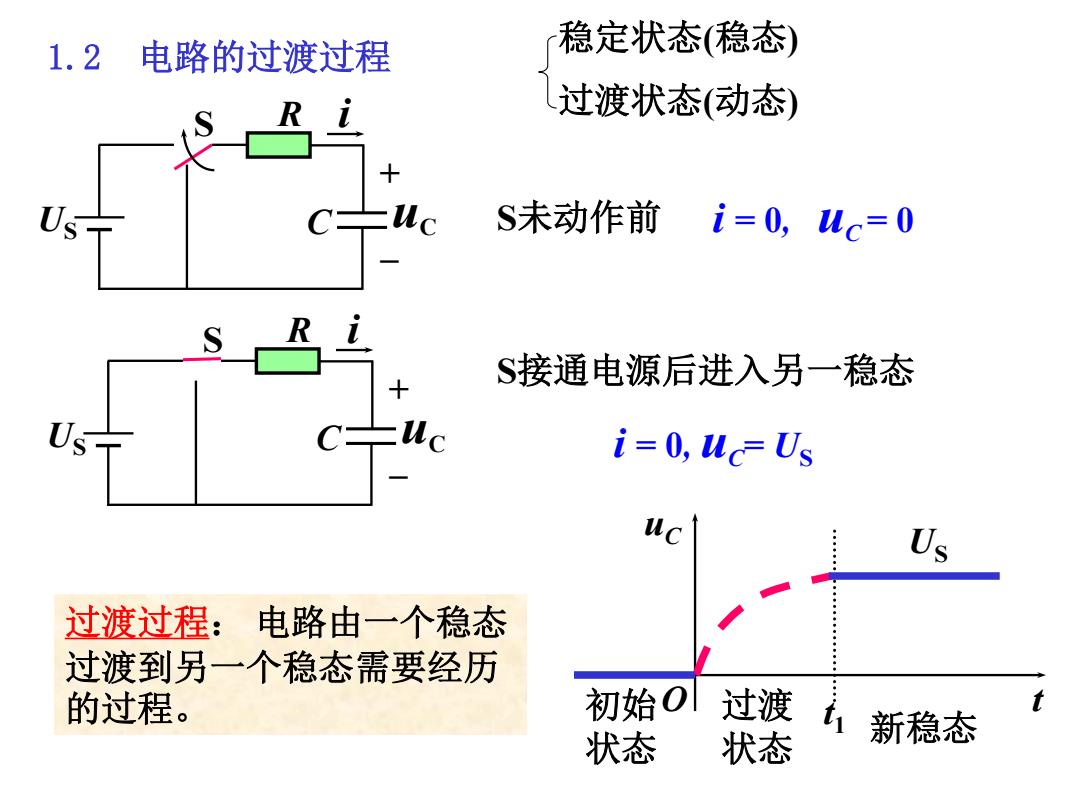
1.2 电路的过渡过程 稳定状态稳态) 过渡状态动态) S未动作前 i=0,Wc=0 R S接通电源后进入另一稳态 i=0,Uc=Us uc U 过渡过程:电路由一个稳态 过渡到另一个稳态需要经历 的过程。 初始O过渡 状态 状态 新稳态
1.2 电路的过渡过程 S未动作前 S接通电源后进入另一稳态 i = 0, uC = 0 i = 0, uC= US S + – US uC R C i S + – US uC R C i 过渡过程: 电路由一个稳态 过渡到另一个稳态需要经历 的过程。 稳定状态(稳态) 过渡状态(动态) uC t t1 US 初始O 状态 过渡 状态 新稳态
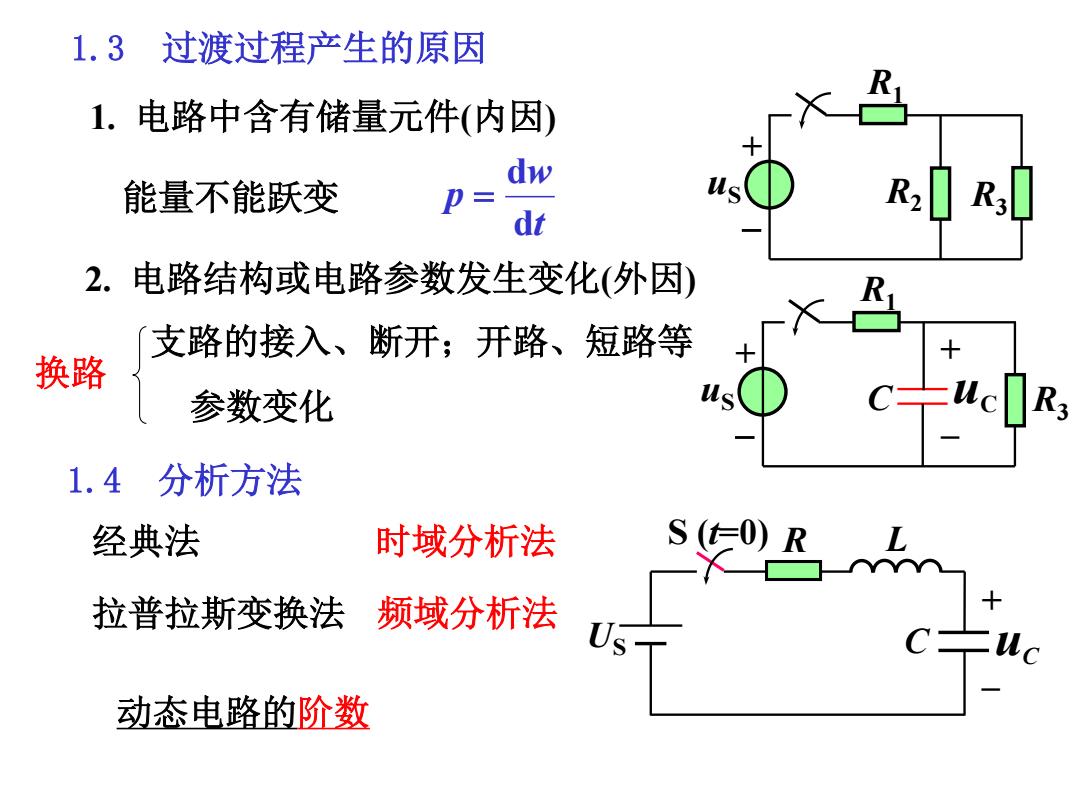
1.3过渡过程产生的原因 1.电路中含有储量元件(内因) dw 能量不能跃变 p= dt 2.电路结构或电路参数发生变化(外因) R 支路的接入、断开;开路、短路等 换路 参数变化 s 1.4分析方法 经典法 时域分析法 拉普拉斯变换法 频域分析法 UsT 动态电路的阶数
1.3 过渡过程产生的原因 1. 电路中含有储量元件(内因) 能量不能跃变 t w p d d 2. 电路结构或电路参数发生变化(外因) 支路的接入、断开;开路、短路等 + uS R1 R2 R3 参数变化 换路 + – C uC + uS R1 R3 1.4 分析方法 经典法 时域分析法 拉普拉斯变换法 频域分析法 S (t=0) L US C + – uC R 动态电路的阶数
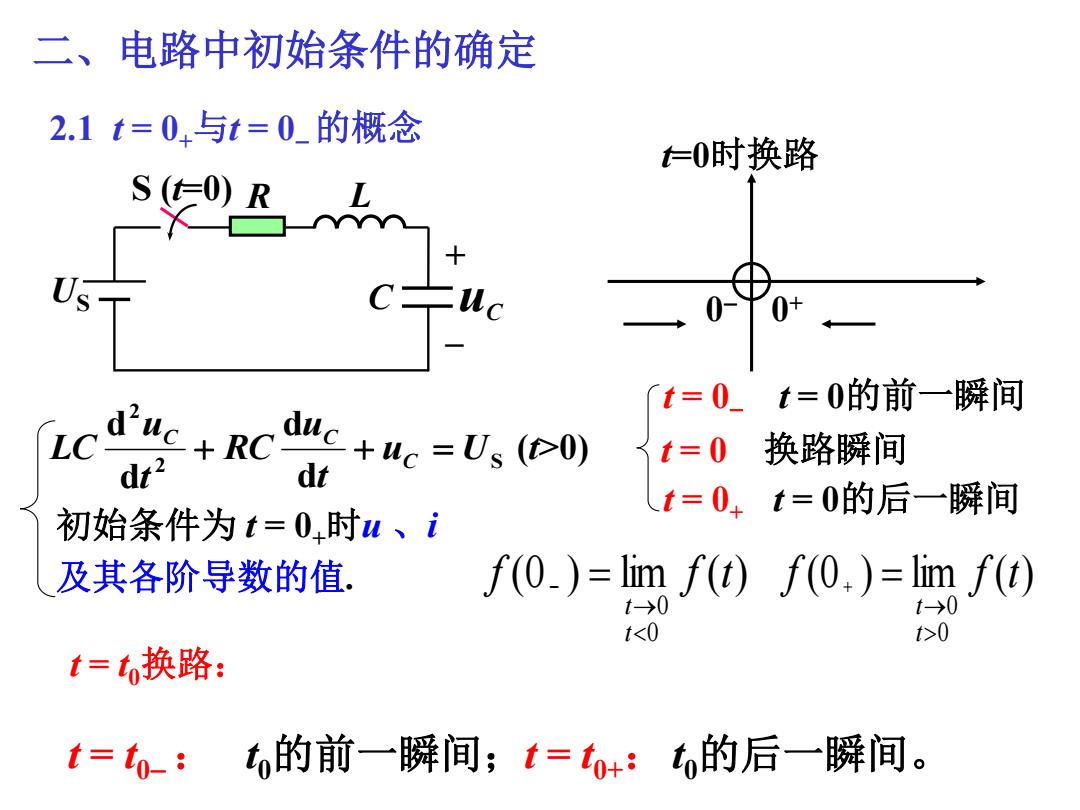
二、电路中初始条件的确定 2.1t=0,与t=0的概念 t=O时换路 0+ 「t=0_t=0的前一瞬间 LC+RC dc+e=Us ( 3t=0 换路瞬间 dt? dt t=0+t=0的后一瞬间 初始条件为t=0,时u、i 及其各阶导数的值, f(0)=lim f(1)f(0.)=lim f(t) t→0 t→0 t0 t=t换路: t=tn:的前一瞬间;t=t+:t的后一瞬间
二、电路中初始条件的确定 2.1 t = 0+与t = 0的概念 t=0时换路 t = 0 t = 0的前一瞬间 t = 0+ t = 0的后一瞬间 2 S t = 0 换路瞬间 2 d d d d u U t u RC t u LC C C C 0 0 + (0 ) lim ( ) 0 0 f f t t t (0 ) lim ( ) 0 0 f f t t t t = t0: t0的前一瞬间;t = t0+: t0的后一瞬间。 初始条件为 t = 0+时u 、i 及其各阶导数的值. S (t=0) L US C + – uC R (t>0) t = t0换路:

2.2换路定则(开闭定则) A电容的电荷和电压 十 9c()=i(5)d5 k.)=3 uc 宁C-55+ga5「5+2〔ea dq dt =9c(0.)+i(5)d5 F40)+255 4c=Cuc qc(0.)=9c0.)+0i(5)d5 当t=0时, 0,)=40)+25a 当)为有限值时, 05d5=0 9c(0+)=9c(0) Lc(0+)=uc(0)
2.2 换路定则 (开闭定则) 当t = 0+时, ()d 1 (0 ) (0 ) 0 0 i C u u C C C i uC + – (0 ) ( )d ( )d ( )d ( ) ( )d 0 0 0 t C t t C q i i i q t i ( )d 1 (0 ) ( )d 1 ( )d 1 ( )d 1 ( ) 0 0 0 t C t t C i C u i C i C i C u t (0 ) (0 ) ()d 0 0 q q i C C ( )d 0 0 0 i qC (0+ ) = qC (0 ) uC (0+ ) = uC (0 ) 当i(t)为有限值时, t q i d d qC =CuC A 电容的电荷和电压

B电感的磁链和电流 平,)=广45d5 3=5u5+「g5 0=八5 F2L5N+汇M55 u= dΨ =平,0.)+5d5 dt 0)+dg 平L 当t=0,时, Ψ,(0.)=Ψ,(0.)+a5)d5 0.)-i0.+2C405 当40为有限值时,4(5d上=0g0,)=光(0) iz(04)=iz(0)
B 电感的磁链和电流 当t = 0+时, ()d 1 (0 ) (0 ) 0 0 u L i i L L (0 ) ( )d ( )d ( )d ( ) ( )d 0 0 0 t L t t L u u u t u ( )d 1 (0 ) ( )d 1 ( )d 1 ( )d 1 ( ) 0 0 0 t L t t L u L i u L u L u L i t (0 ) (0 ) ( )d 0 0 u L L ( )d 0 0 0 u L (0+ ) = L (0 ) iL (0+ ) = iL (0 ) 当u(t)为有限值时, t u L d d L =LiL L iL u + –

小结: ()一般情况下电容电流、电感电压均为有限值,换路定则成立。 9c(0+)=Ic(0) '(0+)=必(0-) 换路定则: Wc(0)=uc(0_) i(0)=i0) (2)换路定则是建立在能量不能突变的基础上. 2.3电路初始条件的确定 独立初始条件 uc(0.) i(0,) 非独立初始条件 电阻电压或电流、电容电流、电感电压
小结: (2) 换路定则是建立在能量不能突变的基础上. (1) 一般情况下电容电流、电感电压均为有限值,换路定则成立。 L (0+ )= L (0 ) iL (0+ )= iL (0 ) qC (0+ ) = qC (0 ) uC (0+ ) = uC (0 ) 换路定则: 2 2 1 WC CuC 2 2 1 WL LiL 2.3 电路初始条件的确定 (0 ) C u (0 ) L i 非独立初始条件 独立初始条件 电阻电压或电流、电容电流、电感电压

求初始值的一般方法: (1)由换路前电路求u.(0)和iz(0): (2)由换路定则,得uc0+)和i(0+): 3)作0等效电路: 电容用电压为u0+)的电压源替代; 电感用电流为,(0+)的电流源替代。 (4)由0+电路求所需的u(0+)、0+),即非独立初始条件
求初始值的一般方法: (1) 由换路前电路求uc (0 )和iL (0 ); (2) 由换路定则,得uC (0+ )和iL (0+ ); (3) 作0+等效电路: (4) 由0 +电路求所需的u(0+ )、i(0+ ) ,即非独立初始条件。 电容用电压为uC (0+ )的电压源替代; 电感用电流为iL (0+ )的电流源替代
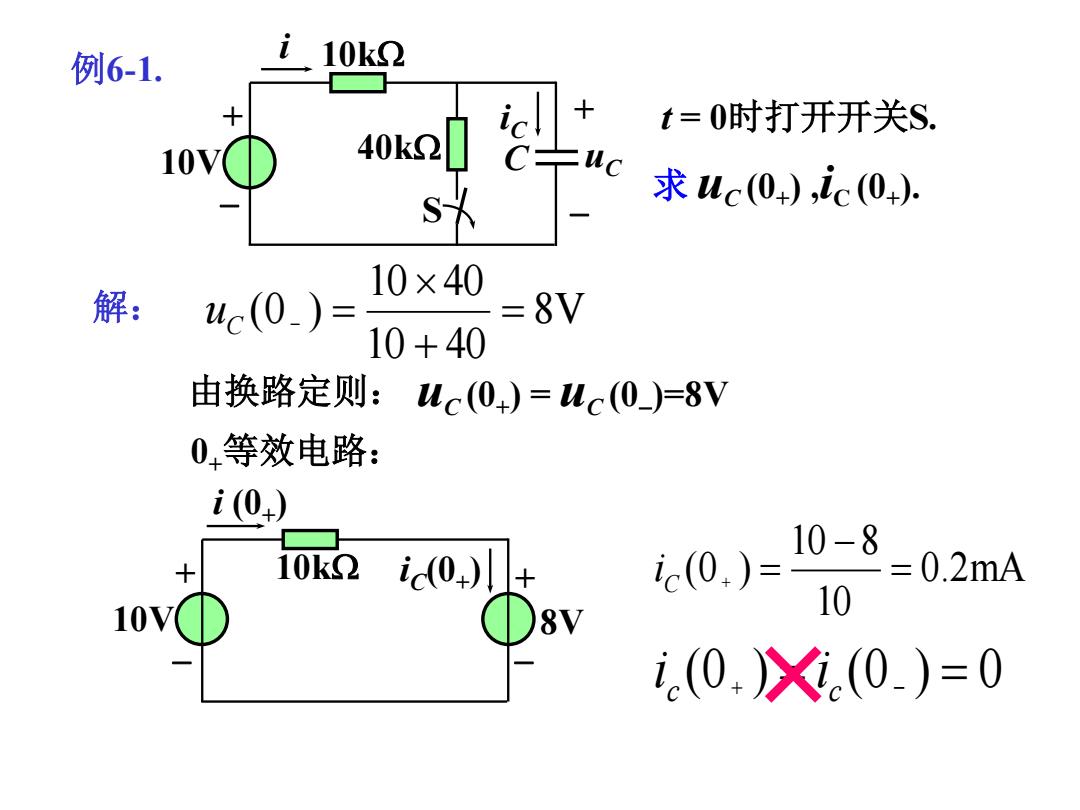
例6-1. i. 10k2 十 t=0时打开开关S. 10V( uc s 求uc0),ic(0+ 10×40 解:uc(0)= = 8V 10+40 由换路定则:uc(0+)=uc(0)=8V 0等效电路: i(0) 10- 10k2 i0++ c(0,)= 8=0.2mA 10V 1 8V i(0,X(0)=0
例6-1. 求 uC (0+ ) ,iC (0+ ). t = 0时打开开关S. 由换路定则: uC (0+ ) = uC (0 )=8V 8V 10 40 10 40 (0 ) uC 0+等效电路: 0.2mA 10 10 8 (0 ) i C (0 ) (0 ) 0 c c i i + 10V i iC uC S 10k 40k + C 解: + 10V i (0+ ) iC (0+ ) 8V 10k +