电阻电路习题课 (三) 32 1.求电流I。 U. 62 45V 42 6.42 15A 22 解:用戴维南定理: 42 32 o a + a 62 R 45V 42 15A 22 U 0 b 42
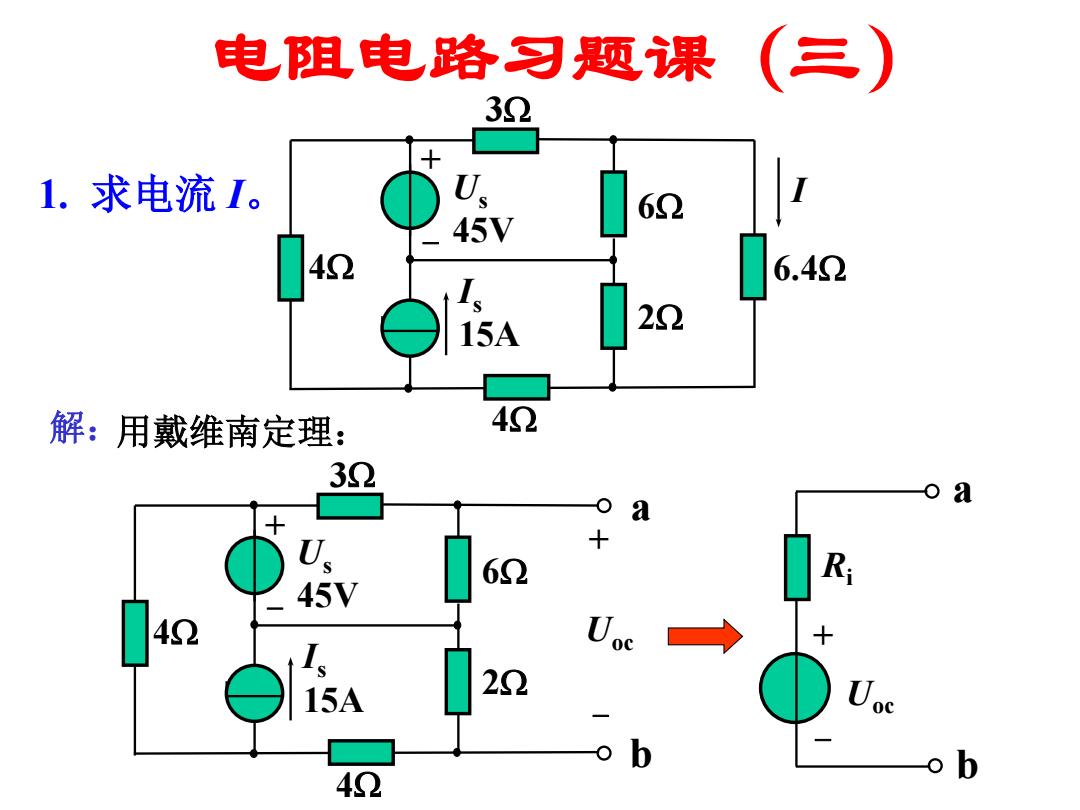
电阻电路习题课(三) 1. 求电流 I。 用戴维南定理: Us 45V Is 15A 3 4 6 2 4 6.4 I + - a b Uoc Us 45V Is 15A 3 4 6 2 4 + - + - 解: a b Uoc Ri + -
求开路电压U: 39 十十 a U. 62U1' 45V 42 Uoe' Uo'=U1'+U2 22U2' =30-9=21V b 42 32 a Uo"=U1"+U" + 62U1" =0+12=12V 42 15A 22U2" Uc=Uc'+Ue” =21+12=33V 42
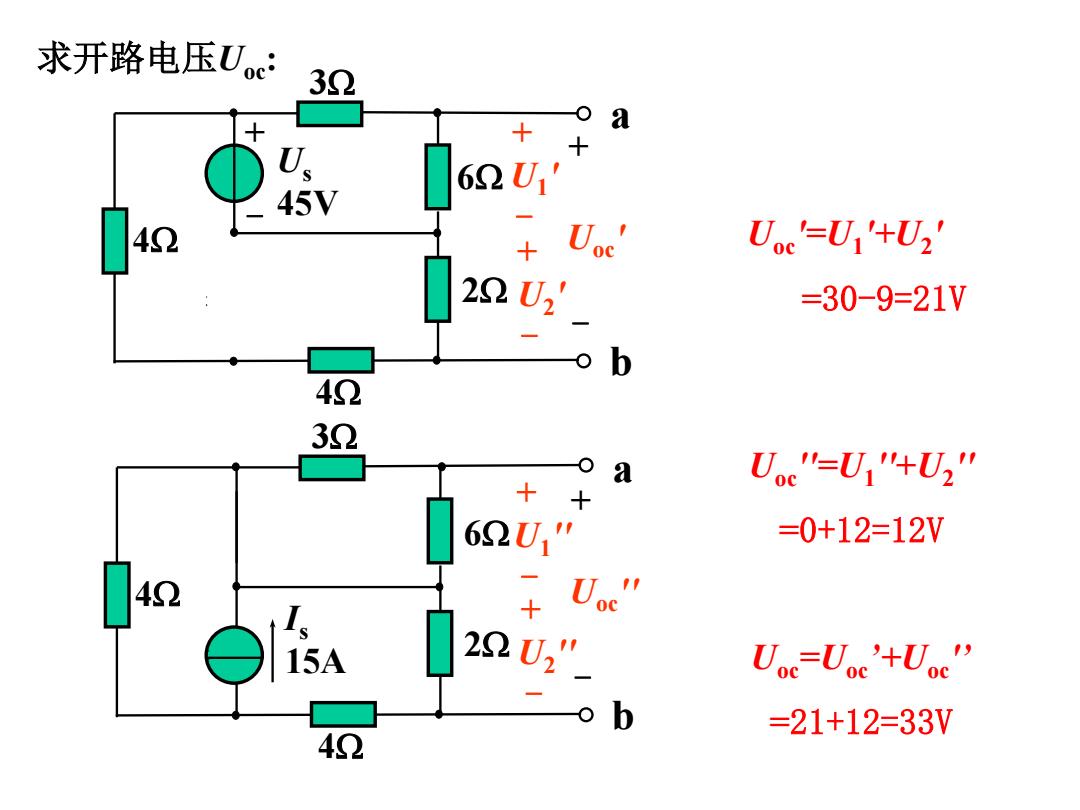
Uoc'=U1 '+U2 ' =30 -9=21V Uoc''=U1 ''+ U2 '' =0+12=12V Uoc=Uoc’+Uoc '’ =21+12=33V 求开路电压 Uoc : ab Uoc ' Us 45V3 4 6 2 4 +- +- +-U1 ' +-U2 ' ab Uoc '' Is 15A3 4 6 2 4 +- +-U1 '' +-U2
求内阻R: 32 a 62 + 42 U 20 b 42 a R 6.42 R=2+1.6=3.62 =33/(3.6+6.4)=3.3A 93 b
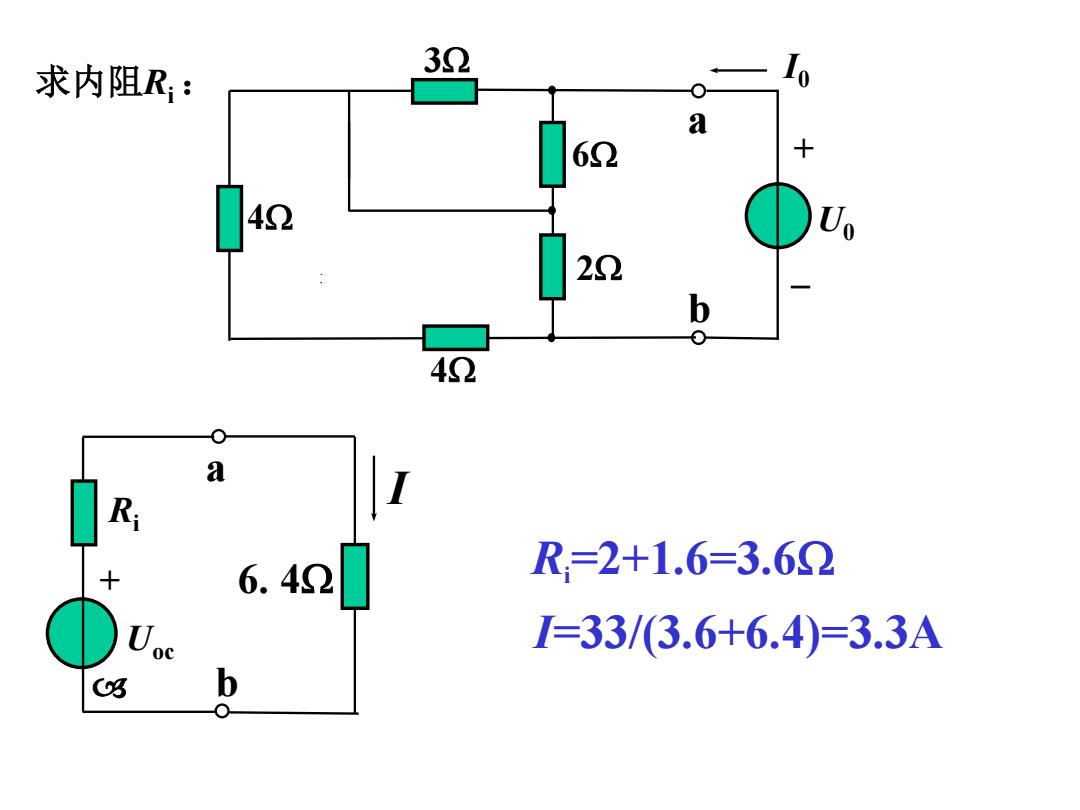
求内阻Ri : Ri =2+1.6=3.6 I=33/(3.6+6.4)=3.3A a b I0 U0 3 4 6 2 4 + 6. 4 I a b Uoc Ri +
2.用戴维南定理求I。 5U1 42 62 632 82 1A 62 -12V U 20 a 5U1 42 62 632 1A 62 12V bo U 20
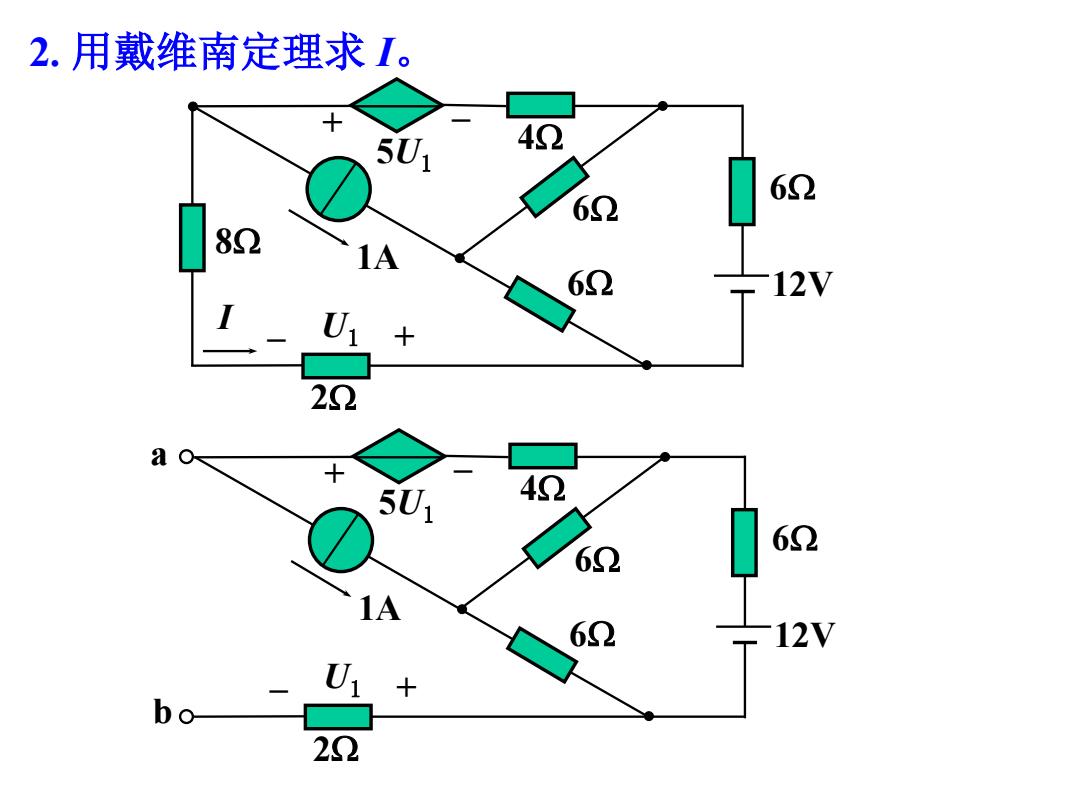
2. 用戴维南定理求 I 。 I8 2 4 6 6 6 5 U1 1 A 12 V + – – U1 + ab 2 4 6 6 6 5 U1 1 A 12 V + – – U1 +
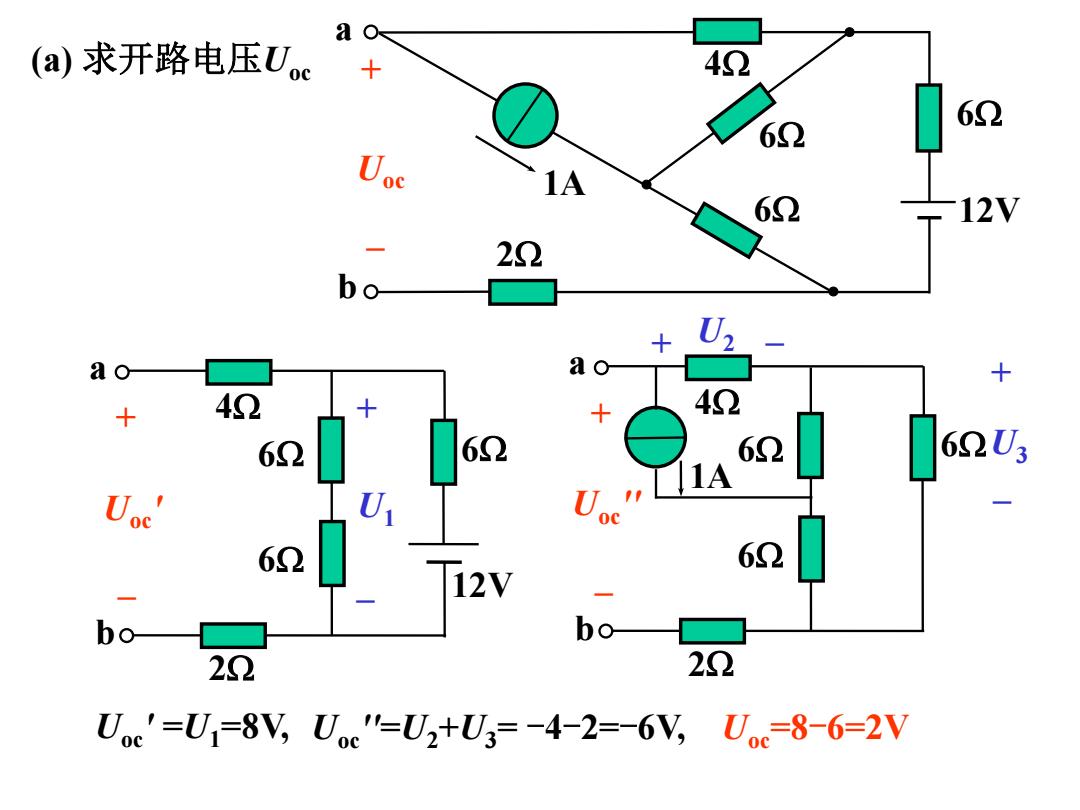
(a)求开路电压Uc 62 1A 62 12V b。 22 U ao + 42 42 62 62 62 62U3 1A U U 62 62 12V b。 b0 22 22 Uc'=U=8V,Ue"=U2+U3=-4-2=-6V,U=8-6=2V
Uoc' =U1=8V, Uoc ''=U2+U3= -4-2=-6V, Uoc=8-6=2V a b 2 4 6 6 6 1A 12V + – Uoc 2 4 6 6 6 12V b a + Uoc ' – + U1 – 1A 2 4 6 6 6 b a + Uoc '' – + U2 – + U3 – (a) 求开路电压Uoc
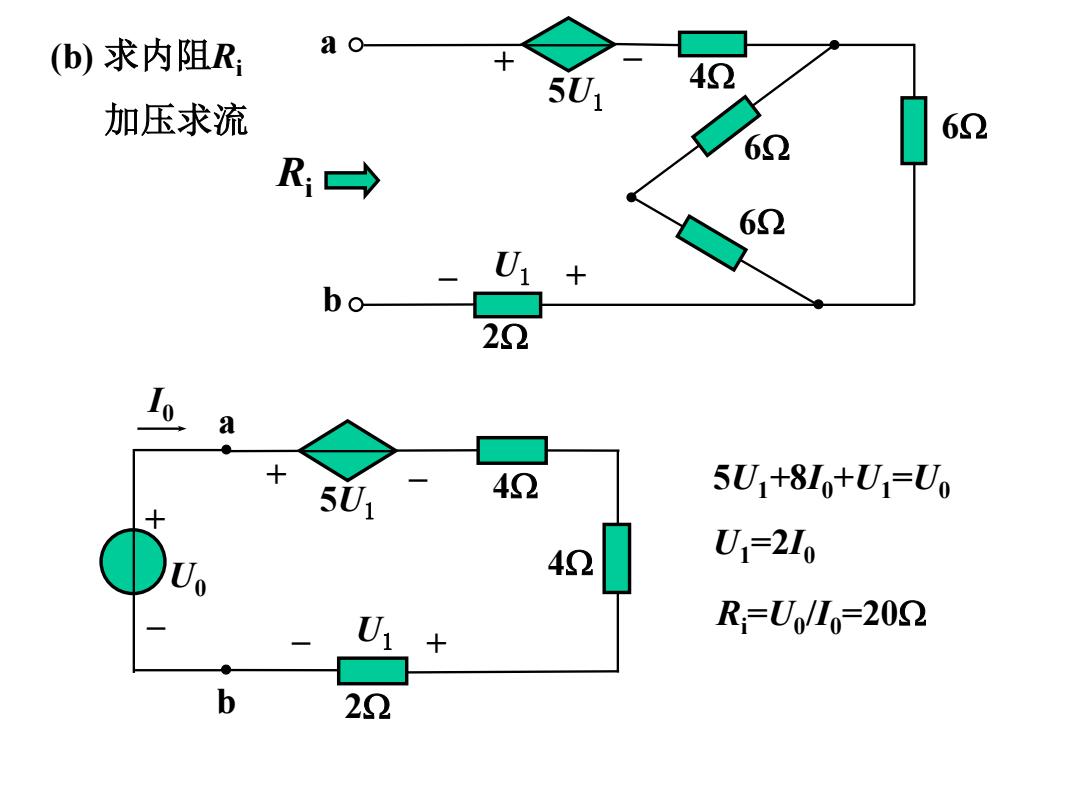
(b)求内阻R a o- 5U1 52 加压求流 62 R→ b0— U1+ 22 a 5U1 42 5Uj+810+U=Uo 42 U=210 U1+ R=U/I0=202 b 22
Ri (b) 求内阻Ri 加压求流 5U1+8I0+U1 =U0 U1=2I0 Ri =U0 /I0=20 a b 2 4 6 6 6 5U1 + – – U1 + 2 4 4 5U1 a b U0 I0 + – – U1 + + –
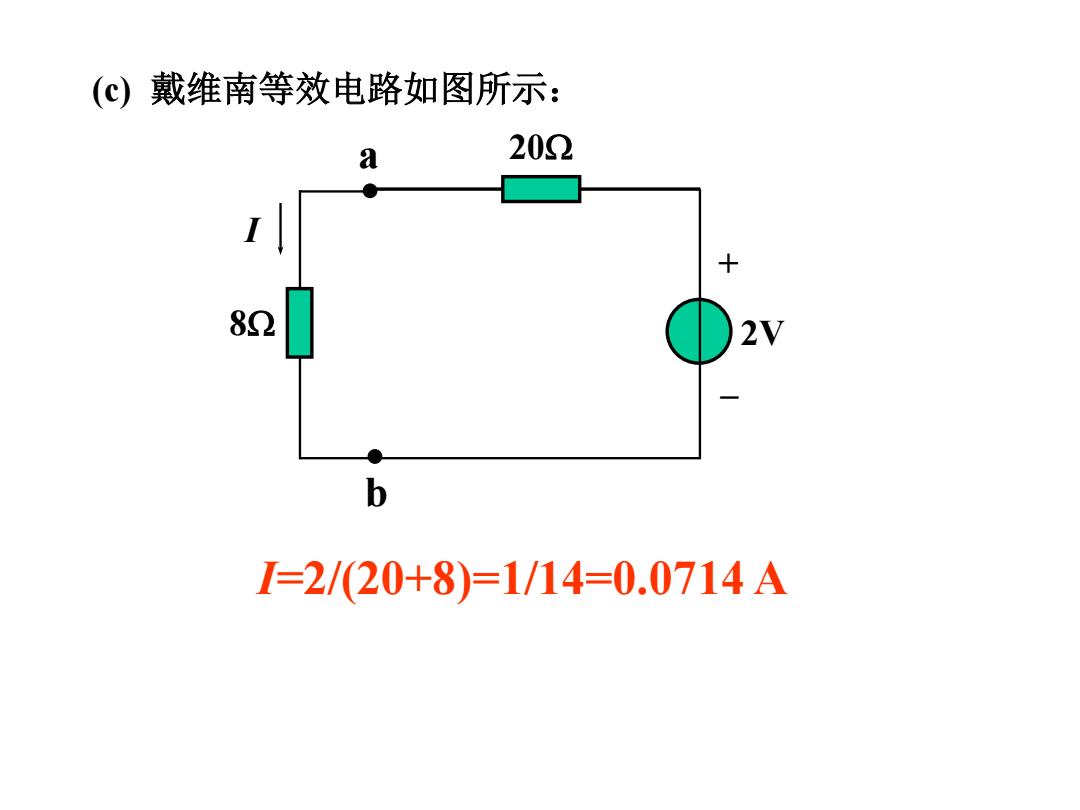
(c)戴维南等效电路如图所示: a 202 + 82 2V b I=2/(20+8)=1/14=0.0714A
(c) 戴维南等效电路如图所示: I=2/(20+8)=1/14=0.0714 A a b 20 8 2V I + –
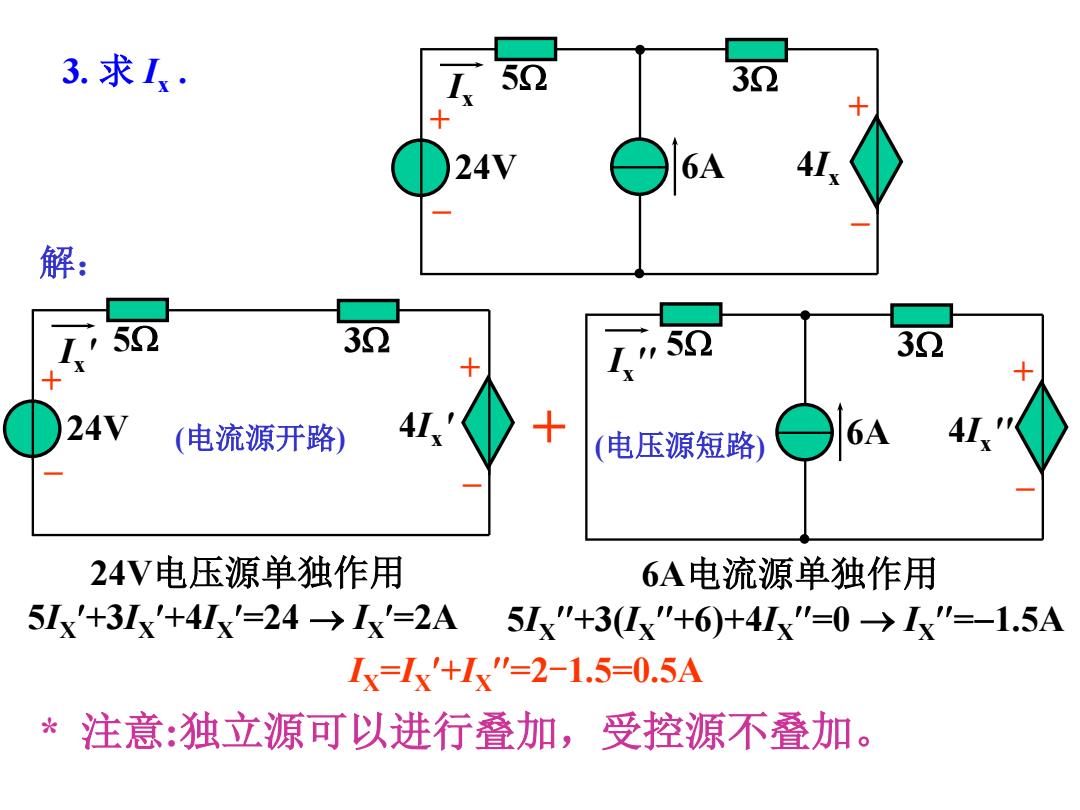
3.求1· 30 24V 解: ,52 32 24V (电流源开路) 十 (电压源短路) 6A 24V电压源单独作用 6A电流源单独作用 5Ix'+3Ix'+4Ix'=24>Ix'=2A 5Ix"+3(Ix"+6)+4Ix"=0→Ix"=-1.5A Ix-Ix'+1x"=2-1.5=0.5A *注意:独立源可以进行叠加,受控源不叠加
3. 求 Ix . 24V 6A I 5 3 x 4Ix + – + – 24V I 5 3 x ' 4Ix ' + – + – 解: 6A 5 3 Ix '' 4Ix '' + – + 24V电压源单独作用 6A电流源单独作用 5IX +3IX +4IX =24 IX =2A 5IX +3(IX +6)+4IX =0 IX =1.5A IX =IX +IX =2-1.5=0.5A * 注意:独立源可以进行叠加,受控源不叠加。 (电流源开路) (电压源短路)
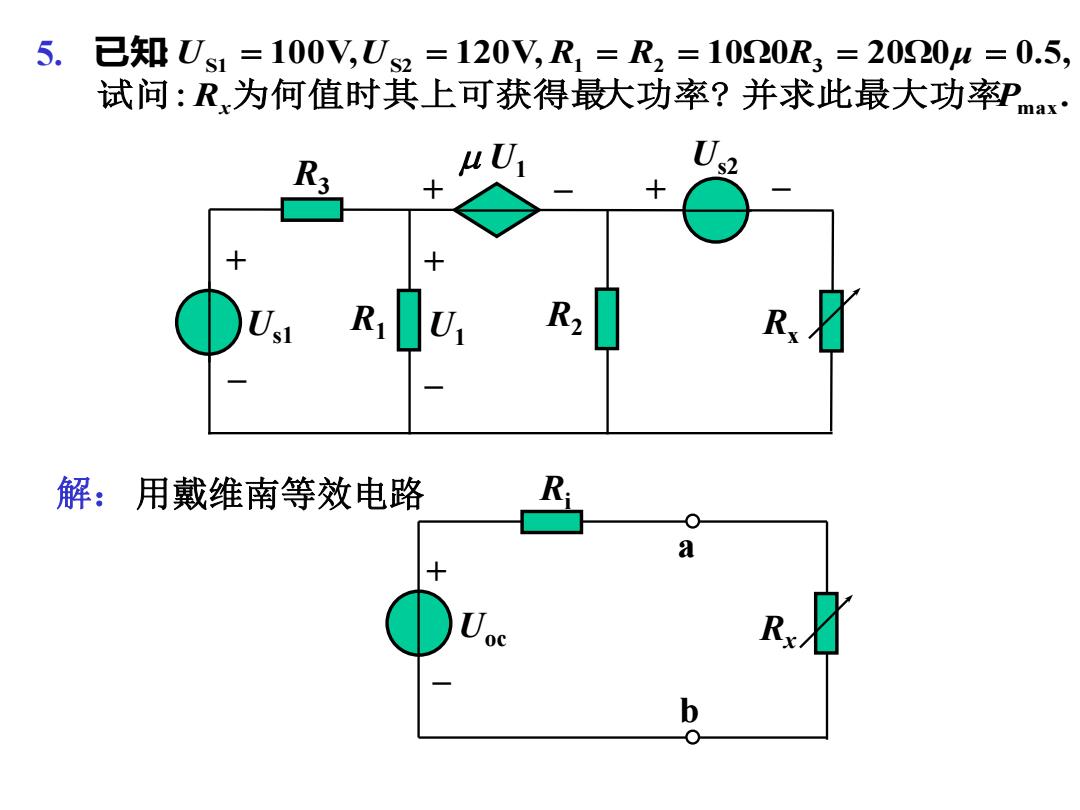
5.i 已知Us1=100V,Us2=120V,R1=R2=1020R3=2020u=0.5, 试问:R为何值时其上可获得最大功率?并求此最大功率?max R 1 解:用戴维南等效电路 a b 0
. 已 知 : 100V, 120V, 10Ω0 20Ω0 0.5, max S1 S2 1 2 3 R P U U R R R μ 试问: x为何值时其上可获得最大功率? 并求此最大功率 5. Rx 解: 用戴维南等效电路 Us1 R3 U1 U1 R1 R2 Us2 Rx + – + – + – + – Ri Uoc a b + –
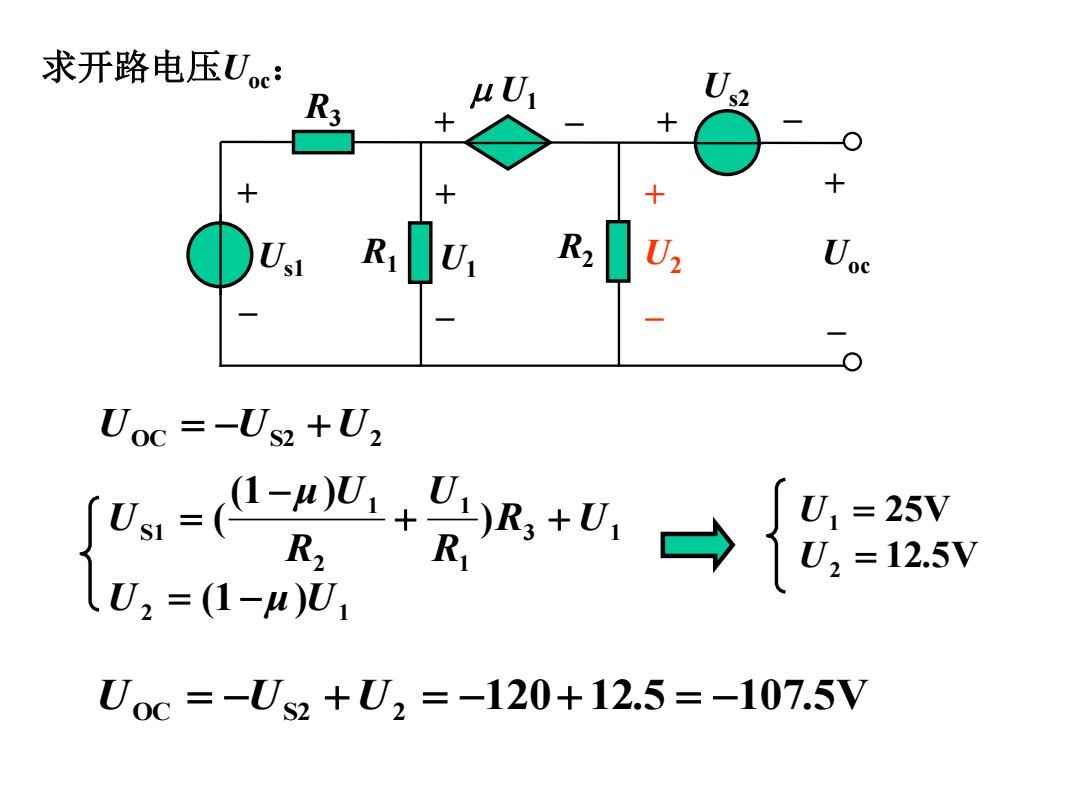
求开路电压Uc: R3 4U1 十 U2 -0 Uoc =-Us2 +U2 受风→{ R R 2=(1-n)U1 Uoc=-Us2+U2=-120+12.5=-107.5V
UOC US2 U2 2 1 3 1 1 1 2 1 S1 (1 ) ) (1 ) ( U μ U R U R U R μ U U 12.5V 25V 2 1 U U UOC US2 U2 120 12.5 107.5V 求开路电压Uoc: Us1 R3 U1 U1 R1 R2 Us2 + – + – + – + – + – U2 Uoc + –