
第三章 电阻电路的一般分析 主要内容: 1.图论的初步概念 2.支路电流法 3.网孔电流法和回路电流法 4.结点电压法
第三章 电阻电路的一般分析 主要内容: 1. 图论的初步概念 2. 支路电流法 3. 网孔电流法和回路电流法 4. 结点电压法

目的:找出一般(对任何线性电路均适用)的求解线性网络的 系统方法(易于计算机编程序求解)。 对象:含独立源、受控源的电阻网络的直流稳态解。 应用:主要用于复杂的线性电路的求解。 基础: 元件特性(VCR) 电路性质 对电阻,即U=R) 相互独立 拓扑约束一KCL,KVL
目的:找出一般(对任何线性电路均适用)的求解线性网络的 系统方法(易于计算机编程序求解) 。 对象:含独立源、受控源的电阻网络的直流稳态解。 应用:主要用于复杂的线性电路的求解。 电路性质 元件特性(VCR) (对电阻,即U=IR) 拓扑约束—KCL,KVL 相互独立 基础:

§3-1 电路的图 一、图 图G=(V,E):结点和支路的一个集合 结点(顶点,点):支路的汇合处 支路(线段,边):是一个抽象的线段(代表一个电路元件) 孤立结点: 不关联任何边的点 移去支路: 移去该支路,但其所关联的两个结点保持不变 移去结点: 把它所关联的全部支路同时移去
§31 电路的图 一、图 支路(线段,边):是一个抽象的线段(代表一个电路元件) 孤立结点: 移去结点: 移去该支路,但其所关联的两个结点保持不变 图 G = (V, E ): 结点和支路的一个集合 结点(顶点,点):支路的汇合处 不关联任何边的点 移去支路: 把它所关联的全部支路同时移去
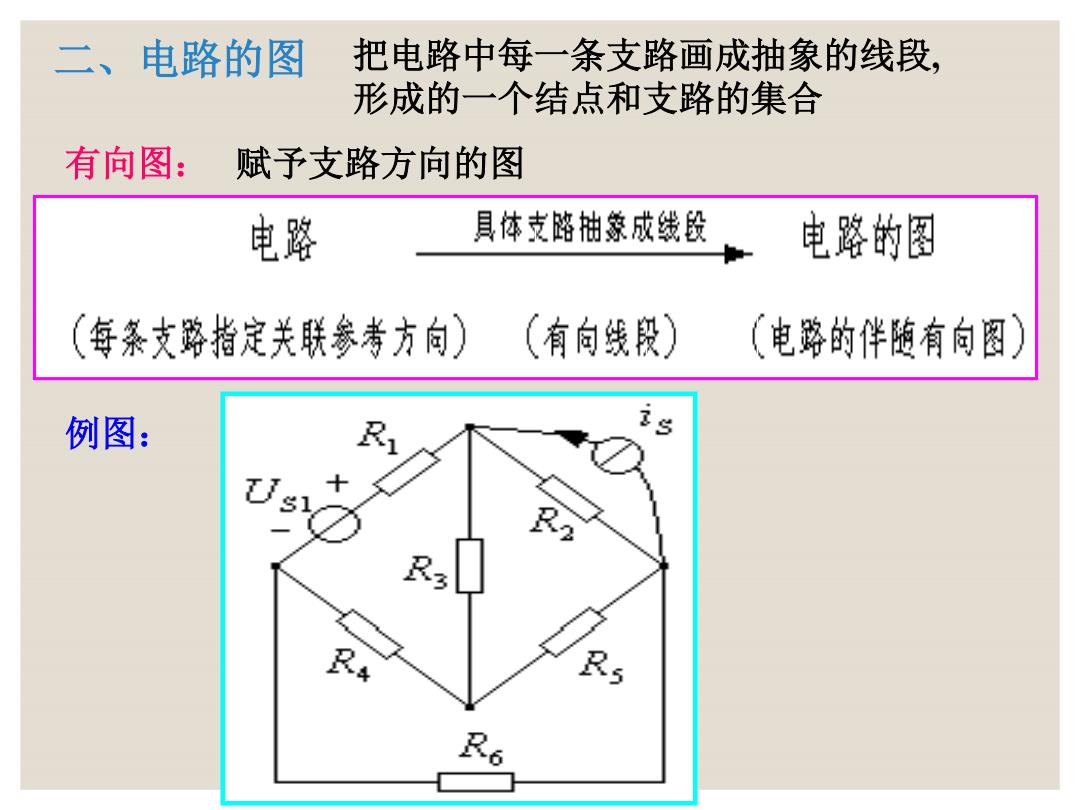
二、电路的图 把电路中每一条支路画成抽象的线段, 形成的一个结点和支路的集合 有向图:赋予支路方向的图 电路 具体支略抽象成线设 电路的图 (每案支路指定关联参考方向) (有向线段) (电路的伴随有向图 例图: R:
二、电路的图 把电路中每一条支路画成抽象的线段, 形成的一个结点和支路的集合 有向图: 赋予支路方向的图 例图:
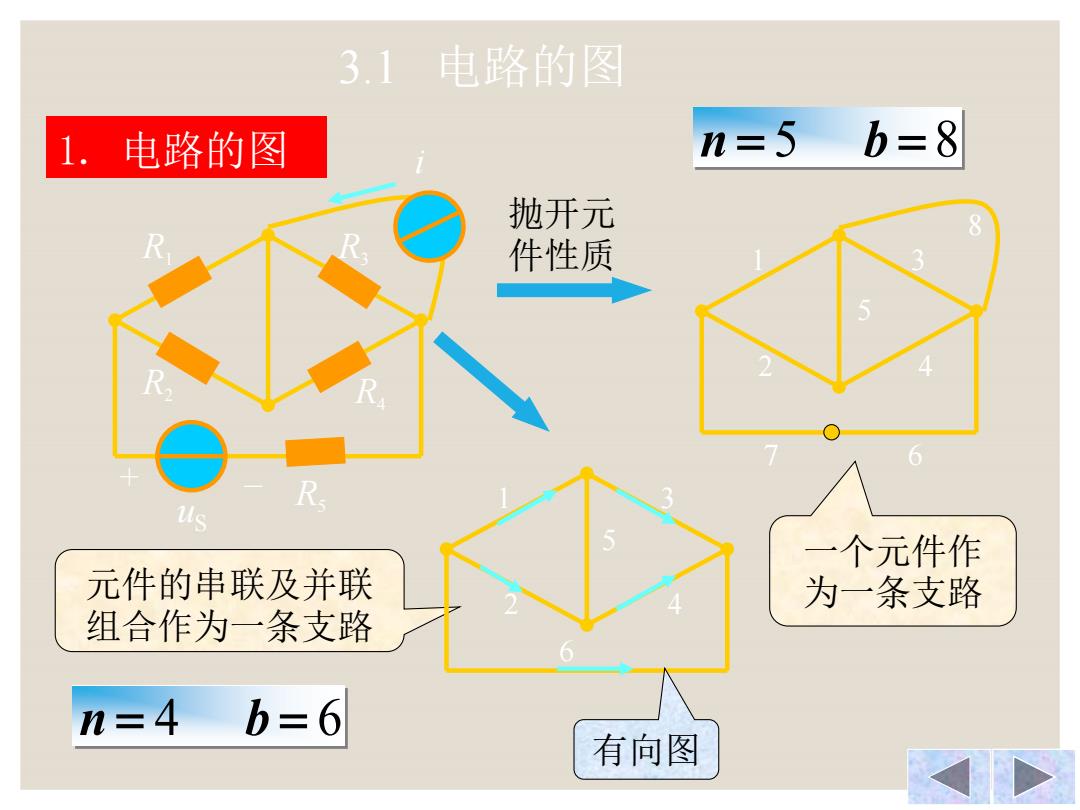
3.1电路的图 1.电路的图 n=5b=8 抛开元 件性质 us 一个元件作 元件的串联及并联 为一条支路 组合作为一条支路 n=4 b=6 有向图
3.1 电路的图 1. 电路的图 R4 R1 R3 R2 R5 uS + _ i 抛开元 件性质 一个元件作 为一条支路 n 5 b 8 元件的串联及并联 组合作为一条支路 n 4 b 6 6 5 4 3 2 1 7 8 5 4 3 2 1 6 有向图

§3-2 KCL和KVL的独立方程数 一、KCL的独立方程数 n个节点的电路 n个KCL方程 个方程中的任何一个方程都可以从其余(n-1)个方程推出来 n个节点的电路 (n-1)个独立的KCL方程 独立节点:与独立方程对应的节点。 任选(n-1)个节点即为独立节点
§32 KCL和KVL的独立方程数 n个KCL方程 一、KCL的独立方程数 n个节点的电路 n个方程中的任何一个方程都可以从其余(n–1)个方程推出 来 n个节点的电路 (n–1)个独立的KCL方程 独立节点:与独立方程对应的节点。 任选(n–1)个节点即为独立节点

二、KVL的独立方程数 1、独立回路 连通图:图G的任意两个结点之间至少存在一条路径。 子图:如果G,的每个结点都是图G中的结点,G,的每条 支路都是G中的支路,则G,是G的子图。 回路: 如果一条路径的起点和终点重合,且经过的其他结 点都相异,这条闭合路径就构成G的一个回路。 树: 连通图G的一个树T,是指G的一个子图, 它必须满足: a 连通的; b 包含G的全部结点; C 不包含回路
二、KVL的独立方程数 1、独立回路 连通图: 树: 图G的任意两个结点之间至少存在一条路径。 子图: 如果 G1 的每个结点都是图G 中的结点,G1 的每条 支路都是G中的支路,则G1 是G 的子图。 如果一条路径的起点和终点重合,且经过的其他结 点都相异,这条闭合路径就构成G的一个回路。 回路: 连通图G的一个树T,是指G的一个子图, 它必须满足: a 连通的; b 包含G的全部结点; C 不包含回路
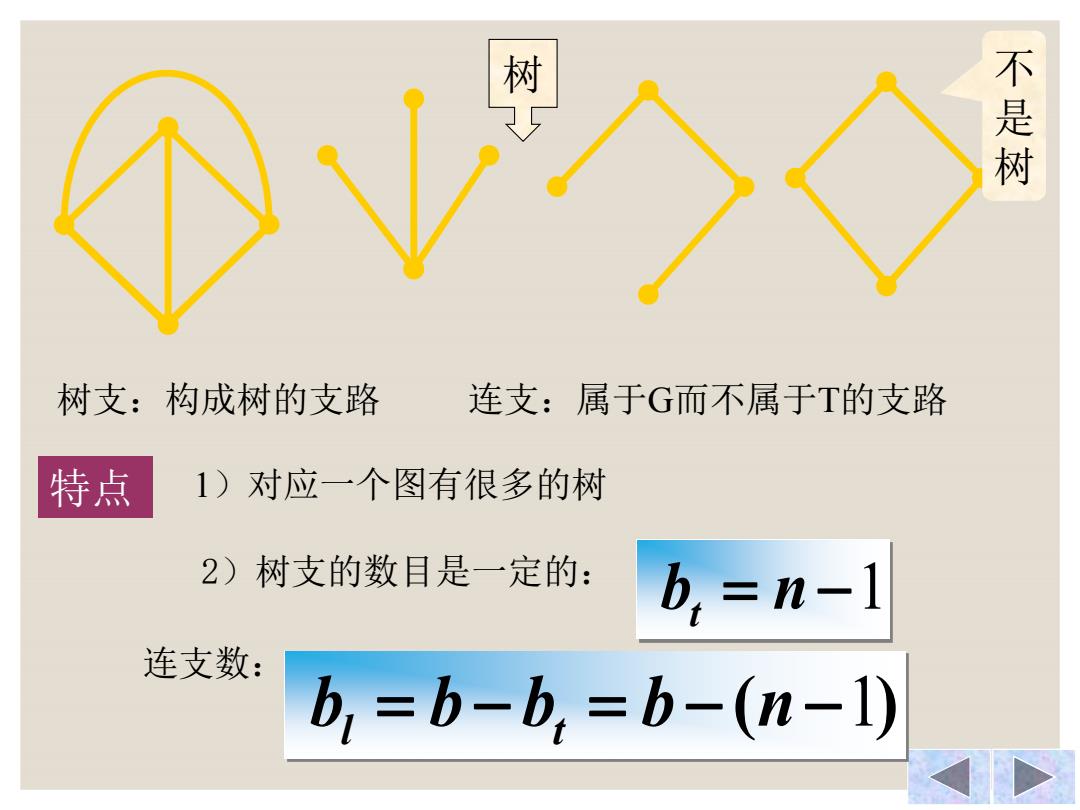
树 不是树 树支:构成树的支路 连支:属于G而不属于T的支路 特点 1)对应一个图有很多的树 2)树支的数目是一定的: b,=n-1 连支数: b,=b-b,=b-(n-1)
树支:构成树的支路 连支:属于G而不属于T的支路 2)树支的数目是一定的: 连支数: 不 是 树 b n 1 t b b b b (n1) l t 树 特点 1)对应一个图有很多的树
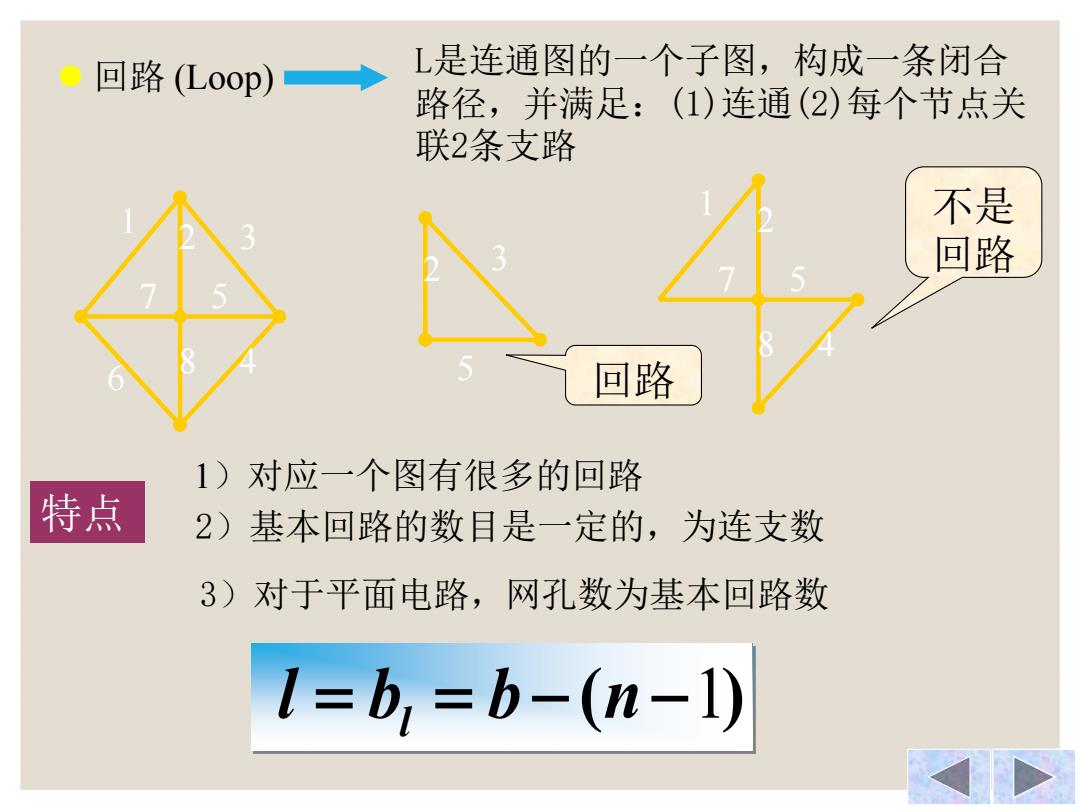
●回路(Loop)◆ L是连通图的一个子图,构成一条闭合 路径,并满足:(1)连通(2)每个节点关 联2条支路 不是 回路 回路 1)对应一个图有很多的回路 特点 2)基本回路的数目是一定的,为连支数 3)对于平面电路,网孔数为基本回路数 1=b,=b-(n-1)
回路 (Loop) L是连通图的一个子图,构成一条闭合 路径,并满足:(1)连通(2)每个节点关 联2条支路 1 2 3 4 5 6 7 8 2 5 3 1 2 4 7 5 8 不是 回路 回路 2)基本回路的数目是一定的,为连支数 l b b (n 1) l 特点 1)对应一个图有很多的回路 3)对于平面电路,网孔数为基本回路数

单连支回路: 基本回路: G的任意一个树,加入一个连支后形成的一个回路 1.除所加连支外均由树支组成: 2.对于一棵树,所有的单连支回路构成基本回路组。 基本回路组是独立回路组; 3.根据基本回路列出的KL方程组是独立方程组; 4.选择不同的树,可以得到不同的基本回路组
3. 根据基本回路列出的KVL方程组是独立方程组; 单连支回路: 基本回路: G的任意一个树,加入一个连支后形成的一个回路. 1. 除所加连支外均由树支组成; 2. 对于一棵树,所有的单连支回路构成基本回路组。 基本回路组是独立回路组; 4. 选择不同的树,可以得到不同的基本回路组