
第4章 电路定理 (Circuit Theorems) 4.1 叠加定理(Superposition Theorem) 4.3 戴维宁定理和诺顿定理 (Thevenin-Norton Theorem)
第4章 电路定理 (Circuit Theorems) 4.1 叠加定理 (Superposition Theorem) 4.3 戴维宁定理和诺顿定理 (Thevenin-Norton Theorem)

)重点: 掌握各定理的内容、适用范围及 如何应用;
重点: 掌握各定理的内容、适用范围及 如何应用;
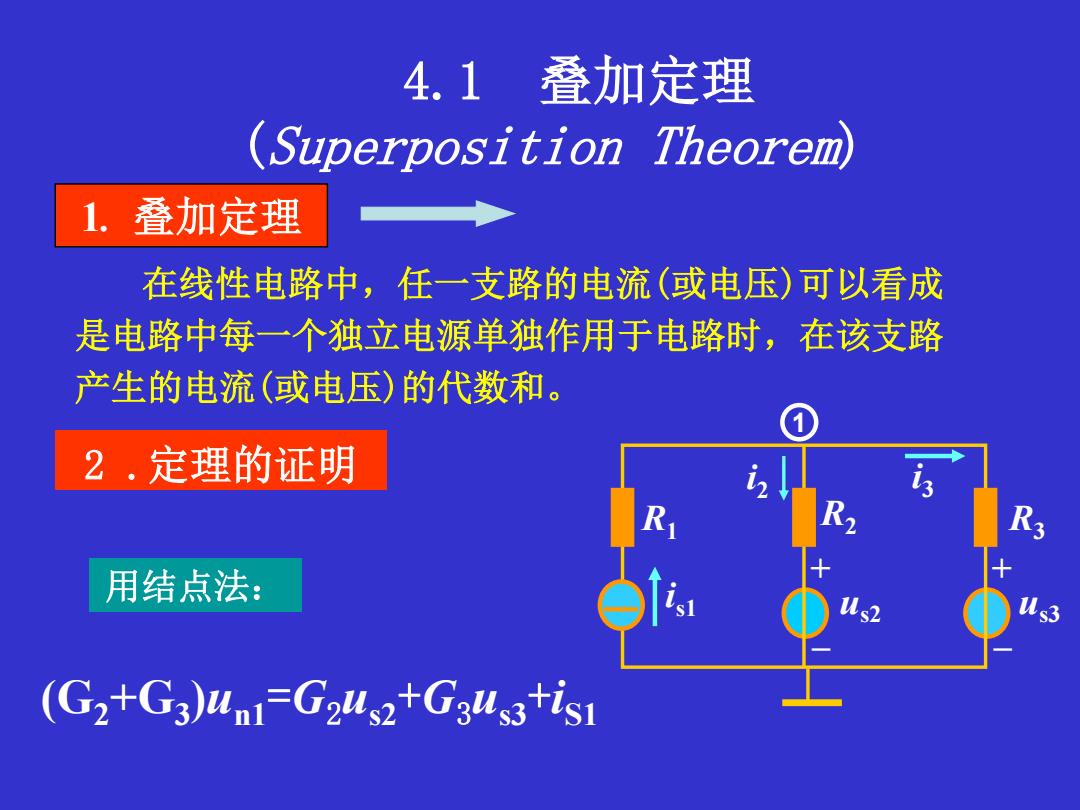
4.1 叠加定理 (Superposition Theorem 1.叠加定理 在线性电路中,任一支路的电流(或电压)可以看成 是电路中每一个独立电源单独作用于电路时,在该支路 产生的电流(或电压)的代数和。 2,定理的证明 用结点法: (G2+G3)unI=G2Us2+G3us3+isI
1. 叠加定理 在线性电路中,任一支路的电流(或电压)可以看成 是电路中每一个独立电源单独作用于电路时,在该支路 产生的电流(或电压)的代数和。 4.1 叠加定理 (Superposition Theorem) 2 .定理的证明 R1 i s1 R2 us2 R3 us3 i2 i3 + – + – 1 用结点法: (G2+G3 )un1 =G2us2+G3us3+iS1
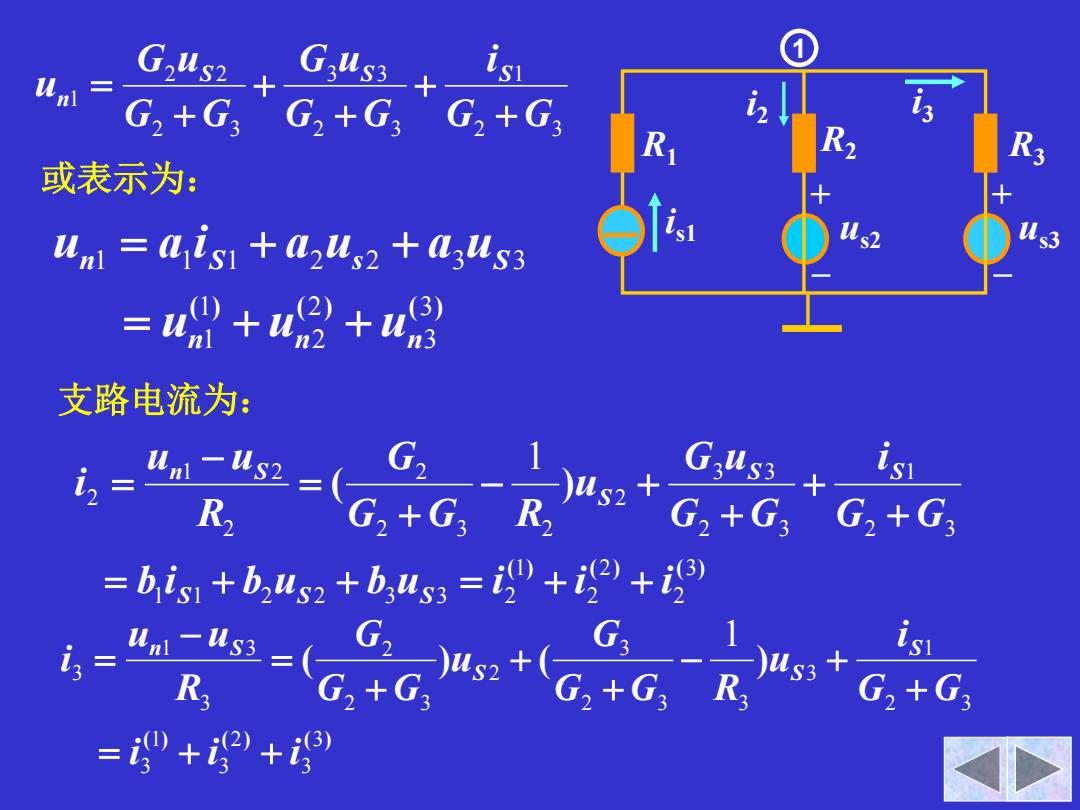
G,us2_ isi G,+G,+G,+G+G,+G i K3 或表示为: um ais aus2 azuss =a州+a+u 支路电流为: g-1 4nms2=(G,+G、R isu R a+88*ad =bis1+b,4s2+b,4s3=++ -*a*0 6-是-aa*。,0 =0+2+40
R 1i s1 R 2us2 R 3us3 i2 i3 +– +– 1 2 3 1 2 3 3 3 2 3 2 2 1 G G i G G G u G G G u u S S S n 或表示为: ( ) ( ) ( ) 33 22 11 1 1 1 2 2 3 3 n n n n S s S u u u u a i a u a u 支路电流为: ( ) ( ) ( ) ( ) 32 22 1 1 1 2 2 3 3 2 2 3 1 2 3 3 3 2 2 3 2 2 2 1 2 2 1 b i b u b u i i i G G i G G G u u G G R G R u u i S S S S S S n S ( ) ( ) ( ) ( ) ( ) 33 23 13 2 3 1 3 2 3 3 3 2 2 3 2 3 1 3 3 1 i i i G G i u G G R G u G G G R u u i S S S n S
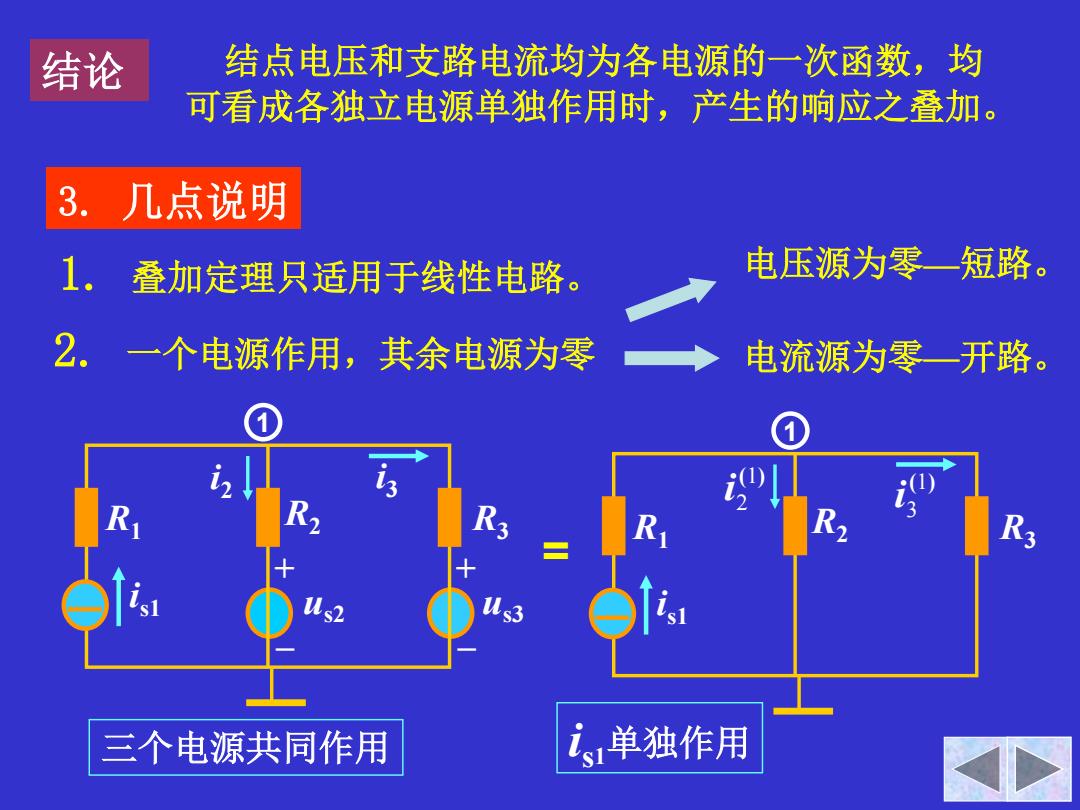
结论 结点电压和支路电流均为各电源的一次函数,均 可看成各独立电源单独作用时,产生的响应之叠加。 3. 几点说明 1. 叠加定理只适用于线性电路。 电压源为零一短路。 2. 一个电源作用,其余电源为零 电流源为零—开路。 三个电源共同作用 i,单独作用
结点电压和支路电流均为各电源的一次函数,均 可看成各独立电源单独作用时,产生的响应之叠加。 结论 3. 几点说明 1. 叠加定理只适用于线性电路。 2. 一个电源作用,其余电源为零 电压源为零—短路。 电流源为零—开路。 R1 i s1 R2 us2 R3 us3 i2 i3 + – + – 1 三个电源共同作用 R1 i s1 R2 R3 1 (1) 2 i (1) 3 i i s1单独作用 =
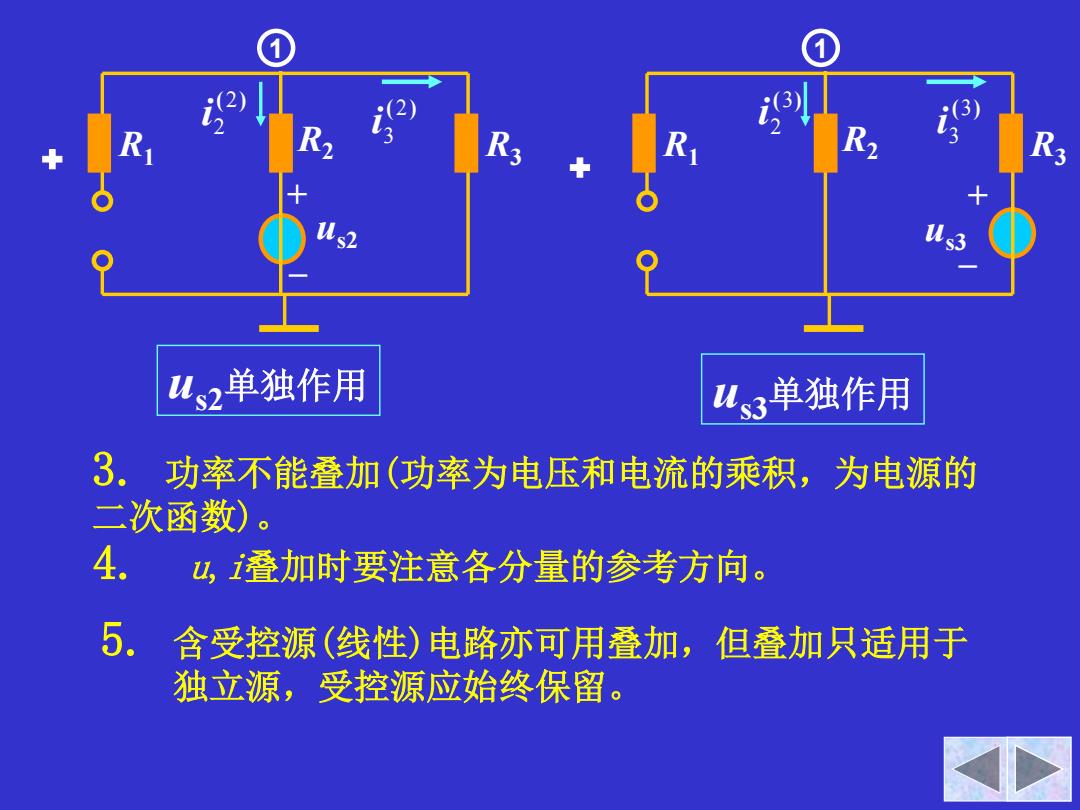
s2 4s2单独作用 43单独作用 3。功率不能叠加(功率为电压和电流的乘积,为电源的 二次函数)。 4. ,叠加时要注意各分量的参考方向。 5. 含受控源(线性)电路亦可用叠加,但叠加只适用于 独立源,受控源应始终保留
+ us2单独作用 us3单独作用 + R1 R2 us2 R3 + – 1 (2) 3 i (2) 2 i R1 R2 us3 R3 + – 1 (3) 2 i (3) 3 i 3. 功率不能叠加(功率为电压和电流的乘积,为电源的 二次函数)。 4. u,i叠加时要注意各分量的参考方向。 5. 含受控源(线性)电路亦可用叠加,但叠加只适用于 独立源,受控源应始终保留
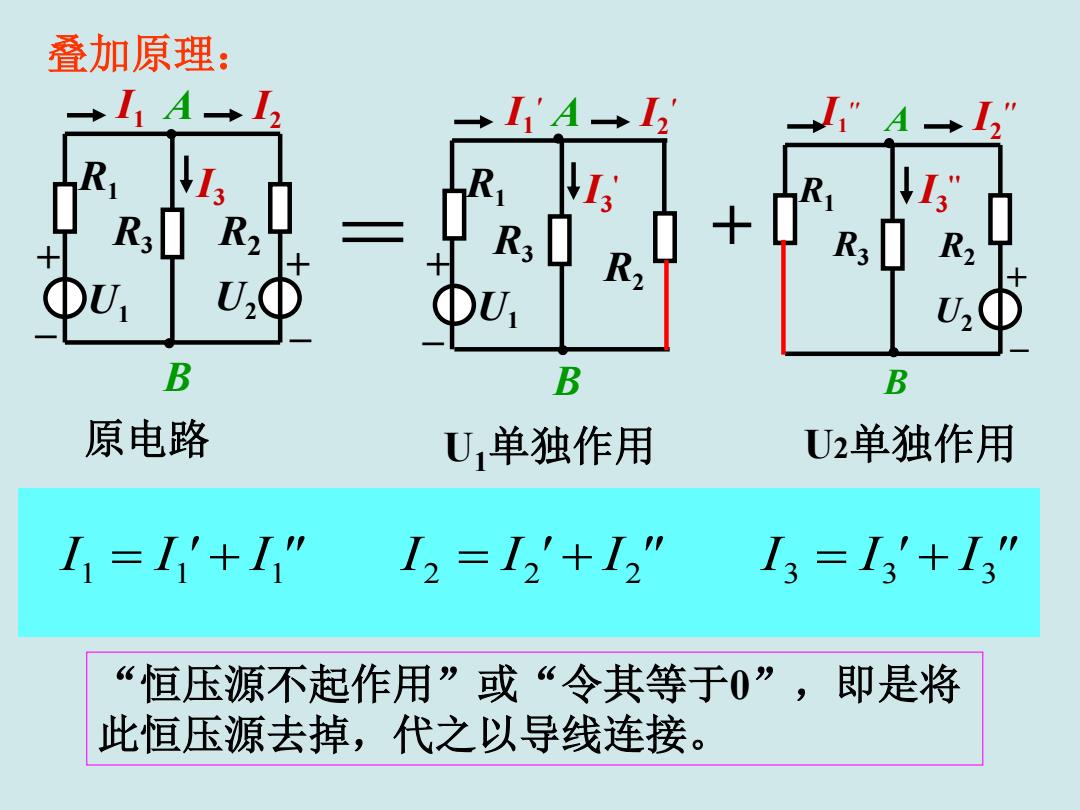
叠加原理: →I1A→I2 →I1'A→2 ”A→2 R; R2 R2 U2 B B B 原电路 U单独作用 U2单独作用 I=I'+I” 2=12'+12” 13=13'+13” “恒压源不起作用”或“令其等于0”,即是将 此恒压源去掉,代之以导线连接
I I ' I " I I ' I " I I ' I " 1 1 1 2 2 2 3 3 3 + B I2 R1 I1 U1 R2 A U2 I3 R3 + _ + _ 原电路 I2 '' R1 I1 '' R2 A B U2 I3 '' R3 + _ U2单独作用 + _ A U1 B I2 ' R1 I1 ' R2 I3 ' R3 U1单独作用 叠加原理: “恒压源不起作用”或“令其等于0”,即是将 此恒压源去掉,代之以导线连接
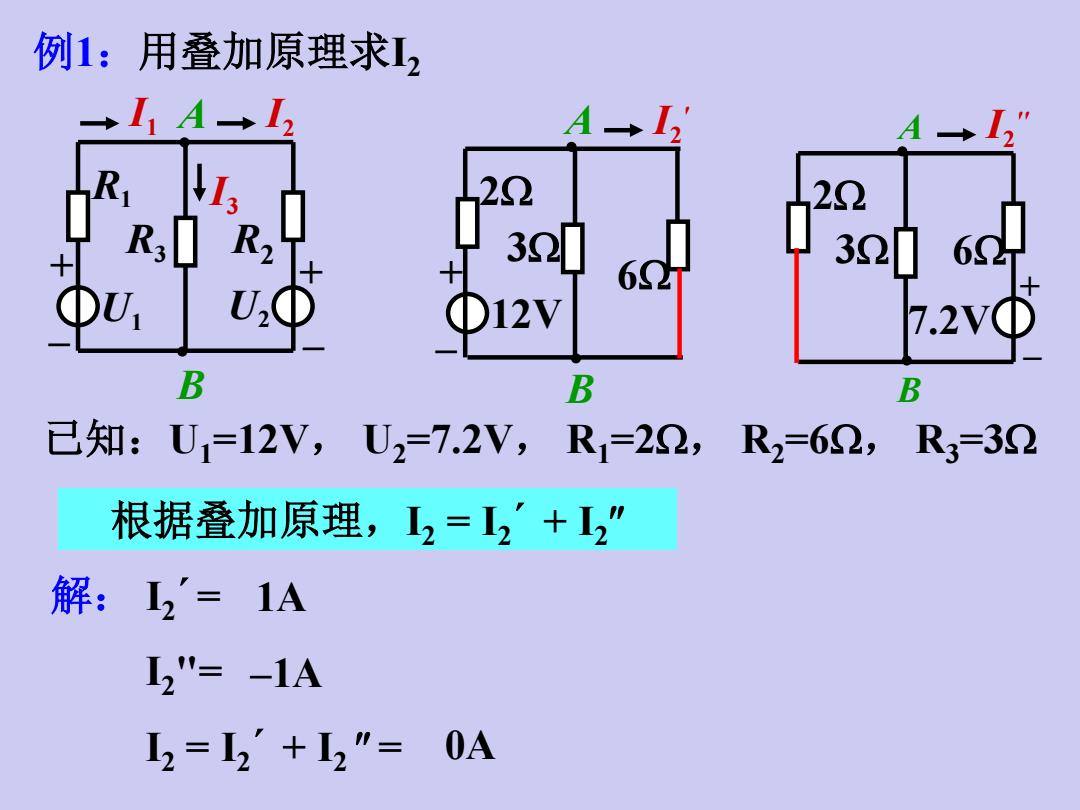
例1:用叠加原理求L, →I1A→I2 A→I2 A→) 13 122 22 R2 32L 6 320 62 U.O B B B 已知:U=12V,U2=7.2V,R1=22,R2=62,R3=32 根据叠加原理,2=2'+2” 解:2'=1A 2"=-1A I2=2+2”= 0A
例1:用叠加原理求I2 B I2 R1 I1 U1 R2 A U2 I3 R3 + _ + _ I2 '' 2 6 A B 7.2V 3 + _ + _ A 12V B I2 ' 2 6 3 已知:U1=12V, U2=7.2V, R1=2, R2=6, R3=3 解: I2 ´ = I2"= I2 = I2 ´ + I2 = 根据叠加原理,I2 = I2 ´ + I2 1A –1A 0A
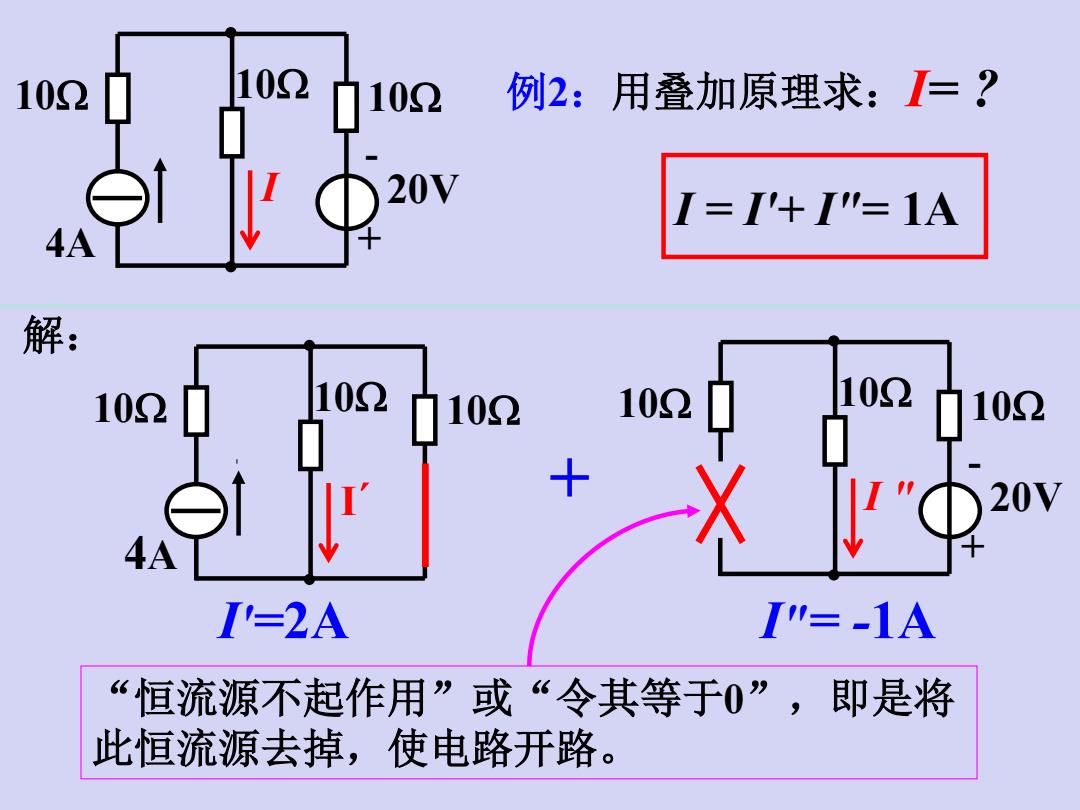
102 102 102 例2:用叠加原理求:=? 20V =I'+I"=1A 4A 解: 102 102 102 102 102 102 20V 4A '=2A "=-1A 恒流源不起作用”或“令其等于0”,即是将 此恒流源去掉,使电路开路
+ - 10 I 4A 20V 10 10 例2:用叠加原理求:I= ? I'=2A I"= -1A I = I'+ I"= 1A + 10 I´ 4A 10 10 + - 10 I " 20V 10 10 解: “恒流源不起作用”或“令其等于0”,即是将 此恒流源去掉,使电路开路

4.叠加定理的应用 82 3A 62 例1 求电压U. 22 3 解 12 12V电源作用: U0=- ×3=-4V 9 3A电源作用:U2)=(6∥3)×3=6 7U=-4+6=2 画出分 8① 62 82 6 电路图 22 32 22 30
4. 叠加定理的应用 例1 求电压U. 8 12V 3A + – 6 2 3 + - U 8 3A 6 2 3 + - U(2) 8 12V + – 6 2 3 + - U(1) 画出分 电路图 + 12V电源作用: U 3 4V 9 (1) 12 3A电源作用: U (6// 3) 3 6V (2) U 4 6 2V 解