石河子大 常用络合物 分析化学中的络合物 简单络合物 螯合物 多核络合物 H2 H2 N H2C CH2 Cu(NH3) Cu OH [(H2O)4Fe Fe(O)4]4 H2C CH2 OH N N H2 H2 ■只有一个配位原子同中 ☐有两个以上配位原子同 ■含有有两个以上中 心离子配合,称单齿配体。 中心离子配合一多齿配体。心离子的配合物。 ■中心离子和单齿配体配 ■中心离子和多齿配体配 合,没有环状结构。 合,形成环状结构
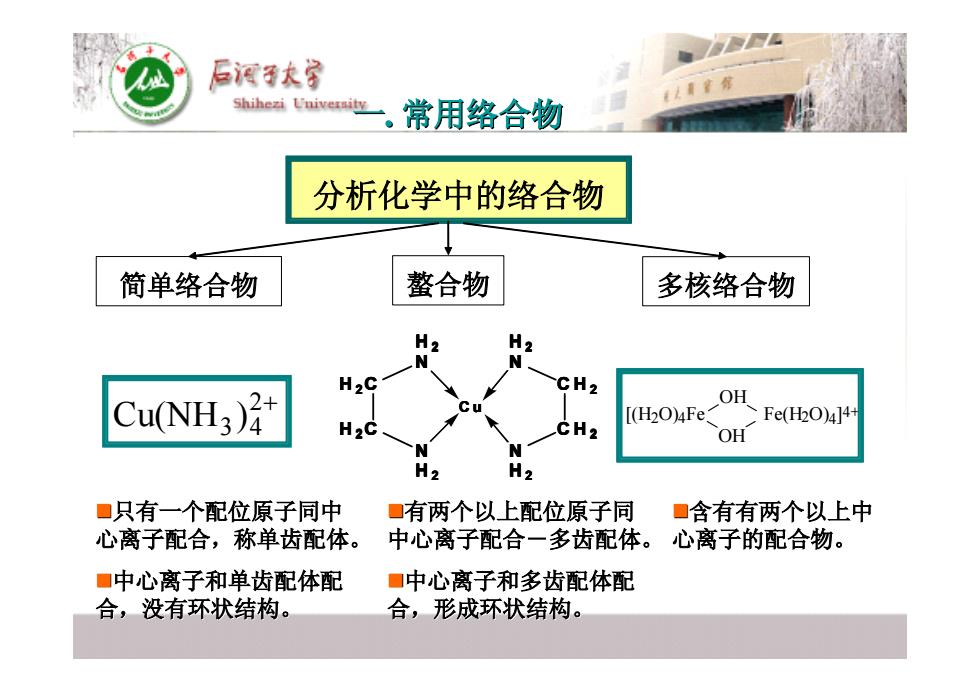
分析化学中的络合物 简单络合物 2+ 3 4 Cu(NH ) 螯合物 多核络合物 [(H2O)4Fe OH OH Fe(H2O)4]4+ �只有一个配位原子同中 只有一个配位原子同中 心离子配合,称单齿配体。 心离子配合,称单齿配体。 �中心离子和单齿配体配 中心离子和单齿配体配 合,没有环状结构。 合,没有环状结构。 �有两个以上配位原子同 有两个以上配位原子同 中心离子配合-多齿配体。 中心离子配合-多齿配体。 �中心离子和多齿配体配 中心离子和多齿配体配 合,形成环状结构。 合,形成环状结构。 �含有有两个以上中 含有有两个以上中 心离子的配合物。 心离子的配合物。 C H 2 C H 2 H 2 N N H 2 C u H 2C H 2C H 2 N N H 2 一. 常用络合物
后酒子大 Shihezi University 络合反应在分析化学中应用广泛 沉淀反应例如,8羟基喹啉与镁离子生成螯合物沉淀: Mg(H2O)62++2 +2H++4H20 掩蔽反应 例如,用KCN掩蔽Z+,消除其对EDTA滴定 Pb2+的千扰。 Zn2++4CN-=Zn(CN)
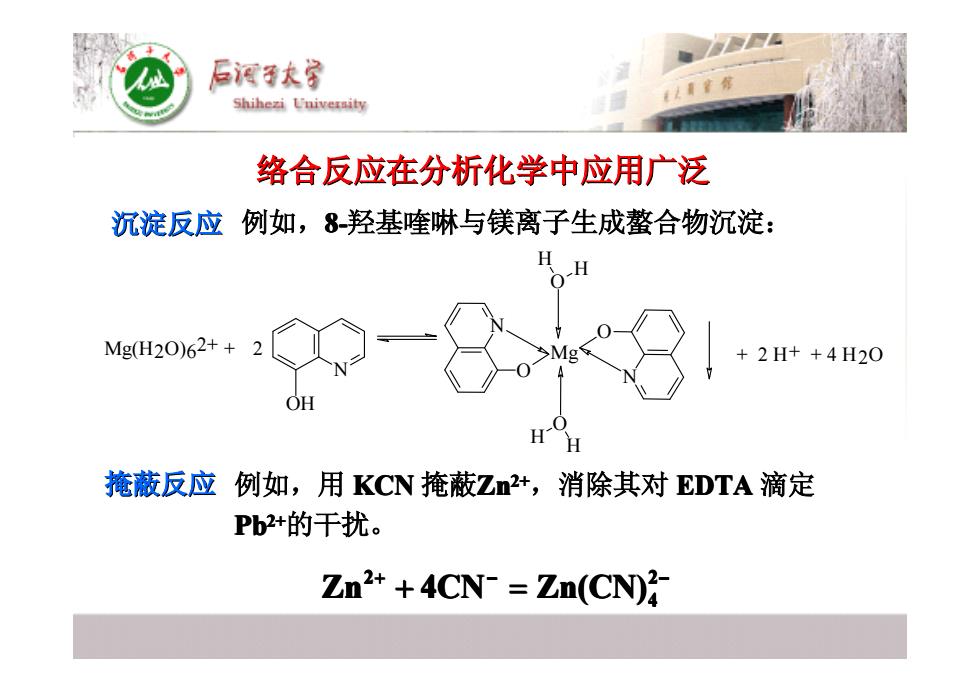
络合反应在分析化学中应用广泛 络合反应在分析化学中应用广泛 沉淀反应 例如,8-羟基喹啉与镁离子生成螯合物沉淀: 羟基喹啉与镁离子生成螯合物沉淀: Mg(H2O)62+ + N OH 2 N O N O Mg O H H O H H + 2 H+ + 4 H2O 掩蔽反应 例如,用 KCN 掩蔽Zn2+2+,消除其对 EDTA 滴定 Pb2+2+的干扰。 + − − + = 2 4 2 Zn 4CN Zn(CN)
后酒子太学 Shihezi University 显色反应 例如,邻二氮氯 Fe2++ NN> 菲显色分光光 度法测定铁: 邻二氮菲 桔红色入max 滴定反应 例如:EDTA络合滴定 CH 法测定水的硬度所形成 ●a 的Ca2+EDTA络合物
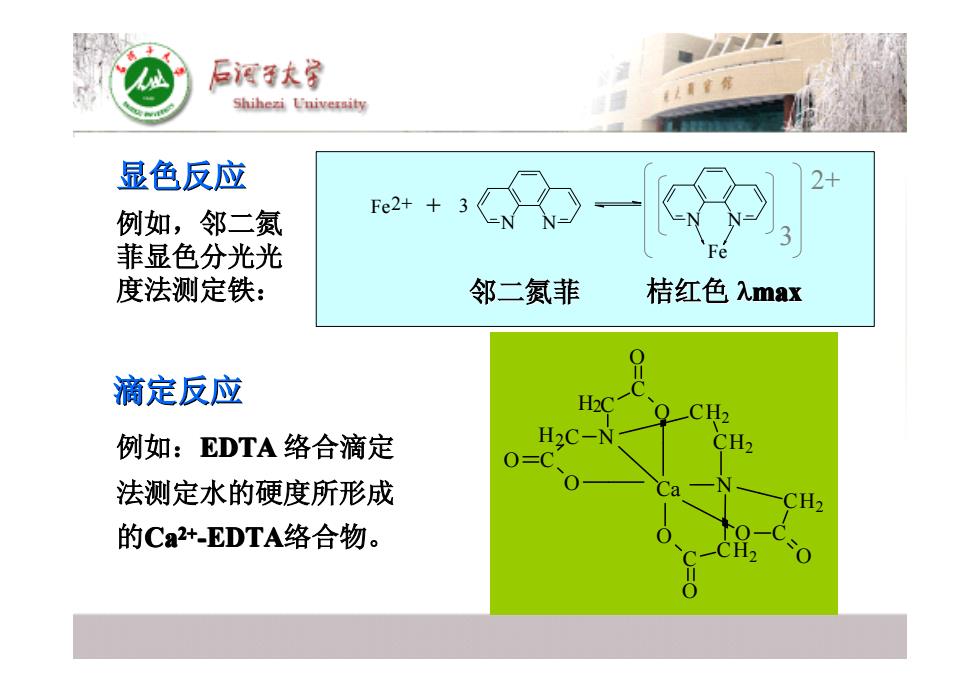
3 3 Fe2+ 3 N N + N N Fe 2+ 邻二氮菲 桔红色 λmax 例如,邻二氮 菲显色分光光 度法测定铁: 显色反应 滴定反应 例如:EDTA 络合滴定 法测定水的硬度所形成 法测定水的硬度所形成 的Ca2+2+ -EDTA络合物。 C C N C C O O O O CH2 CH2 CH2 O O C C CH2 N O O Ca H2 H2

酒节大家 Shihezi University 口络合滴定法(又称配位滴定法)是以络合反应和络 合平衡为基础的滴定分析方法。 ■它常用络合剂作为标准溶液直接或间接滴定被测物 质,并选用适当的指示剂指示滴定终点。 例如:以EDTA标准溶液作为滴定剂测定水的总硬 度,以及连续测定溶液中Pb、Bi的含量
� 它常用络合剂作为标准溶液直接或间接滴定被测物 它常用络合剂作为标准溶液直接或间接滴定被测物 质,并选用适当的指示剂指示滴定终点。 质,并选用适当的指示剂指示滴定终点。 � 络合滴定法(又称配位滴定法)是 络合滴定法(又称配位滴定法)是以络合反应和络 合平衡为基础的滴定分析方法。 为基础的滴定分析方法。 例如:以EDTA标准溶液作为滴定剂测定水的总硬 标准溶液作为滴定剂测定水的总硬 度,以及连续测定溶液中 度,以及连续测定溶液中Pb、Bi的含量

后酒子太学 Shihezi University 用于滴定分析的络合反应应具备的条件: 1)形成络合物的稳定常数要大。 2)在一定反应条件下,只形成一种络合数的化合物。 3)络合反应要快速,有确定终点的方法
用于滴定分析的络合反应应具备的条件: 用于滴定分析的络合反应应具备的条件: 1)形成络合物的稳定常数要大。 )形成络合物的稳定常数要大。 2) 在一定反应条件下,只形成一种络合数的化合物。 在一定反应条件下,只形成一种络合数的化合物。 3)络合反应要快速,有确定终点的方法。 )络合反应要快速,有确定终点的方法
E酒子大学 Shihezi University 常用螯合剂:氨羧络合剂是一类含有氨基二乙 酸 N(CH,COOD2基团的有机化合物,其分子中含有氨基 氮和羧基氧两种络合能力很强的络合原子(系多齿配位体),可以 和很多金属离子形成稳定的络合物。 HOOCH2C CH2COO EDTA NHtC—CNHt H2 H2 OOCH>C CH2COOH 乙二胺四乙酸LY) 乙二胺四乙酸二钠盐N2H2Y
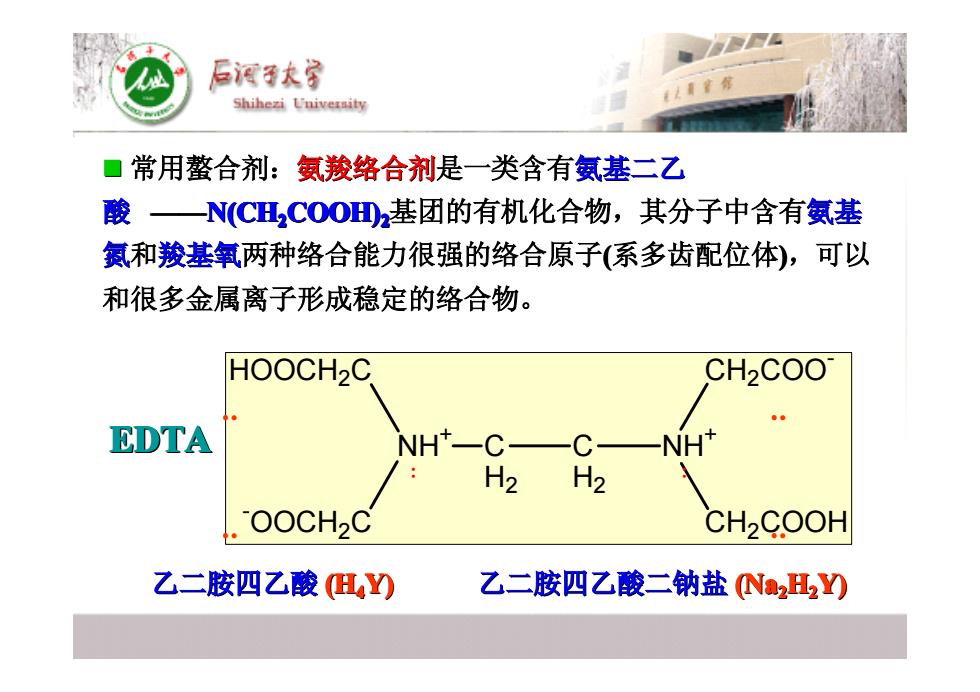
EDTA 乙二胺四乙酸 (H44Y) 乙二胺四乙酸二钠盐 乙二胺四乙酸二钠盐 (Na22H22Y) NH+ C H2 C H2 HOOCH2C -OOCH2C NH+ CH2COOH CH2COO- : : : : ·· ·· � 常用螯合剂:氨羧络合剂是一类含有氨基二乙 酸 ——N(CH22COOH) 22基团的有机化合物,其分子中含有 基团的有机化合物,其分子中含有氨基 氮和羧基氧两种络合能力很强的络合原子 两种络合能力很强的络合原子(系多齿配位体),可以 和很多金属离子形成稳定的络合物 和很多金属离子形成稳定的络合物
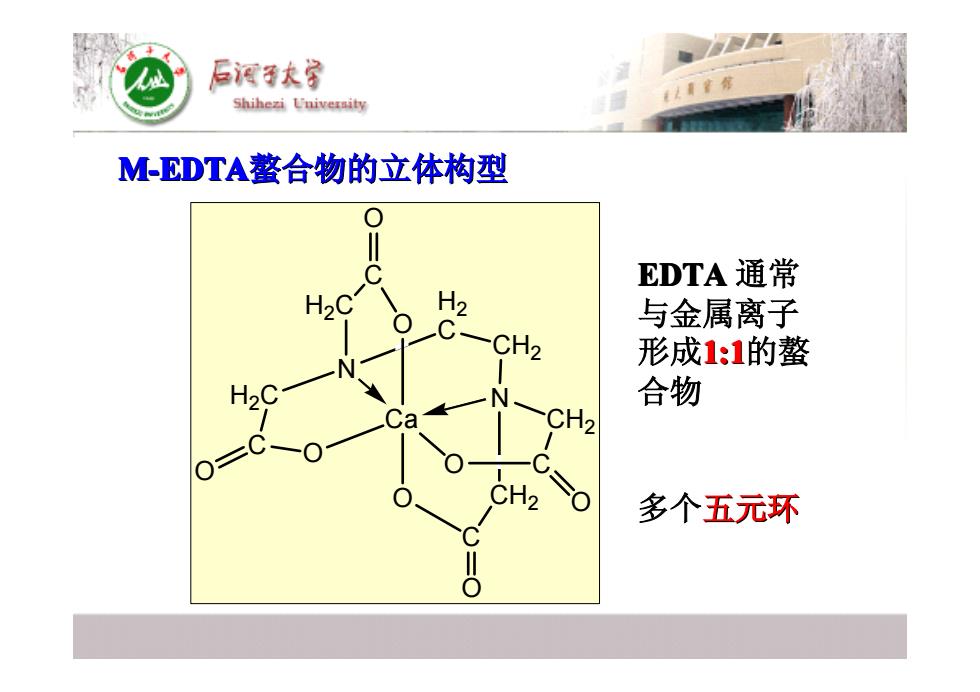
后酒子太学 Shihezi University M-EDTA螯合物的立体构型 EDTA通常 H2C H2 与金属离子 形成1:1的整 合物 多个五元环
M-EDTA螯合物的立体构型 螯合物的立体构型 O Ca O O N O N C O H2C H2 C CH2 CH2 C C CH2 C H2C O O O EDTA 通常 与金属离子 形成1:1的螯 合物 多个五元环

酒节大家 Shihezi University 二 络合平衡 p172 在一定条件下,络合物形成和解离达到相对平衡,称为 络合平衡。 1,络合物的稳定常数(瓜,P) M+Y=MY [MY] [M][Y] KY称为绝对稳定常数,简称稳定常数。 ■KY越大,络合物越稳定。 ■不稳定常数(解离常数)=1KY
二. 络合平衡 p172 在一定条件下,络合物形成和解离达到相对平衡,称为 在一定条件下,络合物形成和解离达到相对平衡,称为 络合平衡。 [MY] [M][Y] KMY= � KMYMY越大,络合物越稳定。 越大,络合物越稳定。 � 不稳定常数(解离常数) 不稳定常数(解离常数)=1/KMYMY。 KMY MY称为绝对稳定常数,简称稳定常数。 称为绝对稳定常数,简称稳定常数。 1. 络合物的稳定常数 络合物的稳定常数 (K, β ) M + Y = MY M + Y = MY M + Y = MY M + Y = MY M + Y = MY M + Y = MY M + Y = MY M + Y = MY

后酒子太学 Shihezi University 逐级络合物ML,在溶 逐级稳定常数K 液中是分级形成的 逐级累积稳定常数B [ML] M+L=ML [ML] [M]IL] B-K- MIL] ML+L=ML2 ML] [ML] MLIL] 2=K= [MILP ●●● ML] ML+L=MLn K ML] [ML-IIL] B-KGK- [MIILI 【表示相邻络合 B表示络合物与 物之间的关系 配体之间的关系
逐级稳定常数 Kii ● ● ● ● ● ● ● ● ● K 表示相邻络合 物之间的关系 M + L = ML M + L = ML M + L = ML M + L = ML M + L = ML M + L = ML M + L = ML M + L = ML ML + L = ML ML + L = ML ML + L = ML ML + L = ML ML + L = ML ML + L = ML ML + L = ML ML + L = ML22 逐级累积稳定常数 逐级累积稳定常数 β β 表示络合物与 配体之间的关系 [ML] [M][L] K11= [ML22] [ML][L] [ML][L] [ML][L] [ML][L] [ML][L] [ML][L] [ML][L] [ML][L] K22= [MLnn] [MLn-1 n-1][L] Knn = [ML] [M][L] β11=K11= [ML22] [M][L] 22 β22=K11K22= [MLnn] [M][L]nn βnn =K11K2 2···Knn = 逐级络合物MLnn在溶 液中是分级形成的 液中是分级形成的 ML + L = ML ML + L = ML ML + L = ML ML + L = ML ML + L = ML ML + L = ML ML + L = ML ML + L = MLnn

酒节大家 Shihezi University 2。溶液中各级络合物的分布 M+L=ML [ML]=B[M][L] ML+L=ML ML2]=B2[M][L2 MLp1+L=MLp [ML]=BIM][L CM-[M]+[ML]+[ML2]+.+[ML] =[MI(1+B1[L+B2[L2.+B[L
2. 溶液中各级络合物的分布 溶液中各级络合物的分布 [ML] = β 1 1[M] [L] [M] [L] [M] [L] [M] [L] [M] [L] [M] [L] [M] [L] [M] [L] [ML22] = β 2 2[M] [L] [M] [L] [M] [L] [M] [L] [M] [L] [M] [L] [M] [L] [M] [L] 22 . [MLnn]= β n n[M] [L]nn . M + L = ML M + L = ML M + L = ML M + L = ML M + L = ML M + L = ML M + L = ML M + L = ML ML + L = ML ML + L = ML ML + L = ML ML + L = ML ML + L = ML ML + L = ML ML + L = ML ML + L = ML22 MLn-1 n-1+ L = MLnn cMM=[M]+[ML]+[ML =[M]+[ML]+[ML =[M]+[ML]+[ML =[M]+[ML]+[ML =[M]+[ML]+[ML =[M]+[ML]+[ML =[M]+[ML]+[ML =[M]+[ML]+[ML22]+.+[MLnn] =[M](1+ =[M](1+ =[M](1+ =[M](1+ =[M](1+ =[M](1+ =[M](1+ =[M](1+ β 11 [L]+ β 22 [L] 22+.+ β nn [L]nn )