
石河子大学化学化工学院分析化学教案 授课 第二章 内容 误差和分析数据的处理 课时安排10学时 1.掌握有关误差的基本概念及表示方法: 教学 2.掌握有效数字的表示和运算规则: 日的 3了解实:哈新根的分布特占和分析数据的处理! 要求 4.正确应用F检验和检验对分析方法和结果作出评价 教学 重点 难点 重点:误差的正态分布:有效数字及运算规则:下检验、t拾验 教学 方法 讲授为主,启发式和互动式相结合: 手段 多媒体教学与传统教学相结合。 误差及其产生的原因 1 系统误差 2.偶然误差 ,测定值的准确度与精密度 1.准确度与误差: 2.精密度与偏差:3.精密度与准确度的关系。 三、随机误差的正态分布 1数据处理中常用名词的含义: 2测定值的频数分布: 随机误差的正态分布 四、有限测定数据的统计处理 1.置信度与μ的置信区间: 2.可疑值的取舍: 3.分析方法准确度的检验。 4.分析结果的表示方法。 五、有效数字及其运算规则 1.有效数字的意义及位数: 2.数字修约规则 有效数字的运算规则: 4.有效数字运算规则在分析化学中的应用 六、提高分析结果准确度的方法 1.化学分析中对准确度的要求: 2.分析准确度的检验: 3.提高分析结果准确度的方法。 课外 学习 根据本章要求,查阅相关资料,并上课程网复习巩固,完成相应作业。 要求 教学 后记
石河子大学化学化工学院-分析化学教案 3 授课 内容 第二章 误差和分析数据的处理 课时安排 10 学时 教学 目的 要求 1. 掌握有关误差的基本概念及表示方法; 2. 掌握有效数字的表示和运算规则; 3. 了解实验数据的分布特点和分析数据的处理; 4. 正确应用 F 检验和 t 检验对分析方法和结果作出评价。 教学 重点 难点 重点:误差的正态分布;有效数字及运算规则;F 检验、t 检验。 教学 方法 手段 讲授为主,启发式和互动式相结合; 多媒体教学与传统教学相结合。 教 学 内 容 提 纲 一、误差及其产生的原因 1. 系统误差; 2. 偶然误差。 二、测定值的准确度与精密度 1. 准确度与误差; 2. 精密度与偏差; 3. 精密度与准确度的关系。 三、随机误差的正态分布 1. 数据处理中常用名词的含义; 2. 测定值的频数分布; 3. 随机误差的正态分布。 四、有限测定数据的统计处理 1. 置信度与μ的置信区间; 2. 可疑值的取舍; 3. 分析方法准确度的检验。 4. 分析结果的表示方法。 五、有效数字及其运算规则 1. 有效数字的意义及位数; 2. 数字修约规则; 3. 有效数字的运算规则; 4. 有效数字运算规则在分析化学中的应用。 六、提高分析结果准确度的方法 1. 化学分析中对准确度的要求; 2. 分析准确度的检验; 3. 提高分析结果准确度的方法。 课外 学习 要求 根据本章要求,查阅相关资料,并上课程网复习巩固,完成相应作业。 教学 后记

石河子大学化学化工学院分析化学教案 第三章误差和分析数据的处理 进程: §31误差及其产生的原因 一、系续兼 指由于某些固定原因所导致的误差 特点:“重复性”、“单向性”、“可测性”。 1.仪器和试剂引起的误差 由于仪器本身的缺陷所造成的误差叫仪器误差。 由于试剂不纯或蒸馏水中含有微量杂质而引起的误差叫试剂误差。 2.个人操作上引起的误差 由于操作不当而引起的误差称为操作误差。 产生个人误差的原因:一是由于个人观察判断能力的缺陷或不良习惯引起的:二是来源 于个人的偏见或一种先入为主的成见。 操作误差与个人误差,其数值可能因人而异,但对同一个操作者来说基本上是恒定的, 因此,也可以统称为个人误差。 3.方法误差 方法误差是由所采用的分析方法本身的固有特性所引起的,是由分析系统的化学或物理 化学性质所决定的,无论分析者操作如何熟练和小心,这种误差总是难免的。 方法误差的来源有: ①反应不能定量地完成或者有副反应: ②干扰成分的存在 ③在重量分析中沉淀的溶解损失,共沉淀和后沉淀的现象,灼烧沉淀时部分挥发损失或 称量形式具有吸湿性等等。 ④在滴定分析中,滴定终点与化学计量点不相符。 系统误差的性质可以归钠为三点: ①系统误差会在多次测定中重复出现 ②系统误差具有单向性 ③系统误差的数值基本是恒定不变的。 二、偶然误差 指由于某些偶然的、微小的和不可知的因素所引起的误差。 举一个最简单的使用天平称重的例子:取一个瓷坩埚,在同一天平上用同一砝码进行称 重,得到下面的克数 29.3465 29.3463 29.3464 29.3466 为什么四次称重数据会不同呢? ①读取天平指针读数时,总不免偏左或偏右一点,天平本身有一定的变动性,这是无法 控制的 ②天平箱内温度的微小变化,坩埚和砝码上吸附若微量水份的变化: ③空气中尘埃降落速度的不恒定: ④其它未确定因素。 正态分布有三种性质:①离散性:②集中趋势:③对称性。(见书图)
石河子大学化学化工学院-分析化学教案 4 第三章 误差和分析数据的处理 进程: §3-1 误差及其产生的原因 一、系统误差 指由于某些固定原因所导致的误差。 特点:“重复性”、“单向性”、“可测性”。 1.仪器和试剂引起的误差 由于仪器本身的缺陷所造成的误差叫仪器误差。 由于试剂不纯或蒸馏水中含有微量杂质而引起的误差叫试剂误差。 2.个人操作上引起的误差 由于操作不当而引起的误差称为操作误差。 产生个人误差的原因:一是由于个人观察判断能力的缺陷或不良习惯引起的;二是来源 于个人的偏见或一种先入为主的成见。 操作误差与个人误差,其数值可能因人而异,但对同一个操作者来说基本上是恒定的, 因此,也可以统称为个人误差。 3.方法误差 方法误差是由所采用的分析方法本身的固有特性所引起的,是由分析系统的化学或物理 化学性质所决定的,无论分析者操作如何熟练和小心,这种误差总是难免的。 方法误差的来源有: ①反应不能定量地完成或者有副反应; ②干扰成分的存在; ③在重量分析中沉淀的溶解损失,共沉淀和后沉淀的现象,灼烧沉淀时部分挥发损失或 称量形式具有吸湿性等等。 ④在滴定分析中,滴定终点与化学计量点不相符。 系统误差的性质可以归纳为三点: ①系统误差会在多次测定中重复出现; ②系统误差具有单向性; ③系统误差的数值基本是恒定不变的。 二、偶然误差 指由于某些偶然的、微小的和不可知的因素所引起的误差。 举一个最简单的使用天平称重的例子:取一个瓷坩埚,在同一天平上用同一砝码进行称 重,得到下面的克数: 29.3465 29.3463 29.3464 29.3466 为什么四次称重数据会不同呢? ①读取天平指针读数时,总不免偏左或偏右一点,天平本身有一定的变动性,这是无法 控制的; ②天平箱内温度的微小变化,坩埚和砝码上吸附着微量水份的变化; ③空气中尘埃降落速度的不恒定; ④其它未确定因素。 正态分布有三种性质:①离散性;②集中趋势;③对称性。 (见书图)

石河子大学化学化工学院分析化学教案 课堂抽问:P.721题 §3-2测定值的准确度与精密度 一、准确度与误差 准确度是测定值与真实值的符合程度,用误差表示。 ()绝对误差:指测得值与真实值之差。即 绝对误差(Ea) 值(X) 真实值(T) 相对误差(8)-测得值其实值x100%=x100% 真买值(T) 例如,用分析天平称量两个试样,称得1号为1.7542g,2号为0.1754g。假定二者的真 实重量各为1,7543g和0.1755g,则两者称量的绝对误差分别为: 1号:E1=1.7542-1.7543=-0.0001(g) 2号:E2=0.1754-0.1755=-0.0001(g) 者称量的相对误差分别为: 1号 g1=-0.0001 17543x100%=-0.0579% 2号: B,=-0001×10%=-0.057% 0.1755 二、精密度与偏差 在相同条件下多次测定结果相互吻合的程度就叫精密度,用偏差表示。 1.绝对偏差(d) 绝对偏差d,)=个别测得值x)-测得平均值x n 2.相对偏差 相对偏差%= 绝对偏差2×10%=五-×100% 平均值 5
石河子大学化学化工学院-分析化学教案 5 课堂抽问:P.72 1 题 §3-2 测定值的准确度与精密度 一、准确度与误差 准确度是测定值与真实值的符合程度,用误差表示。 ⑴ 绝对误差:指测得值与真实值之差。即 绝对误差(Ea)= 测得值(Xi)- 真实值(T) ⑵ 相对误差:指误差在分析结果中所占的百分率或千分率。 例如,用分析天平称量两个试样,称得 1 号为 1.7542g,2 号为 0.1754g。假定二者的真 实重量各为 1.7543g 和 0.1755g,则两者称量的绝对误差分别为: 1 号: E1=1.7542-1.7543 = -0.0001(g) 2 号: E2 = 0.1754-0.1755 = -0.0001(g) 两者称量的相对误差分别为: 1 号: 2 号: 二、精密度与偏差 在相同条件下多次测定结果相互吻合的程度就叫精密度,用偏差表示。 1. 绝对偏差(di) 2. 相对偏差

石河子大学化学化工学院分析化学教案 相对偏差%。两次测得值之差 平均值一×100% 3.算术平均偏差(d) 算术平均偏差豆.-内习+5-习k-司 4.相对平均偏差 相对平均偏差= 算术平均偏差园×100% 算术平均值x) 5.标准偏差 标准偏S= d+d+.+d n-1 n-1 E+++.+E既 ∑x-47 n 6.相对标准偏差(变异系数) 柜对标准滨莲一受 7.平均值的标准偏差 5= S= √n 三、准确度和精密度的关系 6
石河子大学化学化工学院-分析化学教案 6 3.算术平均偏差( ) 4.相对平均偏差 5.标准偏差 6.相对标准偏差(变异系数) 7.平均值的标准偏差 三、准确度和精密度的关系 d

石河子大学化学化工学院分析化学教案 真价3r.40 甲:准确度和精密度均较好: 乙:精密度好,准确度不高: 丙:准确度和精密度均较差; 丁:精密度莲,准确度不可 36.036.502.0 结论:精密度高是保证准确度高的先决条件:但精密度高不一定准确度就高:若精密度 很低,说明测定结果不可靠,在这种情况下,自然失去了衡量准确度的前提。所以在评价分 析结果时,必须将系统误差和偶然误差的影响结合起来考虑,以提高分析结果的准确度。 四、公差 “公差”是生产部门对分析结果允许误差的一种表示方法。 例如:测定钢中含S量的公差范围为:(武大P13) 含S量% 公差% ≤0.02 ±0.002 0.02-0.05 ±0004 005-010 ±0006 0.10-0.20 ±0.01 ≥0.20 ±0.015 如果试样含S量为0.032%,而测得结果为0.035%,即符合公差的要求(因含S0.032% 是属于含S0.02~0.05%这个范围,它的公差是±0.004)即测得值在0.032±0.004这个范围 内的,都符合要求。 如果分析结果的误差超出公差的范围,就叫超差,就应重作。公差范围的确定,一般是 根据生产的需要和具体情况来确定, 讨论: ·P.722、3、9题 §3-3随机误差的正态分布 一、数据处理中常用名词的含义 1.总体、样本和个体 在统计学中,所研究对象的全体称为总体(又叫母体),其中的一个基本单元称为个体。 从总体中随机抽取出来的部分个体的集合体称为样本(又叫子样)。 2.样本容量 样本中所含数据(如测定值)的个数称为样本容量,用表示。 3.算术平均值(前已讲) 4.中位数(M) 中位数(M)是指将一组测定值按一定大小顺序排列时的中间项的数值。 5,差方 测定值对平均值偏差的平方的加和叫差方和。即
石河子大学化学化工学院-分析化学教案 7 结论:精密度高是保证准确度高的先决条件;但精密度高不一定准确度就高;若精密度 很低,说明测定结果不可靠,在这种情况下,自然失去了衡量准确度的前提。所以在评价分 析结果时,必须将系统误差和偶然误差的影响结合起来考虑,以提高分析结果的准确度。 四、公差 “公差”是生产部门对分析结果允许误差的一种表示方法。 例如:测定钢中含 S 量的公差范围为:(武大 P.13) 含 S 量% 公差% ≤0.02 ±0.002 0.02~0.05 ±0.004 0.05~0.10 ±0.006 0.10~0.20 ±0.01 ≥0.20 ±0.015 如果试样含 S 量为 0.032%,而测得结果为 0.035%,即符合公差的要求(因含 S 0.032% 是属于含 S 0.02~0.05%这个范围,它的公差是±0.004)即测得值在 0.032±0.004 这个范围 内的,都符合要求。 如果分析结果的误差超出公差的范围,就叫超差,就应重作。公差范围的确定,一般是 根据生产的需要和具体情况来确定。 • 讨论: • P.72 2、3、9 题 §3-3 随机误差的正态分布 一、数据处理中常用名词的含义 1.总体、样本和个体 在统计学中,所研究对象的全体称为总体(又叫母体),其中的一个基本单元称为个体。 从总体中随机抽取出来的部分个体的集合体称为样本(又叫子样)。 2.样本容量 样本中所含数据(如测定值)的个数称为样本容量,用 n 表示。 3.算术平均值(前已讲) 4.中位数(M) 中位数(M)是指将一组测定值按一定大小顺序排列时的中间项的数值。 5.差方和 测定值对平均值偏差的平方的加和叫差方和。即

石河子大学化学化工学院分析化学教案 堂方和一密 6.方差(表征随机变量分布的离散程度) 个别测定值与平均值的偏差的平方和除以测定次数(n-1)得方差。 .三6-沙 7-1 7.标准偏差(前己介绍) (区-4 S=1 8-1 8.相对标准偏差(前己介绍) 相对标准偏热。=三x10。 9.平均偏差ā和相对平均偏差 a.+,+.+则空k- 相对平均偏差=x100% 10.极差R(全距) 在一组数据中最大值与最小值之差称为极差(又叫全距或范围误差),用R表示。即 R=X大·X 11.频数 将平行测定次数足够多的数据划分为若干组,落入每一个组内的数据个数叫该组数据的 频数 12.相对频数 频数与所测数据总个数(样本容量)之比值,叫相对频数(即频率或概率)。 13.概率密度 各组数据的相对频数(概率)除以组距就是概率密度。 组距就是最大值与最小值之差除以组数。 二、测定值的频数分布
石河子大学化学化工学院-分析化学教案 8 6.方差 (表征随机变量分布的离散程度) 个别测定值与平均值的偏差的平方和除以测定次数(n-1)得方差。 7.标准偏差(前已介绍) 8.相对标准偏差(前已介绍) 9.平均偏差 和相对平均偏差 10.极差 R(全距) 在一组数据中最大值与最小值之差称为极差(又叫全距或范围误差),用 R 表示。即 R = X 最大 - X 最小 11.频数 将平行测定次数足够多的数据划分为若干组,落入每一个组内的数据个数叫该组数据的 频数。 12.相对频数 频数与所测数据总个数(样本容量)之比值,叫相对频数(即频率或概率)。 13.概率密度 各组数据的相对频数(概率)除以组距就是概率密度。 组距就是最大值与最小值之差除以组数。 二、测定值的频数分布 d
石河子大学化学化工学院分析化学教案 ()算出极差R 例如,测定镍合金试样中镍的质量分数(%),即百分含量,在相同条件下共测定90 249表所示。 R=X大-X0本=1.74-1.49=0.25 白确定组数和组 组数的确定视样本容量而定,容量大时分成10-20组,容量小时(<50)分成57组。 在该测定中分成9组。 确定组数之后 就要求组距 组距:最大值减最小值用组数除即得组距(即极差除以组数)。该例的组距为: 组距.最大值-最小值.174-142.0.03 0 0 白快具同型夫黄香一个相的个意高性 频数与样本总数(即样本容量总数)之比(称为相对频数:若以%表示,则称频率)。然后 将组值范围、颜数和相对频数列入表中,即可得频数分布表(见四师P49表)。 四绘直方图 若以组界值为横坐标,相对频数(频率)为纵坐标作图,可得相对频数分布直方图(四 师P49)。相对频数直方图上长方形的总面积为1。 在全部测定数据中,位于中间数值1.57-1.69之间的数据多一些,在其它范围的数据少 一些,小至1.49,大至1.74附近的数据就更少。也就是说,测定值具有明显的集中趋势。 测定数据的这种既分散又集中的特性,就是其内在规律性的表现。 三、随机误差的正态分布 1.正态分布N( 、0 随机误差的正态分布性质,用高斯分布米描述,它的数学表达式为: e 1 y=f(x)= (1) 图1平均值相同,精密度不同 图2精密度相同,平均值不同 从(1)式高斯分布的数学表达式和正态分布曲线可以看到平均值μ和总体标准偏差· 是正态分布的两个基本参数。给定了μ和·,正态分布曲线就完全确定了。 不管总体标准差·为何值,分布曲线和横坐标之间所夹的总面积代表各种大小偏差的样 9
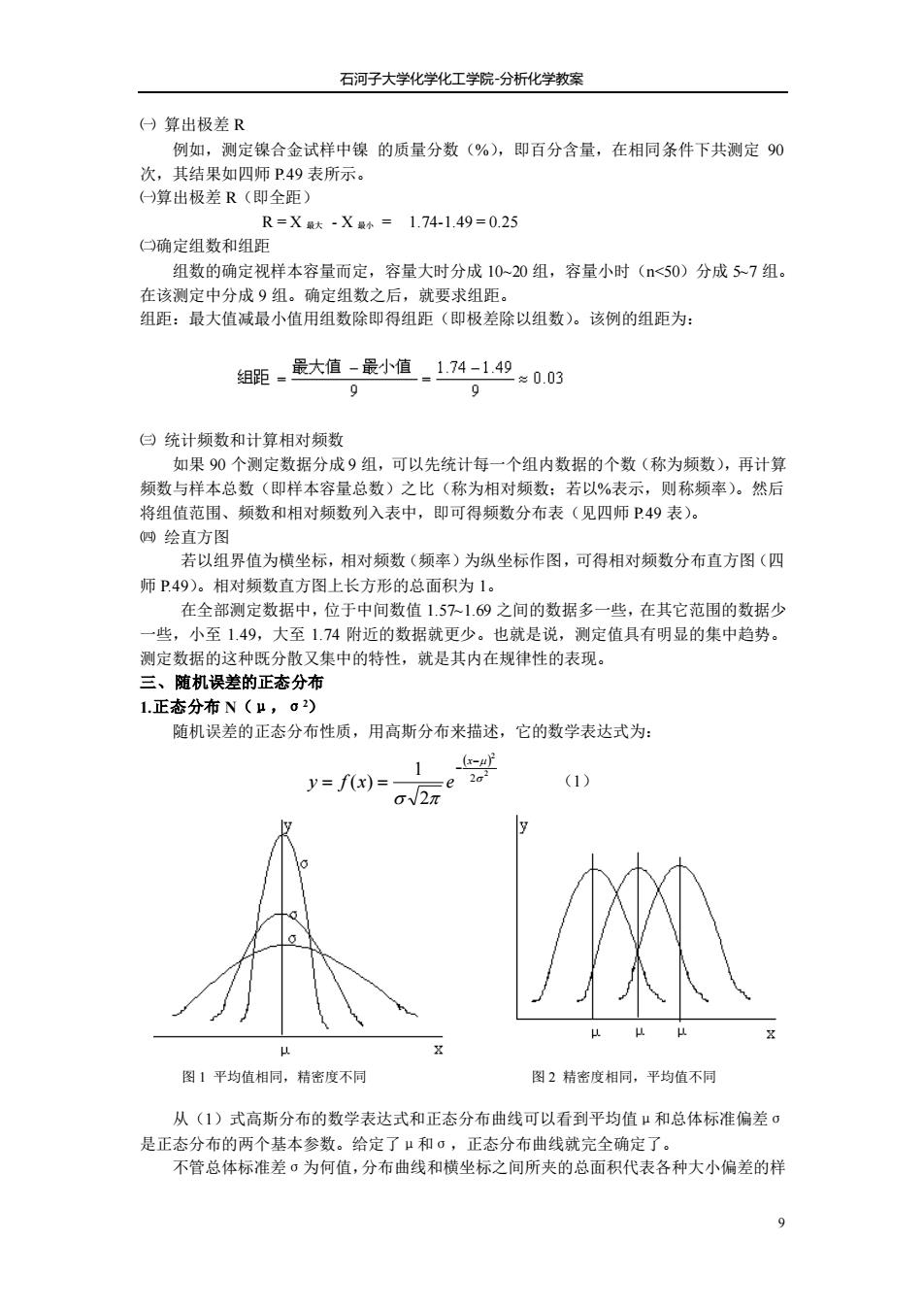
石河子大学化学化工学院-分析化学教案 9 ㈠ 算出极差 R 例如,测定镍合金试样中镍 的质量分数(%),即百分含量,在相同条件下共测定 90 次,其结果如四师 P.49 表所示。 ㈠算出极差 R(即全距) R = X 最大 - X 最小 = 1.74-1.49 = 0.25 ㈡确定组数和组距 组数的确定视样本容量而定,容量大时分成 10~20 组,容量小时(n<50)分成 5~7 组。 在该测定中分成 9 组。确定组数之后,就要求组距。 组距:最大值减最小值用组数除即得组距(即极差除以组数)。该例的组距为: ㈢ 统计频数和计算相对频数 如果 90 个测定数据分成 9 组,可以先统计每一个组内数据的个数(称为频数),再计算 频数与样本总数(即样本容量总数)之比(称为相对频数;若以%表示,则称频率)。然后 将组值范围、频数和相对频数列入表中,即可得频数分布表(见四师 P.49 表)。 ㈣ 绘直方图 若以组界值为横坐标,相对频数(频率)为纵坐标作图,可得相对频数分布直方图(四 师 P.49)。相对频数直方图上长方形的总面积为 1。 在全部测定数据中,位于中间数值 1.57~1.69 之间的数据多一些,在其它范围的数据少 一些,小至 1.49,大至 1.74 附近的数据就更少。也就是说,测定值具有明显的集中趋势。 测定数据的这种既分散又集中的特性,就是其内在规律性的表现。 三、随机误差的正态分布 1.正态分布 N(μ,σ2) 随机误差的正态分布性质,用高斯分布来描述,它的数学表达式为: ( ) 2 2 2 2 1 ( ) − − = = x y f x e (1) 从(1)式高斯分布的数学表达式和正态分布曲线可以看到平均值μ和总体标准偏差σ 是正态分布的两个基本参数。给定了μ和σ,正态分布曲线就完全确定了。 不管总体标准差σ为何值,分布曲线和横坐标之间所夹的总面积代表各种大小偏差的样 图 1 平均值相同,精密度不同 图 2 精密度相同,平均值不同

石河子大学化学化工学院分析化学教案 本值出现概率的总和,这就是概率密度函数在.∞x<∞区间的积分值,其值为1,即 瓶率Rx网=。八h=面积=。 2.标准正态分布曲线NO,) 高斯正态分布的数学表达式(1式)中,X、“、都是变量,计算不便。为此常采用 变量转换的办法,将平均值的偏差(xμ)以。为单位,即令 划= X-4 则xμ以任何值出现时,就可由其相当于u个。而得出。 1:有一系列Fe的分析数据,μ=53.78%Fe,o=0.20%,计算x=53.58%Fe时的u 解 u=X-45358-5378 -1.0 G 0.20 这就是说,当一次测定值xX=53.58%时,偏离总体平均值为一个标准差,即一个u单位。 例2:某化学课程最终考试,平均成绩μ=75分,总体标准偏差0=10分,计算x=100分时 的u值。 解 4=X-业-100-75=25 10 即在此考试中,得满分的将以2.5个标准偏差出现。 将上式(所令u式)代入高斯数学表达式,得 V分ew 1 y=f(u)=- 若0=1,1=0,则 y=- 1e2=1e V2
石河子大学化学化工学院-分析化学教案 10 本值出现概率的总和,这就是概率密度函数在- ∞<x<∞区间的积分值,其值为 1,即 2. 标准正态分布曲线 N(0,1) 高斯正态分布的数学表达式(1 式)中,x、μ、σ都是变量,计算不便。为此常采用 变量转换的办法,将平均值的偏差(x-μ)以σ为单位,即令 则 x-μ以任何值出现时,就可由其相当于 u 个σ而得出。 例 1:有一系列 Fe 的分析数据,μ=53.78%Fe,σ=0.20%,计算 x=53.58%Fe 时的 u。 解: 这就是说,当一次测定值 x=53.58% 时,偏离总体平均值为一个标准差,即一个 u 单位。 例 2:某化学课程最终考试,平均成绩μ=75 分,总体标准偏差σ=10 分,计算 x=100 分时 的 u 值。 解: 即在此考试中,得满分的将以 2.5 个标准偏差出现。 将上式(所令 u 式)代入高斯数学表达式,得

石河子大学化学化工学院分析化学教案 经过变量转换后,平均值为山,总体标准偏差为σ的正态分布曲线为:平均值μ=0, 总体标准偏差=1的正态分布曲线,这种特殊的正态分布曲线称为标准正态分布曲线,用 N(0 1 表示 (四师P52图3-5 3.标准正态分布概率密度函数积分表(会用) 假定测定值出现在=±∞这样的无限范围内,则其出现的几率就等于100%。 如果测定值出现在u∞到0或u由0到+∞之间,则在该范围内出现的几率分别为 50%。 u和面积的关系列于四师P54表31 例3:某数值X落在平均值(指总体平均值)的2个标准偏差(。)以内的概率是多少?落 在平均值的3个标准偏差以内的概率是多少? 解:查四师P.54表31,=2时的面积为0.4773,于是出现的概率为: P=2x0.473×100%=95.59% 1 当u=3时,面积为0.4987,于是出现的概率为: p-2x0.4987 x100%=99.7% 四师P54例3-3,34(略) 讨论: ·1.假如对Fz0:进行了多次测定。F0的平均含量μ为11.04%,0为0.03%, 试计算F2O方含量落在2个标准偏差以内的几率。 ·解:查表u2时,面积为0.4773,于是出现的概率为: P 2×0.4773×100%=95.5% ·2.已知某试样中含C0的标准值为1.75%,标准偏差。-0.10%,设测量时无系统误 差,求分析结果落在1.75%±0.15%范围内的概率。 ·解: M=-A_k-175%Q15g =1.5 0.10%0.10% ·查正态分布概率积分表,=1.5时,概率为0.4554 ·分析结果落在1.75%±0.15%范围内的概率应为2×0.4554-86.6%。 ·3.已知某试样中含C0的标准值为1.75%,标准偏差0=0.10%,设测量时无系统 误差,求分析结果大于2.00%的概率。 ·解:此屈单侧检验的问题。 M-k-4_200%-1754-25 6 0Q.10% ·查积分表,=2.5时,概率为0.4938,整个正态分布曲线右侧的概率为1/2,即0.5000
石河子大学化学化工学院-分析化学教案 11 经过变量转换后,平均值为μ,总体标准偏差为σ的正态分布曲线为:平均值μ=0, 总体标准偏差σ=1 的正态分布曲线,这种特殊的正态分布曲线称为标准正态分布曲线,用 N(0,1)表示。(四师 P.52 图 3-5)。 3.标准正态分布概率密度函数积分表(会用) 假定测定值出现在 u=±∞这样的无限范围内,则其出现的几率就等于 100%。 如果测定值出现在 u= -∞到 u=0 或 u 由 0 到+∞之间,则在该范围内出现的几率分别为 50%。 u 和面积的关系列于四师 P.54 表 3-1。 例 3:某数值 x 落在平均值(指总体平均值)的 2 个标准偏差(σ)以内的概率是多少?落 在平均值的 3 个标准偏差以内的概率是多少? 解:查四师 P.54 表 3-1,u=2 时的面积为 0.4773,于是出现的概率为: 当 u=3 时,面积为 0.4987,于是出现的概率为: 四师 P.54 例 3-3,3-4 (略) 讨论: • 1. 假如对 Fe2O3 进行了多次测定。Fe2O3 的平均含量μ为 11.04%,σ为 0.03%, • 试计算 Fe2O3 含量落在 2 个标准偏差以内的几率。 • 解:查表 u=2 时,面积为 0.4773,于是出现的概率为: • • 2. 已知某试样中含 Co 的标准值为 1.75%,标准偏差σ=0.10%,设测量时无系统误 • 差,求分析结果落在 1.75%±0.15%范围内的概率。 • 解: • 查正态分布概率积分表,u=1.5 时,概率为 0.4554。 • 分析结果落在 1.75%±0.15%范围内的概率应为 2×0.4554=86.6%。 • 3. 已知某试样中含 Co 的标准值为 1.75%,标准偏差σ=0.10%,设测量时无系统 • 误差,求分析结果大于 2.00%的概率。 • 解:此属单侧检验的问题。 • 查积分表,u=2.5 时,概率为 0.4938,整个正态分布曲线右侧的概率为 1/2,即 0.5000, 100% 95.5% 1 2 0.4773 P = = 1.5 0.10% 0.15% 0.10% x 1.75% σ x μ u = = − = − = 2.5 0.10% 2.00% 1.75% σ x μ u = − = − =

石河子大学化学化工学院分析化学教案 故落在大于2.00%的概率为: 0.5000-0.4938=-0.62 4.求平均值u-0.60至μ+0.6o区间内的概率 ·解:由题意知:u=±0.6 查正态分布概率积分表,=0.6时,积分面积为0.2258,此为双侧分布。 ·故概率为:02258×2-45.16% ·5.对某试样中铁含量量进行了130次分析,分析结果符合正态分布N(55.20%, 20%),求分析结果大于55.60%可能出现的次数。 解 M=x-4_5版606-5改204-20 0.20% ·查概率积分表,u-2.0时,概率为0.4773整个正态分布曲线右侧的概率为0.5000, 结果大于55.60%之概率应为 0.5000-0.4773=0.0227 ·故 130×2.27%≈3(次) ·作业:P7214、15、16、17、18题 §3-4有限测定数据的统计处理 一、置信度与“的置信区间 真值落在某一指定范围内的概率就叫置信概率(或叫置信度,置信水平),这个范围就叫做 置信区间。 ()置信度 假设分析某钢样中的含磷量,四次平行测定的平均值为0.0087%。已知0=0.0022%,如 果将分析结果报告为: u=x±ug n 4=0.0087%±1x00022%-0.00876±0.0019% 4 或写成 {-)(+】0 单侧分布的概率为: 0.683=0.3415
石河子大学化学化工学院-分析化学教案 12 故落在大于 2.00%的概率为: • 0.5000-0.4938=0.62% • 4. 求平均值μ-0.6σ至μ+0.6σ区间内的概率。 • 解:由题意知:u=±0.6 • 查正态分布概率积分表,u=0.6 时,积分面积为 0.2258,此为双侧分布。 • 故概率为:0.2258×2=45.16% • 5. 对某试样中铁含量量进行了 130 次分析,分析结果符合正态分布 N(55.20%, • 0.20%),求分析结果大于 55.60%可能出现的次数。 • 解: • 查概率积分表,u=2.0 时,概率为 0.4773,整个正态分布曲线右侧的概率为 0.5000, 结果大于 55.60%之概率应为 • 0.5000-0.4773=0.0227 • 故 130×2.27%≈3(次) • • 作业:P.72 14、15、16、17、18 题 §3-4 有限测定数据的统计处理 一、置信度与μ的置信区间 真值落在某一指定范围内的概率就叫置信概率(或叫置信度,置信水平), 这个范围就叫做 置信区间。 ㈠置信度 假设分析某钢样中的含磷量,四次平行测定的平均值为 0.0087%。已知σ=0.0022%,如 果将分析结果报告为: 或写成: 单侧分布的概率为: 2.0 0.20% 55.60% 55.20% σ x μ u = − = − =