
第七章特征变换 966 特征选择 口从D个原始特征中,选择其中的d个特征。保持了 原有特征的物理含义 特征变换 对D个原始特征进行一定的数学变换,得到d组新 特征,往往不具有原始特征对应的物理含义
第七章 特征变换 特征选择 从D个原始特征中,选择其中的d个特征。保持了 原有特征的物理含义 特征变换 对D个原始特征进行一定的数学变换,得到d组新 特征,往往不具有原始特征对应的物理含义

/96 天=(x,x2,…,xn)→ =(,2,…,ya),d≤n 变换)=W”龙 原始特征 二次特征 W=Wx为特征提取矩阵或变换矩阵
变换 T y W x W Wnd为特征提取矩阵或变换矩阵 1 2 ( , , , )T n x x x x 1 2 ( , , , ) , T d y y y y d n 原始特征 二次特征

纷 /96 主成分分析PCA)
主成分分析(PCA)

/96 在模式识别中,一个常见的问题就是特征 选择或特征提取,理论上我们要选择与原始数 据空间相同的维数。但是,为了简化计算,设 计一种变换使得数据集由维数较少的“有效” 特征来表示。 找出数据中最“主要”的元素和结构,去 除噪音和冗余,将原有的复杂数据降维,揭示 隐藏在复杂数据背后的简单结构
在模式识别中,一个常见的问题就是特征 选择或特征提取,理论上我们要选择与原始数 据空间相同的维数。但是,为了简化计算,设 计一种变换使得数据集由维数较少的“有效” 特征来表示。 找出数据中最“主要”的元素和结构,去 除噪音和冗余,将原有的复杂数据降维,揭示 隐藏在复杂数据背后的简单结构
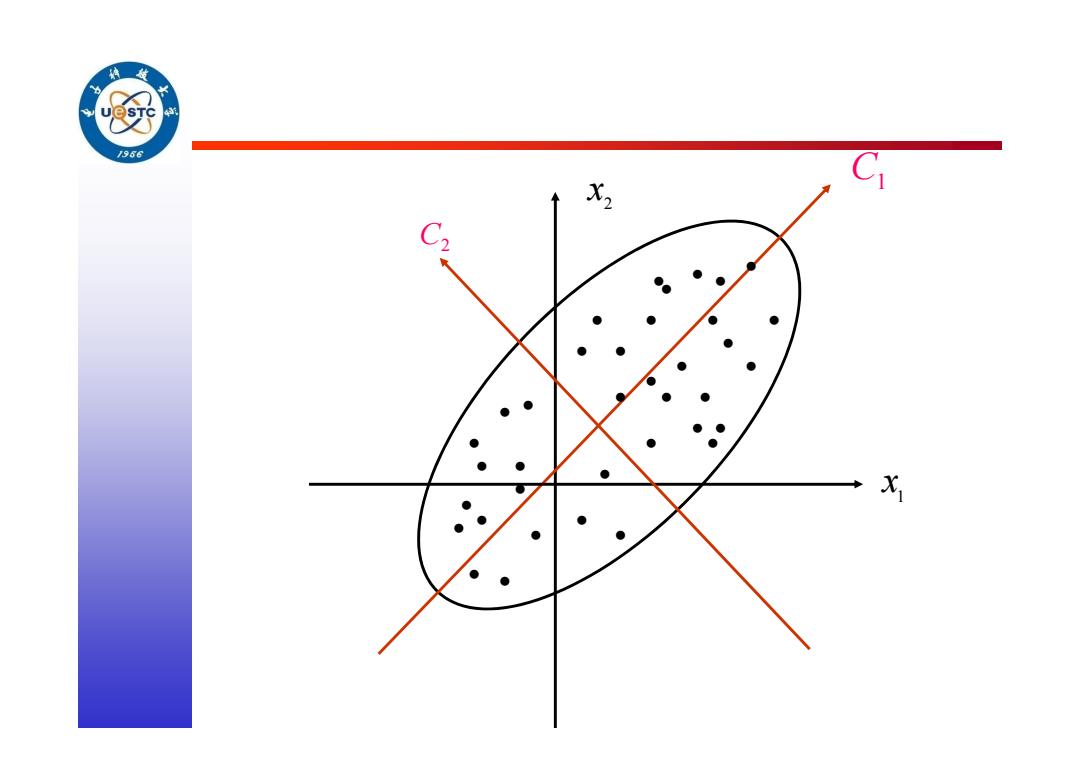
/956 X2 C S ● ● ● ● ● ● X
• 2 x 1 x C1 C2 • • • •••• • • • • • • • • • • • • • • • • • • • • • • • • • • • • •

J966 PCA的优点是简单,而且无参数限制,可以方便 的应用与各个场合。 因此应用极其广泛,从神经科学到计算机图形学 都有它的用武之地。被誉为应用线性代数最有价 值的结果之一
PCA的优点是简单,而且无参数限制,可以方便 的应用与各个场合。 因此应用极其广泛,从神经科学到计算机图形学 都有它的用武之地。被誉为应用线性代数最有价 值的结果之一

966 在PCA中,我们感兴趣的是找到一个从原d维输 入空间到新的k维空间的具有最小信息损失的 映射。 X在方向w上的投影为: z=w"x
在PCA中,我们感兴趣的是找到一个从原d维输 入空间到新的k维空间的具有最小信息损失的 映射。 X在方向w上的投影为:

主成分的定义及导出 /966 设x=(x,2,,xn)/为一个n维随机向量,Co(x)=∑ 主成分z,是这样的,样本投影到21上之后被广泛散布, 使得样本之间的差别变得最明显,即最大化方差。 设31=wx 希望在约束条件 w=1下寻求向量%, 使 var(3)=w∑w最大化
主成分的定义及导出 设 为一个n维随机向量, 主成分 是这样的,样本投影到 上之后被广泛散布, 使得样本之间的差别变得最明显,即最大化方差。 设 希望在约束条件 下寻求向量 , 使 最大化 1 2 ( , ,..., )T n x x x x Cov x( ) 1 z 1z 1 1 T z w x 1 w 1 w1 var 1 1 1 T z w w

J966 写成拉格朗日问题 maxw∑w,-(ww,-1) (1) 91 现在关于州求导并令其等于0,得到 2∑W-2aw=0→∑w=Q4 如果%是∑的特征向量,是对应的 特征值,则上式是成立的
写成拉格朗日问题 现在关于 求导并令其等于0,得到 如果 是 的特征向量, 是对应的 特征值,则上式是成立的 max ( 1) (1) 1 1 1 1 1 w w w w T T w w1 1 1 1 1 2 w 2w 0 w w w1

/96 同时我们还得到 w∑W=cww=C 为了使方差最大,选择具有最大特征值 的特征向量,因此,第一个主成分 是输入样本协方差阵的具有最大特征值 对应的特征向量
同时我们还得到 为了使方差最大,选择具有最大特征值 的特征向量 ,因此,第一个主成分 是输入样本协方差阵的具有最大特征值 对应的特征向量