
SMEE 机械与电气工程学院 School of Machanical and Elcetrical Engineering 第五章滤波器 一 理想滤波器 二、常见滤波算法 三、高通/低通滤波器 四、带通/带阻滤波器 五、选频网络 机越与电气工程学院
机械与电气工程学院 School of Machanical and Elcetrical Engineering 第五章 滤波器 一、理想滤波器 二、常见滤波算法 三、高通/低通滤波器 四、带通/带阻滤波器 五、选频网络
机械与电气工程学院 School of Machanical and Elcetrical Engineering 滤波器的本质: 选频网络一 让信号中特定频率成份通过,抑制或衰减其它频率成份。 因此,频率响应是其重要特性。 低通、高通、带通、带阻滤波器 RC、LC、晶振滤波器 滤波器的分类 有源滤波器、无源滤波器 模拟滤波器、数字滤波器 机越与电气工程学院
机械与电气工程学院 School of Machanical and Elcetrical Engineering 滤波器的本质: 选频网络 —— 让信号中特定频率成份通过,抑制或衰减其它频率成份。 因此,频率响应是其重要特性。 低通、高通、带通、带阻滤波器 RC、LC、晶振滤波器 有源滤波器、无源滤波器 模拟滤波器、数字滤波器 滤波器的分类

SMEE 机械与电气工程学院 School of Machanical and Elcetrical Engineering 一、 理想滤波器 理想滤波器是将某些特性理想化的一个理想化的滤波网络, 在物理上不可能实现。理想滤波器的研究有助于理解滤波器的 传输特性,导出的结论可作为实际滤波器传输特性分析的基础。 理想滤波器的特性:在所需的通频带内幅频特性为常数, 在通带外幅频特性值应为零;相频特性为通过原点的直线。 H() Ao 0 0 (a) (b) 理想滤波器的频率特性 机越与电气工程学院
机械与电气工程学院 School of Machanical and Elcetrical Engineering 理想滤波器是将某些特性理想化的一个理想化的滤波网络, 在物理上不可能实现。理想滤波器的研究有助于理解滤波器的 传输特性,导出的结论可作为实际滤波器传输特性分析的基础。 理想滤波器的特性:在所需的通频带内幅频特性为常数, 在通带外幅频特性值应为零;相频特性为通过原点的直线。 一、理想滤波器 理想滤波器的频率特性
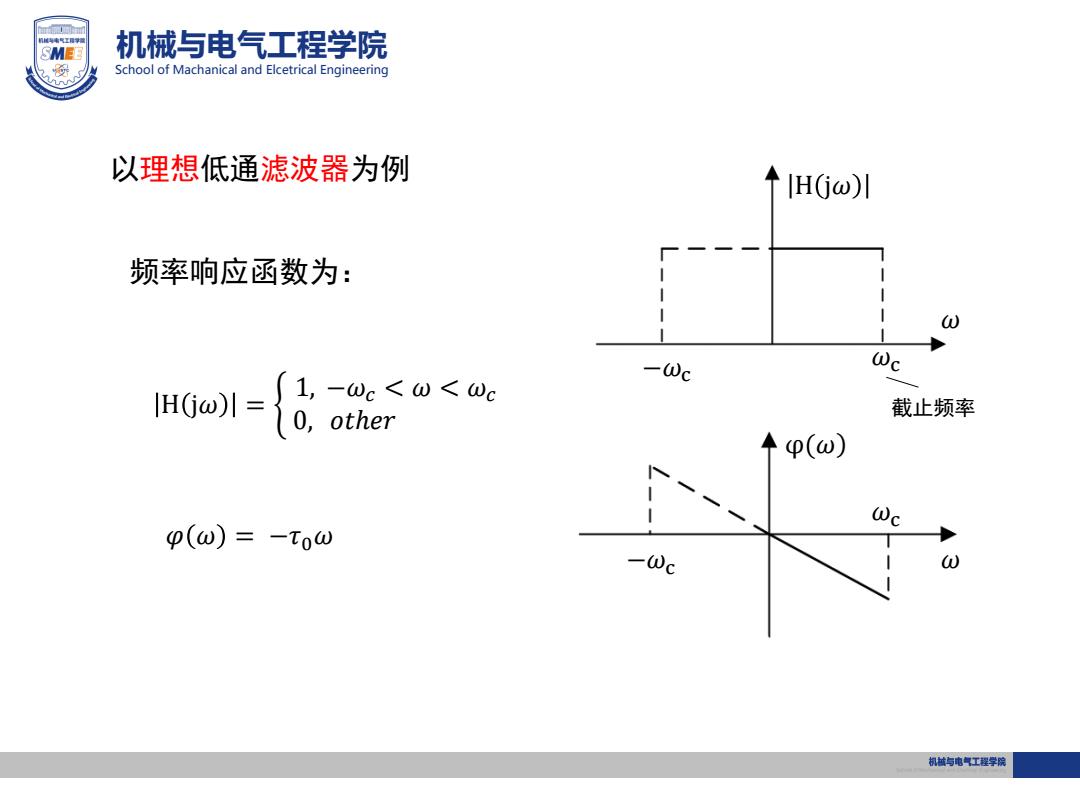
SMEE 机械与电气工程学院 School of Machanical and Elcetrical Engineering 以理想低通滤波器为例 JHGj@)l 频率响应函数为: 一c Wc HGo1={0. 1, -ωc<w<ωc other 截止频率 个p(ω) Wc p(ω)=-t0ω W 机越与电气工程学院
机械与电气工程学院 School of Machanical and Elcetrical Engineering −𝜔 𝜔c c 𝜔 以理想低通滤波器为例 H j𝜔 H j𝜔 = 1, −𝜔𝑐 < 𝜔 < 𝜔𝑐 0, 𝑜𝑡ℎ𝑒𝑟 截止频率 频率响应函数为: 𝜑 𝜔 = −𝜏0𝜔 φ(𝜔 −𝜔c 𝜔c 𝜔
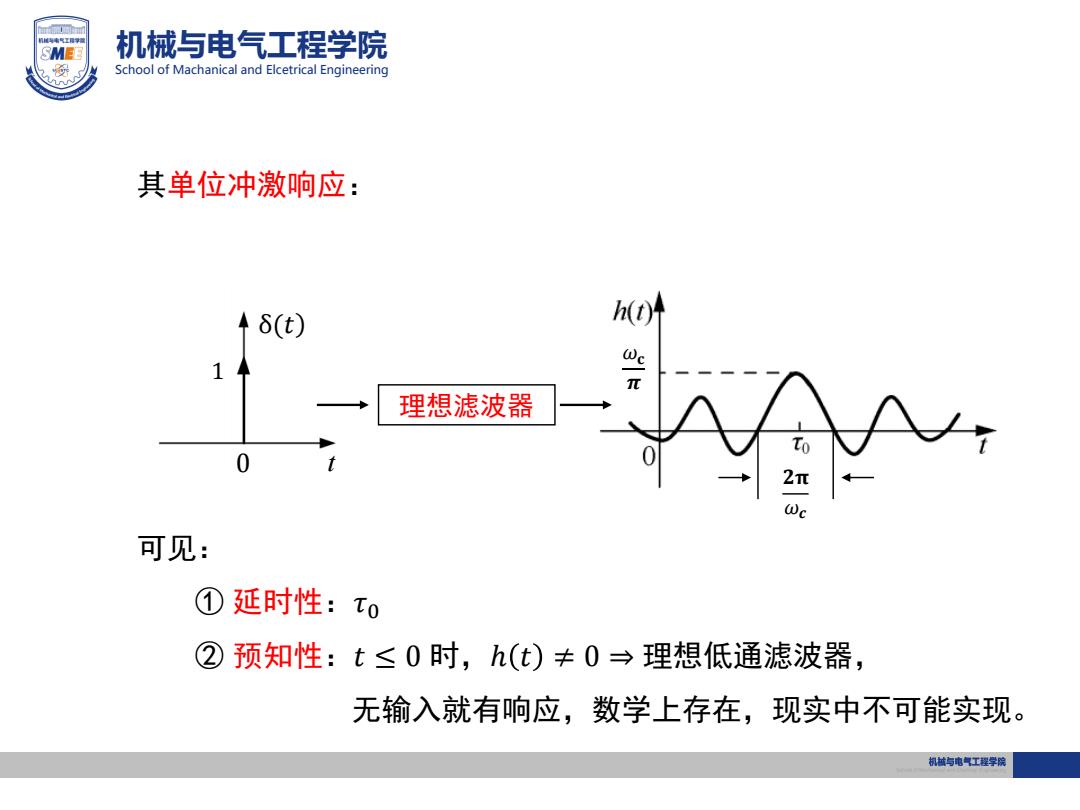
SMEE 机械与电气工程学院 School of Machanical and Elcetrical Engineering 其单位冲激响应: 6(t) h(t) 理想滤波器 To 0 2π 可见: ① 延时性:To ②预知性:t≤0时,h(t)≠0→理想低通滤波器, 无输入就有响应,数学上存在,现实中不可能实现。 机械与电气工程学院
机械与电气工程学院 School of Machanical and Elcetrical Engineering 其单位冲激响应: δ(𝑡 1 t 𝜔𝐜 𝝅 𝟐𝛑 𝜔𝒄 可见: ① 延时性:𝜏0 ② 预知性:𝑡 ≤ 0 时,ℎ 𝑡 ≠ 0 ⇒ 理想低通滤波器, 无输入就有响应,数学上存在,现实中不可能实现。 理想滤波器 0

机械与电气工程学院 School of Machanical and Elcetrical Engineering 实际低通滤波器 实际滤波器的频率响应特性是不可能直角锐变,也不可能在有限 频率上完全截止,将延伸到f引→∞。对通频带以外的频率成分只能 极大地衰减,却无法完全阻止,只能按“最佳逼近特性”设计构建。 4HGω)川 通带 过渡带 阻带 Wc ①满足幅频特性→巴特沃兹、切比雪夫滤波器 ②满足相频特性→贝塞尔滤波器 机越与电气工程学院
机械与电气工程学院 School of Machanical and Elcetrical Engineering 实际滤波器的频率响应特性是不可能直角锐变,也不可能在有限 频率上完全截止,将延伸到 𝑓 → ∞ 。对通频带以外的频率成分只能 极大地衰减,却无法完全阻止,只能按“最佳逼近特性”设计构建。 实际低通滤波器 ① 满足幅频特性 → 巴特沃兹、切比雪夫滤波器 ② 满足相频特性 → 贝塞尔滤波器
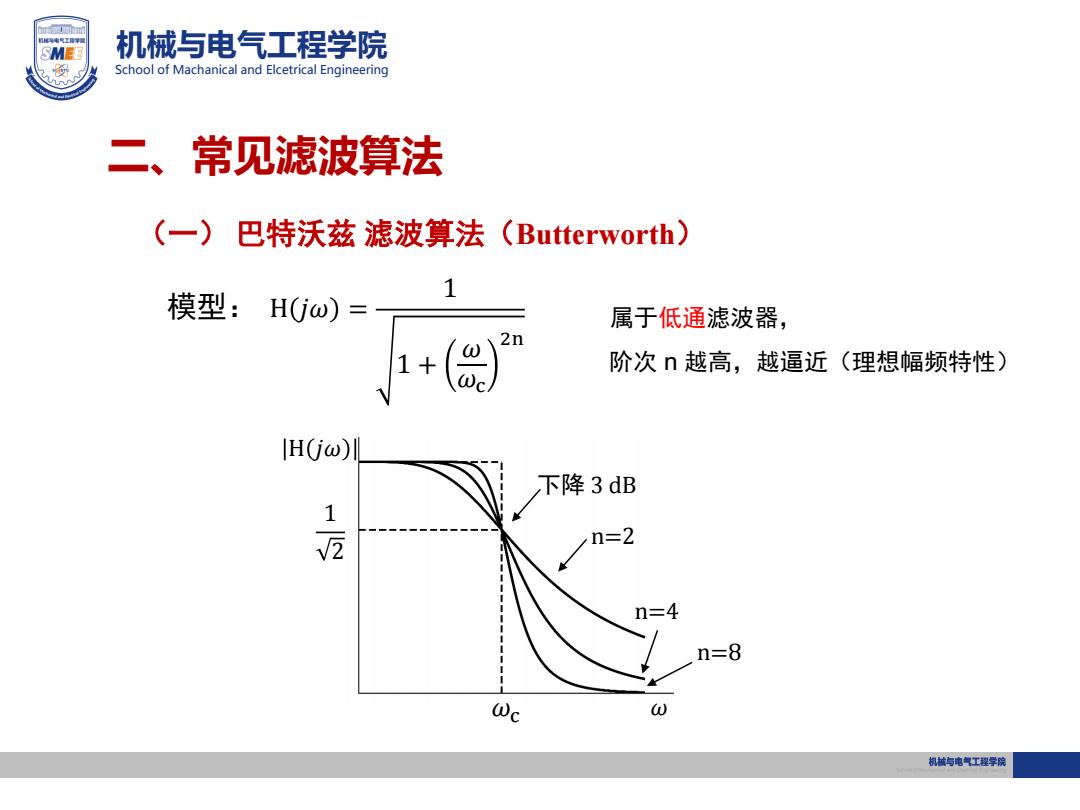
SMEE 机械与电气工程学院 School of Machanical and Elcetrical Engineering 二、常见滤波算法 (一)巴特沃兹滤波算法 (Butterworth) 1 模型:Hjw)= 属于低通滤波器, 2n 1+ 阶次n越高,越逼近(理想幅频特性) lH(j@)‖ 下降3dB V n=2 n=4 n=8 Wc 机与电气工程学院
机械与电气工程学院 School of Machanical and Elcetrical Engineering (一) 巴特沃兹 滤波算法(Butterworth) H 𝑗𝜔 = 1 1 + 𝜔 𝜔c 2n 属于低通滤波器, 阶次 n 越高,越逼近(理想幅频特性) H 𝑗𝜔 1 2 n=2 n=4 n=8 𝜔 下降 3 dB 二、常见滤波算法 𝜔c 模型:
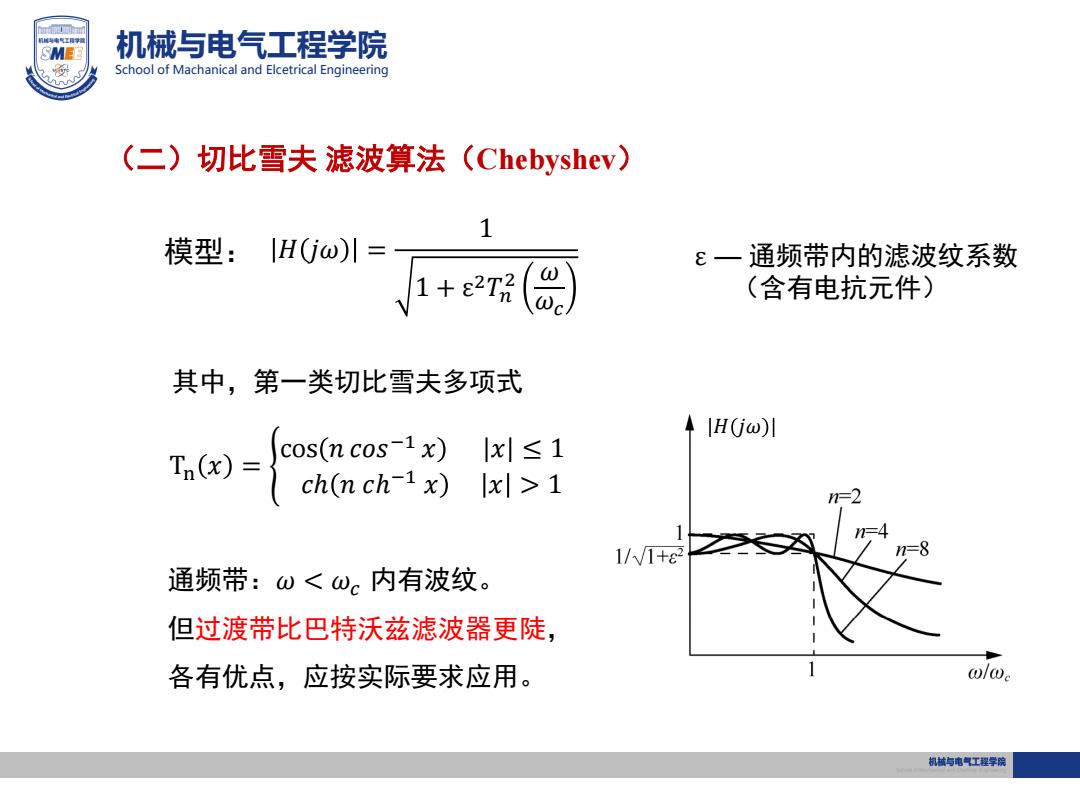
SMEE 机械与电气工程学院 School of Machanical and Elcetrical Engineering (二)切比雪夫滤波算法(Chebyshev) 1 模型:IHGω)川= ε一通频带内的滤波纹系数 1+e2r(品) (含有电抗元件) 其中,第一类切比雪夫多项式 H(jo) cos(n cos-1x) |x|≤1 ch(n ch-1x)Ix >1 =2 1//1+e 23☒ 通频带:ω<ωc内有波纹。 但过渡带比巴特沃兹滤波器更陡, 各有优点,应按实际要求应用。 ω/0c 机越与电气工程学院
机械与电气工程学院 School of Machanical and Elcetrical Engineering (二)切比雪夫 滤波算法(Chebyshev) 模型: 𝐻 𝑗𝜔 = 1 1 + ε 2𝑇𝑛 2 𝜔 𝜔𝑐 ε — 通频带内的滤波纹系数 (含有电抗元件) 𝐻 𝑗𝜔 Tn 𝑥 = cos 𝑛 𝑐𝑜𝑠−1 𝑥 𝑥 ≤ 1 𝑐ℎ 𝑛 𝑐ℎ −1 𝑥 𝑥 > 1 其中,第一类切比雪夫多项式 通频带:𝜔 < 𝜔𝑐 内有波纹。 但过渡带比巴特沃兹滤波器更陡, 各有优点,应按实际要求应用

SMEE 机械与电气工程学院 School of Machanical and Elcetrical Engineering (三)贝塞尔滤波算法(Bessel) p(ω) ω ⊙0 满足相频最佳逼近特性, 贝塞尔n=2 具有较好的相频特性, 贝塞尔n=4 但幅频特性欠佳。 切比雪夫n=4 巴特沃滋n=4 机械与电气工程学院
机械与电气工程学院 School of Machanical and Elcetrical Engineering 𝜑(𝜔 𝜔 𝜔0 贝塞尔 n = 2 贝塞尔 n = 4 切比雪夫 n = 4 巴特沃兹 n = 4 满足相频最佳逼近特性, 具有较好的相频特性, 但幅频特性欠佳。 (三)贝塞尔 滤波算法(Bessel)
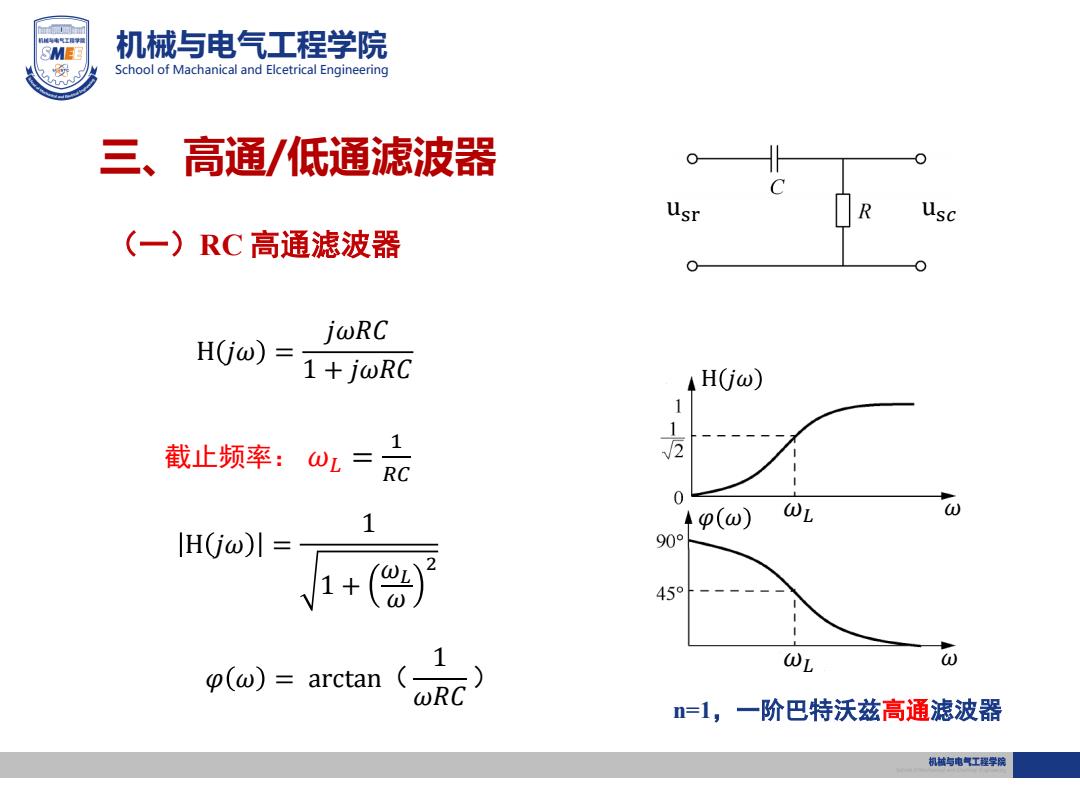
SMEE 机械与电气工程学院 School of Machanical and Elcetrical Engineering 三、高通/低通滤波器 usc (一)RC高通滤波器 jωRC HGjω)= 1+jωRC 4HGω) 1 截止频率:ωL=R 2 0 1 4p(ω) WL U IHG0ω)1= 90° 、1+() 45o p(ω)=arctan( L ωRC =1,一阶巴特沃兹高通滤波器 机越与电气工程学院
机械与电气工程学院 School of Machanical and Elcetrical Engineering H 𝑗𝜔 = 𝑗𝜔𝑅𝐶 1 + 𝑗𝜔𝑅𝐶 截止频率: 𝜔𝐿 = 1 𝑅𝐶 H 𝑗𝜔 = 1 1 + 𝜔𝐿 𝜔 2 𝜔𝐿 usr us𝑐 (一)RC 高通滤波器 𝜑 𝜔 = arctan( 1 𝜔𝑅𝐶 ) H 𝑗𝜔 𝜑 𝜔 𝜔𝐿 𝜔 𝜔 三、高通/低通滤波器 n=1,一阶巴特沃兹高通滤波器