
机械与电气工程学院 School of Machanical and Elcetrical Engineering 第二章信号的数学分析 一、信号的时域特征值 二、信号的幅值域特征值 三、信号的相关域特征值 四、信号的频率域特征值 五、常见信号形式 六、信号的算法规则 机越与电气工程学院
机械与电气工程学院 School of Machanical and Elcetrical Engineering 第二章 信号的数学分析 一、信号的时域特征值 二、信号的幅值域特征值 三、信号的相关域特征值 四、信号的频率域特征值 五、常见信号形式 六、信号的算法规则

SME 机械与电气工程学院 网 School of Machanical and Elcetrical Engineering 信号的数学特征:动态信号的数学分析 本章思想: 建立信号的数学分析 信号的本质特性 信号的类型: 确定性信号:①周期信号、非周期信号。 ②能用明确的数学表达式或者通过实验能重复产生。 非确定性信号:随机信号(平稳信号、非平稳信号) 机越与电气工程学院
机械与电气工程学院 School of Machanical and Elcetrical Engineering 建立信号的数学分析 信号的数学特征:动态信号的数学分析 信号的本质特性 确定性信号:① 周期信号、非周期信号。 ② 能用明确的数学表达式或者通过实验能重复产生。 本章思想: 信号的类型: 非确定性信号:随机信号(平稳信号、非平稳信号)

SMEE 机械与电气工程学院 School of Machanical and Elcetrical Engineering 一、信号的时域特征值 (一)信号的均值 信号的均值描述了信号的趋势,反映了信号中的稳定分量。 均值通过数学期望的方法对信号的时间历程求其均值,是信号 对时间的均值,因此可以反映信号中静态量的大小。 k=E即x(ol-∫x)dt 说明: ① x(t):被测信号 T:观测时间长度 ② 上式适用于确定性信号和各态历经信号 机越与电气工程学院
机械与电气工程学院 School of Machanical and Elcetrical Engineering 一、信号的时域特征值 信号的均值描述了信号的趋势,反映了信号中的稳定分量。 均值通过数学期望的方法对信号的时间历程求其均值,是信号 对时间的均值,因此可以反映信号中静态量的大小。 𝜇𝑥 = 𝐸[𝑥(𝑡)] = 1 𝑇 0 𝑇 𝑥(𝑡) d𝑡 说明: ① 𝑥 𝑡 :被测信号 T:观测时间长度 ② 上式适用于确定性信号和各态历经信号 (一)信号的均值

SMEE 机械与电气工程学院 School of Machanical and Elcetrical Engineering (二)信号的均方根值(有效值) 说明: ① XTms的平方即是信号的平均功率Pav ② x,ms没有x(t)的物理量纲,没有“+”“_” ③均方值代表了信号的强度,如上信号均值为0,均方值不为0 机越与电气工程学院
机械与电气工程学院 School of Machanical and Elcetrical Engineering (二)信号的均方根值(有效值) 说明: ① 𝑥𝑟𝑚𝑠的平方即是信号的平均功率𝑃𝑎𝑣 ② 𝑥𝑟𝑚𝑠没有𝑥(𝑡)的物理量纲,没有 “+”“-” ③ 均方值代表了信号的强度,如上信号均值为0,均方值不为0 𝑥𝑟𝑚𝑠 = 1 𝑇 0 𝑇 𝑥 ) 2(𝑡 d𝑡

机械与电气工程学院 School of Machanical and Elcetrical Engineering (三)方差 方差定义为信号的取值与其均值之差的均方值,在数学上表 示为D[x(t)],在统计分析中简写为o?。 方差描述了信号的取值相对于其均值的偏离程度,用于了解 信号的波动情况。方差越小,表明信号取值越集中,上下波动越 小。对于平稳随机信号,由于其统计特性不随时间的变化而变化, 因此其方差也是常数,与时间无关。 机越与电气工程学院
机械与电气工程学院 School of Machanical and Elcetrical Engineering (三)方差 方差定义为信号的取值与其均值之差的均方值,在数学上表 示为𝐷[𝑥(𝑡)],在统计分析中简写为𝜎𝑥 2 。 方差描述了信号的取值相对于其均值的偏离程度,用于了解 信号的波动情况。方差越小,表明信号取值越集中,上下波动越 小。对于平稳随机信号,由于其统计特性不随时间的变化而变化, 因此其方差也是常数,与时间t无关
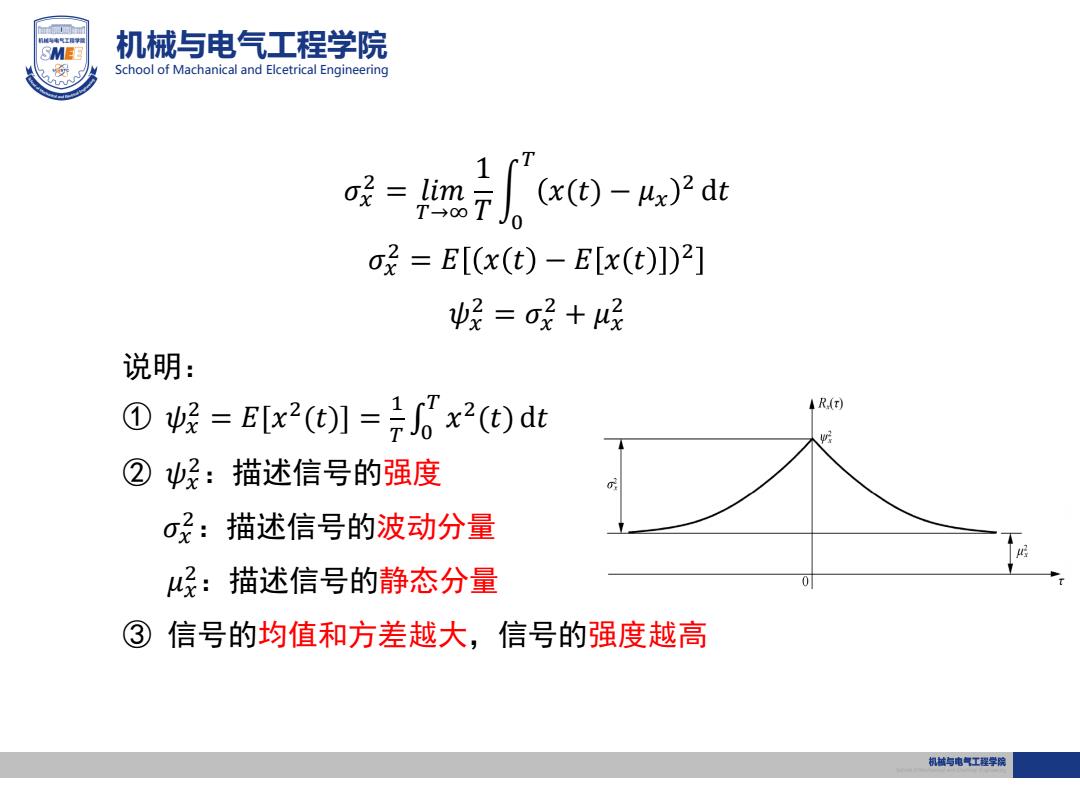
SMEE 机械与电气工程学院 School of Machanical and Elcetrical Engineering 吸=F(c四-Ax2dt o=E[(x(t)-E[x(t)])2] 经=经+呢 说明: ①候=E[x2(t]=0x2(t)dt 4R() ②ψ好:描述信号的强度 σ:描述信号的波动分量 ?:描述信号的静态分量 ③信号的均值和方差越大,信号的强度越高 机越与电气工程学院
机械与电气工程学院 School of Machanical and Elcetrical Engineering 𝜎𝑥 2 = 𝑙𝑖𝑚 𝑇→∞ 1 𝑇 0 𝑇 𝑥(𝑡) − 𝜇𝑥 2 d𝑡 𝜎𝑥 2 = 𝐸 𝑥 𝑡 − 𝐸 𝑥 𝑡 2 𝜓𝑥 2 = 𝜎𝑥 2 + 𝜇𝑥 2 说明: ① 𝜓𝑥 2 = 𝐸[𝑥 2 (𝑡)] = 1 𝑇 0 𝑇 𝑥 2 (𝑡) d𝑡 ② 𝜓𝑥 2:描述信号的强度 𝜎𝑥 2:描述信号的波动分量 𝜇𝑥 2:描述信号的静态分量 ③ 信号的均值和方差越大,信号的强度越高

机械与电气工程学院 School of Machanical and Elcetrical Engineering 二、信号的幅值域特征值 对于随机信号,其幅值的变化难以用具体的函数来描述,因 为它本身就毫无规律可言。然而对于大多数的平稳随机信号,可 以用统计的方法来描述信号取值的可能性,这就要用到概率统计 的数学方法。 (一)概率密度函数 设P[x≤x(t)≤x+△x]为信号x(t)的幅值在[x,x+△x]范围内取值 的概率,定义概率密度函数为 P[x≤x(t)≤X+△x] p(x)= lim △X→0 △X 机越与电气工程学院
机械与电气工程学院 School of Machanical and Elcetrical Engineering 二、信号的幅值域特征值 (一)概率密度函数 设𝑃[𝑥 ⩽ 𝑥(𝑡) ⩽ 𝑥 + Δ𝑥]为信号𝑥(𝑡)的幅值在 𝑥, 𝑥 + Δ𝑥 范围内取值 的概率,定义概率密度函数为 𝑝(𝑥) = 𝑙𝑖𝑚 Δ𝑥→0 𝑃[𝑥 ⩽ 𝑥(𝑡) ⩽ 𝑥 + Δ𝑥] Δ𝑥 对于随机信号,其幅值的变化难以用具体的函数来描述,因 为它本身就毫无规律可言。然而对于大多数的平稳随机信号,可 以用统计的方法来描述信号取值的可能性,这就要用到概率统计 的数学方法
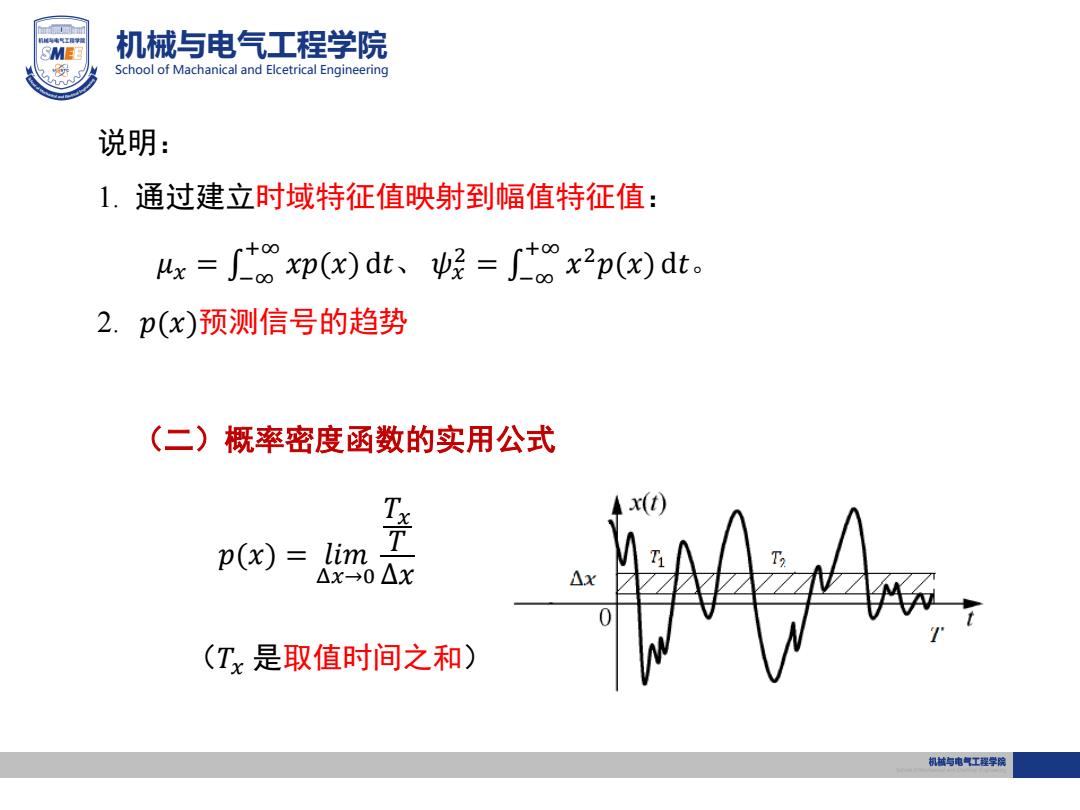
SMEE 机械与电气工程学院 School of Machanical and Elcetrical Engineering 说明: 1.通过建立时域特征值映射到幅值特征值: 4x=∫txp(x)dt、经=∫tox2p(x)dt。 2.p(x)预测信号的趋势 (二)概率密度函数的实用公式 lim 季 4x(t) p(x)= △X→0△X (Tx是取值时间之和) 机越与电气工程学院
机械与电气工程学院 School of Machanical and Elcetrical Engineering 说明: 1. 通过建立时域特征值映射到幅值特征值: 𝜇𝑥 = −∞ +∞ 𝑥𝑝(𝑥) d𝑡、 𝜓𝑥 2 = −∞ +∞ 𝑥 2𝑝(𝑥) d𝑡。 2. 𝑝(𝑥)预测信号的趋势 (二)概率密度函数的实用公式 𝑝(𝑥) = 𝑙𝑖𝑚 Δ𝑥→0 𝑇𝑥 𝑇 Δ𝑥 (𝑇𝑥 是取值时间之和)

机械与电气工程学院 School of Machanical and Elcetrical Engineering 三、信号的相关域特征值 (一)自相关函数 表征信号与其本身在时移τ后的关联程度,它描述了信号自身 变化的平稳性,即变化缓慢还是剧烈。 1.连续信号x(t)的自相关函数,其中τ为观测间隔: ()t 对于平稳随机信号,上式变为: Rx()=lim子∫x(t)x(t+t)p(x)dt T00 机越与电气工程学院
机械与电气工程学院 School of Machanical and Elcetrical Engineering 三、信号的相关域特征值 (一)自相关函数 表征信号与其本身在时移𝜏后的关联程度,它描述了信号自身 变化的平稳性,即变化缓慢还是剧烈。 1. 连续信号𝑥(𝑡)的自相关函数,其中𝜏为观测间隔: 𝑅𝑥(𝜏) = 𝑙𝑖𝑚 𝑇→∞ 1 𝑇 0 𝑇 𝑥(𝑡) 𝑥(𝑡 + 𝜏)d𝑡 对于平稳随机信号,上式变为: 𝑅𝑥(𝜏) = 𝑙𝑖𝑚 𝑇→∞ 1 𝑇 0 𝑇 𝑥(𝑡) 𝑥(𝑡 + 𝜏)𝑝(𝑥)d𝑡

SMEE 机械与电气工程学院 School of Machanical and Elcetrical Engineering 2.连续信号x(t)采样所得的离散信号的自相关函数,其中△t为采样时间, r是时间滞后量级,r=0,1,2..m: n-r Rr·△t)= 1 n-rL Xk Xk+r k=1 机城与电气工程学院
机械与电气工程学院 School of Machanical and Elcetrical Engineering 2. 连续信号𝑥(𝑡)采样所得的离散信号的自相关函数,其中Δ𝑡为采样时间, 𝑟是时间滞后量级,𝑟 = 0,1,2 … m : 𝑅𝑥(𝑟 ⋅ Δ𝑡) = 1 𝑛 − 𝑟 𝑘=1 𝑛−𝑟 𝑥𝑘 𝑥𝑘+𝑟