
第三章线性分类器 966 确定分类的关键技术之一是确定判别函数 例:贝叶斯决策,实际是用后验概率密度P(w:/x) 作为判别函数。但P(w:/x)估计有困难(p(x/W;)难 确定)。 另一种方法:直接用样本集设计分类器
确定分类的关键技术之一是确定判别函数 例:贝叶斯决策,实际是用后验概率密度P(wi/x) 作为判别函数。但P(wi/x)估计有困难(p(x/wi)难 确定)。 另一种方法:直接用样本集设计分类器。 第三章 线性分类器
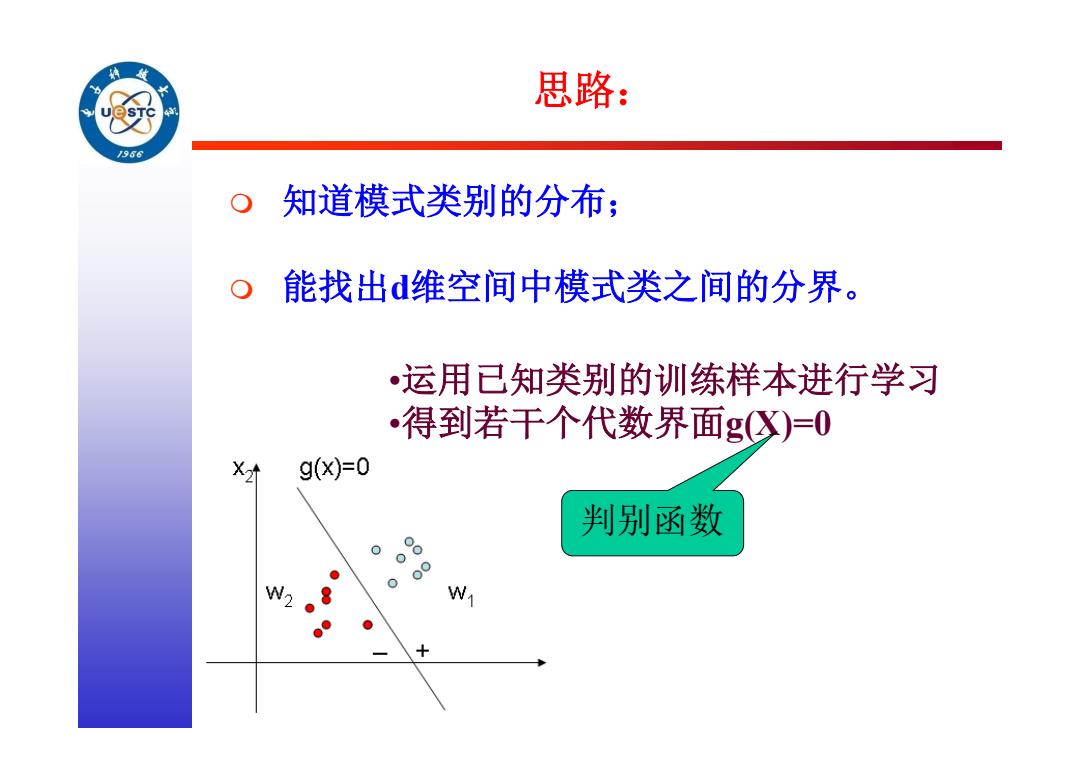
思路: /96 知道模式类别的分布; 能找出d维空间中模式类之间的分界。 运用已知类别的训练样本进行学习 得到若干个代数界面g心)=0 9(X)=0 判别函数 08 W2 0o0 N 00
思路: 知道模式类别的分布; 能找出d维空间中模式类之间的分界。 •运用已知类别的训练样本进行学习 •得到若干个代数界面g(X)=0 判别函数

966 两个步骤: 1)确定判别函数类型g:(x) 2)利用样本集确定判别函数的未知参数
两个步骤: 1)确定判别函数类型gi(x) 2)利用样本集确定判别函数的未知参数

线性判别函数 J966 线性判别函数: 当g(x)只是样本x的一次函数时,称为线性 判别函数,对应的分界面为超平面。 或:对于c个类别,各给出一个由d个特征组成的 单值函数,叫做线性判别函数。 记为g1(x),,g。(x),分别对应w1,,W
线性判别函数 线性判别函数: 当g(x)只是样本x的一次函数时,称为线性 判别函数,对应的分界面为超平面。 或:对于c个类别,各给出一个由d个特征组成的 单值函数,叫做线性判别函数。 记为g1(x),…,gc(x),分别对应w1,…,wc

966 若g()>g(),ij,j=1,,C,则k∈w 在w与w,的分界面上,则g)=g) 数学表达式: g(x)=w'x+wo 其中: w一d维权向量w=[w,w2,…,wa] X一d维特征向量x=[x,x2,…,xa] w。一阈值权
若 gi (x)>gj (x),ij,j=1,…,c,则xwi ; 在wi 与wj 的分界面上,则gi (x)=gj (x) 数学表达式: 0 ( ) T g x w x w w —d维权向量 x —d维特征向量 w0 —阈值权 1 2 [ , , , ]T w w w w d 1 2 [ , , , ]T d x x x x 其中:

966 两类问题:判别函数可采用 8(x)=81(x)-82(x) 若g(x)>0,则决策x∈w1 g(x)<0,则决策x∈Ww2 g(x)=0,则拒判或决策为任何一类 两类别的分界面: g(x)=0 d维线性平面,称为超平面, 也称决策面H
两类问题: 1 2 g x g x g x ( ) ( ) ( ) 若 , 则决策xw1 g x( ) 0 g x( ) 0 , 则决策xw2 g x( ) 0 , 则拒判或决策为任何一类 两类别的分界面: 判别函数可采用 ——d维线性平面,称为超平面, 也称决策面H g(x)=0

J966 当正1时,判别边界为分界点 当正2时,判别边界为一直线 当止3时,判别边界为一平面 当dD3时,判别边界为一超平面
当d=2时,判别边界为一直线 当d=1时,判别边界为分界点 当d=3时,判别边界为一平面 当d>3时,判别边界为一超平面

966 决策界面H的性质: 1)决策面H与权向量W的关系:W与正交 设两个向量x,x,都在决策面上,即 x,x2∈H 则有: wX1+w=wx2+w。→w(x-x2)=0 x,x2为决策面上任意两点,'.x1-X2是H面上的 任意向量
1) 决策面H与权向量W的关系:W与H正交 设两个向量 x x 1 2 , 都在决策面上,即 1 2 x x H , 1 0 2 0 1 2 ( ) 0 T T T w x w w x w w x x ∵ 为决策面上任意两点,∴ 是H面上的 任意向量 1 2 x x, 1 2 x x 则有 : 决策界面H 的性质:
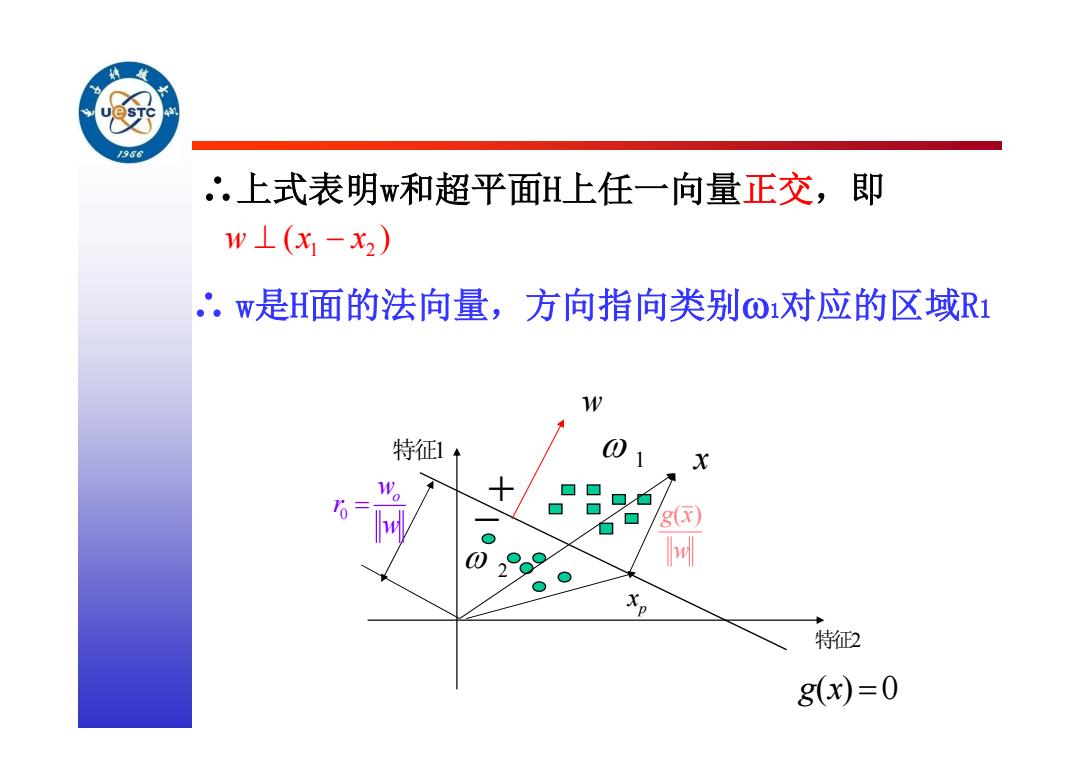
/96 '.上式表明w和超平面H上任一向量正交,即 w⊥(x-x2) '。w是H面的法向量,方向指向类别O1对应的区域R1 W 特征1+ X 8 2o9 Xp 特征2 8(x)=0
∴上式表明w和超平面H上任一向量正交,即 1 2 w x x ( ) ∴ w是H面的法向量,方向指向类别1对应的区域R1 g x( ) w 2 1 特征1 特征2 g x( ) 0 w x p x 0 wo r w
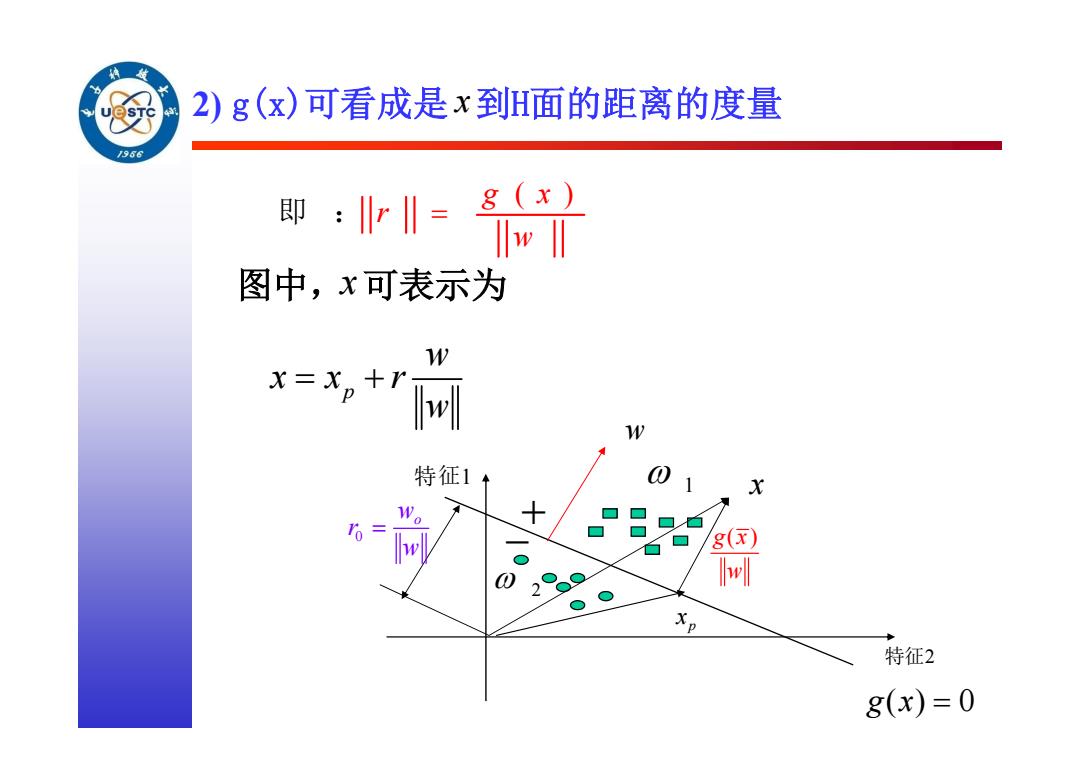
2)g(x)可看成是x到H面的距离的度量 966 即:业= 8(x) 图中,x可表示为 x=xp+r w 特征1 X + 8(x) w 特征2 8(x)=0
2) g(x)可看成是 x到H面的距离的度量 图中,x可表示为 p w x x r w ( ) 即 : g x r w g x( ) w 2 1 特征1 特征2 g x( ) 0 w x p x 0 wo r w