
第五章近邻法 /96 是一种分段线性分类器 直接根据训练样本对新样本进行分类
是一种分段线性分类器 直接根据训练样本对新样本进行分类 第五章 近邻法

距离度量 /96 度量D(:,)本质上是一个函数,该函数给出了两个模式之间的标量 距离的大小。一个度量必须满足4个性质: 对于任意的向量a,b,和c,有 o非负性:D(a,b)≥0 自反性:D(a,b)=0当且仅当a=b 对称性:D(a,b)=D(b,a) a三角不等式D(a,b)+D(b,c)≥D(a,c)
距离度量 度量D(· , ·)本质上是一个函数,该函数给出了两个模式之间的标量 距离的大小。一个度量必须满足4个性质: 对于任意的向量a,b,和c,有 非负性:D(a,b) ≥0 自反性:D(a,b)=0 当且仅当 a=b 对称性:D(a,b)=D(b,a) 三角不等式D(a,b)+D(b,c) ≥ D(a,c)

距离度量 966 d维空间中的欧式距离 abN-2a-r 能够满足这些性质
距离度量 d维空间中的欧式距离 能够满足这些性质 ( , ) ( ) 1/2 d 2 k k k 1 D a b a b

距离度量 966 更为一般的d维空间的度量为Minkowski距离度量 4ab-[②a-hrj 通常也被称为L范数 欧式距离就是L,范数
距离度量 更为一般的d维空间的度量为Minkowski距离度量 通常也被称为Lk范数 欧式距离就是L2范数 / ( , ) | | 1 k d k k i i i 1 L a b a b

距离度量 966 L,范数 L/a,b)=>la-bl i三 也被称为Manhattan距离或街区距离、绝对距离 显然,欧式距离和绝对距离是明氏距离的两个特例 手工运算时,为简便起见,通常采用绝对距离
距离度量 L1范数 也被称为Manhattan距离或街区距离、绝对距离 显然,欧式距离和绝对距离是明氏距离的两个特例 手工运算时,为简便起见,通常采用绝对距离 ( , ) | | d 1 i i i 1 L a b a b

最近邻法 966 1.最近邻法规则 已知C类,每类样本数为N个,i=1,2,.C 判别函数:8,(x)=minx-x‖k=1,2,N 决策规则:8,(x)=min8,(x)i=1,2,c 则决策x∈w —称为最近邻法
最近邻法 ( ) min 1, 2,..., k i i i g x x x k N ( ) min ( ) 1, 2,... j i i g x g x i c j x w ——称为最近邻法 1.最近邻法规则 判别函数: 决策规则: 已知C类,每类样本数为Ni个, i c 1,2,... 则决策

J966 最近邻法实质: 就是将样本x与N个已知类别属性的样本之间的 欧氏距离进行比较,将x归入最近的样本所属的类 别。 最近邻法是次优方法,误差率比贝叶斯误差率 大,当N→o,误差率不超过贝叶斯误差率2倍。 但不具有统计特性,不稳定
最近邻法实质: 就是将样本x与N个已知类别属性的样本之间的 欧氏距离进行比较,将x归入最近的样本所属的类 别。 最近邻法是次优方法,误差率比贝叶斯误差率 大,当N,误差率不超过贝叶斯误差率2倍。 但不具有统计特性,不稳定

/96 >在样本数很大时,最近邻规则能很好的工作 样本数非常大时,认为x距离x足够近,使 P(w;/x)=P(w;/x) ,'。最近邻规则是真实概率的一个有效近似 相当于决策规则为: P(w,x)=max P(w;x) X∈W;
在样本数N很大时,最近邻规则能很好的工作 ( / ') ( / ) P w x P w x i i ( | ) max ( | ) i j i j P w x P w x x w ∴ 最近邻规则是真实概率的一个有效近似 ∵样本数非常大时,认为x距离x足够近,使 相当于决策规则为:

/96 最近邻规则相当于把特征空间分成一个个网格单 元,每一个单元的点到最近邻x'(代表点)的距 离比到其它样本点距离更近 ,'.小单元中的任意点的类别就与最近邻x的类别 相同。即x与N个训练样本比较欧氏距离,x归入最 近样本的类
最近邻规则相当于把特征空间分成一个个网格单 元,每一个单元的点到最近邻x(代表点)的距 离比到其它样本点距离更近 ∴小单元中的任意点的类别就与最近邻x的类别 相同。即x与N个训练样本比较欧氏距离,x归入最 近样本的类
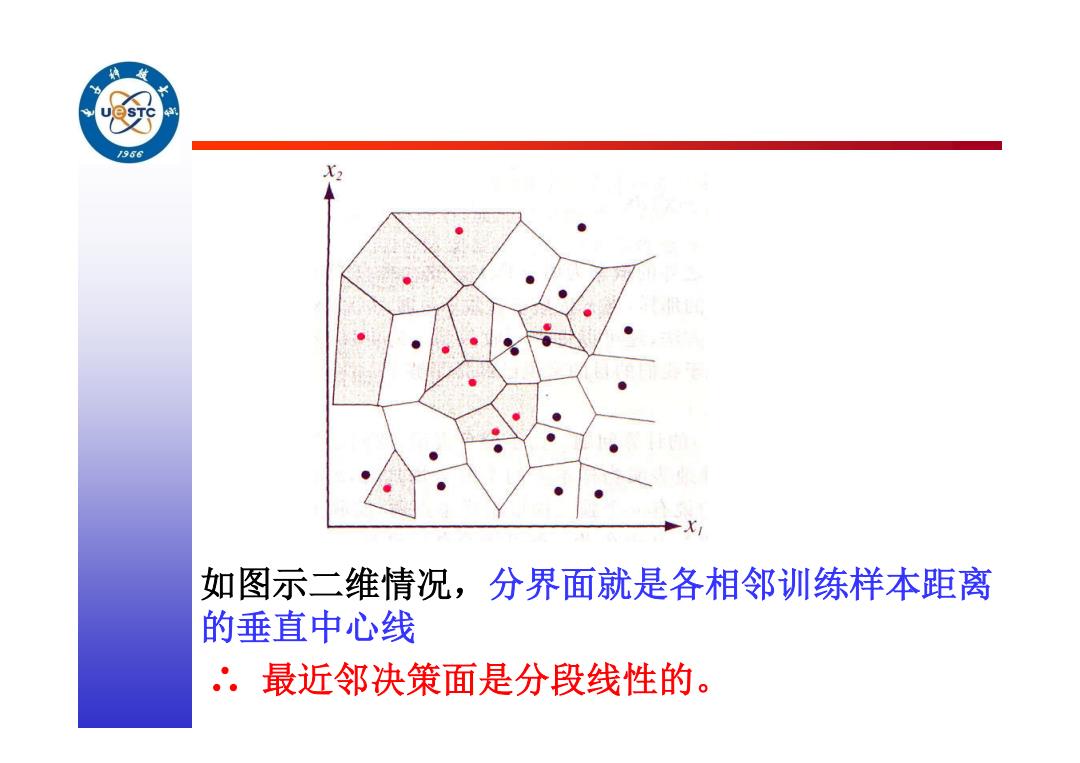
/956 X2 如图示二维情况,分界面就是各相邻训练样本距离 的垂直中心线 ∴.最近邻决策面是分段线性的
∴ 最近邻决策面是分段线性的。 如图示二维情况,分界面就是各相邻训练样本距离 的垂直中心线