
SMEE 机械与电气工程学院 School of Machanical and Elcetrical Engineering 第七章时间序列分析 一、 时间序列的定义 二、时序的时域特征值 三、时序的相关分析 四、时序的功率谱分析 机越与电气工程学院
机械与电气工程学院 School of Machanical and Elcetrical Engineering 第七章 时间序列分析 一、时间序列的定义 二、时序的时域特征值 三、时序的相关分析 四、时序的功率谱分析

SME 机械与电气工程学院 School of Machanical and Elcetrical Engineering 一、时间序列的定义 通常的机械过程都是平稳随机过程,在动态测试中测试信号往往是 时间的函数。 即传感器拾取连续变化的信号,经A/D转换得到的离散数据序列: {xk},k=1,2,,N(N为测量样本数)→称为一个时间序列 ② 每个时序数据都是该平稳随机过程中无限多个样本函数当中的一个, 而各态历经告诉我们,可以用一个或少数几个时间序列(或样本)来描述 这个随机过程(机械过程) ③ 时序分析是为了根据已有的历史数据对未来进行预测。为了分析时间 序列的数学特征,需要建立时序模型。 机越与电气工程学院
机械与电气工程学院 School of Machanical and Elcetrical Engineering ① 通常的机械过程都是平稳随机过程,在动态测试中测试信号往往是 时间的函数。 即传感器拾取连续变化的信号,经 A / D 转换得到的离散数据序列: 𝑥𝑘 , 𝑘 = 1, 2, … ,N (N 为测量样本数) ⇒ 称为一个时间序列 ② 每个时序数据都是该平稳随机过程中无限多个样本函数当中的一个, 而各态历经告诉我们,可以用一个或少数几个时间序列(或样本)来描述 这个随机过程(机械过程)。 ③ 时序分析是为了根据已有的历史数据对未来进行预测。为了分析时间 序列的数学特征,需要建立时序模型。 一、时间序列的定义

机械与电气工程学院 School of Machanical and Elcetrical Engineering 二、时序的时域特征值 均值: x(t)dt(定义式) → lim Xk N→0 N T→0,N→0 均方值: Aix=ux N 醒-引0a(定义式 1 0→ lim 脱=好 N-o∞N 其中,x、?都是真实均值、均方值的无偏估计, 存在方差V(x)、V(好)跟时间、信号特性有关。 机械与电气工程学院
机械与电气工程学院 School of Machanical and Elcetrical Engineering 均值: 𝜇 𝑥 = 1 𝑇 0 T 𝑥 𝑡 𝑑𝑡 (定义式) → 𝑙𝑖𝑚 𝑁→∞ 1 𝑁 𝑘=1 𝑁 𝑥𝑘 均方值: 𝜓 𝑥 2 = 1 𝑇 0 𝑇 𝑥 2 𝑡 𝑑𝑡 (定义式) → 𝑙𝑖𝑚 𝑁→∞ 1 𝑁 𝑘=1 𝑁 𝑥𝑘 2 𝑇 → ∞, 𝑁 → ∞ 𝜇 𝑥 = 𝜇𝑥 𝜓 𝑥 2 = 𝜓𝑥 2 二、时序的时域特征值 其中,𝜇 𝑥、𝜓 𝑥 2都是真实均值、均方值的无偏估计, 存在方差V(𝜇 𝑥)、 V(𝜓 𝑥 2)跟时间、信号特性有关

SMEE 机械与电气工程学院 School of Machanical and Elcetrical Engineering 三、时序的相关分析 自相关一 该随机过程的线性相关程度,即平稳性、变化剧烈/缓慢? 互相关一 两个随机过程的相似程度 (一)自相关 Rx(t)=x(t)x(t-t)dt (定义式) 存在估计真实Rx()的方差V[Rx()] 机越与电工程学院
机械与电气工程学院 School of Machanical and Elcetrical Engineering (一)自相关 𝑅 𝑥 𝜏 = 1 𝑇 0 𝑇 𝑥 𝑡 𝑥 𝑡 − 𝜏 𝑑𝑡 (定义式) 存在估计真实 𝑅𝑥 𝜏 的方差 𝑉[𝑅 𝑥(𝜏)] 三、时序的相关分析 自相关 —— 该随机过程的线性相关程度,即平稳性、变化剧烈 / 缓慢? 互相关 —— 两个随机过程的相似程度

SMEE 机械与电气工程学院 School of Machanical and Elcetrical Engineering 获取自相关函数()的途径: ①模拟分析 自相关分析仪(属于信号的连续估计) ② 数字分析一借用计算机的离散处理 x(t)FT功率谱Sx(ω)FT-1Rx(t) (维纳-辛钦公式) 或:R,=R(rA)=己,∑餐ixxk-r (实用公式) r一时间滞后量级,r=0,1,2…,几 ,是真实Rx(x)在r△t处的估计,改变r可得自相关图 {xk}是均值为0的各态历经时序序列 机越与电气工程学院
机械与电气工程学院 School of Machanical and Elcetrical Engineering 𝑥 𝑡 𝐹𝑇 功率谱 𝑆𝑥 𝜔 𝐹𝑇 −1 𝑅𝑥 𝜏 (维纳-辛钦公式) 或:𝑅 𝑟 = 𝑅 𝑥 𝑟𝛥𝑡 = 1 𝑛−𝑟 𝑘=1 𝑛−𝑟 𝑥𝑘𝑥𝑘 −𝑟 (实用公式) 𝑟 — 时间滞后量级,𝑟 = 0, 1, 2 … , 𝑛 𝑅 𝑟 是真实 𝑅𝑥 𝜏 在 𝑟Δ𝑡 处的估计,改变 𝑟 可得自相关图 𝑥𝑘 是均值为 0 的各态历经时序序列 获取自相关函数 𝑅 𝑥 𝜏 的途径: ① 模拟分析 —— 自相关分析仪(属于信号的连续估计) ② 数字分析 —— 借用计算机的离散处理

SMEE 机械与电气工程学院 School of Machanical and Elcetrical Engineering 时间序列自相关函数的重要性质: ① R0=Rx(0)=∑k=1(xk)2=经 (初始相关即为样本均方值) 且:max[Rx(t)]=R。 ② 自相关系数 =() Rx(t) 其中x=r△t 了1,T=0 对于正态信号:Px= 0,T≠0 机越与电气工程学院
机械与电气工程学院 School of Machanical and Elcetrical Engineering ① 𝑅 0 = 𝑅 𝑥 0 = 1 𝑛 𝑘=1 𝑛 𝑥𝑘 2 = 𝜓 𝑥 2 (初始相关即为样本均方值) 且:max 𝑅 𝑥 𝜏 = 𝑅 𝑜 ② 自相关系数 𝜌 𝑥 = 𝑅 𝑥 𝜏 𝑅 𝑥(𝑜) = 𝑅 𝑟 𝑅 𝑜 , 其中 𝜏 = 𝑟Δ𝑡 对于正态信号:𝜌𝑥 = 1, 𝑟 = 0 0, 𝑟 ≠ 0 时间序列自相关函数的重要性质:
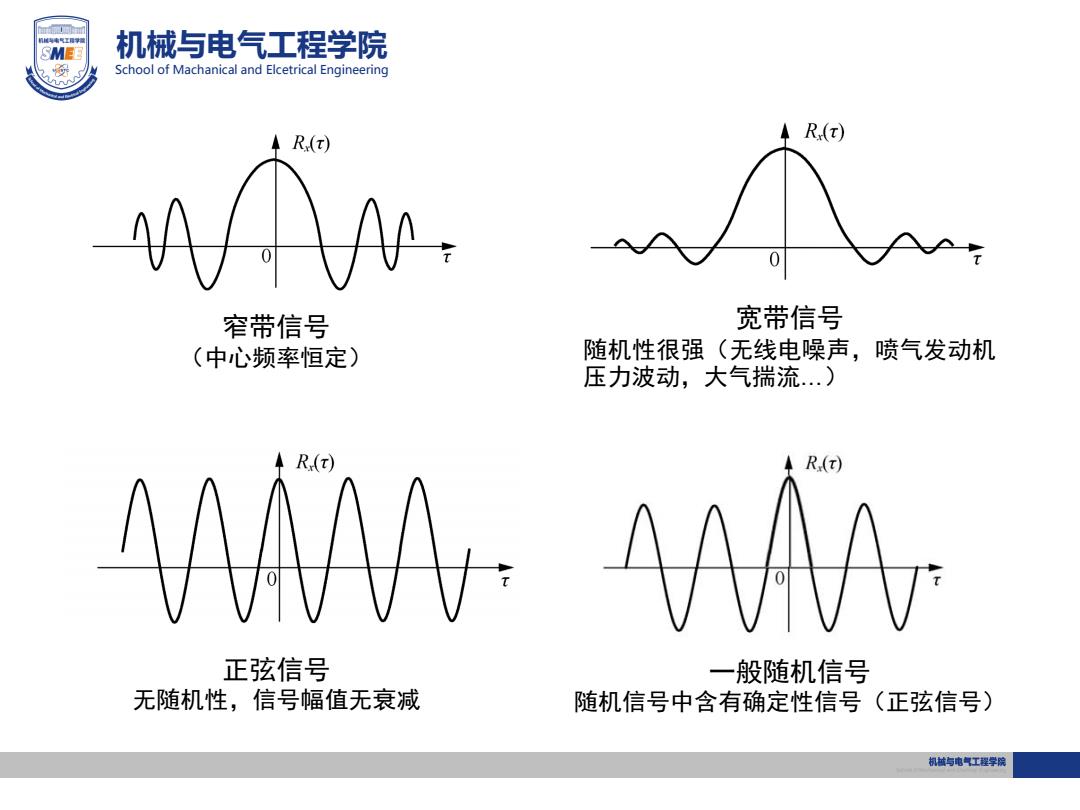
SMEE 机械与电气工程学院 School of Machanical and Elcetrical Engineering 4R(t) R() 窄带信号 宽带信号 (中心频率恒定) 随机性很强(无线电噪声,喷气发动机 压力波动,大气揣流.) R() 时女4讲切 R(T 正弦信号 一般随机信号 无随机性,信号幅值无衰减 随机信号中含有确定性信号(正弦信号) 机越与电气工程学院
机械与电气工程学院 School of Machanical and Elcetrical Engineering 窄带信号 (中心频率恒定) 宽带信号 随机性很强(无线电噪声,喷气发动机 压力波动,大气揣流…) 正弦信号 无随机性,信号幅值无衰减 一般随机信号 随机信号中含有确定性信号(正弦信号)
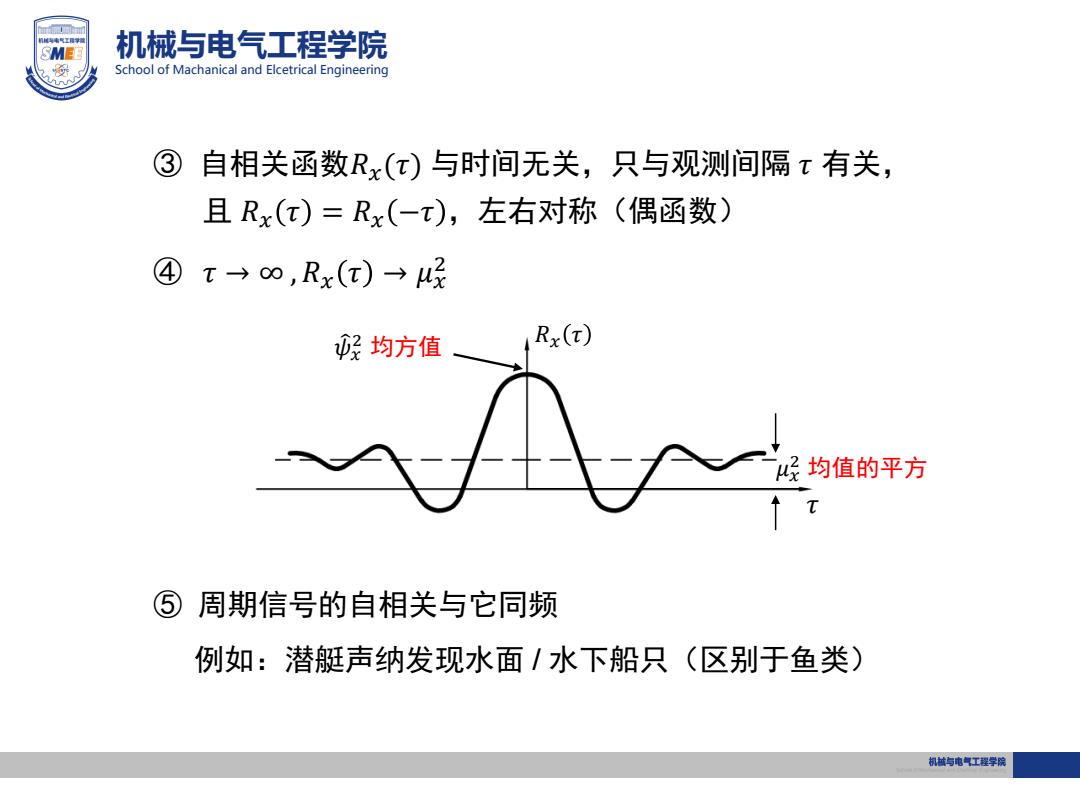
SMEE 机械与电气工程学院 School of Machanical and Elcetrical Engineering ③ 自相关函数Rx()与时间无关,只与观测间隔x有关, 且Rx()=Rx(-T),左右对称(偶函数) ④T→∞,Rx(t)→ 好均方值 Rx(t) ?均值的平方 ⑤周期信号的自相关与它同频 例如:潜艇声纳发现水面/水下船只(区别于鱼类) 机越与电气工程学院
机械与电气工程学院 School of Machanical and Elcetrical Engineering ③ 自相关函数𝑅𝑥(𝜏) 与时间无关,只与观测间隔 𝜏 有关, 且 𝑅𝑥 𝜏 = 𝑅𝑥 −𝜏 ,左右对称(偶函数) ④ 𝜏 → ∞ , 𝑅𝑥 𝜏 → 𝜇𝑥 2 𝑅𝑥 𝜏 𝜏 𝜓 𝑥 2 均方值 𝜇𝑥 2 均值的平方 ⑤ 周期信号的自相关与它同频 例如:潜艇声纳发现水面 / 水下船只(区别于鱼类)

SMEE 机械与电气工程学院 School of Machanical and Elcetrical Engineering (2)互相关 Rxy(r)=()y(+dt=lim Rxy (r) 且Rxy(t)=Ryx(-t)(一般不是t的偶函数) 若分别对x(t)、y(t)按照时间间隔△t采样r=1,2,.N, 而单位延迟时间△x=△t,则x=nAt,t=rAt, 互相关函数为: Rxy(n)=E[x(r)y(r+m]=im是∑=x(r)y(+n)(实用公式) T→0oW 机越与电气工程学院
机械与电气工程学院 School of Machanical and Elcetrical Engineering (2) 互相关 𝑅𝑥𝑦 𝜏 = lim 𝑇→∞ 1 𝑇 0 𝑇 𝑥 𝑡 𝑦 𝑡 + 𝜏 𝑑𝑡 = lim 𝑇→∞ 𝑅 𝑥𝑦 𝜏 且 𝑅𝑥𝑦 𝜏 = 𝑅𝑦𝑥 −𝜏 (一般不是 𝜏 的偶函数) 若分别对𝑥 𝑡 、𝑦 𝑡 按照时间间隔Δ𝑡 采样𝑟 =1,2,….N, 而单位延迟时间Δ𝜏 = Δ𝑡,则𝜏 = 𝑛Δ𝑡,𝑡 = 𝑟Δ𝑡, 互相关函数为: 𝑅𝑥𝑦 𝑛 = 𝐸 𝑥 𝑟 𝑦 𝑟 + 𝑛 = lim 𝑇→∞ 1 𝑁 𝑟=1 𝑁−1 𝑥 𝑟 𝑦 𝑟 + 𝑛 (实用公式)

机械与电气工程学院 School of Machanical and Elcetrical Engineering [例题]悬臂梁的弯曲问题 悬臂梁上同时有两处动载荷F(t)和F2(t),分别产生端部挠度x(t) 和y(t),设端部总挠度为z(t),试用相关分析描述悬臂梁的弯曲问题。 F(0) 解:悬臂梁同时受动载荷F(t)和F2(t) 其端部总挠度为:z(t)=x(t)+y(t) (a) F2(t) (b) 机越与电气工程学院
机械与电气工程学院 School of Machanical and Elcetrical Engineering [例题] 悬臂梁的弯曲问题 悬臂梁上同时有两处动载荷 𝐹1 𝑡 和 𝐹2(𝑡) ,分别产生端部挠度 𝑥(𝑡) 和 𝑦 𝑡 , 设端部总挠度为 𝑧(𝑡) ,试用相关分析描述悬臂梁的弯曲问题。 解:悬臂梁同时受动载荷 𝐹1 𝑡 和 𝐹2 𝑡 其端部总挠度为:𝑧 𝑡 = 𝑥 𝑡 + 𝑦(𝑡)