
意义: 平均数是一组资料的代表值,表示资料中 观察值的中心位置与集中趋势。 种类: 主要有算术平均数(Average)、 中位数(Median)、 众数(Mode) 几何平均数(Geometric mean)
平均数是一组资料的代表值,表示资料中 观察值的中心位置 与集中趋势 。 意义: 种类: 主要有 算术平均数(Average)、 中位数(Median)、 众 数(Mode ) 几何平均数(Geometric mean )

算术平均数(x)的性质 (1) X的大小受样本内每个值的影响 (2)若每个X都乘以相同的数K,则x也应乘以K (3)若每个X都加上相同的数A,则x也应加上A。 (4)离均差之和等于零。 (5)离均差之平方和最小
(1) 的大小受样本内每个值的影响 的大小受样本内每个值的影响 (2)若每个Xi都乘以相同的数 都乘以相同的数K,则 也应乘以K (3)若每个Xi都加上相同的数 都加上相同的数A,则 x 也应加上A。 x x x 算术平均数( ) 的性质 (4)离均差之和等于零。 )离均差之和等于零。 (5)离均差之平方和最小。 )离均差之平方和最小

本次内容 标准差 变异系数 第二章概率分布 米 米
本次内容 标准差 第二章 概率分布 变异系数

度量数据的离散程度: 极差 平均离差 标准差 方差 变异系数 米
度量数据的离散程度: 极差 平均离差 标准差 方差 变异系数

常用的几种标志变异指标 概念 计算 特点 优点:容易理解, 1。极差 数列中最大值R=最大值最小值 计算方便 (R) 与最小值之差 缺点:不能反映全 部数据分布状况 2.平均离差 各观察值与 简单: 优点:反映全部 (A、D) 均值离差绝 4D= X-X 数据分布状况 对值的算术 n 加权: 缺点:取绝对 平均 AD-1 - 值 ,数字上 不尽合理
2.平均离差 (A、D) 概 念 计 算 特 点 数列中最大值 与最小值之差 1.极差 (R) R=最大值-最小值 优点:容易理解, 优点:容易理解, 计算方便 缺点:不能反映全 缺点:不能反映全 部数据分布状况 部数据分布状况 各观察值与 均值离差绝 对值的算术 平均 i i f fiXX DA n XX DA i 简单: 加权: 优点:反映全部 优点:反映全部 数据分布状况 缺点:取绝对 值 ,数字上 不尽合理

概念 计算 特点 各标志值与均 优点:反映全部 3.方差 值离差平方的 简单:口-砂 (S2) 平均。 数据分布状况 和 加权 d/ 缺点:受计量单 标准差 方差的平方根 位和平均水平影 (取正根) 响,不便于比较 (S, 4.变 标准差与均值 优点:适宜不同数 系数 S 之商,可以用 据的比较,是无量纲 来比较不同资 的系数 (CV) 料的相对变异 缺点:对数据结构 程度 变化反应不灵敏 方差(σ2)和标准差(。)是应用最广的标志变异指标
概 念 计 算 特 点 各标志值与均 值离差平方的 平均。 方差的平方根 (取正根) 3.方差 ( ,σ 2 ) 和 标准差 (S, σ ) 优点:反映全部 优点:反映全部 数据分布状况. 缺点:受计量单 位 和平均水平 影 响,不便于比较 响,不便于比较 4.变异 系数 (CV ) 标准差与均值 之商,可以用 来比较不同资 料的相对变异 程度 简单: 加权: 优点:适宜不同数 据的比较,是无量纲 的系数 缺点:对数据结构 变化反应不灵敏 f fXX 2 2 n i XX 2 2 2 方差( σ 2 )和标准差( σ )是应用最广的标志变异指标 是应用最广的标志变异指标 2 S x s cv
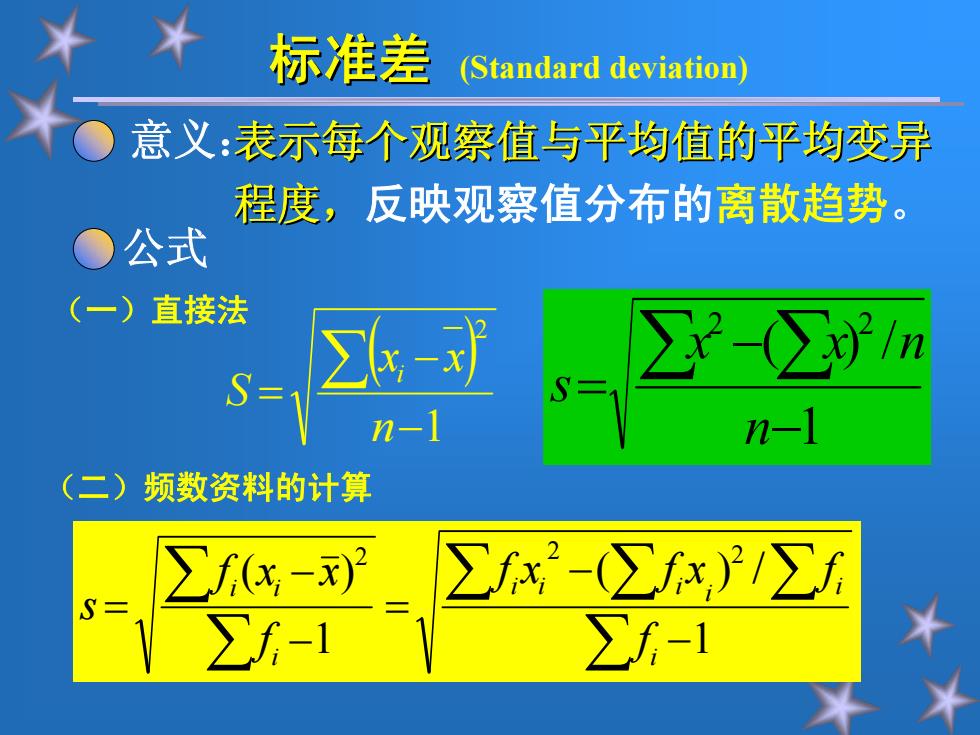
标准差 (Standard deviation) 意义:表示每个观察值与平均值的平均变异 程度,反映观察值分布的离散趋势。 公式 (一)直接法 ∑2n n- n-1 二) 频数资料的计算 ∑3- ∑x2-(∑f2∑f ∑-1 ∑f-1
意义:表示每个观察值与平均值的平均变异 表示每个观察值与平均值的平均变异 程度,反映观察值分布的离散趋势。 公式 1 2 n xx S i (一)直接法 (二)频数资料的计算 1 /)( 1 )( 2 2 2 i i i ii i i ii f fxfxf f xxf s 1 /)( 2 2 n nxx s 标准差 (Standard deviation)

例计算以下数据的标准差:26252824232527273021。 才
例 计算以下数据的标准差:26 25 28 24 23 25 27 27 30 21

解最好列成以下表格的形式计算 676 25 625 ∑x ∑x)2 28 784 24 576 23 529 s= n-1 25 625 27 729 27 729 =2.59 30 900 21 441 256 6614
26 676 25 625 28 784 24 576 23 529 25 625 27 729 27 729 30 900 21 441 256 6614 解 最好列成以下表格的形式计算 1 )( 2 2 n n x x s i i =2.59 2 x x x
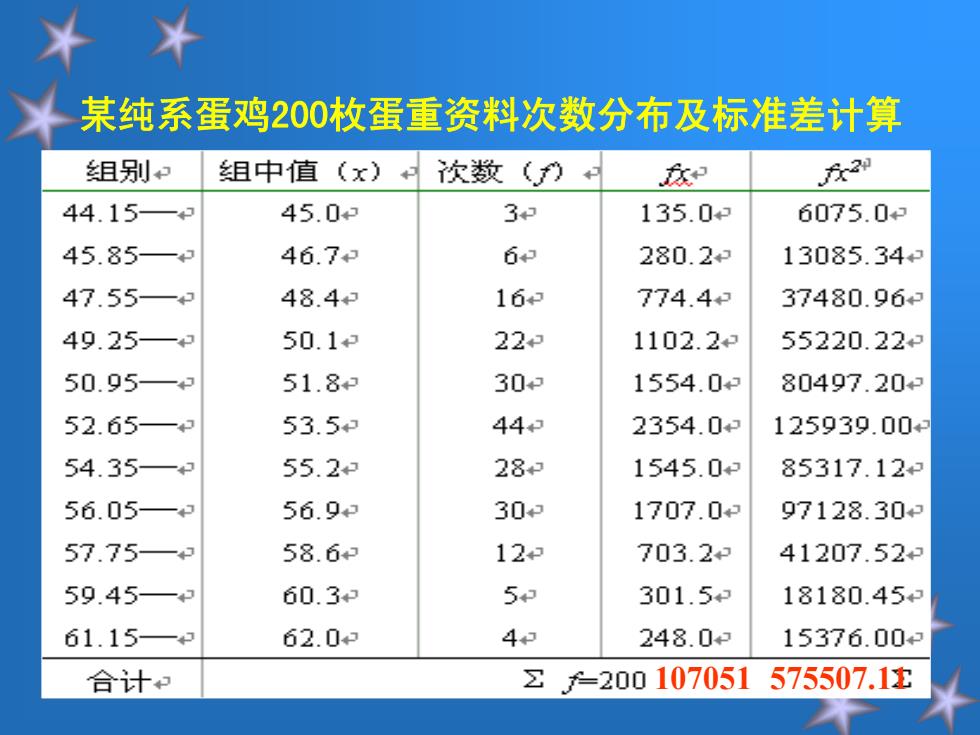
某纯系蛋鸡200枚蛋重资料次数分布及标准差计算 组别 组中值(x)次数() 和 r2刚 44.15—3 45.02 3 135.0 6075.02 45.85—3 46.7 62 280.2 13085.34 47.553 48.4 163 774.4 37480.963 49.25— 50.13 223 1102.2 55220.22 50.953 51.8 302 1554.03 80497.203 52.65— 53.5 44 2354.0 125939.00¥ 54.35— 55.23 28 1545.0 85317.12 56.05— 56.93 303 1707.0 97128.30 57.75—9 58.6 12p 703.29 41207.529 59.45—3 60.3 5 301.5 18180.45 61.15— 62.03 43 248.02 15376.00 合计和 Σ -200107051 575507.1
某纯系蛋鸡200枚蛋重资料次数分布及标准差计算 107051 575507.11