山东大学2013-2014学年2学期数字信号处理(双语)课程试卷()答案与评分细则 1.(10 pts,2 pts for each) (e)(5 pts)ROC: The ystm is stable.sie the ROC includes the un circle. 1)C;2)A;3)A4)B,5)D: (f)(7pts) -19- -63 44 2.(40 pts)Solution:H(=)=- 64--.30-126-+24:.y日 (e-2--3) 6-5+2 X() H(间=24+1-56-+W6=24+-5*-万 (a)(5 pts)poles:=1,Zp2=1/3;zeros:4,2=1/5;it isn't a minimum-phase system. The impulse response hin]is (b)(5 pts)The difference equation:6y[n]5y[n-1]+y[n-2]=30x[n]-126x[n-1]+24x[n-2]. n=246-63/2y°+443)}”m. ory[(56w[m-l]+1/6)y[m-2]=5x[间-21xn-1刂+4x[n-21 (c)(5pts)The 2nd-order direct form II signal flow graph is (g)(8 pts)Determine expressions for a minimum-phase system H(and an all-pass H(e) 5-211+4:2 x[m] yin] system()such that H)H(() 1-(56)-+(y6) 5/6 -21 H(e) 6(4-4-1--5).-20(e-4)1-) -2-3)(1-/21-3例 f21 -1/6 .--a0-月-%-H日H.日 (-20-3)0-4 -19-=1 -63 44 5ps)H(阳间-24+1-6-w6e24+-万*-万 He月)-= -2001-/4)1-5 1-2j1--j The signal flow graph of parallel-form structure (2nd order)is 24 (--4) x[n] -19 H,-两 n Coefficients distributed in each terms may be different. 56,1 3.(15 pts)Proof:If Td=1,the system function of the continuous-time Butterworth filter is -16 Ist order parallel-form structure is 0.70326 0.7032 Hc(s)= where A= 24 器 -63 m 12 The impulse response of the continuous-time Butterworth filter is 暴 ke(0=∑4e0 (4pts) 1 第1页共2页
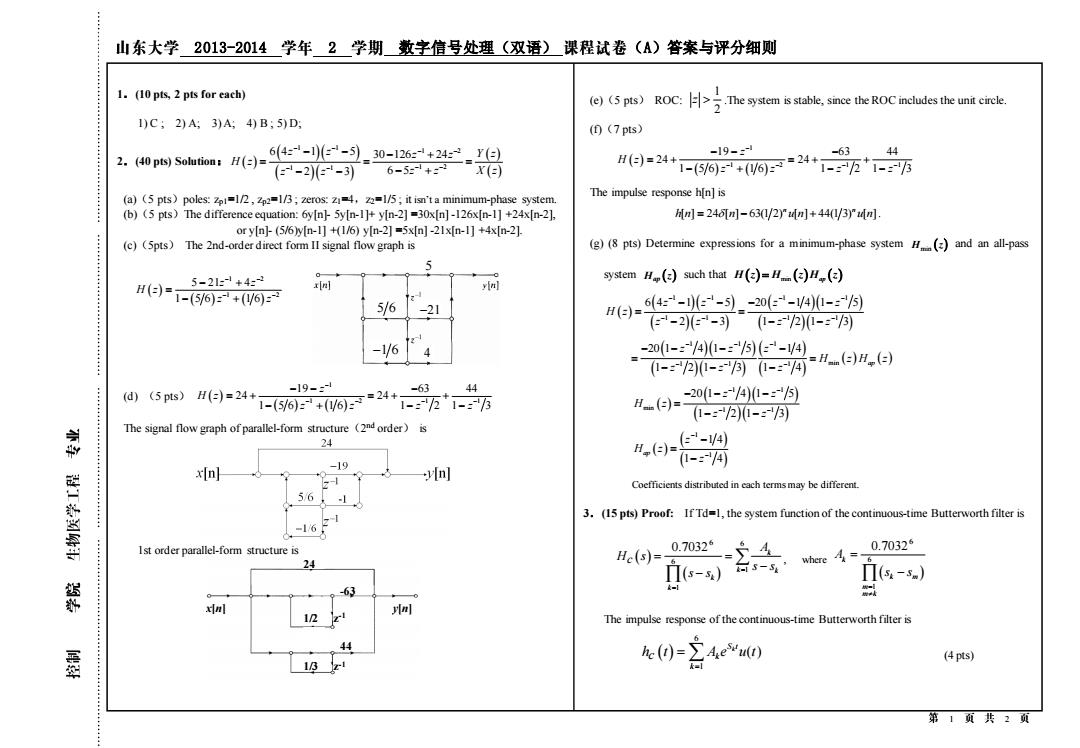
2013-2014 2 数字信号处理(双语) (A)答案与评分细则 1 2 1.(10 pts, 2 pts for each) 1) C ; 2) A; 3) A; 4) B ; 5) D; 2.(40 pts) Solution: ( ) ( )( ) ( )( ) ( ) ( ) 1 1 1 2 1 1 1 2 6 4 1 5 30 126 24 2 3 6 5 z z z z Y z H z z z z z X z − − − − − − − − − − − + = = = − − − + (a)(5 pts)poles: zp1=1/2 , zp2=1/3 ; zeros: z1=4,z2=1/5 ; it isn’t a minimum-phase system. (b)(5 pts)The difference equation: 6y[n]- 5y[n-1]+ y[n-2] =30x[n] -126x[n-1] +24x[n-2], or y[n]- (5/6)y[n-1] +(1/6) y[n-2] =5x[n] -21x[n-1] +4x[n-2]. (c)(5pts) The 2nd-order direct form II signal flow graph is ( ) ( ) ( ) 1 2 1 2 5 21 4 1 5 6 1 6 z z H z z z − − − − − + = − + (d) (5 pts) ( ) ( ) ( ) 1 1 2 1 1 19 63 44 24 24 1 5 6 1 6 1 2 1 3 z H z z z z z − − − − − − − − = + = + + − + − − The signal flow graph of parallel-form structure(2 nd order) is 1st order parallel-form structure is (e)(5 pts) ROC: 1 2 z .The system is stable, since the ROC includes the unit circle. (f)(7 pts) ( ) ( ) ( ) 1 1 2 1 1 19 63 44 24 24 1 5 6 1 6 1 2 1 3 z H z z z z z − − − − − − − − = + = + + − + − − The impulse response h[n] is [ ] 24 [ ] 63(1 2) [ ] 44(1 3) [ ] n n h n n u n u n = − + . (g) (8 pts) Determine expressions for a minimum-phase system H z min ( ) and an all-pass system ( ) H z ap such that ( ) min ( ) ( ) H z H z H z = ap ( ) ( )( ) ( )( ) ( )( ) ( )( ) 1 1 1 1 1 1 1 1 6 4 1 5 20 1 4 1 5 2 3 1 2 1 3 z z z z H z z z z z − − − − − − − − − − − − − = = − − − − ( )( ) ( )( ) ( ) ( ) ( ) ( ) 1 1 1 1 1 1 min 20 1 4 1 5 1 4 1 2 1 3 1 4 ap z z z H z H z z z z − − − − − − − − − − = = − − − ( ) ( )( ) ( )( ) 1 1 min 1 1 20 1 4 1 5 1 2 1 3 z z H z z z − − − − − − − = − − ( ) ( ) ( ) 1 1 1 4 1 4 ap z H z z − − − = − Coefficients distributed in each terms may be different. 3.(15 pts) Proof: If Td=1, the system function of the continuous-time Butterworth filter is ( ) ( ) 6 6 6 1 1 0.7032 k k k k k c A H s s s s s = = = = − − , where ( ) 6 6 1 0.7032 k k m m m k A s s = = − The impulse response of the continuous-time Butterworth filter is ( ) 6 1 ( ) k S t k k c h t A e u t = = (4 pts) 5 −16 −21 4 56 -63 44 1/3 1/2 24 z -1 z -1 x[n] y[n]

山东大学2013-2014学年2学期数字信号处理(双语)课程试卷()答案与评分细则 The impulse response of the discrete-time Butterworth filter is(when Td=1) 5.(10 pts)Solution: =A)=A间-宫4 (2pts) From the figure,the two 8-point sequences are related through a circular shift,ie.. [网=[a-4功,] (3 pts) If Td,the system function of the continuous-time Butterworth filter is From property 5 in Table 8.2, Hc(s)=- 070322-4匹 0.70326 s-/万, where DFT{s[n-4),]}=x[个 (3 pts) 6-) Thus, x=xk=e*x=(-旷x (4 pts) The impulse response of the continuous-time Butterworth filter(when Td)is -2*刚 6.(10 pts)Solution: (5pts) The array D[r]can be expressed in terms ofC[r]: The impulse response of the discrete-time Butterworth filter(when Td)is D[o=Co+C[4:D[刊=C刊+c[D[2=C[2+Wc[D[]=C[]+c[小: 阿Am)小宫手-宫44l (3pts) D[4-C0-C4:D[=C[-wc[:D[=CI2-mc:D[]=C[-wc[7]: Sothe impulse response of the discrete-time Butterworth filter with Td is the same as (4 pts) the result for Td=l,and the discrete-time filter system function H(z)are the same for both Solving the equations above for C[r]gives situations. (1 pts) C[o=C[p=c[2=c[3-1;C4=C[=c[6=C[7]=0. 4.(15 pts)Proof:Since]] (4 pts) For r=0,1.....7,a sketch of the sequence C[r]is provided below. 营闲财茗内 (3 pts) 2}时 (4 pts) 56 (2pts) 茶 =2片2 (4 pts) -a-叫 (4pts) 第2项共2页
2013-2014 2 数字信号处理(双语) (A)答案与评分细则 2 2 The impulse response of the discrete-time Butterworth filter is (when Td=1) ( ) ( ) 6 1 [ ] k S n d c d c k k h n T h nT h n A e u n = = = = (2 pts) If Td≠1, the system function of the continuous-time Butterworth filter is ( ) ( ) ( ) 6 6 6 1 1 0.7032 d k d k k d k d k c T A T H s s s T s s T = = = = − − , where ( ) 6 6 1 0.7032 k k m m m k A s s = = − The impulse response of the continuous-time Butterworth filter (when Td≠1 ) is ( ) 6 1 ( ) Sk Td t k d k A c T h t e u t = = (5 pts) The impulse response of the discrete-time Butterworth filter (when Td≠1 ) is ( ) 6 6 1 1 [ ] [ ] d k Sk Td nT S n d c d d k k k d k A T h n T h nT T e u n A e u n = = = = = (3 pts) So the impulse response of the discrete-time Butterworth filter with Td≠1 is the same as the result for Td=1, and the discrete-time filter system function H (z) are the same for both situations. (1 pts) 4.(15 pts) Proof: Since X k X k X k 3 1 2 = 1 3 3 0 1 N kn N k x n X k W N − − = = 1 1 2 0 1 N kn N k X k X k W N − − = = (3 pts) 1 1 1 2 0 0 1 N N km kn N N k m x m W X k W N − − − = = = (4 pts) ( ) 1 1 1 2 0 0 1 N N k n m N m k x m X k W N − − − − = = = (4 pts) 1 1 2 0 N m x m x n m − = = − (4 pts) 5.(10 pts) Solution: From the figure, the two 8-point sequences are related through a circular shift, i.e., 2 1 (( ))8 x n x n = − 4 (3 pts) From property 5 in Table 8.2, (( )) 4 1 8 1 8 4 k DFT x n W X k − = (3 pts) Thus, ( ) 4 2 8 1 1 1 1 k k j k X k W X k e X k X k − = = = − (4 pts) 6.(10 pts) Solution: The array D[r] can be expressed in terms of C[r]: D C C 0 0 4 = + ; 1 8 D C W C 1 1 5 = + ; 2 8 D C W C 2 2 6 = + ; 3 8 D C W C 3 3 7 = + ; D C C 4 0 4 = − ; 1 8 D C W C 5 1 5 = − ; 2 8 D C W C 6 2 6 = − ; 3 8 D C W C 7 3 7 = − ; (4 pts) Solving the equations above for C[r] gives C C C C 0 1 2 3 1 = = = = ; C C C C 4 5 6 7 0 = = = = . (4 pts) For r=0, 1, ... ,7, a sketch of the sequence C[r] is provided below. (2 pts)